一种改进的协同过滤推荐算法

李瑶

（天津大学数学学院，天津300350）

随着社会的发展，高度信息化，推荐系统已经成为了一个很重要的研究领域，是一个预测用户兴趣的模型.平时生活中推荐系统有很多应用，比如电子商务网站可以利用推荐系统向用户推荐可能想买的物品，视频电影网站可以向用户推荐其可能感兴趣的电影视频等[1].推荐算法其中有协同过滤、矩阵分解等等，矩阵分解基于评分矩阵来进行处理，为此在基于用户的协同过滤模型基础上，引进SVD分解后的svdprediction矩阵作为user-item-matrix应用于协同过滤模型，比单独的SVD优化快速且简便.所以本文在协同过滤算法的基础上，引入奇异值分解优化特征，利用SVD分解后SVD-prediction矩阵作为user-item-matrix应用于协同过滤模型进一步利用模型，来提高准确性.

而且考虑到用户不一定会评分，因为麻烦或其他因素，所以后期会对item本身所属的类别赋以较大的权重，最后使模型更贴合实际生活.

1 协同过滤算法

协同过滤（Collaboration Filtering）算法[2]是推荐系统中最常用的一种算法，本文采用的是依据相似用户的爱好对活动用户进行推荐的思想，也被称为基于用户的协同过滤，其中如果根据用户的评分数据寻找到与其相似的用户，并以此借助相似用户的爱好对其余用户进行推荐的思想被称为基于用户的协同过滤.本质上是寻找数据集中的相似用户来完成推荐[3]，其原理类似于朋友推荐，简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息，通过信息程度的回应（如评分），记录下来以达到过滤的目的进而帮助别人筛选信息[3-4]，比如通过对用户喜欢的item进行分析，发现用户A和用户B很相似，用户B喜欢了某个item，而用户A没有评价，那么就可以把这个item推荐给用户A.依据用户对物品的评分建立用户评分矩阵（协同过滤需要使用到的用户评价信息会被存储在一个数据表中，该表可以被称为用户评分矩阵），矩阵的行数为系统中用户的数量，列数为系统中物品的数量，没有评分数据的默认为零；然后依据用户评分矩阵计算相似度，用偏好等来进行运算[5].

整体流程构建如下：

1）收集用户评分信息

首先下载需要的数据，进行预处理，例如电影的编号重新映射到从1开始，会便于后续的评分矩阵处理.

2）定于相似度指标并计算

欧式距离分数计算，提取搜寻用户都评价过的电影的评分。

If：无共同评分的电影（Score=0）

Else：计算（rate1-rate2）的平方和的平方根皮尔逊系数（Pearson Correlation Coefficient）.

同样提取搜寻用户都评价过的电影的评分，然后计算，其中计算公式

COV（X，Y）表示X，Y的协方差，构建useritemmatrix作为特征输入，最后计算RMSE.

3）得出相似用户和推荐列表

按照得分进行排序，把得分降序排列，可以得到k个相似用户，本文设置的k为5，k可以按照需求来选取，然后去掉本身用户评分过的电影，其余为推荐条目.

2 SVD分解

SVD分解（Singularly Valuable Decomposition）也为奇异值分解，奇异值是矩阵里的概念，一般通过奇异值分解定理求得.

奇异值分解定理：一个向量v是方阵A的特征向量，可以表示成下面的形式：Av=kv，这时候k被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量.特征值分解是将一个矩阵分解成以下形式：A=USU-1，U是这个矩阵a的特征向量组成的矩阵，S是一个对角阵，每个对角线上的元素就是一个特征值.

设a为（m×n）阶矩阵，记为Am×n，如若m≠n时，不能直接按照上面的来计算，此时令q=min（m，n）.A×AT的q个非负特征值的算术平方根叫作A矩阵的奇异值.

对于一个实矩阵Am×n，如果可以分解为A=USVT，其中，U为（m×m）的正交阵，V为（n×n）的正交阵，S为（m×n）阶矩阵.记S的前r×r阶为S*，它为半正定对角矩阵，简写为

其中的a1，a2，…，ar称为矩阵A的奇异值.对于实际的运用A=USVT.举一个实际例子A6×3，来进行直观说明

个矩阵U，S，如下

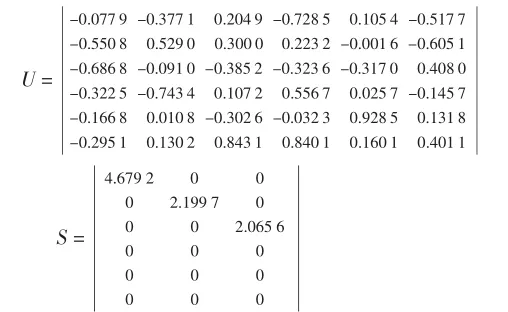
其中S=diag（4.679 2，2.199 7，2.065 6）.

后期维度增多后，本文会对SVD进行改进为HOSVD，简单介绍一下最简单的矩阵展开，例如将一个N维张量展开成为一个矩阵，按照不同的维度重新排列成一个矩阵，例如一个2×3×3的张量可以被展开为3×6或者2×9的矩阵.就是将张量按照不同的维度重新排列成一个矩阵，将这一过程称作张量的n—模矩阵展开，暂时不做过多说明.

3 数据与方法

分别在一组自行构建的数据上进行模拟训练，进行说明，后面在MovieLens数据集基础上，再选取一小部分不完全数据，进行验证（可以用在网站初期，或者新用户信息很少的情况下，在不完善的信息下，对几个算法进行比较评估，可以把大数据应用到比较好的算法模型上，得到推广），见表1.

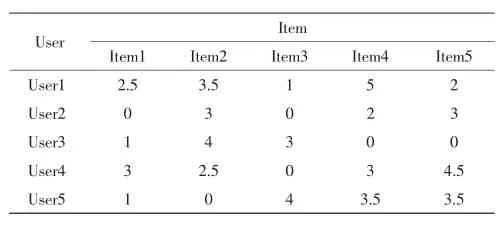
表1模拟数据Tab.1 Analog data

主要的实验数据示意图如表2所示.

表2小数据数据情况Tab.2 Small data sets

对自行构建的数据集进行聚合，可以看到选取的数据的关联度，没有完全的离散，关联度也不是特别高，符合新用户初期的使用情况：Number of clusters in input data=7，聚合后数据中心集合还不算太分散.同时给出统计后的小数据集数目，如图1和图2.

图1小数据集的分布示意图Fig 1 Distribution of small data sets

图2小数据集的聚合情况示意图Fig.2 Aggregation of small datasets

3.1 基本协同过滤处理

首先对数据进行预处理，在计算过程中，把数据分成训练集和测试集（不适用于虚拟数据集上，因为一方面只是为了构建流程，另一方面是数据很少，没有这个必要，所以用在MovieLens小数据集及之后的验证数据集），利用train_test_split中参数test_size设置为0.3，表示把70%划分为训练数据，30%划分为测试数据（train，test=train_test_split（data，test_size=0.3）），利用测试集进行最后的评估，衡量其结果的好坏.

其次分别进行上面提到的相似度指标计算，构建出传统的协同过滤模型，最后得到的相似用户.

对排在前面用户中的电影来进行推荐，记录此时的结果，并计算传统协同过滤模型下的RMSE.

3.2 基于SVD改进上面模型

经过SVD处理后，重新作为user-item-matrix data输入协同模型处理.

1数据预处理

item编号重新映射到从1开始的序列，与上面的协同过滤模型处理方式相同.

2随机划分数据集

依然利用train_test_split中参数test_size设置为0.3，70%划分为训练数据，30%划分为测试数据.

3构建user_item_matrix

该矩阵每一行代表一个user，每一列代表一个item，矩阵中的数字代表评分.

4对user_item_matrix矩阵进行SVD分解

得到SVD_prediction矩阵，作为新的user_item_matrix矩阵.

5然后继续进行协同过滤模型的步骤，最后计算模型的RMSE，进行评估.

4 实验结果与分析

4.1 实验结果

对虚拟数据集，根据流程里的公式，来计算相关性，以编号为1的用户为例：

按照相似性排序，并构造user-item-matrix，同时打乱顺序，进行处理，如表3.

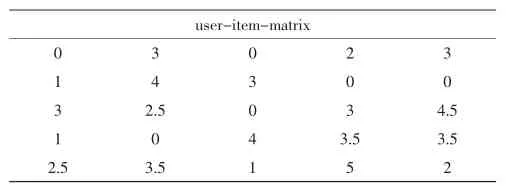
表3对虚拟数据集构建user-item-matrixTab.3 Building user item matrix for virtual datasetsuser-item-matrix

对原始数据来说，对比一下SVD-prediction（表4）和CF-prediction（表5）的预测，结果分别如下.

表4对虚拟数据集进行SVD-prediction处理结果Tab.4 SVD-prediction result of virtual data set

表5对虚拟数据集进行CF-prediction处理结果Tab.5 CF-prediction result of virtual data set

接下来对MovieLens小数据集进行验证并评估结果的好坏.针对此数据集，同样以编号为1的用户为例，计算出来的相似用户6，5，4，8，2，推荐的电影列表如表6.

表6相似用户列表Tab.6 List of similar users

对排在前面用户中的电影来进行推荐，在这里选取前五个进行列举，推荐电影列表如表7.

表7推荐电影名单Tab.7 List of recommended movies

4.2 评估结果

对推荐系统的研究一个重要的环节是如何评价一个推荐算法的好坏[6].本文以RMSE（Root Mean Squared Error）为评估指标将张量分解算法与传统协同过滤算法进行实验比较.在有限测量次数中，均方根误差常用式（1）表示，

RMSE评估指标见图3.

图3 RMSE指标评估结果Fig.3 RMSE index evaluation results

对比传统纯协同过滤或单独的SVD分解，RMSE值有了明显的降低

4.3 进一步验证结果

为了进一步验证其误差有明显降低，把数据量扩大，因为当数据集规模很大时，SVD分解会降低程序的速度，对后台离线运行了结果.数据的示意图见图4.

图4数据的分布示意图Fig.4 Distribution of data

同时给出统计后的数据集数目，见表8.

同样得出推荐列表，因为重点是要验证误差是否有降低，所以针对数据集，同样以编号为1的用户为例列表直接简单列出，见表9.

表8数据集数据Tab.8 Data sets

表9相似用户列表Tab.9 List of similar users

电影推荐结果为，[（Meet the Parents（2000）（Clockwork Orange，A（1971）（Wild Tales（2014）），（Horrible Bosses（2011）），（Cast Away（2000）），（Beethoven（1992）），（Along Came Polly（2004）），（50 First Dates（2004）），（Shining，The（1980）），（Stand byMe（1986）]

评估结果，见图5.

图5 RMSE评估指标结果Fig.5 RMSE evaluation index results

两次验证的结果表明，从实验数据来说，随着数据的增多，集中填充数据的增多，推荐的误差有一定减少，而且随着数据增多，误差减小量也增大，说明在传统协同过滤模型的基础上，对useritem-matrix进行SVD分解处理，再作为训练数据，输入协同过滤模型，会显著降低误差.

5 结论

本文通过验证的结果得出，在协同过滤算法的基础上，引入奇异值分解优化特征，利用SVD分解后svdprediction矩阵作为user-item-matrix应用于协同过滤模型进一步利用训练模型，这个改动会显著降低误差.协同过滤推荐算法作为是推荐系统中使用较广泛的算法之一，因此一点点改进都是有必要的.由于推荐系统存在冷启动问题，例如在初期新用户信息很少的情况下，或者在不完善的信息下，考虑到用户不一定会评分，也不一定愿意花时间留下太多信息，现实中用户很多时候并不能精确描述自己的需求信息，这就要用到需要推荐物品的属性，所以后期会对item本身所属的类别，属性赋以较大的权重，最后使模型更贴合实际生活[7].而且之后数据量也会增大，可以考虑是否利用聚类处理数据量的增大所以接下来打算引入时间序列、类别、标签等维度，利用张量分解[8-9]，来建立用户、物品、评分，时间，类别，标签等多维度的推荐系统[10-11].