基于k-medoids聚类算法的低压台区线损异常识别方法
2021-02-25薛明志陈商玥
薛明志,陈商玥,高 强
(天津理工大学电气电子工程学院,天津300384)
目前,国内外对低压台区线损的理论研究非常丰富.文献[1]采用了基于潮流计算的前推回代法,并对算法进行了改进同时引入三相不平衡、支路电压降对理论线损的影响,使得计算结果更为准确.随着理论算法研究的不断深入,逐渐将人工智能和神经网络引入到理论线损的计算中去,同样计算结果也更加贴合实际[2].文献[3]中通过建立主干线损耗、分支线损耗、接户线损耗、表计损耗这四个部分的数学模型进行技术线损的计算,此种算法需要的基础数据较多、计算量大.文献[4]描述了一种基于改进kmeans聚类和BP神经网络的台区线损率计算方法,以供电半径、低压线路总长度、负载率、居民用电比例为自变量,通过改进的k-means聚类算法将样本进行分类,再通过LM算法优化的BP神经网络算法计算台区线损率.文献[5]将径向基函数(radial basis function,RBF)神经网络应用到配电网线损的计算和分析中,并采用动态聚类算法确定RBF网格最优数,计算台区线损率.文献[6]建立了基于k-means聚类算法的数据预估模型,并将通过预测的线损率与实际线损率对比分析,找出线损率差异较大的台区.文献[7]提出了一种基于断面聚类的阶段理论线损计算方法,通过对断面网损的构成分析和断面数据分析,得出某时刻理论线损值和阶段理论线损值.文献[8-9]采用聚类分析算法,以采集系统采集得到的供电量、容量、负载率、用户数等作为输入量,进行聚类分析,通过对比对k-means聚类、两步聚类以及kohonen聚类这三种聚类算法,最终确定k-means聚类算法作为计算台区理论线损的算法模型.
可以看出,聚类算法和神经网络算法常应用于低压台区理论线损计算.但在国家电网公司中,有用电信息采集系统、同期线损系统等应用软件用于低压台区线损管理工作,能够实现单台区线损率的计算和表计参数的采集等功能,单纯整体线路理论线损的研究对实际工作来讲意义并不大.因此本文建立了基于k-medoids聚类算法的低压台区线损异常识别模型,通过日线损率数据实现台区线损稳定性的判断.
1 聚类算法和LOF算法模型
1.1 k-means聚类算法与k-medoids聚类算法
k-means聚类算法的原理比较简单,对于给定的数据样本,基于数据之间的欧式距离对数据划分成K个簇,通常旨在找到目标的最小平方差.具体表达式定义如下.
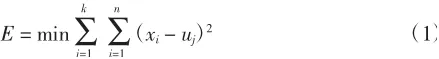
其中:E为数据簇最小平方差;xi为各个数据样本;uj为聚类中心点.
聚类中心点为每个簇内所有数据的均值,表达式如下.
k-means聚类算法原理简单、容易实现且收敛速度快,聚类效果也较好,算法易解释;但k-means聚类算法也有明显的缺点,当数据存在异常值时,会导致聚类效果差,存在凸数据时难以收敛,且对噪音比较敏感.
k-medoids聚类算法与k-means聚类算法主要区别在于聚类中心点的选择,k-means聚类算法聚类中心点为一组数据的均值,而k-medoids聚类算法的聚类中心点为一组数据中的某个值,选取的原则为与其他数据距离平方和最小的点.具体表达式如下.
其中:xi、xj为各个数据样本;M为数据方差的最小值.
聚类中心点uj为方差为M时的xj.
由于k-medoids聚类算法的中心点取自数据本身,因此能极大减小孤立点、凸数据等对数据运算结果的影响,因此本文采用k-medoids聚类算法.对于低压台区来讲,都是针对单个台区进行分析,因此聚类簇的个数为1.
在应用k-medoids聚类算法进行数据处理时,虽然能减小异常数据对聚类中心点的影响,但异常数据对于欧氏距离的计算结果依旧会产生极大的干扰,因此需要对数据源进行筛选和剔除.
1.2 局部异常因子LOF算法
采集系统在采集日线损率数据时,由于集中器故障、表计某一天采集不上数但第二天补招上数、故障表更换、采集掉线等短时能够恢复的故障会导致日线损率出现孤立点,这些孤立点虽然会导致部分台区出现短暂的异常,但解决问题后不能再当做异常台区处理.虽然k-medoids聚类算法能够避免聚类中心点受孤立点影响,但聚类的欧氏距离还是会受到孤立点的影响,而对低压台区线损是否异常的判断同时包含聚类中心点和欧氏距离两个影响因素.因此在数据聚类之前需对异常数据进行筛选和剔除.
由于日线损率数据分布不均匀,密度不同,异常值与正常数据偏差较大,像常用的四分位数、高斯分布在数据处理时很难达到预想效果,很容易因极大凸数据导致无法做出正确的筛选,因此本文采用局部异常因子(local outlier factor)LOF算法.LOF算法通过局部可达密度进行定义,如果一个数据与其他数据点比较疏远,那么这个点的局部可达密度就比较小.LOF算法衡量一个数据点的异常程度,并不是看它的绝对局部密度,而是看它跟周围邻近的数据点的相对密度.以数据点p为例,点p的局部相对密度(局部异常因子)为点p的k近邻平均局部可达密度与数据点p的局部可达密度的比值

首先根据局部异常因子的定义,如果数据点p的LOF值在1附近,则表明数据点p的局部密度跟它的邻居相近;如果数据点的LOF值小于1,则表明数据点p处在一个相对密集的区域,不大有可能是一个异常点;如果数据点p的LOF值远大于1,则表明数据点p跟其它点比较疏远,极有可能是一个异常点.
通过LOF算法可对日线损率数据的孤立点进行预先的筛选和剔除,再通过聚类算法对台区异常情况进行判断,这样的判断结果更为准确、可靠.
2 流程设计及数据处理分析
2.1 流程设计
本算法在传统聚类算法的基础上进行了改进,以k-medoids聚类算法为核心,以LOF算法作为日线损率数据优化的算法模型.线损率主要分为正常、高损和负损三种,线损率数值在0%~10%之间为正常,大于10%为高损,小于0%为负损.日线损率的统计数据需来源于智能表覆盖率为100%的台区,采集系统无法采集非智能表电量和数据,对存在非智能表的低压台区进行线损异常情况判定无意义.按照算法思路确定了低压台区线损异常识别的流程图,如图1所示.

图1基于聚类算法的低压台区线损异常识别流程图Fig.1 Flow chart of line loss anomaly recognition based on clustering algorithm
导入台区日线损率数据,通过局部异常因子LOF算法对异常数据进行筛选和剔除.
将去除异常值后的台区日线损率数据通过kmedoids聚类算法进行聚类分析,每个台区得到两个变量,一个是聚类中心点,用于初步判断台区是否异常;另一个是欧氏距离,欧式距离在计算时以聚类中心点为基础,主要反应台区日线损率的波动情况.由于实际测算时欧氏距离差别过大不利于台区线损稳定性的判断,因此在计算时将欧氏距离的结果除以台区日线损率数据的总个数,欧氏距离大于阈值则说明台区日线损率波动较大,可以判定台区线损存在异常需要进行治理,欧式距离在阈值以内则说明台区日线损率相对稳定,在聚类中心点合格的基础上可以判定台区线损正常.
2.2 局部异常因子LOF算法有效性分析
为验证上述算法的有效性,以某地区某低压台区(用N01台区命名)为例首先对LOF算法的数据处理性能、计算的准确度进行验证.该台区为期31天的日线损率数据见表1.
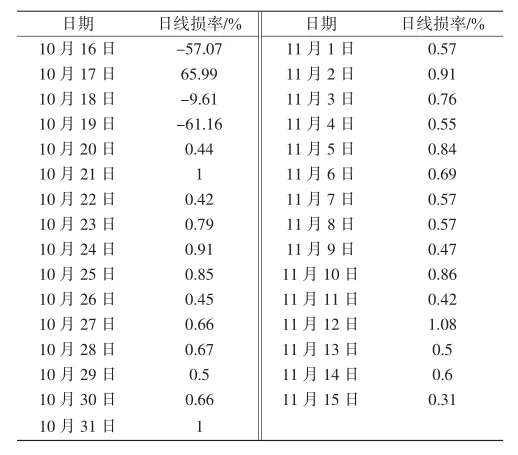
表1 N01台区为期31天日线损率数据Tab.1 31-day daily line loss rate data for N01
首先将日期转化成1-31的顺序序列,方便数据处理及图片绘制.N01台区日期与线损率的对应关系图如图2所示.
从表1及图2可以看出,N01台区前四天的日线损率数据波动较大,属于异常数据,通常可能是由于某块大电量用户某天采集不通,第二天采集调通后一天采集上了两天的电量,所以会导致前一天大高损,后一天又出现严重负损的情况.但四天后明显可以看出日线损率趋于稳定,且都属于正常的范围.对于此类存在异常数据的台区在聚类分析前明显需要剔除异常点,否则会导致在台区线损异常判断模型计算时出现误差,影响判断结果的准确性.
在选择局部异常因子LOF算法对异常数据进行筛选和剔除时,存在三个关键点:检测的邻域点个数k、异常点比例以及样本点的LOF值.

图2 N01台区日期与线损率对应关系图Fig.2 Corresponding relationship between the date of N01 and the line loss rate
算法中k值设置为20,k值过小会导致计算误差大,尤其是数据分布相对分散时;k值过大会导致计算复杂,增加计算量,因此在多次仿真试验后将k值定为20.
算法中异常点比例设置为0.1,相当于一组台区日线损率数据挑选三个异常值,异常点比例大会导致剔除过多的数据,容易将真实数据误认为异常数据剔除,影响实际线损稳定性的判断,经过反复仿真实验以及数据对比后最终将异常点比例设置为0.1.同时,若台区日线损率数据不存在异常值,剔除比例为0.1时对数据的分析也不会产生不良影响.
样本点的LOF值体现样本的局部密度,LOF值越大则表明样本点与其他数据越疏远,越可能是异常点,因此本文将LOF值最大的三个样本点作为异常点进行剔除.
N01台区日期与LOF值对应关系图如图3所示.
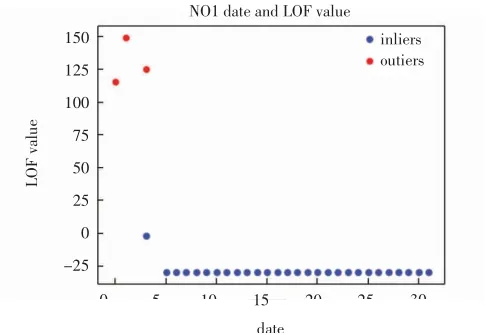
图3 N01台区日期与LOF值对应关系图Fig.3 The relationship between the date and the LOF value of station N01
图3中outliers表示异常点的LOF值,inliers表示正常点的LOF值.将LOF值偏大的第1、2、4个数据点进行剔除,而这三天的日线损率也是存在异常,远远偏离0%~10%的合格范围.
如图4所示,对异常点的数据进行了标识,与上述论证相对应.除了N01台区外,本文还选择了多个台区进行了数据仿真并对仿真结果进行了验证,经多次试验,仿真结果与N01台区类似,本文不再一一列举.

图4带异常点标识的N01台区日期与线损率对应关系图Fig.4 Correspondence diagram of date and line loss rate of N01 station area with abnormal point identification
这证明局部异常因子LOF算法能够有效的识别台区异常日线损率数据,能够实现异常数据判断、筛选和剔除功能.
2.3 聚类算法实例分析
引入LOF算法剔除异常值后,再通过k-medoids聚类算法实现台区是否存在异常的分析及判断.在应用matlab编译k-medoids聚类算法时,主要引入了两个变量,聚类中心点和欧氏距离.
聚类中心点表示离其他样本点距离平方和最小的样本点,主要反应某低压台区日线损率数据的中间水平.
欧氏距离表示以聚类中心点为基准,与其他样本点距离平方和再除以样本点的总个数,主要反应台区日线损率数据的波动水平.
本文主要以这两个参数实现台区线损是否存在异常的分析判断,如图1所示,通过多次计算机仿真测试后,最终将欧氏距离的阈值定为10(即欧氏距离小于等于10则认为其在合理的范围内).
通常来讲,对于低压台区线损是否存在异常的判断主要依靠一段时间内日线损率平均值法或直接观察法,直接观察法需逐个台区进行观测分析,虽然精准度高,但分析效率极低,不适合多个台区的分析治理.接下来选取天津市某地区819个台区作为数据样本,对平均值法、直接应用基于k-medoids聚类算法以及LOF算法优化后的k-medoids聚类算法这三种计算方法进行综合对比分析.
首先从819个台区中选取6个具有代表性的台区进行分析,台区日线损率数据以及分析数据见表2、表3.
如表2、表3所示,可以得出如下结果:
对于像N02台区这样线损稳定合格的台区,三种算法都能做出准确的判断;对于像N05台区和N06台区这样线损存在明显异常的台区也能做出准确的判断;
对于像N01台区、N03台区这样存在个别异常值的台区,LOF算法优化的k-medoids聚类算法能够做出准确的判断,但k-medoids聚类算法在判断时会出现异常,而平均值法能否做出准确的判断则需要依靠日线损率数据异常值偏离正常值的程度,对N01台区平均值法的判断便出现了错误,而对N03台区却做出了正确的判断,这说明平均值法对此类情况的判断稳定性低,容易出现偏差;
对于像N04台区这样平均线损率和聚类中心点均合格但台区线损却明显存在异常的台区,平均值法做出了错误的判断,而后两种算法都能根据欧氏距离做出正确的判断.
可以看出,三种算法对于线损率稳定合格或稳定不合格的台区均能做出准确的判断;但对于线损率存在异常波动的台区,只有LOF算法优化的kmedoids聚类算法能够实现准确的判断,平均值法存在随机性,而k-medoids聚类算法的判断容易受到异常数据的影响.
在选取6个典型台区进行分析的同时,对819个台区的总体情况也进行了归纳,如表4和图5所示.
从表4和图5可以看出,平均值法测算的正常台区和负损台区最多,高损台区三种算法相差不大,由于线损异常是根据欧氏距离判断的,所以平均值法的线损异常台区为0;k-medoids聚类算法测算的正常台区数远远小于其他两种算法,负损台区数在其他两种算法之间,而线损异常台区数相对较高;LOF算法优化的k-medoids聚类算法测算的正常台区数与平均值法相差不大,但负损台区数最少,而异常台区数不到k-medoids聚类算法测算数量的一半.
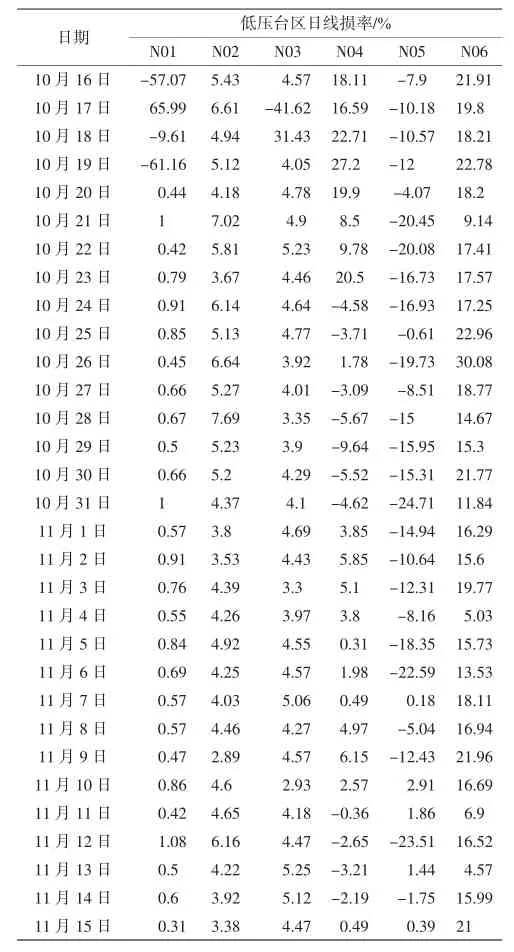
表2 N01等6个台区为期31天日线损率数据Tab.2 31-day daily line loss data for 6 stations including N01
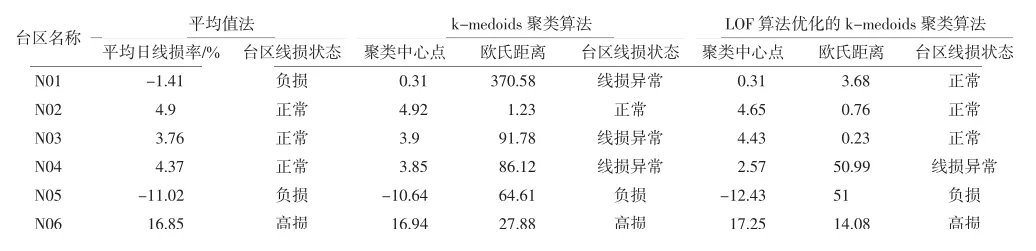
表3 N01等6个台区不同算法处理结果对比分析表Tab.3 Comparison and analysis table of different algorithm processing results of 6 stations including N01

表4台区线损情况对比分析表Tab.4 Comparative analysis table of line loss

图5台区线损情况对比分析图Fig.5 Comparative analysis of line loss
通过以上的数据分析及实例验证,可得出如下结果:
平均值法在判断台区线损是否存在异常时存在数据上的巧合性,有较大的误差,无法识别台区日线损率波动较大的台区,导致虽然判断结果为合格台区,实际却是异常台区的现象出现;
k-medoids聚类算法在判断台区线损是否存在异常时会因为异常日线损率数据导致判断结果出现错误,将一些合格台区认定为异常台区;
LOF算法优化的k-medoids聚类算法能够有效的避免因日线损率波动和异常值引起的判断错误,能够有效的识别线损异常低压台区.
在算法的实际应用上,台区日线损率数据选择的日期及天数可根据需求进行改变,算法根据给定的任意连续台区日线损率数据即可实现对台区线损是否存在异常的判断,应用的灵活性很高,但为了保证计算的准确度,日线损率数据一般不应小于10个.
3 结论
本文依托用电信息采集系统日线损率数据,结合LOF算法和k-medoids聚类算法确定了LOF算法优化的k-medoids聚类算法模型,应用此算法模型实现了低压台区线损异常情况的判断,并通过819个低压台区的日线损率数据验证了该算法模型对于低压台区线损异常判断的有效性、合理性和实用性.
