对一道有关动点的轨迹题解法的探究

陈琳

立体几何问题的命题方式比较多，如判断点、线、面之间的位置关系、求空间角的大小、求空间距离的大小、与动点有关的轨迹问题等，其中与动点有关的轨迹问题的综合性较强，对同学们的空间想象能力和抽象思维能力的要求较高.本文以一道题为例，谈一谈解答与动点有关的轨迹问题的两种思路.

例题：如图1，在四棱锥P-ABCD中，四边形ABCD是边长为2的菱形，∠DAB=60°，PA=PD，∠APD=90°，平面PAD⊥平面ABCD，点Q是△PBC内（含边界）的一个动点，且DQ⊥AC，则点Q所形成的运动轨迹的长度为_____.

本题不仅考查了四棱锥的特征和性质、面面垂直的性质定理，还考查了与动点有关的轨迹问题，难度较大.解答本题，需首先根据题意明确各点、线、面之间的位置关系，确定动点Q的运动轨迹，建立与动点Q相关的关系式.本题有以下两种解题思路.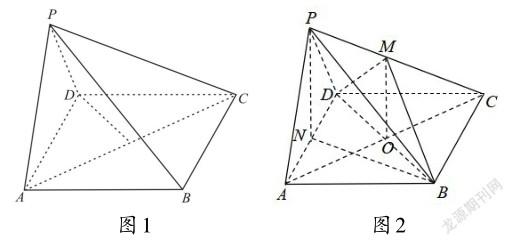

一、利用平面几何知识求解

运用平面几何知识解答立体几何中与动点有关的轨迹问题，关键在于将点、线、面之间空间位置关系转化到某个平面中，将空间几何问题转化为平面几何问题，借助平面几何知识，如勾股定理、点到直线的距离公式、正余弦定理、等边三角形的性质等来解题.对于本题，我们可以根据题意添加合适的辅助线，将四棱锥中的点、线、面的位置关系转化到△PAC、△MOC、△BCM中，再运用勾股定理、余弦定理、直角等腰三角形的性质、等边三角形的性质求得点Q所形成的运动轨迹的长度.

解：连接BD交AC于点O ，在PC上取一点M，连接MB、MD，使得MD⊥AC，如图2所示，

∵DM⊥AC ， AC⊥BD ， DM？BD=D ，

∴AC⊥平面DBM ，

∴只要使点Q在平面DBM与侧面PBC的交线上即可，即点Q的轨迹是线段BM，连接MO ，

∵直线AC⊥平面DBM ，

∴AC⊥MO ，∴△MOC为直角三角形，

取AD中点N ，连接PN，BN ，

∵△PAD是直角等腰三角形，△BAD是等边三角形，

∴AD⊥PN ， AD⊥BN，

又PN？BN=N ，平面PAD⊥平面ABCD ，平面PAD？平面ABCD=AD ，

∴AD⊥平面PNB ， PN⊥平面ABCD，

二、借助空间向量法求解

空间向量法是解答立体几何问题的常用方法.运用空间向量法解题，要根据已知点、线、面的位置关系构建合适的空间直角坐标系，通过空间向量的运算来求得问题的答案.对于本题，我们根据题意可以确定AC⊥平面BDM，于是以O为坐标原点，OA为x轴、OB为y轴建立如图3所示的空间直角坐标系，给各个点、线段赋予坐标、向量，运用空间向量的加法、减法、数乘运算法则、空间向量基本定理以及模的公式求得问题的答案.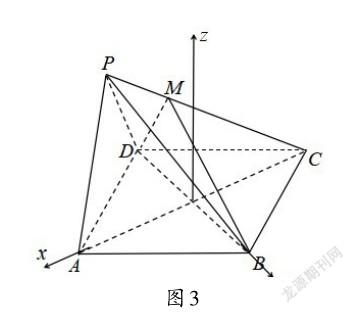

解：如图3，连接BD交AC于点O，

∵四边形ABCD为菱形，∴AC⊥BD，

在PC上取一点M，连接MD，MB ，

∴DM⊥AC ，又AC⊥BD，BD？DM=D ，

∴AC⊥平面BDM ，則点Q的轨迹为BM，以O为坐标原点，OA为x轴，OB为y轴建立如图3所示的空间直角坐标系.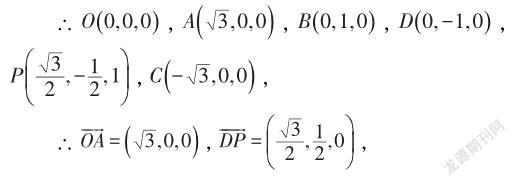

虽然立体几何中与动点有关的轨迹问题较为复杂，但是我们只要将空间几何问题转化为平面几何问题，利用平面几何知识求解，或建立空间直角坐标系，通过空间向量运算来求解，也能使问题顺利得解.相比较而言，利用平面几何知识求解的过程较为复杂，借助空间向量法解题的思路较为简单但运算量较大.同学们在解题时可根据解题需求选择最优的解题方案.

（作者单位：江苏省泰兴市第一高级中学）