基于联合集合卡尔曼滤波的锂电池SOC 估计

陈 刚，储建新，潘炫霖，雷健新，郑 迪

（1.国网浙江海盐县供电有限公司，浙江 嘉兴 314300；2.中国计量大学，杭州 310018）

0 引言

锂离子电池具有能量比高、循环寿命长和自放电率低等特点，除应用于电动汽车、电子产品等领域外，还被逐渐应用于移动储能领域。相比于传统柴油发电机，基于锂电池的移动储能装置具有清洁、噪音小、便于控制和监测等优势，有着广阔的应用前景[1]。

锂电池SOC（荷电状态）是指一定放电倍率下当前剩余容量与额定容量的比值，是锂电池的重要参数。SOC 的准确估计是实现锂电池能量管理、均衡控制等功能的基础。目前，在锂电池SOC估计方面已积累了大量研究成果，根据原理的不同主要可以分为安时积分法[2]、开路电压法[3]、基于人工神经网络的方法[4]、卡尔曼滤波及其改进方法等。其中安时积分法通过对放电电流的积分来估计当前SOC，难以克服累计误差；开路电压法需要使锂电池长时间静止来获得准确的开路电压数据，不适合在线使用；人工神经网络是一种具有自主学习能力的多层反馈系统，将其非线性适应性信息处理能力应用于锂电池的状态估计中，主要包括BP 神经网络[5]等单神经网络估算方法、基于深度学习的估算方法[6]以及与其他算法结合的复合神经网络方法[7]等，这些方法需要大量实验数据来训练网络参数，在有限的样本数量下估计精度可能受到限制；KF（卡尔曼滤波）采用最小二乘法，结合锂电池的数学模型可实现对SOC 的最优估计。为克服KF 只能处理线性系统的缺点，文献[8]通过观测状态的一阶泰勒展开将非线性系统转换为线性系统，从而提出了EKF（扩展卡尔曼滤波）。在此基础上，在模型改进方面，文献[9]采用微分阶等效电路模型来实施EKF。文献[10-11]在EKF 计算中分别计及了锂电池迟滞效应和热耦合。在算法改进方面，文献[12-13]分别提出了自适应EKF、有限差分EKF 等方法，从估计初始值、噪声协方差修正等方面来改善EKF的估计精度。此外，为计及模型参数时变特性的影响，文献[14]设计了双EKF 算法来同时估计锂电池SOC 和模型参数。然而，EKF 的一阶泰勒展开忽略了高阶项，可能会在高度非线性系统的状态估计中引入较大的截断误差。同时，EKF 需要计算雅克比矩阵，对计算能力要求较高。为此，文献[15-16]利用无迹变换处理状态变量，通过构造Sigma 点的期望和协方差矩阵来传递状态变量特征，从而提出了基于UKF（无迹卡尔曼滤波）的SOC 估计方法，具有较高的估计精度和更好的鲁棒性。针对噪声先验统计特征未知的问题，文献[17]提出基于自适应UKF 的SOC 估计方法，在估计SOC 过程中自动调整噪声协方差。为提升算法鲁棒性，文献[18]提出模糊UKF 来估计SOC，然而UKF 计算高维协方差矩阵同样带来了较大的计算负担。EnKF（集合卡尔曼滤波）是由Evensen提出的一种数据同化方法[19]，被广泛应用于天气预报、图像重构等领域。EnKF 将蒙特卡罗方法应用于KF 框架，用样本集合的统计特征来近似表征状态变量，避免了EKF 中的线性处理，也无需计算复杂的协方差矩阵，因此具有较好的准确性和较高的计算效率[20]。

本文建立了锂电池的改进等效电路模型，在Thevenin 模型的基础上考虑了迟滞效应的作用。采用实验方法对该模型的参数进行辨识，并得到开路电压的表达式。在此基础上，分析了EnKF的原理并提出了基于联合EnKF 的SOC 估计方法，从而避免了充放电过程参数演变引起的SOC估计误差。分别在DTS（动态应力测试）和FUDS（联邦城市驾驶序列）工况下与EKF 和UKF 进行对比，证明了该方法具有更好的准确性和更高的计算效率。

1 锂电池等效模型

1.1 等效电路模型

根据锂电池的工作原理，通常可采用电化学模型、等效电路模型和神经网络模型等来描述其工作状态和动态特性[21]。其中，等效电路模型具有应用方便、易于理解等优点，被广泛用于锂电池建模和状态估计中。根据结构不同，锂电池等效电路模型可分为Rint 模型、Thevenin 模型、PNGV 模型和GNL 模型等[22]。本文采用Thevenin模型作为锂电池的等效电路模型，该模型具有结构相对简单、参数易识别、能较好地表征电池动态特征等优点。

Thevenin 模型原理如图1 所示，其中Uocv为开路电压，是与当前SOC 和环境温度相关的变量；Ut为端口电压；I 为电流，电池放电时I>0，反之I<0；R0为内阻；R1和C1分别为表征电池极化效应的电阻和电容；U1为极化电容两端电压，以图1 中所示电流方向为正方向。

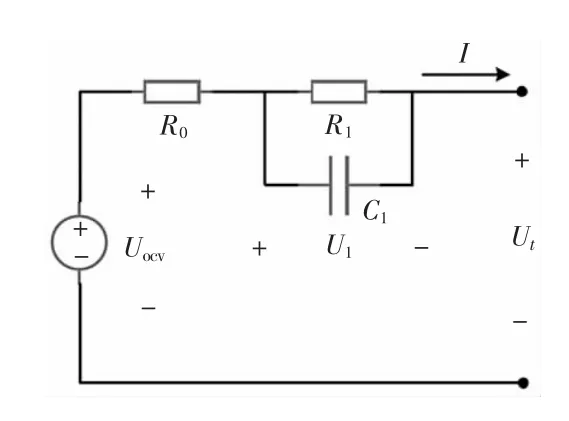
图1 Thevenin 原理图

根据锂电池Thevenin 模型原理图，可得其电路方程为：

根据锂电池SOC 的定义，其可表示为：

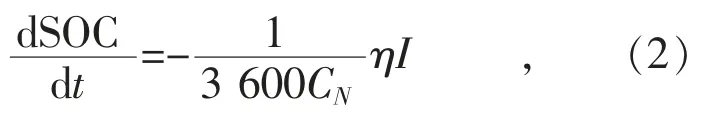
式中：CN为锂电池额定容量；η 为库伦效率。

式（1）和式（2）中的微分项为连续变量，将其离散化为：

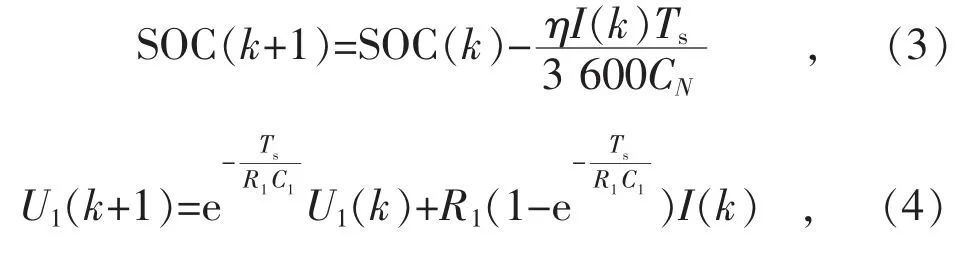
式中：k 为时刻；Ts为采样周期。

1.2 等效电路模型参数辨识

为实现锂电池SOC 的在线估计，需掌握锂电池等效电路模型的参数，需要辨识的参数内阻包括R0，R1和C1。本文选择的实验对象为单体磷酸铁锂电池，其额定容量为1 130 mAh，额定电压为3.5 V。

为辨识等效电路模型的参数，采取以下实验步骤：首先将SOC 为100%的锂电池静置一段时间以达到稳定状态，其次以1 C 电流放电12 min，再静置一段时间。实验过程中锂电池电流和端电压波形如图2 所示。

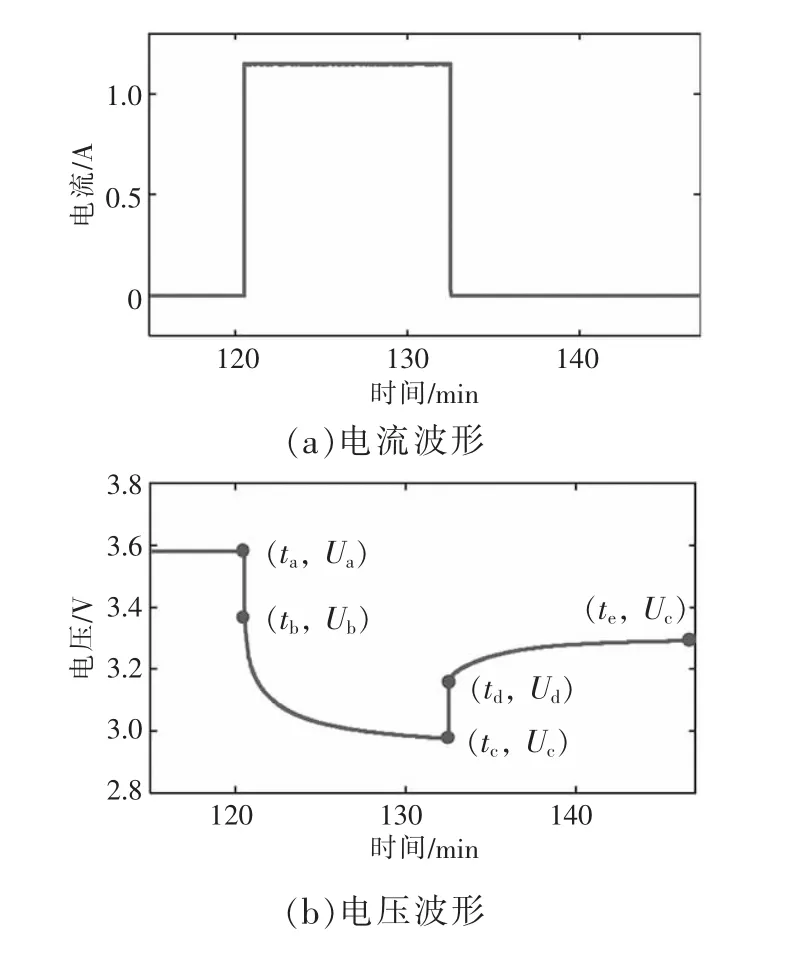
图2 锂电池实验过程电流、电压波形

该实验通过电压的动态变化来反应等效电路参数的响应。图2（b）中，Ua～Ub段和Uc～Ud段的瞬间变化反映的是电流突变时内阻R0上的电压变化，而Ud～Ue段则可视为等效电路的零输入响应，反映了极化电容对电压变化的阻碍作用。由此可列出3 个待辨识参数的表达式：

1.3 开路电压与SOC 的关系

采用以下方法对锂电池进行实验，来获得其开路电压与SOC 的关系。将锂电池充满至100%的SOC，静置一段时间后采用C/25 的小电流放电；放电至最小截止电压2.0 V 后静置一段时间并采用相同倍率小电流开始充电，直到达到最大截止电压3.6 V。对离散的采样点插值，得到如图3 所示的充、放电的实验曲线，进一步对充、放电曲线取平均值，得到开路电压Uocv-SOC 的平均曲线。

图3 开路电压与SOC 的关系曲线

2 集合卡尔曼滤波

与其他卡尔曼滤波方法类似，EnKF 是一种基于采样的非线性滤波方法，其将蒙特卡罗方法运用于KF 方法中，不必计算高维的协方差矩阵和雅克比矩阵，从而可有效提升计算效率，具有更好的鲁棒性，在状态估计问题上具有良好的应用前景。

对于一个非线性系统，其第k 时刻状态方程和测量方程可分别表示为：

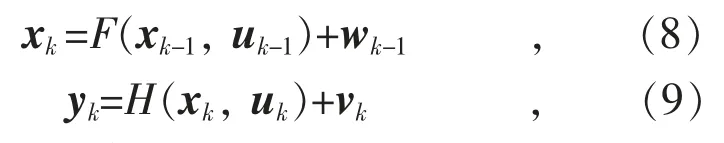
式中：x，u，y 分别为系统状态变量、输入变量和输出变量；F 和H 分别为系统状态方程和测量方程；w 和v 分别为系统过程噪声和测量噪声，w～N（0，Q），v～N（0，R），Q 和R 分别w 和v 的协方差矩阵。

将EnKF 用于该系统的状态估计时，先从状态变量xk的先验分布中抽取N 个样本，构成状态变量集合再在每个时刻重复以下2 步：

（1）预测。根据上一时刻后验状态变量集合和过程噪声集合预测当前时刻先验状态估计，即有：

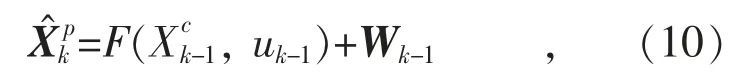
式中：上标^ 表示估计值；p 表示k 时刻的先验状态估计；c 表示k-1 时刻后验状态估计；Wk-1=为过程噪声集合。

（2）更新。根据当前时刻先验状态估计计算系统测量估计：

根据测量估计与实际测量的偏差来计算滤波器增益：

利用测量偏差和滤波器增益修正状态估计值，得到当前时刻的后验状态估计：

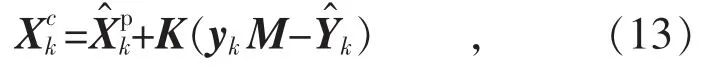
式中：M 为m×N 的全1 矩阵，m 为变量y 的维度。后验状态估计集合的平均值即是当前时刻对系统状态的最优估计。

3 基于联合EnKF 的锂电池SOC 估计

根据第1 节中建立的锂电池等效电路模型，以SOC 和极化电容两端电压U1作为状态变量，同时为表征充、放电过程中等效电路模型参数的变化，将R0，R1，C1作为补充的状态变量，用随机噪声来表征参数的动态演变，在递推过程中与状态变量进行联合估计，则系统状态变量和参数变量可分别表示为：

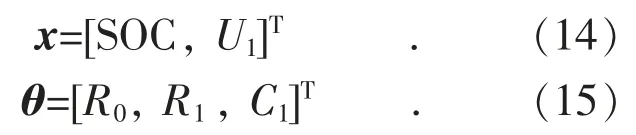
测量变量y 为锂电池端电压Ut，输入变量u为锂电池电流I，可提出基于联合EnKF 的锂电池SOC 估计方法，对锂电池SOC 和等效模型参数联合估计，其算法流程如图4 所示。具体步骤为：

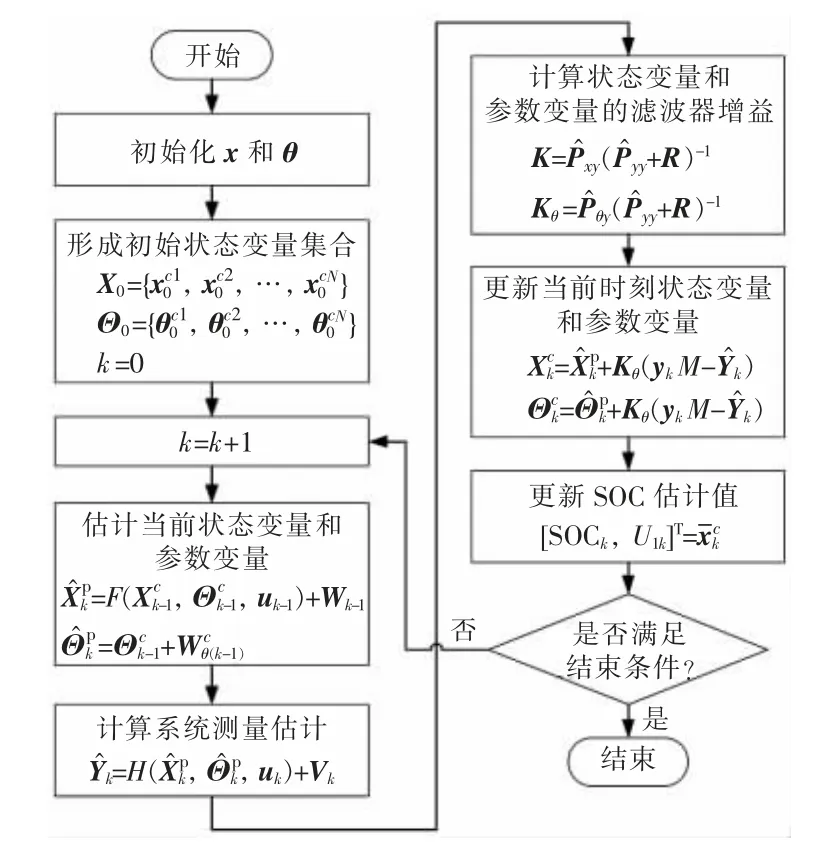
图4 基于联合EnKF 的锂电池SOC 估计方法流程

（1）初始化状态变量x 和参数变量θ，以充满状态[1，0]T作为状态变量x 的初始值，以辨识出的模型参数作为参数变量θ 的初始值。

（2）从状态变量x 和参数变量θ 的先验分布中分别抽取N 个样本，分别构成集合

（3）在第k 时刻估计当前时刻的状态变量和参数变量：

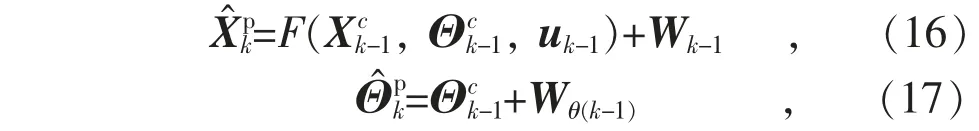
（4）在第k 时刻估计当前时刻的系统测量变量：

（5）分别计算状态变量和参数变量的滤波器增益：

（6）更新第k 时刻的状态变量和参数变量：

4 实验验证与分析

本节分别针对DTS 和FUDS 工况下的锂电池SOC 进行估计，并与EKF 和UKF 方法进行对比，从而验证所提出的联合EnKF 方法的有效性。用于实验验证与分析的数据来自马里兰大学CALCE的锂电池开源数据集，其采用Arbin BT2000 测试仪及其配套充放电控制软件对锂电池进行充放电实验[3]。数据分析和程序设计平台为MATLAB 2019b，程序运行环境为Intel i7 9700K@3.6 GHz。

4.1 DTS 工况实验

DTS 工况下设定温度为25 ℃，电池电流波形如图5 所示。设定联合EnKF 集合样本数为100，在该工况下联合EnKF 方法对SOC 的估计结果如图6 所示。由图6 可知，在放电过程中模型内阻R0、极化电阻R1及极化电容C1均随SOC 而变化，但SOC 估计值曲线与实验测量曲线基本吻合，均方根误差0.58%，平均绝对误差0.48%，最大绝对误差1.15%，具有较高地估计精度。

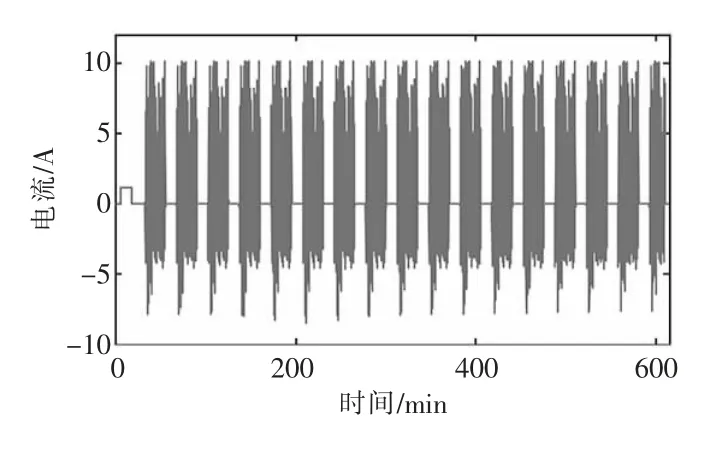
图5 DTS 工况下锂电池电流波形

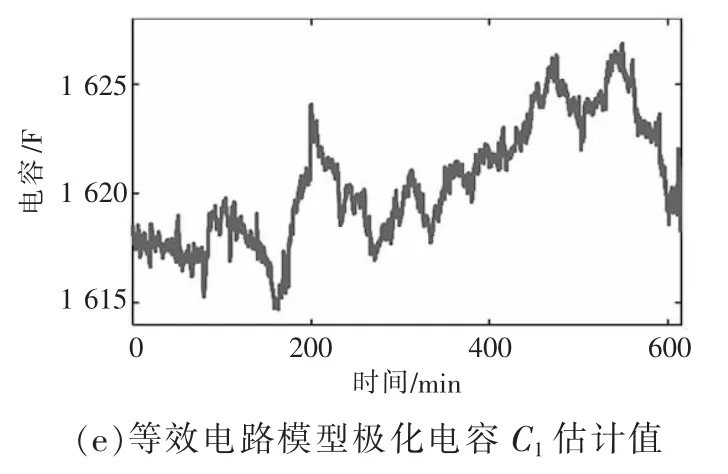
图6 DTS 工况下联合EnKF 的估计效果

分别采用UKF 和EKF 与联合EnKF 对DTS工况下锂电池SOC 的估计效果进行对比，对比结果如图7 和表1 所示，其中平均运行时间是指全部迭代过程中每次迭代计算的平均时长。由表1 可知，在各项误差指标上联合EnKF 的精度相比于其他2 种方法均有所提高，同时联合EnKF的运行时长小于EKF 和UKF，表明该方法计算效率更高。

表1 不同估计方法的效果比较

图7 DTS 工况下3 种方法估计效果对比

4.2 FUDS 工况实验

采用不同温度下FUDS 工况进一步检验所提联合EnKF 方法的有效性。如图8 所示为FUDS工况下的锂电池电流波形，该工况相对于DTS 工况电流变化更大且更随机。如图9 所示为不同温度下采用联合EnKF 对锂电池SOC 的估计结果。由图9 可知，不同温度下联合EnKF 对锂电池SOC 的估计误差均较为稳定，10 ℃，25 ℃，40 ℃下的均方根误差分别为0.45%，0.57%，0.54%，表明在不同温度下所提联合EnKF 均有较好的适应性。

图8 FUDS 工况下锂电池电流波形

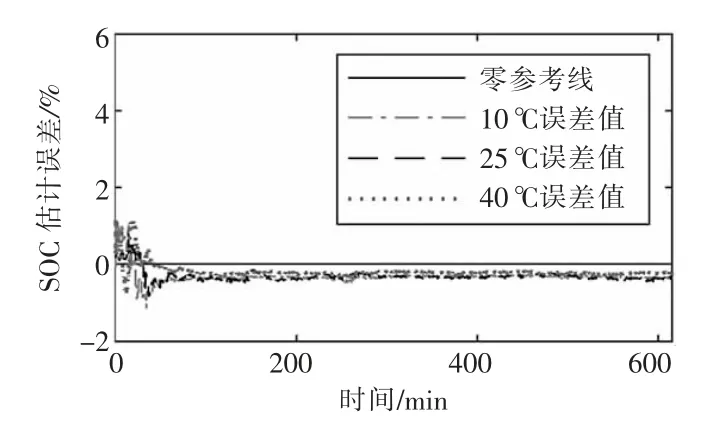
图9 不同温度FUDS 工况下联合EnKF 的估计效果

4.3 集合样本数量影响分析

集合样本数量是联合EnKF 算法的重要参数，当集合样本数量太小时，可能使其统计特性大幅偏离状态变量，从而导致滤波器不收敛。提高集合样本数量时可降低随机抽样引起的偏差，提高SOC 估计准确性，但也将降低计算效率。为分析集合样本数量与算法准确性和效率之间的关系，在DTS 工况下分别设定集合样本数量为100，200，300，500，1 000，1 500 和2 000，在每个集合样本数量下运行20 次程序，计算程序每次运行的平均运行时间和RMS（均方根误差），结果如图10 所示。

由图10 可知，在样本数较小（N<500）时，增大样本数可取得较好的精度提升效果，同时运行时间变化不大；在样本数较大（N>1000）时继续增大估计精度变化较小，而运行时间则显著增加。由此，需在权衡准确性和计算效率的条件下选择集合样本数量。

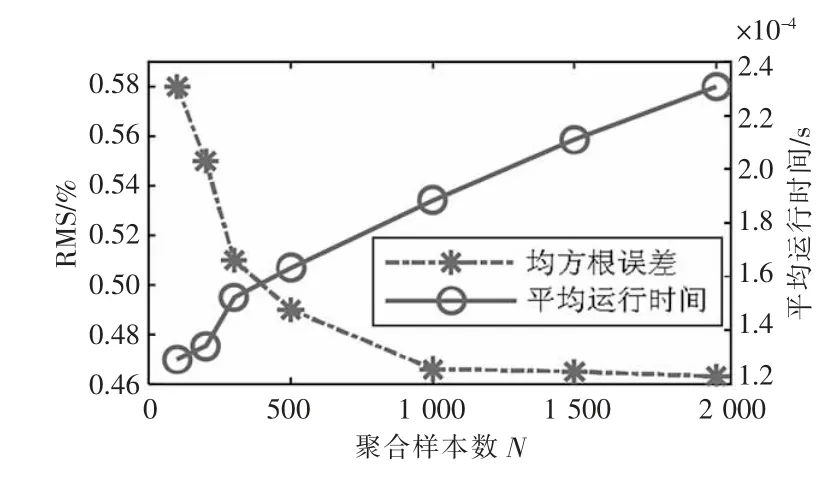
图10 不同集合样本数下联合EnKF 对SOC 估计的均方根误差和算法平均运行时间比较

5 结语

针对现有KF 方法估计SOC 时需要计算高维雅克比矩阵或协方差矩阵，导致计算效率和估计准确性不足的问题，提出了基于联合EnKF 的锂电池SOC 估计方法。该方法以锂电池等效电路模型为基础，充分考虑了锂电池充放电过程中模型参数的变化，以集合的统计特征来表征状态变量，避免了高维雅克比矩阵或协方差矩阵逆矩阵的求解，具有较高的计算效率和精度。实验结果表明，该方法在DTS 和FUDS 工况下均具有较高的估计精度，同时相比于EKF 和UKF 的SOC 估计方法，该方法可有效提高计算效率，具有较好的应用前景。