砂砾石地基上水闸底板弯矩预测的多元非线性回归模型
2021-02-24孙淑华王梓优
孙淑华,王 建,何 露,王梓优
(1.河海大学水利水电学院,江苏 南京 210098;2.南京水利科学研究院大坝安全与管理研究所,江苏 南京 210098)
水闸是实现水资源优化配置的重要建筑物[1-2]。底板作为闸室结构的基础,其结构安全决定了水闸工程整体的安全与稳定。砂砾石地基性质处于基岩与软基之间,地基承载力较好,压缩性较小。对砂砾石地基上的水闸而言,闸墩传递的竖向荷载与底板传递的竖向荷载相差较大,地基沉降差也较大,底板应力高,因此底板弯矩预测是设计的重要内容。
水闸设计中,设计人员通常利用底板弯矩计算底板应力和底板配筋量。目前用于水闸底板弯矩计算的工具主要有MDSolids系列和理正工具箱等,这些计算软件以材料力学和结构力学为理论基础,计算方法简单,但无法考虑闸段与闸段之间的接触效应,计算精确度不高。20世纪中期开始,计算机迅速普及,有限元法应运而生[3-9]。目前,随着有限元技术的逐渐完善和迅速普及,有限元技术在水闸工程中的应用也较为广泛。例如:苏燕等[10]针对新疆某渠首工程泄洪闸有底坎折线型闸底板的特殊形式,论证了用理想弹塑性有限元进行水闸结构分析的可行性;苏超等[11]以江苏省宜陵北闸改造工程为例,采用有限单元法分析了不同加载方法在水闸改造工程结构应力计算中的差异。
回归分析方法是一种探求变量之间关系的统计方法和技术,回归分析又分为线性和非线性回归分析[12]。目前,关于线性回归分析的研究方法和应用已相对成熟[13-15],然而,非线性回归分析的发展相对滞后且缓慢,需要庞大且复杂的计算过程。随着计算机技术的进步和计算软件的迅速发展,非线性回归分析的研究和应用也得到了快速发展[16-18]。在非线性回归分析中,多元非线性回归分析是通过对多个变量组成的非线性回归方程进行拟合而获得模型,其中,通过非线性最小二乘法估计模型的未知参数是最广泛的做法。目前,多元非线性回归模型运用广泛[19-23]。例如,胡荣光[24]建立了基础沉降量与填筑高度、弹性模量、压缩层厚度、时间之间的多元非线性回归模型,并采用现场实测数据验证了模型的普适性;刘斯凤等[25]研究了多因素(掺合料种类、水胶比、养护龄期、加速腐蚀制度)作用对钢筋混凝土握裹力的影响,建立了多因素共同作用影响钢筋混凝土握裹力变化的多元非线性回归分析模型。
为了给设计人员提供一种方便又准确地计算底板弯矩的方法,加快设计进度,本文利用有限元法计算多组考虑接触作用的底板弯矩值,研究了水闸底板厚度、闸孔宽度、闸墩高度、砂砾石地基厚度4个因素对底板弯矩的影响规律,结合工程实际,基于多元非线性回归分析,建立底板中心弯矩预测模型,并对模型的预测效果进行检验。
1 水闸参数对底板弯矩的影响规律
本文以福建省莒口闸为例,考虑闸孔宽度、底板厚度、闸墩高度、砂砾石地基厚度、弹性模量、闸墩荷载等因素的影响,建立包含基岩、砂砾石层、底板、闸墩的整体三维有限元模型,生成高质量三维实体单元。其中,垫层、防渗墙采用C15混凝土,闸底板、闸墩等结构采用C30混凝土。砂砾石地基的弹性模量为200 MPa,泊松比为0.2。有限元网格单元尺寸为0.5~1 m,整体有限元网格模型如图1所示。

图1 水闸整体有限元模型
采用接触算法考虑分缝两侧闸墩的相互作用以及防渗墙与砂砾石地基间的相互作用。模型计算结果表明,从各单项荷载的计算结果来看,自重是底板应力的控制性荷载,其效应占总荷载的80%左右。因此,本文中的底板应力分析及预测均基于自重荷载进行。
水闸底板弯矩分布如图2所示,可见底板中心弯矩绝对值最大,闸墩底部弯矩绝对值略小于底板中心弯矩绝对值;双孔或单孔闸段最大弯矩以及弯矩分布规律接近,因此,本文针对双孔闸段进行分析。

图2 某水闸底板弯矩分布
本文采用控制变量法研究各参数对底板中心弯矩的影响规律。
a. 底板厚度。底板厚度影响底板底面地基反力分布,从而影响底板中心弯矩。因此,底板厚度对底板中心弯矩的影响较为复杂。在实际工程中,因水闸荷载不大,水闸实际采用的底板厚度范围为1.5~2.5 m。取底板厚度分别为1.0 m、1.5 m、2.0 m、2.5 m,控制闸孔宽度为16 m、闸墩高度为20 m、砂砾石地基厚度为10 m,得到底板中心弯矩与底板厚度的关系如图3所示。由图3可见,随着底板厚度的增加,底板中心弯矩呈非线性增加,底板中心弯矩-底板厚度曲线有斜率变缓的趋势,变缓速度较小。

图3 底板中心弯矩与底板厚度关系
b. 闸孔宽度。闸孔宽度变化导致底板长度增加,同时影响底板荷载分布,两个因素共同作用,造成底板中心弯矩变化。水闸一般采用8 m以上的孔径,目前国内最大的孔径为30 m。取闸孔宽度分别为8 m、10 m、12 m、14 m、16 m,控制底板厚度为2 m、闸墩高度为20 m、砂砾石地基厚度为10 m,得到底板中心弯矩与闸孔宽度的关系如图4所示。由图4可见,随着闸孔宽度的增加,底板中心弯矩呈非线性增加,底板中心弯矩-闸孔宽度曲线有斜率变缓的趋势,变缓速度较大。

图4 底板中心弯矩与闸孔宽度关系
c. 砂砾石厚度。深层砂砾石地基对底板中心弯矩影响较小,浅层砂砾石地基对底板中心弯矩影响更为显著。平原上砂砾石地基的厚度一般小于30 m。取砂砾石厚度分别为3 m、5 m、10 m、15 m、20 m、30 m,控制底板厚度为2 m、闸孔宽度为16 m、闸墩高度为20 m,得到底板中心弯矩与砂砾石厚度的关系如图5所示。由图5可见,随着砂砾石厚度的增加,底板中心弯矩呈非线性增加,底板中心弯矩-砂砾石厚度曲线有斜率变缓的趋势,变缓速度较大,且大于底板中心弯矩-闸孔宽度曲线斜率的变缓速度。

图5 底板中心弯矩与砂砾石厚度关系
d. 闸墩高度。闸墩高度变化相当于闸墩上部荷载变化,与底板中心弯矩的关系较简单。闸墩高度参数的选取主要与水位高度有关,在已建成的水闸中,闸墩高度大多在10 m左右。取闸墩高度分别为5 m、10 m、15 m、20 m,控制底板厚度为2 m、闸孔宽度为16 m、砂砾石地基厚度为10 m,得到底板中心弯矩与闸墩高度的关系如图6所示。由图6可见,随着闸墩高度的增加,底板中心弯矩呈线性增加。
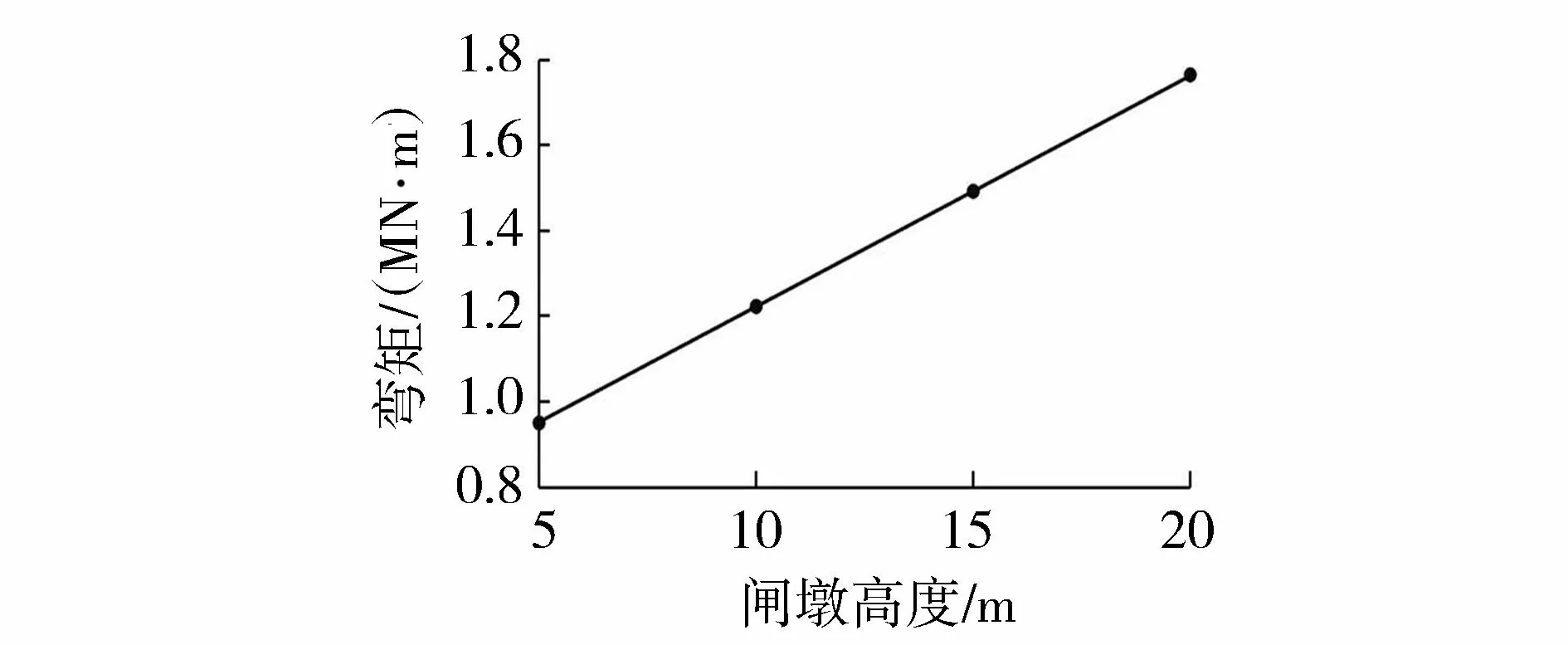
图6 底板中心弯矩与闸墩高度关系
2 多元非线性回归模型
由前文分析可知,水闸底板厚度、闸孔宽度、闸墩高度、砂砾石地基厚度这4个因素都对底板中心弯矩影响显著。底板中心弯矩与底板厚度、闸孔宽度、砂砾石地基厚度呈非线性关系,在预测模型中,可分别选取3个参数参与训练。底板中心弯矩与闸墩高度呈线性关系,在预测模型中,可选取2个参数参与训练。
本文利用matlab非线性回归内置nlinfit函数,采用最小二乘估计法,建立影响因素与底板中心弯矩间的非线性函数关系式。其中,水闸闸墩高度与底板中心弯矩呈线性函数关系,可表示为
y=mx3
(1)
式中:y为底板中心弯矩,MN·m;x3为闸墩高度,m;m为系数。
底板厚度、闸孔宽度、砂砾石地基厚度与底板中心弯矩呈非线性函数关系,可表示为
(2)
式中:xi为底板厚度、闸孔宽度或砂砾石地基厚度,m;l、n为系数。
因水闸底板厚度、闸孔宽度、闸墩高度、砂砾石地基厚度这4个因素共同作用于底板中心弯矩,为考虑4个自变量之间的相互影响,将函数形式设为
(3)
式中:x1为水闸底板厚度,m;x2为闸孔宽度,m;x4为砂砾石地基厚度,m;a为水闸底板厚度参数;b为闸孔宽度参数;c为闸墩高度参数;d为砂砾石地基厚度参数;k为总体回归参数。
3 水闸底板中心弯矩预测
将不同类别的设计参数排列组合,形成表1中的54组水平组合。将表中每一组水平组合作为水闸结构的几何参数,基于已建好的有限元模型,利用ABAQUS进行计算,得到底板中心的弯矩值。将表1中的前45组样本作为模型拟合样本,以尽可能提高模型的精度;将后9组样本作为预测样本,对模型进行精度检验。
利用matlab内置nlinfit函数实现样本中前45组数据的非线性拟合,根据最小二乘估计法确定底板中心弯矩预测模型为
(4)
利用nlparci函数返回置信度为95%的参数置信区间,结果如表2所示。由表2可知,置信区间较窄,且不包含零,说明各个因素影响均不可或缺,模型较好。对该模型进行回归分析,算得均方误差为0.019 1。分析各回归参数值可知,底板厚度参数较为接近1,闸孔宽度参数为0.5左右,砂砾石地基厚度参数较为接近0,说明底板中心弯矩与底板厚度、闸孔宽度、砂砾石地基厚度的非线性程度依次递增,与前文总结的水闸各设计参数对底板中心弯矩的影响规律相符。

表1 模型样本

表2 回归参数置信区间

图7 多元非线性回归模型拟合效果对比
由式(4)计算所得底板中心弯矩值与样本值的对比如图7所示,可以看出两条曲线吻合较好。对该模型进行相关性分析,相关系数为0.934 1,说明该预测模型对数据拟合的效果较好。利用该非线性回归模型对9组预测样本进行预测,预测值及样本值对比如图8所示。由图8可知,该回归模型的预测效果较好。

图8 多元非线性回归模型预测结果拟合曲线
对多元非线性回归模型的拟合样本和预测样本计算预测绝对误差与相对误差。结果表明,54组样本的平均预测绝对误差为0.1 MN·m,平均预测相对误差为9.1%,说明模型的预测精度较高。预测样本的预测结果及误差如表3所示,可见多元非线性回归模型的预测结果与ABAQUS的计算结果较为相符,误差较小。在实际工程中,将该多元非线性回归模型的弯矩预测结果应用于配筋计算等,可以满足初步设计阶段设计人员对水闸底板弯矩的预测精度要求。

表3 预测样本的预测结果及误差
4 结 语
针对砂砾石地基上的水闸结构,将底板厚度、闸孔宽度、闸墩高度、砂砾石地基厚度4个因素作为变量,考虑闸段与闸段之间的接触效应,通过大量的有限元计算,分析了水闸参数对底板弯矩的影响规律,考虑4个因素之间的相互影响,采用多元非线性回归分析方法,建立了水闸底板中心弯矩预测模型。结果表明,底板中心弯矩与底板厚度、闸孔宽度、砂砾石地基厚度呈非线性关系,且非线性程度依次递增;底板中心弯矩与闸墩高度总体呈线性关系;所建立的预测模型相关系数较高,达到0.9以上,均方误差较小;54组样本的平均预测相对误差为9.1%,预测精度较高。整体而言,构建的砂砾石地基上的水闸底板中心弯矩多元非线性回归预测模型,较为合理地反映了各个因素对底板中心弯矩的影响,且形式简洁、便于工程应用,可将此预测模型的计算结果作为是否采取地基处理措施和施工处理措施的判断依据,也为初步设计阶段水闸底板厚度和闸孔宽度等结构设计参数的确定提供了一种新方法。
