混凝土坝服役性态监测效应量安全监控指标拟定方法

顾 昊, 曹文翰, 汪 程, 顾冲时，黄潇霏

(1.河海大学农业科学与工程学院，江苏 南京 210098; 2.河海大学水利水电学院，江苏 南京 210098；3.上海市政工程设计研究总院(集团)有限公司,上海 200092； 4.河海大学图书馆，江苏 南京 210098)

在对混凝土坝服役性态监测效应量进行安全监控指标拟定过程中，需要解决大坝服役性态评价等级属性问题[1-2]。传统的混凝土坝服役性态监测效应量安全监控指标拟定方法主要有：置信区间法、极限状态法、小概率法等[3-4]。吴中如等[5]综合小概率法和极限状态法，拟定了混凝土坝变形诊断指标；张琳琳等[6]研究了指标拟定方法并构建了指标评价体系，以医学上健康标准划分为基础，提出了大坝安全评价等级属性等区间划分法；何金平等[7]总结分析了大坝服役性态评价指标拟定规则，由此形成了一套大坝安全评价多层次指标评价体系。近年来，国内外学者除了应用和发展了传统的力学、数值解法等方法之外，将更多的新理论、新技术引入到安全监控指标拟定分析中来。Ansari等[8]定义了损伤状态矩阵，据此对混凝土坝地震后安全状态监测损伤指标进行了分类；Alembagheri等[9]以非线性增量动力分析为基础拟定了安全监控指标，分析评估了混凝土拱坝的安全状态；Shao[10]引入Copula函数，提出了考虑多测点变形相关性的大坝变形监控指标拟定方法。

上述的研究成果在大坝安全综合评价中起到了一定的作用，尤其是置信区间法及小概率法等应用较为普遍[11]，但这些方法在确定大坝服役性态评价等级属性时存在等区间划分以及监测效应量服从某一分布假定问题，影响了安全监控指标拟定精度[12]。针对上述问题，本文研究混凝土坝服役性态评价等级属性不等区间划分和评价指标量化等技术，在此基础上，探究拟定混凝土坝服役性态监测效应量安全监控指标方法，以期为混凝土坝服役性态客观评价和监测效应量监控指标有效拟定提供参考基础。

1 传统置信区间估计法拟定安全监控指标的基本原理

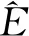
(1)

根据正态分布的对称性，式(1)等价于：

(2)

式中：Δ为置信区间半带宽；σ为标准差。

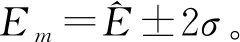
置信区间估计法运用简单，易于掌握，但存在以下不足：①若混凝土坝未遭遇过不利荷载组合或资料系列很短(不包含最不利荷载组合时的监测效应量)，则该方法只能估计混凝土坝遭遇荷载范围内的效应量，其值不一定是安全监控值;②没有联系混凝土坝失事的原因和机理，物理概念不明确；③实测值与拟合值的差值假定服从正态分布，与实际情况存在差异，影响了监控指标拟定的精度;④α的取值带有经验性，存在人为因素影响。

针对上述问题，本文综合层次分析法和灰狼智能算法，提出混凝土坝服役性态评价等级属性不等区间划分法，为拟定混凝土坝服役性态监测效应量多级监控指标提供理论基础。

2 混凝土坝服役性态评价等级属性不等区间划分方法

大量的工程实践经验可知，绝大部分混凝土坝的服役性态属于正常，因此本文基于典型小概率法，假定混凝土坝服役状态中的正常状态为大概率事件，其概率区间划分为(5%,100%]，剩余的[0%,5%]为小概率区间，当混凝土坝服役性态落在这小概率区间范围内，则表明该坝存在一定的安全隐患。基于混凝土坝的服役性态，将[0%,5%]小概率区间重新划分为4个区间，依次定义为转异、重度劣化、轻度劣化和基本正常，从而实现对混凝土坝服役性态等级属性不等区间划分。结合层次分析法与灰狼算法，提出了混凝土坝服役状态不等区间划分方法，该方法具体实现步骤如下：

步骤1构造混凝土坝服役性态除正常区间外的等级属性评语成对比较判断矩阵。

利用“转异、重度劣化、轻度劣化、基本正常、正常”5级等级属性评语来评价混凝土坝服役性态，由于等级属性评语区间的概率不确定性，因此以线性方式组成的定性术语构造除正常区间外的评语区间成对比较判断矩阵。利用S、W、O、H将1～9标度划分为4段，并记a1、a2、a3为1～9标度的截断点，则定性术语的函数关系可表示为S:[1,a1],W:(a1,a2],O:(a2,a3],H:(a3,9]，对应的评语等级属性差异性的具体划分见表1。

表1 混凝土坝服役性态等级属性评语差异性划分

在对混凝土坝服役性态除正常区间外的等级评语进行两两对比时，本文假定转异区间比重度劣化区间略微差；转异区间比轻度劣化区间明显差；转异区间比基本正常区间极度差；重度劣化区间比轻度劣化区间略微差；重度劣化区间比基本正常区间明显差；轻度劣化区间比基本正常区间略微差。依据上述假定，由此构造混凝土坝服役性态除正常区间外的等级属性评语成对比较判断矩阵为

(3)

步骤2混凝土坝服役性态除正常区间外的等级属性评语成对比较判断矩阵的一致性检验及截点确定。

在混凝土坝服役性态除正常区间外的等级属性评语划分中，需对式(3)进行一致性检验，由此确定1～9标度中截点a1、a2、a3的位置，即确定a1、a2、a3的数值大小。本文采用一致性指标CI来对式(3)进行一致性检验：

(4)

式中：n是判断矩阵的阶数；λmax是判断矩阵R的最大特征值。

为了得到式(4)判断矩阵满意的一致性，基于灰狼算法调整1～9标度中截点a1、a2、a3的位置，并对式(3)进行一致性检验，从而获取截断点a1、a2、a3的最优值。

灰狼优化算法(GWO)模拟狼群狩猎时接近、包围、攻击的步骤，建立一新型仿生智能算法模型[13-15]。狼群中任意一个个体都是一潜在的解，位于狼群顶层的3个层级的灰狼(ε，β，δ)，是3个位置最好的解，并通过这3个解判定猎物的位置，剩余的灰狼ω基于自身位置计算与猎物之间的距离，实现对猎物的狩猎。其中灰狼个体与猎物的距离为

D=|CXp(t)-X(t)|

(5)

其中C=2r1

灰狼位置更新为

X(t+1)=Xp(t)-AD

(6)

其中A=2ar2-a

a=2-2(t/max_it) (a∈[0,2])

式中：t为迭代的次数；Xp(t)为第t代猎物的位置；X(t)为第t代灰狼个体的位置；C为系数变量；A为收敛因子，当|A|>1时实行全局搜索，当|A|<1时实行局部搜索；a的取值为[0,2]；r1和r2为[0,1]内的随机数；max_it为最大迭代次数。

狼群跟踪猎物的数学模型表示为

Dε=|C1Xε(t)-X(t)|

(7)

Dβ=|C1Xβ(t)-X(t)|

(8)

Dδ=|C1Xδ(t)-X(t)|

(9)

(10)

式(7)～(9)和式(10)为狼群内个体ω与ε、β、δ的距离关系，即：

(11)

式(11)基于ε、β、δ的位置即可判断灰狼个体ω与猎物的位置关系，如此循环更新智能个体的位置，达到预定的精度停止搜索，获得最优解。综上所述，通过灰狼智能算法确定1～9标度中截点a1、a2、a3的位置。

步骤3混凝土坝服役性态除正常区间外的不等区间划分方法。

在求得混凝土坝服役性态除正常区间外的等级属性评语划分最优截点后，则可确定判断矩阵R，该矩阵在最优截点下一致性比例CI为最小值。对应λmax的特征向量为ω=(ω1,ω2,…,ωn)T，即：

Rω=λmaxω

(12)

根据式(12)即可求出该矩阵最大特征值对应的特征向量ω，将ω进行归一化处理，即可得到评语集中各评语的权重值。在[0%,5%]区间上重新划分评语集，可得到混凝土坝服役性态等级属性评价分区bi(i=1,2,3)为

V={V1,V2,V3,V4,V5}=

{转异，重度劣化，轻度劣化，基本正常，正常}=

{[0%,b1],(b1,b2],(b2,b3],(b3,5%],

(5%,100%]}={[0%,0.56%],(0.56%,1.61%],

(1.61%,3.59%],(3.59%,5%],(5%,100%]}

(13)

bi具体求解过程见下文。

3 表征混凝土坝服役性态变化的监测效应量安全监控指标拟定

通过上述方法对混凝土坝服役性态等级属性区间进行不等划分，据此拟定表征混凝土坝服役性态变化的监测效应量安全监控指标，本文基于最大熵理论来构建监测效应量概率密度函数。

最大熵理论不须提前假定监测效应量的分布概型，只要根据较少的监测效应量统计信息得到的数字特征值进行估计，就能获得精度较高的概率密度函数[16-17]，适合混凝土坝服役性态安全监控指标的拟定，下面研究反映混凝土坝服役性态监测效应量安全监控指标具体确定方法。

对于表征混凝土坝服役性态变化的监测效应量ξ的信息熵定义为

(14)

式中：f(ξ)为ξ的分布密度函数。

根据最大熵原理可知，最客观的概率密度分布是在满足根据已知样本统计信息所获得的一些约束条件下使熵H(ξ)达到最大值的分布，即：

(15)

式(15)的约束条件为

(16)

(17)

式中：R为积分空间，μi为第i阶原点矩；s为原点矩阶数。

通过伴随变分法进行求解式(17)，首先建立相应的拉格朗日方程：

(18)

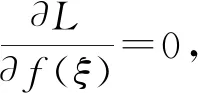
(19)

其中最重要的就是伴随算子λi的确定。将式(19)代入式(16)(17)可得：

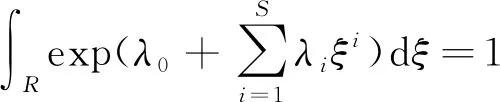
(20)

(21)

将表征混凝土坝服役性态变化的监测效应量样本数据代入式(20)(21)，求解伴随算子λi，并基于式(19)，构建最大熵概率密度函数f(ξ)，代入混凝土坝服役性态评价等级属性分区bi，则有：

(22)

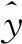
(23)

4 工程实例

某水电站是金沙江下游河段规划的最末1个梯级电站，坝址位于四川省宜宾县和云南省水富县交界处。工程以发电为主，同时改善航运条件，兼顾防洪、灌溉，并具有拦沙和对临近水电站进行反调节等作用。该工程枢纽主要由挡水建筑物、泄洪消能建筑物、冲排沙建筑物、左岸坝后引水发电系统、右岸地下引水发电系统、通航建筑物及灌溉取水口等组成，其中拦河大坝为混凝土重力坝，拦河大坝最大坝高162.0 m，坝顶长度896.26 m，该水电站正常蓄水位380.0 m，死水位370.0 m，水库总库容51.63亿m3，调节库容9.03亿m3，为不完全季调节水库。电站装机容量6 400 MW，保证出力2 009 MW，多年平均发电量307.47亿kW·h。为分析该水电站混凝土重力坝的服役性态，首先需对其服役性态评价等级属性进行划分，在此基础上，拟定该坝变形安全监控指标。

4.1 该坝服役性态评价等级属性不等区间划分

该混凝土坝服役性态评价等级属性划分为

V={V1,V2,V3,V4,V5}=

{转异，重度劣化，轻度劣化，基本正常，正常}

(24)

利用第3节中提出的方法，基于灰狼算法对截点a1、a2、a3进行调整，满足式(4)的比较判断矩阵的一致性判别，在灰狼个体位置下，随机生成600个判断矩阵R，利用这600个判断矩阵的一致性比例CI的均值作为适应度函数指标，整个迭代过程见图1。

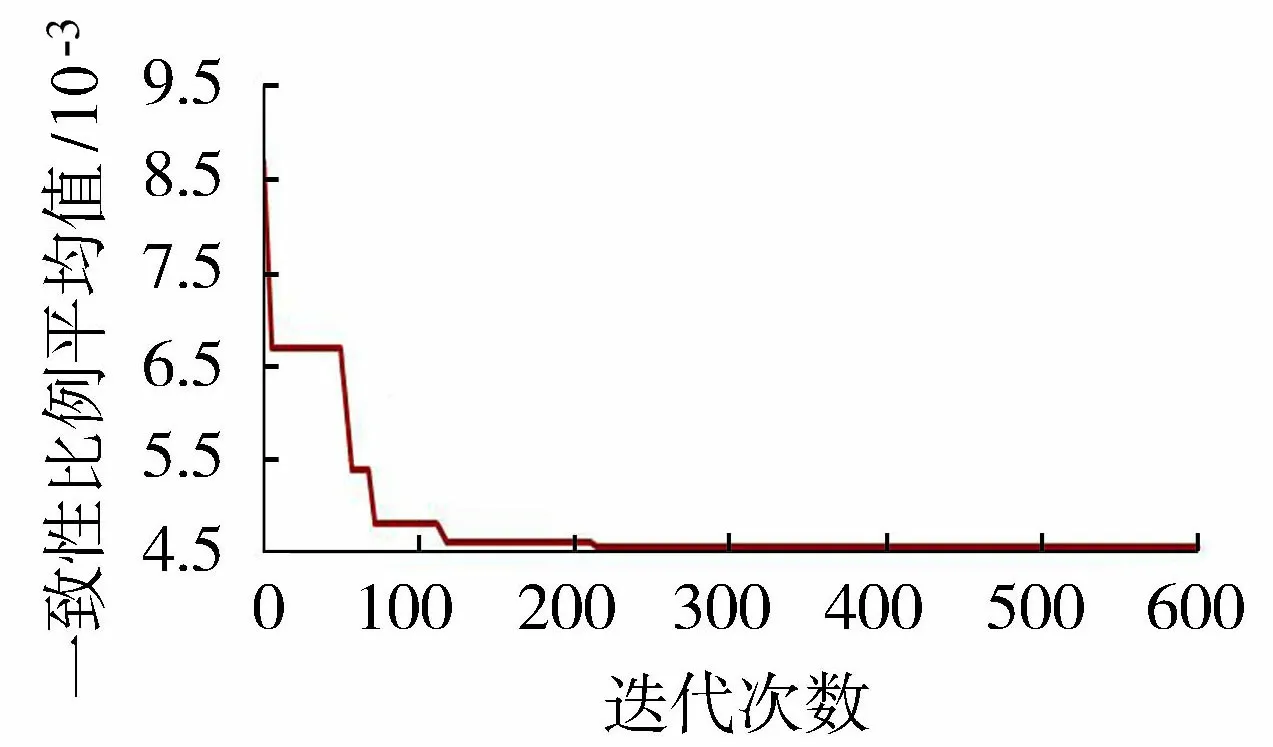
图1 适应度函数迭代过程

V={V1,V2,V3,V4,V5}=

{转异，重度劣化，轻度劣化，基本正常，正常}=

{[0%,b1],(b1,b2],(b2,b3],(b3,5%],

(5%,100%]}={[0%,0.56%],(0.56%,1.61%],

(1.61%,3.59%],(3.59%,5%],(5%,100%]}

(25)

图2 一致性比例平均值分布

4.2 该混凝土坝服役性态变形安全监控指标拟定

上述已计算得到了该坝服役性态评价等级属性划分区间，结合最大熵理论，基于式(23)确定该混凝土坝变形安全监控指标，针对该坝的具体情况，利用本文提出的方法分别建立了泄水坝段、厂房坝段、非溢流坝段1和通航坝段1坝顶水平位移安全监控指标，其代表性测点的结果见表2。

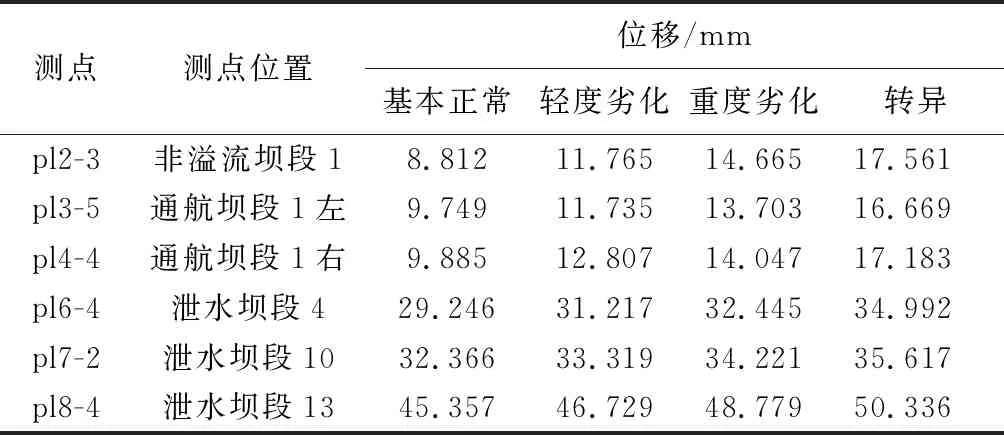
表2 典型坝段代表性测点位移安全监控指标

表2结果可知，利用本文所提出的方法确定典型位移测点的安全监控指标对应于该混凝土坝服役性态变化的不同阶段，该方法克服了置信区间法的缺陷，其监控指标拟定结果与综合反映强度和稳定不利工况组合的结构分析方法[18]拟定的结果吻合，从而验证了本文提出的方法的可行性和有效性。

5 结 论

a. 通过对传统的置信区间法拟定混凝土坝服役性态安全监控指标不足的分析，基于小概率理论，提出了混凝土坝服役性态评价等级属性不等区间划分方法，该方法以线性方式组织的定性术语，构建了混凝土坝服役性态等级属性评语间成对比较判断矩阵，以矩阵一致性比例的平均值作为适应度函数，并基于灰狼算法进行权值寻优，由此获得各评语的相对重要度，从而有效解决了混凝土坝服役性态评价等级属性不等区间划分问题。

b. 基于混凝土坝服役性态评价等级属性不等区间的划分成果，将不等区间概率值作为最大熵理论输入条件，研究了混凝土坝服役性态监测效应量概率密度函数的构建方法，据此提出了拟定对应混凝土坝服役性态不同评价等级属性的监测效应量安全监控指标，并通过工程实例验证了本文所提出的方法可行性和有效性。