考虑动态摩阻的管道泄漏水力瞬变数值模拟
2021-02-24李赟杰欧传奇刘德有
李赟杰,周 领,欧传奇,刘德有
(1.河海大学水利水电学院,江苏 南京 210098; 2.国际小水电中心,浙江 杭州 310002)
管道漏损广泛存在于流域输水、城市供水等工程中,泄漏不仅造成巨额的经济损失,而且可能造成次生灾害,如影响水质、损坏建筑基础等,因此寻求准确有效的泄漏检测方法是一个重要的研究课题。目前,泄漏检测方法主要有目视观测法、探地雷达检漏法、示踪剂检漏法、振动声学检漏法、光纤传感技术法、瞬态检漏法[1]以及稳态水力模型法等,其中,瞬态检漏法是泄漏检测的主要手段[2-3]。泄漏主要通过增加阻尼率和在产生的压力中创建新的反射信号两个方面影响瞬态信号,识别和量化这些影响是瞬态泄漏检测技术的核心[4]。
Pudar等[1]在1992年第一次提出基于压力测量的检漏程序和逆问题的解决方法,即已知压力和流量求管道粗糙度和泄漏情况。误差分析表明系统摩擦系数估计的误差带来的影响比水头测量误差的影响大得多,摩擦系数的精确性是逆瞬态法的关键[5-7]。目前,为了提高泄漏检测的精确度,除了较大泄漏问题,水力瞬变模型中一般均需要考虑动态摩阻的影响[2,8-10]。Zielke[11]推导出适用于管道瞬变层流的卷积加权模型,该模型考虑了管道瞬时平均流速和加权历史流速变化,被认为是精确动态摩阻模型;Vardy等[12-14]在Zielke[11]的基础上建立了光滑管和粗糙管内流动的瞬态摩擦加权函数模型,将卷积加权模型推广到阻力平方区;Brunone等[15]在Daily等[16]研究基础上考虑对流加速度,引入动态摩阻系数,提出了适用于层流和紊流的动态摩阻模型,该模型能很好地平衡运算量和计算精度的问题;Bergant等[17]和Vitkovsky等[18]对Brunone模型分别进行了公式改进和近似求解,使Brunone模型更加简洁、适用。郭新蕾等[3]根据实际工程需要研究了Brunone模型的离散网格和求解方法,将其应用于管道泄漏模拟,压力波形对比表明该模型比传统的准恒定泄漏摩阻模型更加精确。然而,加权函数类动态摩阻模型很少用于管道泄漏检测的研究。
本文将瞬态加速类(Brunone模型)和加权函数类(Zielke模型和Vardy模型)两类动态摩阻模型用于水力瞬变泄漏建模和模拟,并将计算结果与已有的试验数据和模拟结果进行对比,采用3种模型进行了算例计算分析,通过对比不同瞬变流模型泄漏过程中的压力和流量变化情况,分析泄漏畸变点突变原因、Brunone模型计算误差和泄漏中部分参数的敏感性。
1 动态摩阻模型
常见的动态摩阻模型主要有以下两类[10,19]:①基于加权函数考虑历史速度和历史加速度对当前流态影响的加权函数类模型,如Zielke模型和Vardy模型;②基于瞬时加速度的模型,如Brunone模型及其改进型。本文将Zielke模型、Vardy模型和Brunone模型用于管道泄漏检测的水力瞬态建模。
1.1 Zielke模型
Zielke[11]在考虑管道瞬时平均流速和加权历史流速变化的情况下,推导出了适用于层流的动态摩阻项JU:
(1)

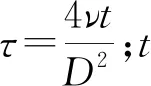
1.2 Vardy模型
Vardy等[12]建立了光滑管内流动的瞬态摩擦加权函数模型,并假定湍流黏度在均匀流速核心周围的剪切层内呈线性变化,对于高雷诺数的流动,给出了水力光滑管道动态摩阻模型:
(2)


1.3 Brunone模型及其改进型

(3)
式中:x为沿管道中心线方向的距离;a为波速;k3为Brunone动态摩阻系数,取值的适当性对模型精确程度有很大影响,k3的确定方法有两种:一是由试验确定;二是采用Vardy等[12]所给的系数公式:
(4)
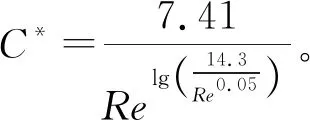
Bergant等[17]发现Brunone模型动态摩阻项计算公式具有局限性:对于某些加速或减速条件,该公式对流项符号错误,因此他们在其基础上提出了改进模型:
(5)
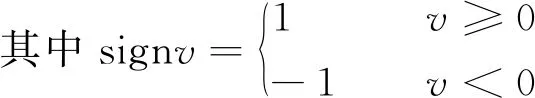
Vitkovsky等[18]随后给出了该模型的显性和隐性近似解法。
2 考虑动态摩阻的管道泄漏数学模型
管道泄漏的数学模型由控制方程、动态摩阻和边界条件3部分组成。本文采用特征线法对管道泄漏模型进行求解。动态摩阻的求解一般包含隐式和显式求解两种格式[3]:隐式求解格式中,将稳态摩阻项和动态摩阻项共同作为管道流中摩擦引起的水头损失代入双曲型微分方程,这种方法改变了特征线网格,运算复杂且求解时间长,优点是更为精确;显式求解格式中,将动态摩阻作为附加项单独计算,可以较好地代入各种模型,模型简单且计算时间短。综合考虑模型精度和运算效率,本文采用第二种方法。
2.1 控制方程
管道瞬变流的连续性方程和动量守恒方程[20-22]如下:
(6)
(7)
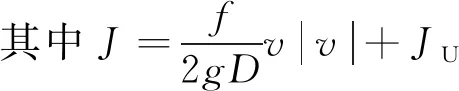
式中:H为测压管水头;J为管道水体运动摩擦引起的单位长度的水头损失;f为Darcy-Weisbach摩擦系数,其值大小依赖于雷诺数和管道相对粗糙度。
如图1所示,将线性双曲型微分方程(6)(7)变换为常微分方程,采用一阶有限差分近似,分别沿着正负特征线进行积分,得到如下C+、C-特征线方程:
(8)
(9)
式中:vP、HP分别为在t时刻节点P处的流速和水头;vR、HR分别为在t-Δt时刻节点R处的流速和水头;vS、HS分别为在t-Δt时刻节点S处的流速和水头;JR、JS分别为在t-Δt时刻节点R、S处的水头损失;Δt为计算时间间隔。

图1 特征线积分网格
2.2 边界条件
上游端为已知水位的水库,下游为一阀门,泄漏孔口边界条件如图2所示。

图2 泄漏孔边界条件
假定泄漏发生在第i个节点处,泄漏孔口外部为大气压,正负特征线测压管水头H1、H2与泄漏处测压管水头相等。由孔口出流公式得泄漏孔口的流量为
(10)
式中:Cd为泄漏孔口的流量系数,可由试验确定具体值,取值范围一般在0.60~0.61之间[23];Ag为泄漏孔口面积;ΔHL为泄漏点的压力水头,ΔHL=HL-zL,其中HL为管道泄漏处的测压管水头,zL为管道泄漏点高程。
由连续性方程可得:
Q1=Q2+QL
(11)
式中:Q1、Q2分别为泄漏节点处的正向特征线和负向特征线对应的流量。将式(10)(11)与式(8)(9)联立求解,可得流量Q1、Q2、QL和测压管水头H1、H2、HL。
3 模型验证
3.1 无泄漏纯水锤情况
不考虑泄漏情况,将本文动态摩阻模型(Zielke模型、Vardy模型和Brunone模型)的模拟结果与Bergant等[17]的实测数据进行对比。试验装置基本参数如下:管道长L=37.23 m,直径D=0.022 1 m,上游水箱恒定水头h=32 m,波速a=1 319 m/s,管道初始流速v0=0.3 m/s,雷诺数Re=5 600。阀门瞬间关闭,模拟的阀门处压力(用测压管水头Hv表示)如图3所示。由图3可知,与不考虑动态摩阻的传统摩阻模型相比,动态摩阻模型能精准描述瞬变管道压力幅值和衰减,随着周期数增加,动态摩阻模型的模拟值与实测值仍能吻合较好,而传统摩阻模型模拟的压力波在两个周期后误差逐渐增大,相位偏移加大。

图3 不同摩阻模型模拟的阀门处测压管水头与实测值对比
3.2 存在泄漏情况
考虑管道泄漏情况,将本文模拟结果与Lee等[24]模拟的结果进行对比,其模拟参数为:L=2 000 m,波速a=1 000 m/s,D=0.5 m,h=50 m,初始管道流量Q0=0.02 m3/s,Re=50 000,f=0.02,泄漏孔口距上游水库300 m,初始泄漏量QL=0.2Q0。不考虑动态摩阻的影响,模拟结果见图4。从图4可以看出,两次模拟的压力幅值和衰减几乎完全一致,从而证明了本文模型的正确性。

图4 泄漏情况下阀门处压力对比
4 算例分析
如图5所示,选择水库-管道-阀门(RPV)模型进行管道泄漏瞬变模拟。假定管道为一水平直管,模型参数为:L=2 000 m,D=0.2 m,上游水库水位恒定为60 m,a=1 000 m/s,Q0=0.02 m3/s,Re=85 000,f=0.03。

图5 泄漏管道概化物理模型
4.1 畸变点分析
假设泄漏孔外界为大气压强,泄漏位置(距上游水库的距离)XL=1 000 m,QL=0.1Q0。节点数N=100,t=0时末端阀门瞬间关闭,计算时间为32 s,分别模拟了该泄漏情况下的阀门处压力Hv和管道入口处流量Q,结果如图6所示。
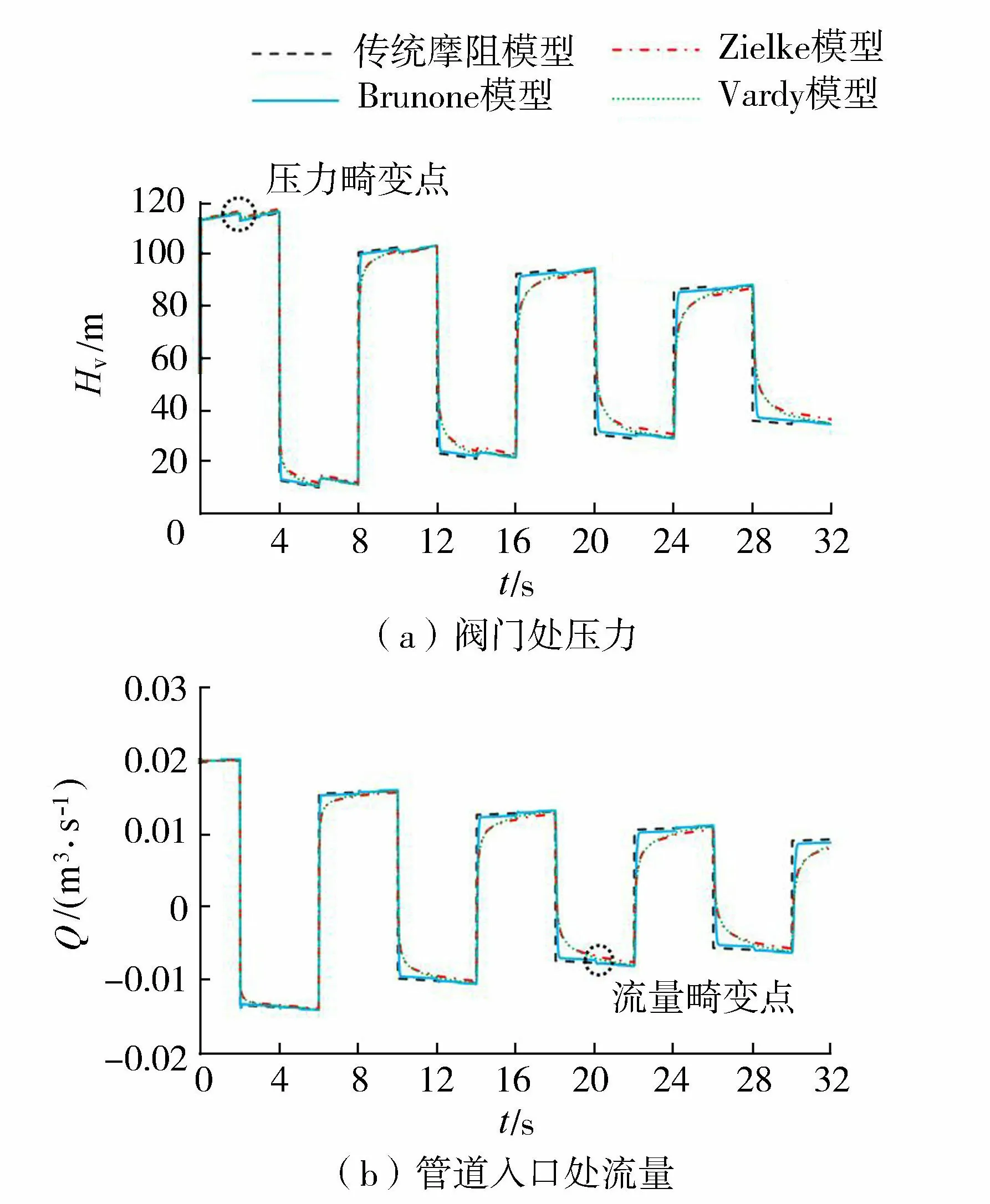
图6 有泄漏时不同摩阻模型模拟的阀门处压力和管道入口处流量
由图6可知,管道出现泄漏时,管中压力和流量会出现畸变。相比于流量,压力畸变更加容易观察,因此使用压力畸变信号能更好地探寻泄漏点。
以泄漏时阀门处的压力变化为例,阀门关闭前,管道中水体处于恒定流状态,水库水位保持恒定,压强为p0,当阀门突然关闭时,紧靠阀门处的水体流速瞬间变为零,压强立刻升高Δp,上游水体碰到静止不动的水体时就像碰到完全关闭的阀门一样,类似状态以波速a向上游传播,这种波称为主压力波,主压力波对管道压力和流量变化起主要作用。当主压力波到达泄漏点时,泄漏处的压力发生突然变化,在泄漏点形成向泄漏两侧传播的次压力波,次压力波也会影响管道压力变化。图7给出了管道泄漏时该工况下不同时刻的压力波运动图形。
由图7(a)可知t=2 s时阀门处压力畸变的原因为:主压力波从阀门向上游传播,经过泄漏点时形成新的次压力波。主压力波从阀门传递至泄漏点前引起水体压力增大,当这种增压波遇到泄漏点(假定为大气压)时,由于压差作用会向阀门处反射一个引起水体压力减小的减压信号,在t=2 s时到达阀门,引起阀门处压力突降。

图7 泄漏时不同时刻管道的压力波运动
由图7(b)可知t=4 s时阀门处压力骤降的原因为:增压波从阀门向水库传播,引起逐段的水体压力增大,传播至泄漏点时,不仅有向阀门处的减压波,也会产生向水库方向的次压波,这种波也为减压波。由于主压力波起主导作用,主增压波和次减压波叠加仍然会使泄漏点上游的管道压力增加,传播至水库时,由于压力差Δp的作用,水库向阀门反射一个使下游压力降低的波,在t= 3 s时又到达泄漏处产生新的次波,此时仍有从泄漏点反射的其他次波,同样的叠加作用使得泄漏点下游管道压力降低,t= 4 s时到达阀门导致阀门处压力骤降。
4.2 Brunone模型计算误差分析
Zielke模型主要适用于层流,也可用于雷诺数不高(Re<106)的湍流;Vardy水力光滑管道动态摩阻模型[12]适合于湍流情况,Vardy改进模型[13]给出了雷诺数在2×103~108情况下更为精确的系数计算公式;Brunone模型在层流和紊流时均可适用。Zielke模型和Vardy模型通常被认为是精确动态摩阻模型,Brunone模型有简化,存在一定的简化误差[25]。在XL=1 000 m,QL=0.1Q0工况下得到压力如图8所示,其中图8(a)为3种动态摩阻模型模拟的阀门处实际压力对比,图8(b)是以Vardy模型为标准,3种模型模拟的阀门处的压力分别减去Vardy模型的模拟值所得到的压力对比曲线。

图8 不同动态摩阻模型模拟的泄漏时阀门处压力对比曲线
由图8(a)可知,Brunone模型在前半个周期内所模拟的压力幅值和衰减与Zielke模型、Vardy模型基本一致,随着时间增长,因泄漏导致的压力畸变值虽趋于一致,但其整体压力衰减值小于Zielke模型和Vardy模型,两个周期后的压力曲线与Zielke模型和Vardy模型产生明显差异。图8(b)可以更好地印证图8(a)中所观察到的现象,Brunone模型在t=4 s时开始与Zielke模型和Vardy模型产生明显偏离,偏离值随时间增长而增大,并每隔半个周期出现一次较大的异变点,Zielke模型和Vardy模型在图8(a)(b)中均无明显差异。可能的原因是简化的Brunone模型有一定的模型误差,Brunone模型的系数k3对模型的精确程度有较大影响,需要现场率定。
4.3 参数敏感性分析

图9 不同泄漏量影响下的管道压力、流量变化
以Vardy模型为例,考虑泄漏模型在不同泄漏量和不同泄漏位置情况下的管道压力、流量变化。模型参数不变,泄漏位置距上游水库1 000 m,初始泄漏量QL分别取0.01Q0、0.05Q0、0.1Q0和0.2Q0,图9比较了4种工况下阀门处压力Hv、泄漏处压力HL、管道入口处流量Q和泄漏处流量Q1。由图9可见,初始泄漏量越大,阀门起始压力越小,这可由水锤基本公式验证。随着泄漏量增加,压力和流量阻尼增大,收敛速度加快,压力畸变点随着泄漏量增加变得越来越清晰,畸变量与初始泄漏量呈正相关,与时间呈负相关。
为了分析不同泄漏位置情况下的管道压力、流量变化,固定QL=0.1Q0不变,泄漏位置XL分别取距上游水库500 m、1 000 m、1 500 m,模拟结果如图10所示。由图10可知,不同泄漏位置会导致压力和流量畸变点位置变化,以阀门压力第一周期为例,泄漏点越靠近阀门,畸变越早,畸变时间基本与泄漏距阀门距离成正比,据此可根据畸变时间反推泄漏位置,其他压力和流量畸变情况类似,可由压力波运动情况推得;泄漏量相同,泄漏位置不同时压力和流量的幅值不同,阻尼不同,泄漏位置越靠近阀门,压力和流量曲线幅值越小,衰减越快。
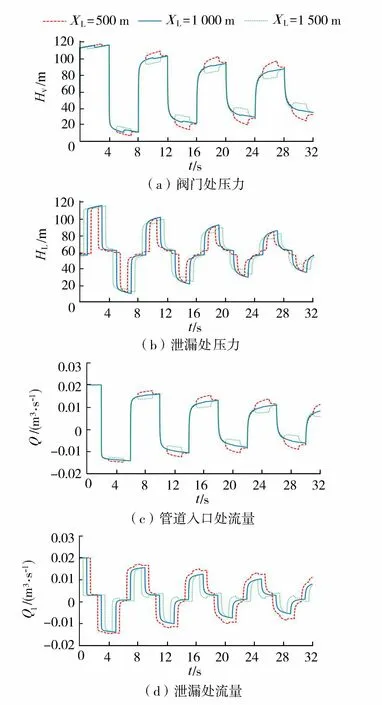
图10 不同泄漏位置影响下的管道压力、流量变化
5 结 论
a. 动态摩阻模型比传统准恒定摩阻模型更加精确,能更好地模拟管道泄漏时管中各点的压力和流量变化。与Zielke和Vardy动态摩阻模型相比,Brunone模型存在一定的简化误差,模型系数须现场率定。
b. 与流量畸变信号相比,在管道中用压力畸变信号探寻泄漏点更加方便快捷。泄漏参数敏感性分析发现,管道泄漏量与泄漏位置均对管道压力和流量信号产生影响。
