基于原型观测的输水渠道糙率取值及变化分析
2021-02-24张雨山王双银臧聪敏尚毅梓白云岗
张雨山,王双银,臧聪敏,尚毅梓,白云岗
(1.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100;2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京 100038;3.新疆水利水电科学研究院,新疆 乌鲁木齐 830000)
长距离输水工程对区域经济发展和受水区城市建设具有重要战略意义,糙率作为衡量水头损失的重要参数,其取值的合理直接影响渠道的调度和输水。长距离渠道的过流能力受断面、衬砌面粗糙程度、底坡等多方面影响而呈现不确定性[1],糙率存在较大的变化范围,而水面线对糙率的变化较为敏感[2],现有的经验取值和公式计算存在较大误差[3],难以满足渠道水力计算的要求[4]。
目前国内混凝土渠道的原型观测糙率在0.011~0.019之间[5-6],对于长距离渠道,其沿程糙率分布不均匀。原型观测数据只针对具体断面[7-8],且缺少基于长期观测数据的糙率分析[9],而水力计算中采用的糙率通常为渠段乃至渠道的综合糙率[10]。为此,本文以北疆输水工程总干渠为研究对象,在对2011—2016年断面观测数据统计分析的基础上,采用非恒定流数学模型,分段率定渠道糙率,通过模拟值与实测值的时、空间对比,对总干渠糙率取值及糙率修正因子进行了定量分析,为该工程的糙率取值和工程管理维护提供依据,并为同类型渠道提供参考。
1 研究方法
1.1 糙率计算公式
在阻力平方区,谢才-曼宁公式是计算糙率的水力学基本公式[11],因其计算的稳定性,被广泛应用于河渠的糙率计算中。计算公式为
(1)
式中:n为糙率;Rw为水力半径;A为断面面积;Q为流量;J为水力坡度。
对于梯形断面渠道,水力半径计算式为
(2)
式中:b为渠道底宽;h为水深;m为边坡系数。
美国垦务局和陆军兵团根据实测资料和试验分析提出了形式相近的混凝土渠道糙率经验公式[12],其区别在于美国垦务局公式将描述边壁不平整度的等效粗糙度Ks作为定值取0.001 25,而美国陆军兵团公式将Ks作为变量处理[13];工程中常将粗糙特征类似的表面糙率当作统一常数,采用经验进行取值,Cowan等[14-16]根据已有工程的经验总结,将渠段糙率的影响因素分为不同单元,在确定顺直、光滑渠段糙率的基础上,再计算不同因素的影响值。计算式为
nc=a(nb+n1+n2+n3+n4)
(3)
式中:nc为渠段综合糙率;nb为顺直、断面完好渠段的糙率基准值,通常作为渠道糙率的取值下限;n1、n2、n3、n4分别为渠道表面不规则度、断面变化、渠道内阻水物、渠道生物附着对糙率的影响值;a为弯曲渠段的弯度校正因子。
1.2 非恒定流数学模型
圣维南方程组是一维非恒定渐变流的基本方程[17],由连续方程和动量守恒方程组成,方程为
(4)
式中:q为侧向入流;C为谢才系数;g为重力加速度;x为计算距离;t为时间。
为了完整地实现长距离渠道全输水期的工况模拟,采用稳定性较高的Abbott六点隐式差分法对圣维南方程组进行离散,利用追赶法求解。节点按照水位、流量、水位交替布置,提高了模型计算稳定性,可在较大的克朗数下保持收敛。糙率系数由明渠恒定流的谢才-曼宁公式计算,参与一维非恒定流的计算[18],R作为曼宁糙率的重要变量,采用过水断面面积与湿周的比值所定义的有效水力半径。
1.3 精度评价
采用定量评估法评价模型精度,采用均方根误差(RMSE)ERMS衡量模拟值与实测值之间的实际偏差,平均绝对百分误差(MAPE)EMAP衡量相对偏差,采用R值评价拟合度,计算公式为
(5)
(6)
(7)
式中:na为系列长度;Xr为实测值;Xm为模拟值。
1.4 单因素敏感度
采用单因素敏感性分析的方法计算渠道水面线对水力参数变化的敏感度:
(8)
式中:S为敏感度;Δα/α为水力参数的相对变幅;Δm/m为水面线的相对变幅。当S≤0.05时表示该指标不敏感,当0.05
2 工程概况及数据
2.1 渠道概况
北疆输水工程于2000年建成运行,2016年渠首引水达到7.12亿m3,最大引水流量达到96.7 m3/s。工程地处寒温带,每年输水期为4月27日至9月16日,冬季停水期均存在冻融循环,最大冻土深度为1.5 m。其中总干渠全长约130 km,设计输水流量68 m3/s,均采用混凝土预制板衬砌,表面无明显生物附着,水质为地表水III类以上,含沙量较低,泥沙运移影响可忽略。工程投入运行时间较长,衬砌板面受水流冲刷出现不同程度的麻面,受地质和环境情况的影响(冻胀和地基不均匀沉降等),不同渠段的边壁平整度也有一定差异。
2.2 原型观测
自渠首2 km至130 km处选择4个观测断面作为典型断面,间隔在20~30 km,断面位于距渠系建筑物较远的顺直渠段,断面结构完整且水流较为平稳。在渠道上方布置测桥进行观测,采用流速面积法测流,测速垂线间隔为1 m,测流历时在60~100 s,得到渠道自4月开闸引水至9月关闸的逐日水位、流量数据,时间跨度为2011—2016年(2013年缺测),观测渠道基本参数见表1。

表1 典型断面基本参数
2.3 实测数据数理统计
采用式(1)反算各断面的逐日糙率值,由于断面的水位、流量数据是基于同一地点的重复测验,初步判断糙率系列具有正态性。将各断面糙率系列进行正态分布拟合,结果表明各输水期的糙率系列均服从正态分布,限于篇幅仅列出2+990断面2016年的糙率正态拟合如图1所示。将各断面不同输水期的糙率系列正态拟合后的期望值与标准差统计如表2所示。
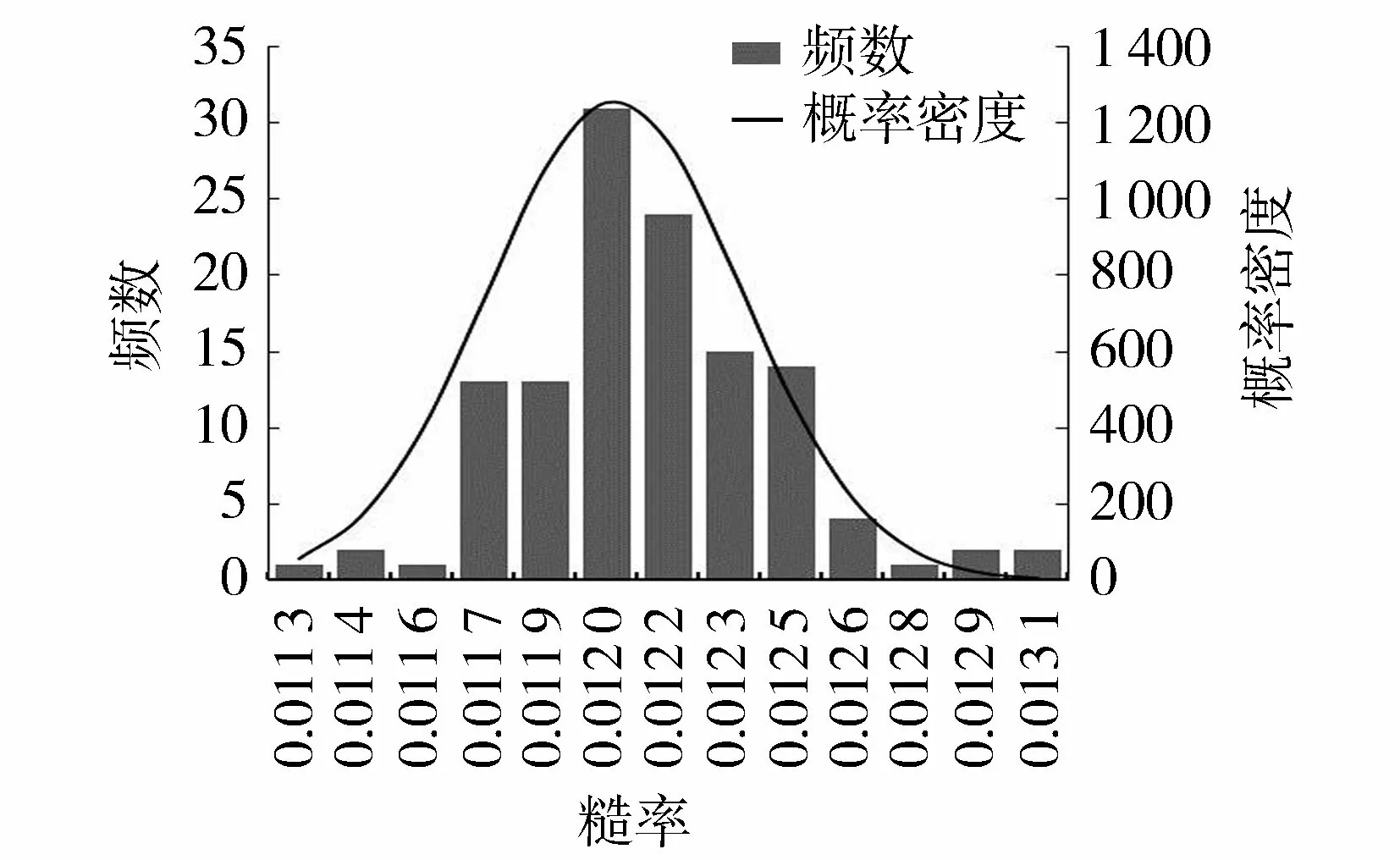
图1 断面糙率正态分布拟合

表2 典型断面输水期糙率期望值与标准差
3 数学模型
3.1 模型构建
选取总干渠0+000~57+300区段为研究段,为反映渠道实际情况,通过Google earth绘制带有坐标的渠道底图,采用分段率定的方法率定糙率[20],根据沿线的建筑物和弯道情况,将研究段分为渠段1(0+000~9+185)、渠段2(9+185~48+000)和渠段3(48+000~57+300),概化渠道如图2所示。

图2 研究段渠线布置
模型边界条件设置上,上游边界为进水口实测流量过程,下游边界为渠段末实测水位过程,内部边界为分水口实测流量过程;模型计算上,为满足最大计算距离大于建筑物前后断面长度且克朗数小于10,最大计算距离取2 000 m,模拟时间步长选择5 min。与实际观测频率相同逐日输出结果,通过迭代率定渠段糙率[21],流程如图3。

图3 模型糙率率定流程
3.2 参数取值及敏感性分析
模拟渠段的基本水力参数包括渠段糙率、闸门收缩系数和局部水头损失系数,采用Cowan[14]提出的基准值修正的方法,以顺直段原型观测结果为取值下限,根据弯道情况,以弯度校正因子a=1.5为取值上限。由于渠道无明显附着物,且单个渠段内断面一致,其余影响值可忽略,即渠段糙率取值区间为[n,1.5n];节制闸在稳定输水期处于全开状态,自由出流情况下收缩系数只与断面形式有关,建筑物进、出口水头损失计算采用式(9)计算,并以模型推荐值的最小值作为取值下限,闸门收缩系数根据模型参考取值区间,各参数取值区间见表3。
(9)
式中:As1、As2分别为建筑物进口和出口断面面积;A1、A2分别为建筑物前、后渠道断面面积;常数ζin=0.5、ζout=1.0。
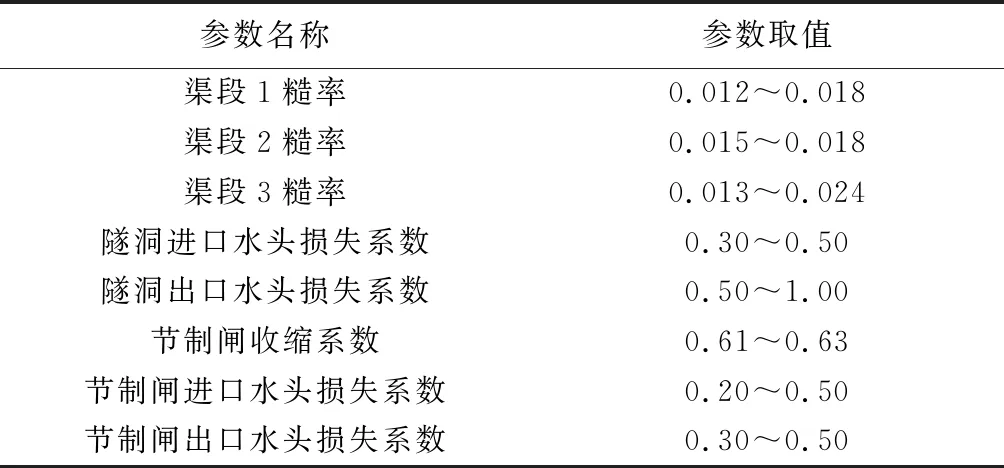
表3 参数取值范围
采用单因素敏感性分析法计算渠道水面线对糙率、闸门收缩系数Uc和建筑物水头损失系数变化的敏感度S。在保持其他水力参数取值不变的情况下,糙率取值及对应渠道断面水位变化如表4所示。上游2+940断面渠道水深对糙率变化的敏感度为0.21;下游49+270断面的敏感度为0.27,表明渠道水位对沿程糙率的敏感度指标为敏感,糙率每上升0.002,渠道水位约有0.10~0.15 m的抬升,且不同位置的敏感度有差异。

表4 不同糙率变幅下渠道水深变化
对建筑物进、出口水头损失系数及闸门收缩系数同样采用控制变量的方式分析其敏感度,渠道水深对建筑物进出口水头损失系数敏感度为0.010~0.012,对闸门收缩系数敏感度为0.003~0.004,均表现为不敏感。由敏感性分析可知,在水动力模型中,渠道水位对沿程糙率的变化表现最为敏感,通过拟合实测水位过程与模拟水位过程的方法可以较精准地率定渠段糙率。
3.3 模型率定
对渠道水位和流量过程进行数学模拟,按照弯道和过水建筑物的分布,将渠道分为3个渠段进行分析,选取2016年各渠段对应的典型断面实测逐时水位资料,分别对各段参数进行率定。通过对糙率在内的各参数试调[22],明确各参数对水流计算的影响,使各断面的模拟水位过程与实测水位过程相符,使模型可以反映渠道真实的水流过程,并依此确定水力参数取值。其中2016年输水期典型断面的拟合情况如图4所示。
3.4 精度评价

图4 典型断面模拟与实测水位过程拟合
将边界条件替换为2011—2015年的实测数据,采用研究段上、下游典型断面作为控制断面,对模型进行验证。分别采用RMSE和MAPE评价模拟值和实测值的偏差情况,采用R值评价二者的相关性,对各年输水期模拟结果精度进行评价,结果如表5所示。ERMS在6 cm以内,EMAP在1.08%以内,R值在0.925以上,表明模拟值和实测值拟合度较高,模型能反映目标渠道的实际水流特征,其率定的水力参数可靠。
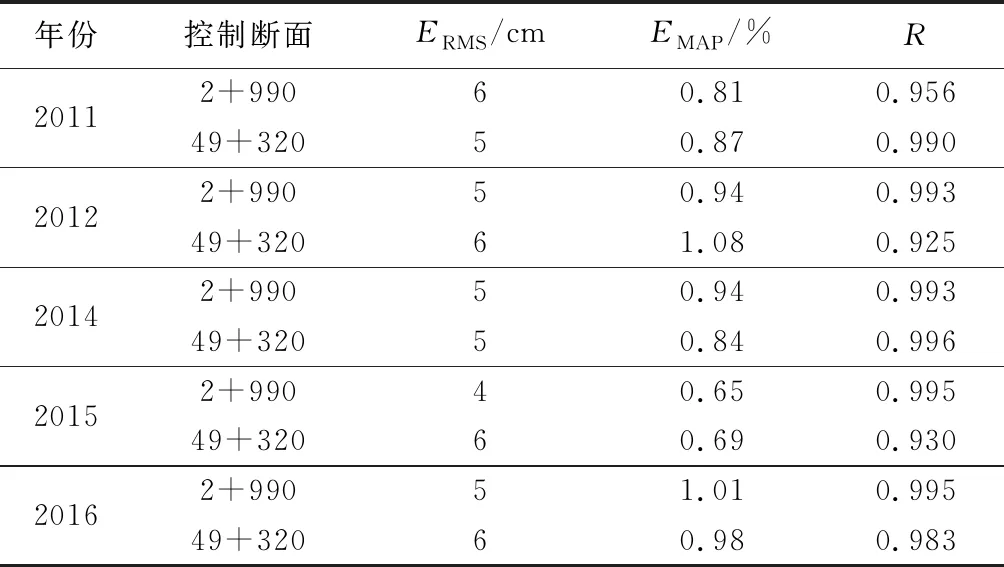
表5 模型精度评价
4 结果分析
4.1 渠段糙率特征
将渠段糙率与实测典型断面糙率对比如表6,根据工程采用糙率精度,取两位有效数字,计算典型断面糙率与渠段糙率的比值。
数学模型计算采用的为渠段综合糙率nc,原型观测为渠道顺直部分的断面糙率nb,由于各渠段内的断面一致,且无明显边壁附着,式(3)可以写为nc=anb。在无明显弯道的渠段2,a=1.00~1.07,nb=0.015~0.016,表明典型断面的实测值可以代表顺直渠段的综合糙率;渠段1由于存在较明显的弯道,a=1.15~1.25,而在弯道较复杂的渠段3,a=1.46~1.54。渠段2实际渠长和首尾直线距离的比值为1.12,而渠段3的比值为1.56,表明弯道对渠段综合糙率有较大的影响,且弯度校正因子的大小与弯道复杂程度呈正相关关系。

表6 渠段及断面糙率对比
4.2 年际特征
根据原型观测结果(表2),糙率随时间存在一定变幅,典型断面糙率在6年间整体呈上升趋势,变幅在7%~12%。为排除其他因素影响,选择能代表顺直渠段综合糙率的20+000断面,其糙率随年际变化如图5所示,线性拟合的糙率年增幅为0.000 28。
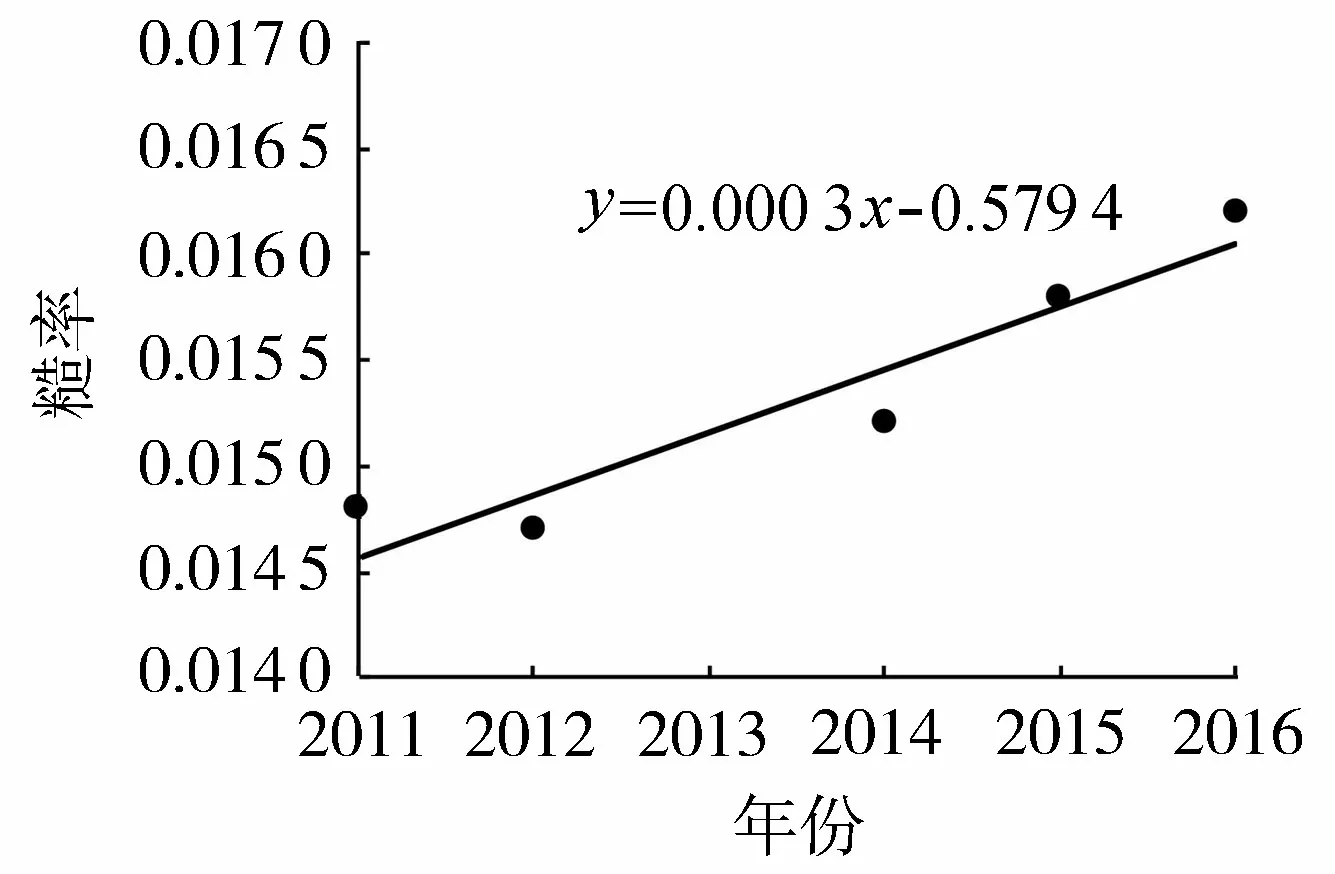
图5 20+000断面糙率年际变化
除去进行翻新的渠段1,渠段2、渠段3的综合糙率在6年间的增幅分别为1.1%与9.4%,与断面实测糙率变幅基本相符。弯道渠段糙率增幅大于顺直段,表明在断面与衬砌情况一致的条件下,弯道段的水流冲刷情况相较于顺直段更为严重,是工程需要重点维护的渠段。在不同运行时期或衬砌维护水平较差的情况下,渠段糙率的增大需要重视。
北疆输水工程水质条件较好且几乎没有生物附着存在,对长期运行下的渠道糙率影响较小,对于含沙量低且定期清淤的渠道,不易产生长期淤积,糙率增长的主要原因是边壁平整度的变化。根据渠道的运行记录,存在影响衬砌面的因素有衬砌面的老化脱落,渠底和边壁的鼓胀、裂缝等,而2016年自渠首向下进行的5 km衬砌面翻新使2+990断面糙率相较于上一年减小了约8.4%,表明在断面形式不变的情况下,渠道边壁情况是渠段糙率的主要影响因素,高寒地区的冻融循环和不稳定的基岩导致的衬砌老化与渠道不平整是渠道维护面临的主要问题。
为量化边壁粗糙程度的影响,选取将边壁等效粗糙度Ks作为变量的美陆军兵团公式,采用最小二乘法[23]率定Ks,使经验公式计算值与实测数据的偏差最小,计算公式为
(10)
式中:Ri为对应水力半径;ni为实测糙率。
与糙率趋势相同,各渠段Ks的年增长率如表7所示。根据各渠段长度的加权平均,北疆输水工程总干渠的Ks年增长率为18.54%,其中2016年渠段1翻新后的初始Ks值为0.000 15。
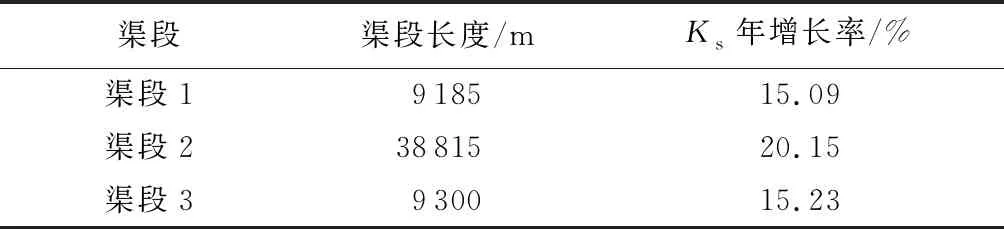
表7 等效粗糙度增长率
根据混凝土渠道运行经验,渠道糙率随时间增长,20~30 a达到一个较稳定水平[12],根据Ks的增幅和投入运行时间,总干渠处于中期运行水平,在不进行类似衬砌面翻新和大面积维修的情况下,北疆渠道Ks远期可取0.001 3~0.001 9。总干渠糙率在远期运行水平预期可达0.018~0.022,将超过0.017的渠道设计糙率,为保证渠道的稳定输水,对衬砌老化严重渠段的翻新工作十分必要。
5 结 论
a. 北疆输水工程总干渠水动力模型中,糙率取值每增加0.002,渠道水位约有0.10~0.15 m的抬升,为敏感参数,MIKE11模型可以在较短时间,通过典型断面实测流量、水位数据对长距离渠道不同段的渠段综合糙率进行率定,在使用实测资料计算的同时避免了单一断面观测对长距离渠道糙率取值的局限性。
b. 北疆渠道顺直段糙率取值在0.015~0.016,糙率受边壁粗糙程度和弯道的影响明显,弯道段的弯度校正因子取值在1.15~1.5,且与弯道复杂程度呈正相关;总干渠新衬砌渠段的Ks可取0.000 15,无维修、清淤情况下,总干渠Ks年增长率在18.54%,渠道边壁粗糙程度随时间的变化与渠道衬砌材质、水流冲刷、混凝土老化等因素有关,不同渠道甚至不同渠段的Ks增幅存在一定差异,不进行衬砌维护的情况下渠道糙率在远期运行水平预计会超过设计值。
