中国区域平均降水量序列构建方法比较研究

战云健 任国玉 王朋岭 潘旸 张雷 孙秀宝

1 国家气象信息中心，北京 100081

2 国家气候中心，北京 100081

3 中国地质大学环境学院大气科学系，武汉 430074

4 中国科学院南海海洋研究所热带海洋环境国家重点实验室，广州 510301

1 引言

降水作为重要的气象要素，是否存在大范围、长时间的变化，对人类活动影响重大，同时也是气候变化检测和归因研究的重要内容。20世纪70年代之前对降水的观测，基本只有地面台站观测。其观测误差小，准确性好，时间序列长，适用于年代际降水变化分析工作。然而，由于降水的局地性强，时空分布均不连续（Ison et al., 1971; Jamaludin and Jemain, 2007; Liang et al., 2012），雨量器观测得到的降水量记录不能代表面雨量（任芝花等, 2003; 徐晶和姚学祥, 2007），需要进行区域平均计算来获取面雨量序列。在全球和中国区域，地面降水观测台站空间分布不均匀，较为干燥的地区和高山高原地区，台站一般较为稀疏，导致不同计算方案所得区域平均降水序列的多年平均值和变化趋势特征具备明显差异，是降水变化研究结论不确定性的一个重要来源（Vose and Menne, 2004; Wan et al., 2013;任国玉等, 2015）。

常用的区域平均降水量时间序列计算方法有：所有台站直接求算术平均、经纬度网格面积加权平均方法（Jones, 1994; Jones and Hulme, 1996）、泰森多边形法（Thiessen, 1911）、通过克里金（Oliver and Webster, 1990）等插值方法将站点插值成格点产品再求平均、现行中国气候监测业务中的“省面积加权平均方法”等，本质都是把位于不同地区的站点赋予不同的权重进行平均计算。在面积较小、台站数目不多的区域，多采用直接求平均的方法计算，相当于全部台站的权重系数均一致。泰森多边形法、克里金插值等插值方法中每个台站的权重取决于其与周围台站之间的距离（方慈安等, 2003; 颜真梅和母国宏, 2017），对于江河流域面雨量的计算效果较为理想，但由于其在台站稀疏区域的站点权重会异常偏大，很少用于大尺度区域平均降水计算。

若站点数量较多、研究范围大，经纬度网格面积加权平均方法可以在一定程度上消除台站空间密度不均匀引起的问题，前人多采用5.0°（纬度）×5.0°（经度）（施能等, 2004; Wan et al., 2015）、2.5°（纬度）×2.5°（经度）（任国玉等, 2005），2.0°（纬度）×2.0°（经度）（Zhai et al., 2005; 任国玉等,2015）或其他（Donat et al., 2016）不同尺度的矩形网格构建大范围的平均降水序列。省面积加权平均方法利用中国区域各省的准确面积来加权计算区域平均值，用于中国气候变化监测业务。总之，在中国区域平均降水量计算工作中，站点直接平均、不同网格大小的经纬度网格面积加权平均方法、省面积加权平均方法应用较多。这些方法具有各自的优缺点和适用性（表1），但由于缺少区域降水真值，先前对方法的选择取决于主观认定，未能客观定量比较不同方法所得区域平均降水序列的准确性。

近年来，降水观测技术不断发展，开始有天气雷达观测、卫星监测等降水观测手段。雷达观测降水的时空分辨率高，但会受到电子信号以及运行环境等多种误差来源的影响，导致测量出现偏差（van de Beek et al., 2010）。卫星反演降水资料观测范围广、时间间隔短，时空分布连续，对年降水量的估计值接近于实际，但其对降水强度的估计误差较大（Shen et al., 2010; 宇婧婧等, 2013）。通过多种最优插值方法（潘旸等, 2012）、概率密度匹配法（宇宇婧婧等, 2013）等技术手段对降水观测资料进行融合，结合各种降水观测手段的优点，获取了时空分布均匀且在中国范围内无缺测的多源融合降水格点产品，对年降水量的估计准确性高（宇婧婧等, 2015;陈圆圆等, 2016），该产品的区域平均值基本不受计算方法的影响。然而，其序列长度较短，无法用于中国地区几十年尺度的气候变化监测业务和研究工作。

本文利用1998～2012年中国地区多源融合降水产品的区域平均降水量序列作为“参照值”，通过定量比较1998～2012年直接求平均、不同尺度的经纬度网格面积加权平均、省面积加权平均等方法所得降水量序列与参照值序列统计属性的差异大小，判断各方法所得序列的准确性。

表1 不同区域平均方法的优点和缺点理论分析Table 1 Theoretical analysis of the pros and cons of the average method in different regions

2 资料与方法

本文所用资料为国家气象信息中心提供的中国地面2425站日值降水数据集（以下简称站点数据集）以及中国地面与CMORPH（CPC Morphing Technique）融合逐日0.25°（纬度）×0.25°（经度）分辨率降水产品（CMPA_Daily V1.0，以下简称格点数据集）。其中站点数据集的起始时间是1951年，终止时间为2016年。格点数据集的起始时间是1998年，终止时间为2012年。选取（15.0°N～55.0°N，75.0°E～135.0°E）这个矩形区域内的中国大陆地区为研究范围，格点数据集的全部时段1998～2012年作为研究时段，该时段内的站点数据均已通过质控系统的自动检查和人工订正，基本不存在错误数据，只有极少量的“疑误”数据（任芝花等, 2015）。本文将全部“疑误”数据修改为缺测，以消除数据准确性问题引起区域平均序列偏差的可能性。

为避免站点数据的完整性差异对区域降水量估计产生影响，将缺测较多的台站排除。在研究时段（1998～2012年）内，如果某站某年任意1个月的总缺测日（包含“疑误”数据转化来的缺测日）达到或超过3 d，则该年记为缺测。选取了研究时段内至少有12个不缺测年（占研究时段的80%）总共2377个站（图1a）。虽然可以允许台站最多存在3年的缺测记录，但实际只有0.208%的台站缺少1或2年记录，其余台站记录完整。因此，认为区域平均序列受缺测数据的影响可以忽略不计。

格点数据集在中国区域内的全部网格（图1b）均无缺失，其中国区域平均年降水量（以下简称参照值）接近实际值。由于站点数据也可认为不存在时间完整性问题和准确性问题，不同方法所得区域平均序列的不确定性只来自于降水观测台站的空间密度差异，其与参照值的差异越小则区域平均效果越理想。由于100°E以东的台站密度明显大于100°E以西。以此为界划分中国西部和中国东部，也分别计算区域平均序列，代表了台站空间密度较高和较低两种情形。

降水量距平、距平百分率、标准化距平亦是分析降水变化特征的重要指标（任国玉等, 2015; 战云健等, 2019），在每个台站和参照值网格上，计算研究时段内每年的总降水量及降水量距平、距平百分率、标准化距平。其中，降水量距平的单位和降水量原始值一样，为mm，降水量距平百分率的单位是%，标准化距平是无量纲单位。

得到每个台站或格点每年的年降水量以及几种距平指标之后，采用不同区域平均方法计算全国以及中国东部、中国西部的区域平均时间序列。经纬度网格面积加权平均方法（Jones and Hulme, 1996）的计算步骤如下：首先，把中国范围按经纬度划分为 0.25°×0.25°（0.25°网格）、1.0°×1.0°（1.0°网格）、2.5°×2.5°（2.5°网格）、5.0°×5.0°（5.0°网格）、10°×10°（10°网格）5 种不同尺度的经纬度网格（图1c–1f，0.25°网格图略）；然后，计算每个网格内所有站点的算术平均值；最后，根据网格中心点纬度加权计算得到区域平均序列。其中，如果某网格为空 网格，则该网格不参与计算。计算公式为

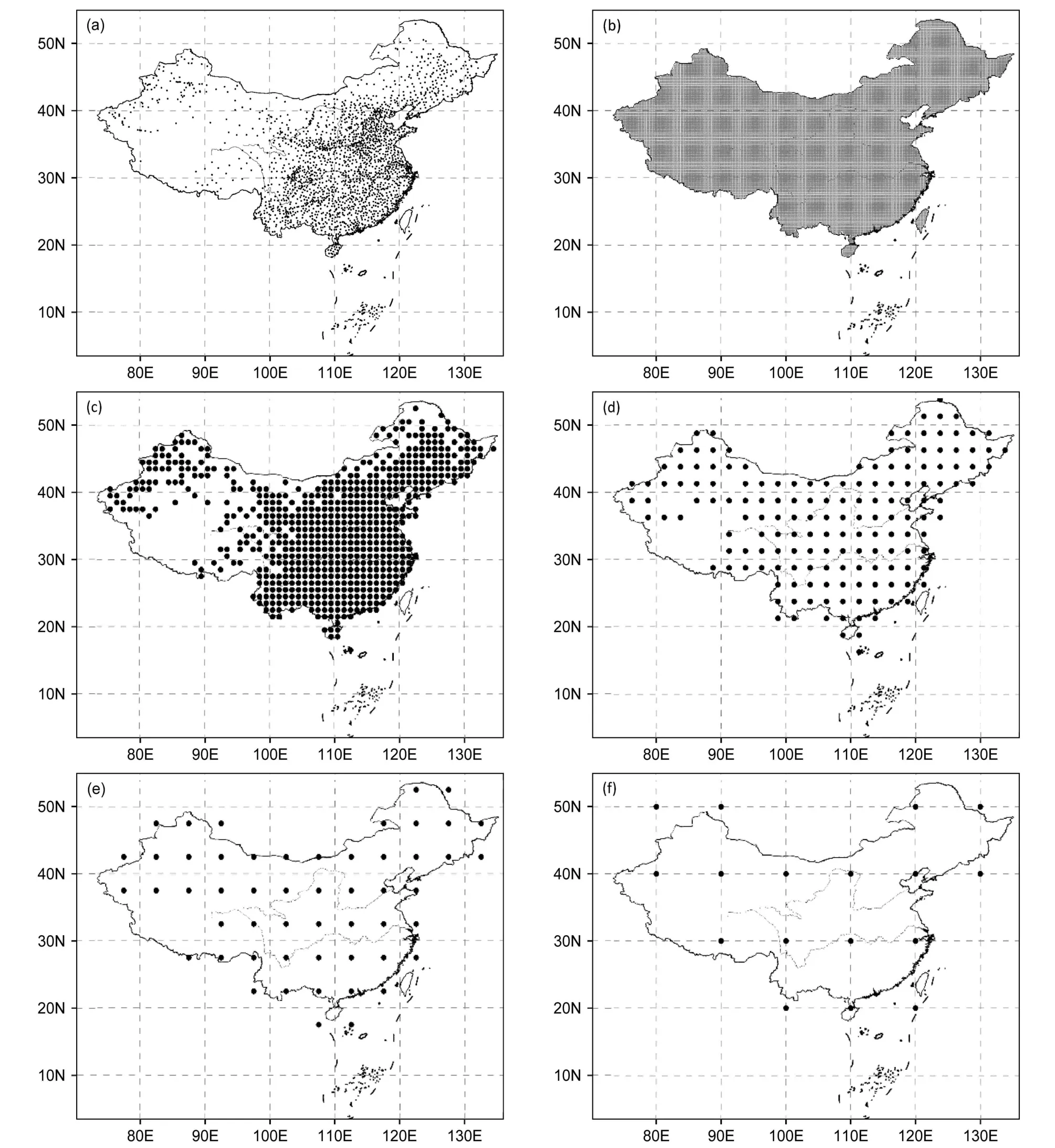
图1 中国大陆（a）地面 2377个降水观测站、（b）CMPA_Daily格点数据集格点分布；中国大陆站点数据集插值成（c）1.0°×1.0°（1°网格）、（d）2.5°×2.5°（2.5°网格）、（e）5.0°×5.0°（5.0°网格）、（f）10°×10°（10°网格）等尺度的经纬度网格空间分布Fig. 1 Spatial distribution of (a) the selected 2377 stations, (b) grids of CMPA_Daily data, (c) 1.0°× 1.0°, (d) 2.5°×2.5°, (e) 5.0°×5.0°, and (f)10°×10° grids interpolated by station data in mainland of China

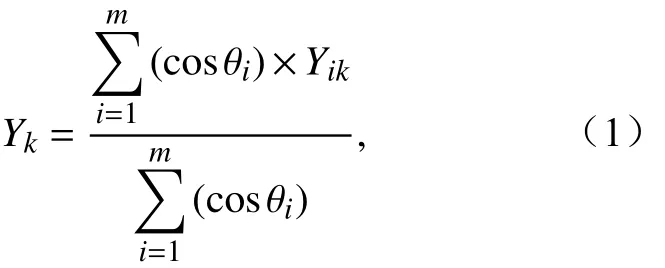
其中，Yk为第k年区域平均值,i= 1, 2, …,m（m为网格数），Yik为第i个网格中第k年的平均值，θi为第i个网格中心点的纬度。

省面积加权平均方法首先把每年每个省内所有站点的年降水量指标进行算术平均，得到各省的平均值Yik。然后将式（1）中cosθi改为各省的面积，加权计算得到全国区域平均年降水量指标时间序列。如果某年某省任何一个台站都没有数据，该省不参与计算。直接求平均方法是将范围内每年所有数据的台站的指标值直接求算平均，获得区域平均序列。参照值序列的计算方法同式（1），使用格点数据集1998～2012年的全国或者中国西部、中国东部范围内每个格点的值作为Yik，根据格点中心点的纬度余弦值cosθi加权平均。

采取上述多种区域平均方法分别计算得到1998～2012年不同降水指标序列，对比各区域平均序列与参照值序列的平均值、线性回归趋势、标准差3种指标的数值差异。其中平均值指示区域平均结果的气候学参考值有无失真，线性回归趋势可以显示出区域平均结果对降水变化的评估是否可靠，标准差反映区域平均时间序列的离散程度，表征序列是否稳定。若某种区域平均技术方法计算得到的序列的3种统计指标的数值较接近参照值，则认为该区域平均方法对台站空间分布不均匀问题的解决效果较好。

3 结果分析

不同区域平均技术方法计算所得的1998～2012年中国区域平均降水量序列平均值存在显著差异（图2、图3a、3b）。全国多年平均年降水量的参照值是652.53 mm，省面积加权平均方法所得全国多年平均降水量为627.90 mm，比参照值偏小24.63 mm，在所有区域平均方法中同参照值最为接近。2.5°网格和5.0°网格的区域平均结果分别是 718.31 mm，725.88 mm，较参照值依次偏大63.79 mm和73.35 mm。其他区域平均方法的平均值都比参照值偏大超过100 mm，均严重高估了全国平均降水量。

从1998～2012年中国区域平均年降水量的线性变化趋势来看，参照值和所有区域平均方法所得序列都为减少趋势（图2、图3a、3b）。其中，参照值的减小速率为−17.27 mm (10 a)−1。2.5°网格区域平均降水量的变化趋势为−16.88 mm (10 a)−1，比参照值偏高 0.40 mm (10 a)−1，相对最接近。其次接近的是5.0°网格区域平均降水量序列，变化趋势为−14.74 mm (10 a)−1，偏高 2.53 mm (10 a)−1。省面积加权平均降水量的线性趋势为−24.45 mm (10 a)−1，偏低 7.18 mm (10 a)−1，但仍较接近参照值。其余区域平均方法的线性回归趋势都比参照值偏小10 mm (10 a)−1以上，不宜使用（图 3c、3d）。但在降水量年际增减变化方面，2.5°网格区域平均结果比5.0°网格稍差。如参照值序列2001年降水量比2000年减少，2007年降水量比2006年增加，5.0°网格区域平均序列的增减与参照值相同，而2.5°网格序列的增减与参照值则相反（图2）。

参照值区域平均降水量序列的标准差是45.68 mm，离散程度与参照值序列最为接近的依次是2.5°网格、5.0°网格和省面积加权平均方法所得序列，标准差分别比参照值偏大0.94 mm、偏小1.93 mm、偏小3.76 mm。0.25°网格和直接平均方法的标准差比参照值均偏大15 mm以上，严重放大了区域平均降水量序列的离散程度，直接导致对全国区域平均降水量年际变率的显著高估（图2、图3e、3f）。

对不同区域平均方法的降水量距平、距平百分率、标准化距平序列的线性回归趋势与参照值进行了比较（图4）。同降水量原始值类似，所有区域平均方法所得年降水量距平序列均表现为减少趋势。参照值的线性回归趋势值为−17.30 mm (10 a)−1，基本和降水量原始值的趋势值相同。对距平值线性趋势的估计最接近参照值的也是2.5°网格和5.0°网格方法，分别为−16.80 和−14.67 mm (10 a)−1，把趋势高估了 0.50 和 2.63 mm (10 a)−1。省面积加权平均趋势比参照值偏低 7.14 mm (10 a)−1，其余区域平均方法的趋势值都比参照值偏低 10 mm (10 a)−1以上（图 4a、4b）。

引人注意的是，1998～2012年中国区域平均降水量距平百分率的参照值为增加趋势，线性回归趋势值为 7.59% (10 a)−1，与降水量原始值以及距平值的趋势相反。5.0°网格、2.5°网格、1.0°网格区域平均降水量距平百分率也是增加趋势，但增加速率明显小于参照值。分别为 2.10% (10 a)−1、2.05%(10 a)−1、0.03% (10 a)−1，对变化速率的估计偏低5%～8% (10 a)−1，但总体看对趋势的估计相对较好。其他方法的序列都有减少趋势。减少速率比参照值偏低的绝对值在8% (10 a)−1以上，省面积加权平均结果最差，比参照值偏低 11.48% (10 a)−1（图 4c、d）。

区域平均降水量参照值的标准化距平也为增加趋势，增加速率为 0.175 (10 a)−1。其他区域平均方法所得降水量标准化距平为减少趋势，变化速率与参照值相差最小的前两位是2.5°网格、5.0°网格，分别为−0.012 (10 a)−1和−0.014 (10 a)−1，比参照值偏小 0.187 (10 a)−1和 0.189 (10 a)−1，其余区域平均方法所得线性趋势比参照值偏小 0.250 (10 a)−1以上（图 4e、4f）。

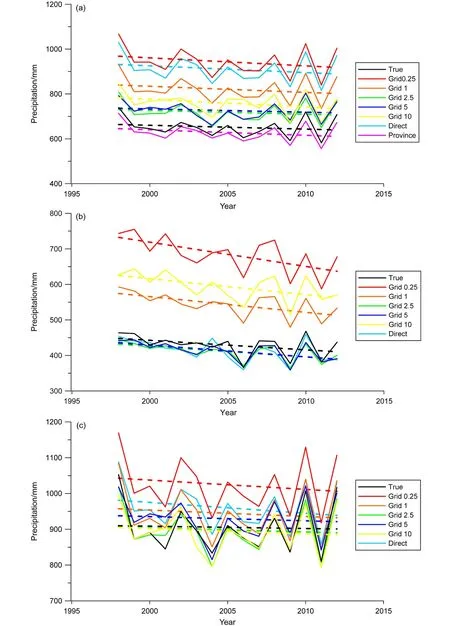
图2 不同区域平均方法所得1998～2012年（a）中国、（b）中国西部、（c）中国东部平均年降水量时间序列。True表示参照值；Grid x表示x°网格的区域平均；Province表示省面积加权平均；Direct表示算术平均Fig. 2 Time series of annual precipitation in (a) China, (b) western China, and (c) eastern China from 1998 to 2012 obtained using different regional average methods. “True” reference value; "Grid x" regional average results of the x° grids; "Province" regional average results of the provincial area weighted average method; "Direct" regional average results of the arithmetic average

无论距平、距平百分率还是标准化距平，区域平均年降水量的线性趋势和参照值最为接近的均是2.5°和5.0°网格区域平均方法所得结果。省面积加权平均距平趋势与参照值的差距绝对值较为接近，但距平百分率趋势估算的误差比其他区域平均方案都大，原因是其直接用区域平均降水量序列计算距平百分率，而相对较为合理的方法是使用各台站的年降水量分别计算台站的距平百分率，再计算省平均和区域平均。

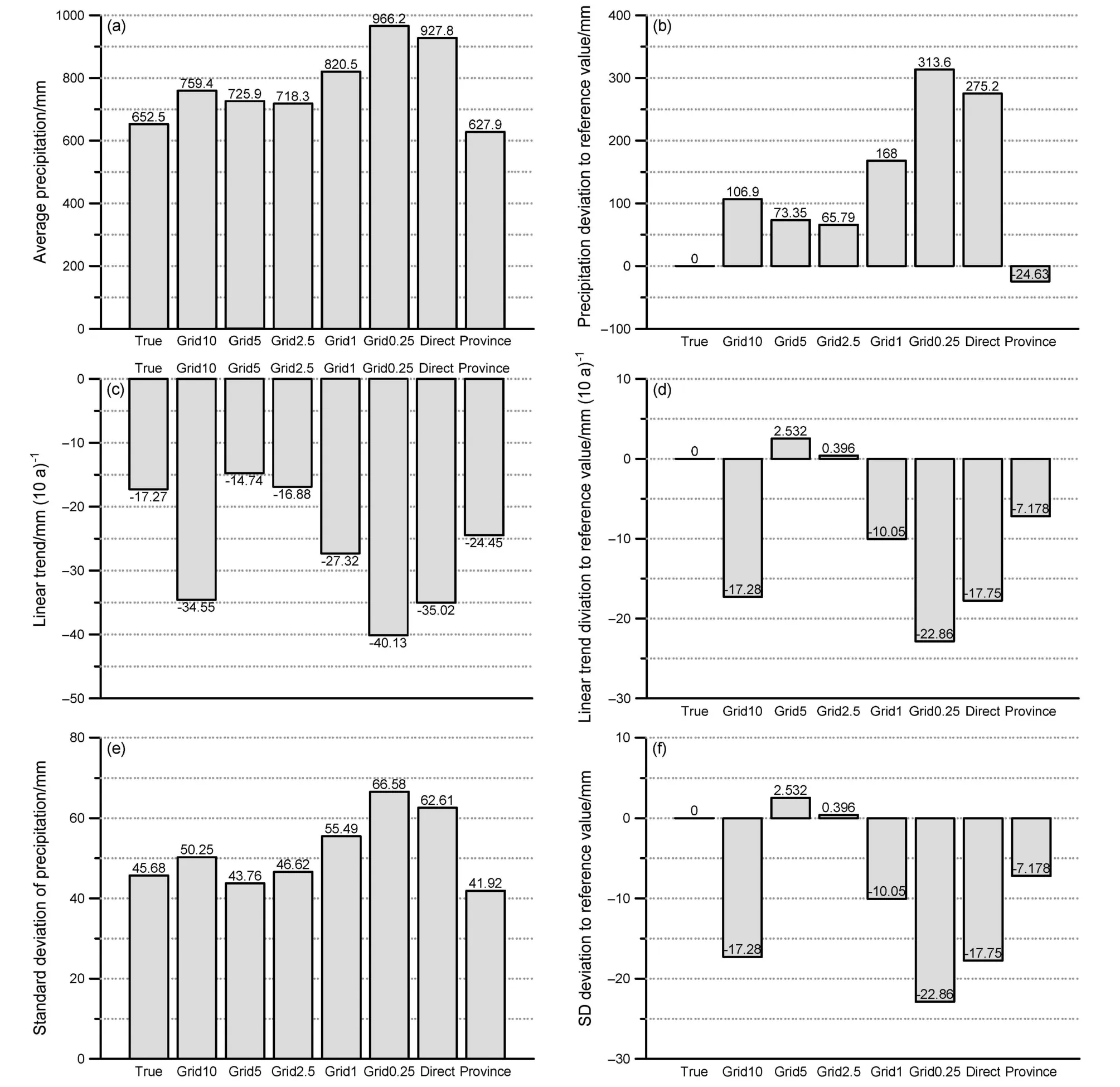
图3 不同区域平均方法所得1998～2012年中国区域平均降水量序列（a）平均值及（b）平均值和参照值的差值、（c）线性趋势及（d）线性趋势和参照值的差值、（e）标准差及（f）标准差和参照值的差值。True表示参照值；Grid x表示x°网格的区域平均；Province表示省面积加权平均；Direct表示站点直接求平均Fig. 3 Values (left column) and deviations to the reference value (right column) of annual precipitation in China averaged from 1998 to 2012 obtained using different regional average methods: (a, b) Average values; (c, d) linear trends; (e, f) standard deviations (SD). "True" reference value;"Grid x" regional average results of the x° grids; "Province" regional average results of the provincial area weighted average method; "Direct" regional average results of the arithmetic average

中国西部区域1998～2012年平均降水量参照值是429.2 mm，直接求平均所得中国西部多年平均降水量为413.1 mm，小于参照值16.2 mm，同参照值相对最接近。5.0°网格和2.5°网格区域平均结果分别是412.5 mm，410.9 mm，较参照值依次偏小16.7 mm和18.3 mm，差异也较小。其他不同尺度经纬度网格区域平均方法所得降水量多年平均值都比参照值偏大超过100 mm，会严重高估中国西部平均降水量（图5a、b）。

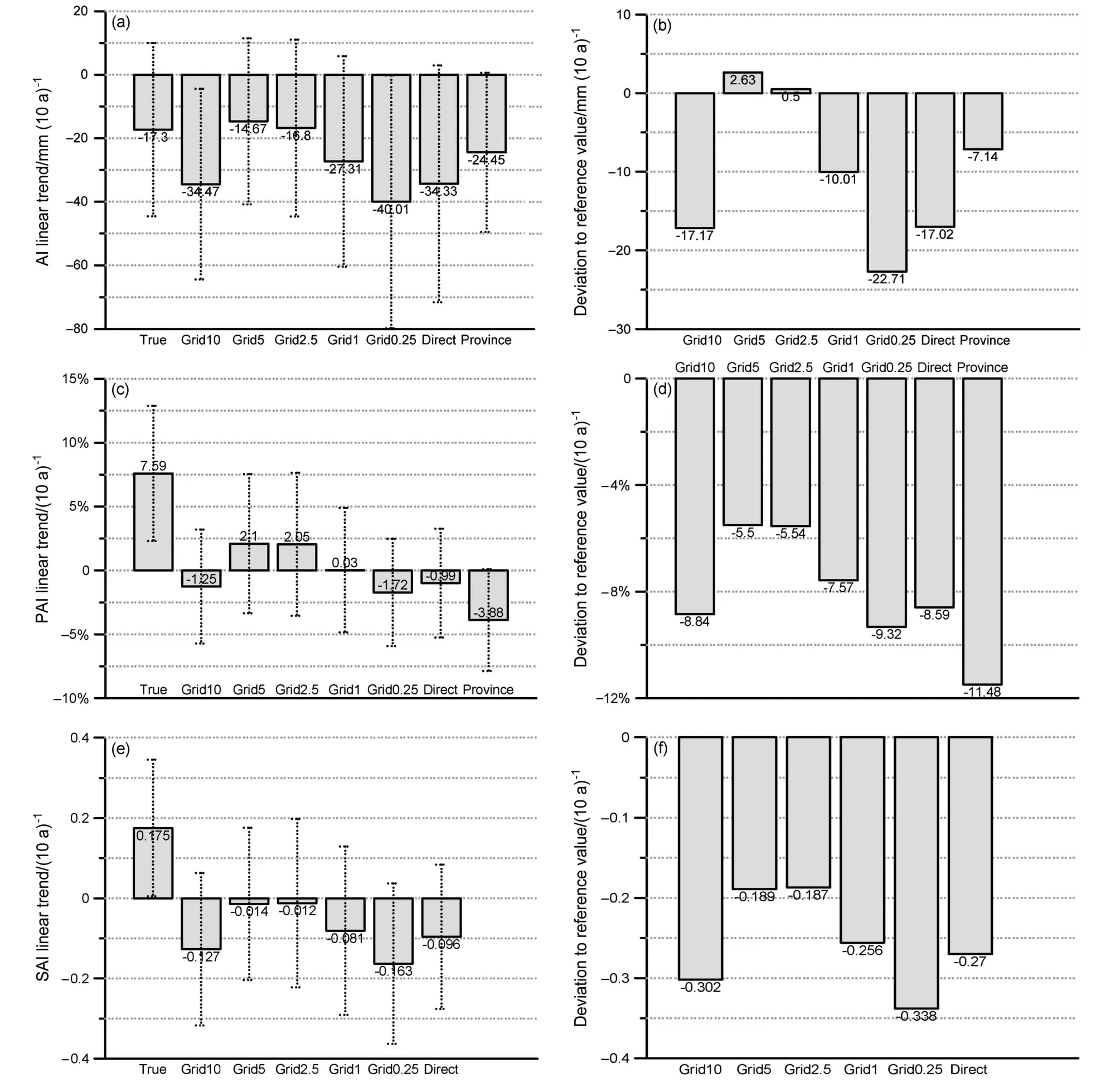
图4 不同区域平均方法所得1998～2012区域平均降水量（a）距平（AI）线性趋势及（b）距平和参照值线性趋势的差值、（c）距平百分率（PAI）线性趋势及（d）距平百分率和参照值线性趋势的差值、（e）标准化距平（SAI）线性趋势、（f）标准化距平和参照值线性趋势的差值。True表示参照值，Grid x表示x°网格的区域平均，Province表示省面积加权平均，Direct表示算术平均；（a、c、e）中误差线为线性回归斜率的1个标准差不确定范围Fig. 4 Values (left column, the error line is the uncertainty range of one standard deviation of the slope of linear regression) and deviations to the reference value (right column) of linear trends for (a, b) anomaly (AI), (c, d) percentage of anomaly (PAI), and (e, f) normalized anomaly (SAI) of annual precipitation in China from 1998 to 2012 obtained using different regional average methods. "True" reference value; "Grid x" regional average results of the x° grids; "Province" regional average results of the provincial area weighted average method; "Direct" regional average results of the arithmetic average. The error lines in (a, c, e) are ranges of one standard deviation

1998～2012年中国西部区域平均年降水量参照值和所有区域平均方法的计算结果都表明，中国西部区域平均降水量存在减少趋势（图2、图5）。参照值的变化速率为−26.91mm (10 a)−1，其他所有的区域平均方法所得序列的减小速率都更显著。其中，2.5°网格区域平均变化速率为−29.80 mm (10 a)−1，比参照值偏低 2.89 mm (10 a)−1，相对最接近参照值。其次接近的是 5.0 度网格，变化趋势为−33.09 mm(10 a)−1，偏低 6.18 mm (10 a)−1。台站直接平均降水量的线性趋势为−34.27 mm (10 a)−1，偏低 7.35 mm (10 a)−1。其余区域平均方法的线性回归趋势都比参照值小15 mm (10 a)−1以上（图 5c、5d）。

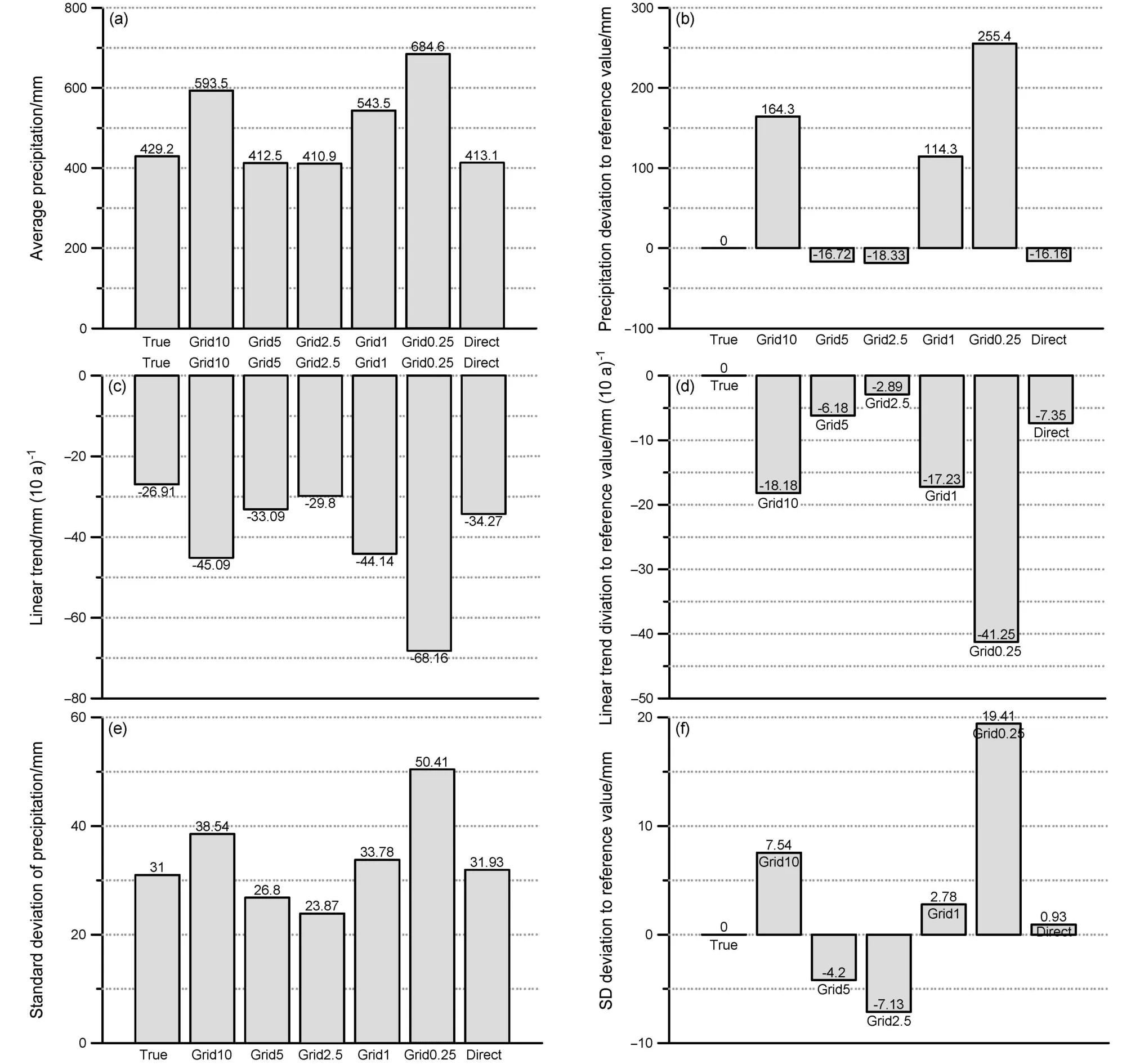
图5 不同区域平均方法所得1998～2012年中国西部区域平均降水量序列（a）平均值及（b）平均值和参照值的差值、（c）线性趋势及（d）线性趋势和参照值的差值、（e）标准差及（f）标准差和参照值的差值。True表示参照值；Grid x表示x°网格的区域平均；Province表示省面积加权平均；Direct表示站点直接求平均Fig. 5 Values (left column) and deviations to the reference value (right column) of annual precipitation in western China from 1998 to 2012 obtained using different regional average methods: (a, b) Average values; (c, d) linear trends; (e, f) standard deviations. "True" reference value; "Grid x" regional average results of the x° grids; "Province" regional average results of the provincial area weighted average method; "Direct" regional average results of the arithmetic average

西部区域平均降水量参照值序列的标准差是31.00 mm，离散程度较为接近参照值序列的依次是直接平均、1.0°网格、5.0°网格、2.5°网格、10°网格和0.25°网格区域平均方法。0.25°网格平均方法的标准差最大，比参照值均偏大19.41 mm，会严重放大区域平均降水量的离散程度，导致了对区域平均降水量减少速率的高估；反之，2.5°网格区域平均降水量序列的离散程度最小，低估了区域平均降水量序列的波动振幅（图2、图5e、f）。

1998～2012年，中国东部区域平均多年平均年降水量的参照值是905.3 mm，2.5度网格区域平均方法所得中国东部多年平均降水量为898.2 mm，小于参照值7.13 mm，同参照值最为接近。10°网格和5.0°网格的区域平均结果分别是894.8 mm，929.6 mm，依次较参照值偏小 10.5 mm和偏高24.3 mm。其他大小的经纬度网格区域平均方法和直接平均方法所得中国东部平均降水量都比参照值明显偏大（图6a、b）。

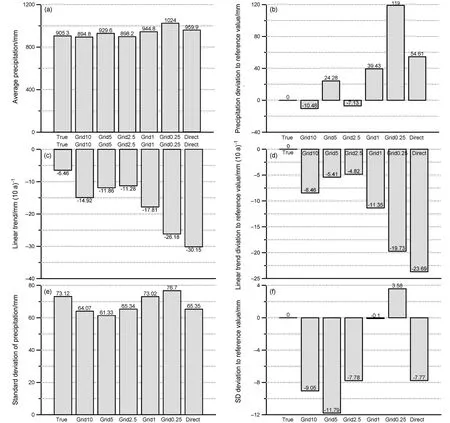
图6 不同区域平均方法所得1998～2012年中国东部区域平均降水量序列（a）平均值及（b）平均值和参照值的差值、（c）线性趋势及（d）线性趋势和参照值的差值、（e）标准差及（f）标准差和参照值的差值。True表示参照值；Grid x表示x°网格的区域平均；Province表示省面积加权平均；Direct表示站点直接求平均Fig. 6 Values (left column) and deviations to the reference value (right column) of annual precipitation in eastern China from 1998 to 2012 obtained using different regional average methods: (a, b) Average values; (c, d) linear trends; (e, f) standard deviations. "True" reference value; "Grid x" regional average results of the x° grids; "Province" regional average results of the provincial area weighted average method; "Direct" regional average results of the arithmetic average

中国东部平均降水量参照值序列和所有区域平均方法所得序列都表明，1998～2012年降水量有所减少。其中参照值序列的线性回归趋势为−6.46 mm (10 a)−1，其他所有的区域平均方法所得序列的线性趋势值都比参照值偏低。其中，2.5度网格区域平均年降水量变化速率为−11.12 mm (10 a)−1，比参照值的趋势偏低 4.67 mm (10 a)−1，同参照值相对最为接近。5.0度网格区域平均序列的变化趋势为−11.61 mm (10 a)−1，偏低 5.15 mm (10 a)−1，效果也较好。10度网格区域平均降水量的线性趋势值为−14.59 mm (10 a)−1，偏低 8.23 mm (10 a)−1。其余区域平均方法的线性回归趋势都比参照值小10 mm(10 a)−1以上，其中直接平均方法所得趋势与参照值差异最大，差值达到 23.69 mm (10 a)−1（图 6c、6d）。

东部区域平均降水量参照值序列的标准差为73.12 mm，序列离散程度与参照值最为接近的是1.0°网格，与参照值的离散程度相差无几。10°网格、5.0°网格、2.5°网格和直接平均等方案所得区域平均序列的离散程度都比参照值明显偏小，其中5.0°网格区域平均序列的标准差最小，和参照值差异最大，会明显减弱区域平均序列的波动。只有0.25°网格区域平均方法所得序列的离散程度大于参照值，标准差偏大 3.58 mm（图 6e、6f）。

中国西部、中国东部不同区域平均方法所得降水量距平、距平百分率、标准化距平序列的线性回归趋势和参照值的比较结果与年降水量的结果较为类似。总之，在中国西部以及中国东部，对区域平均降水序列估计效果最好的方案均为2.5°网格区域平均方法。5.0°区域平均方案次之。直接求平均的方案在台站数量较少的中国西部地区应用时，效果似好于全国区域，但仍不适用于台站数量多的中国东部。

4 讨论

本文研究发现，在台站资料准确性好，基本无缺测的1998～2012年，中国大陆全部、中国西部以及中国东部的最优区域平均方法都是2.5°网格区域平均方法，该网格尺度也和国际主流格点降水产品 CMAP（CPC Merged Analysis of Precipitation）、GPCC（Global Precipitation Climatology Centre）等的网格尺度吻合，可以在最大程度上解决当前观测台站空间分布不均匀引起的估计误差问题。

不同方法所得区域平均序列之间的差异来源于地面观测台站的空间分布。为确定本文所得结论是否具有普适性，对差异原因进行了分析和讨论。中国西部和东部地区的平均降水量背景场差异巨大，如果某区域平均方法参与计算的东西部网格比值和实际东西部面积之比差异很大，全国区域平均结果显然不可靠。表2比较了不同网格尺度下，中国东部网格和西部网格的数量之比，CMPA_Daily格点数据集的东西部网格数目之比是1.475，基本等同于真实的中国东西部面积之比（表2）。站点数据插值成的网格越小，该比值越大，只有10度网格的网格数量比值小于实际，其余尺度网格数量比值均大于实际。1.0°网格在中国西部地区的空网格多于2/3，东部地区也有少量空网格存在（图1）；绝大部分的0.25°网格内都只有一个台站，网格数目与站点数目相差无几，东西部网格与台站的数量比值均超过10，应当是0.25°网格以及直接站点平均两种方法所得序列准确性较差的主要原因。省面积加权平均方法的省平均值相当于直接求算术平均，在台站空间分布差异大的西藏、青海、新疆、内蒙古、黑龙江等省区内，也相当于出现了较多空网格。

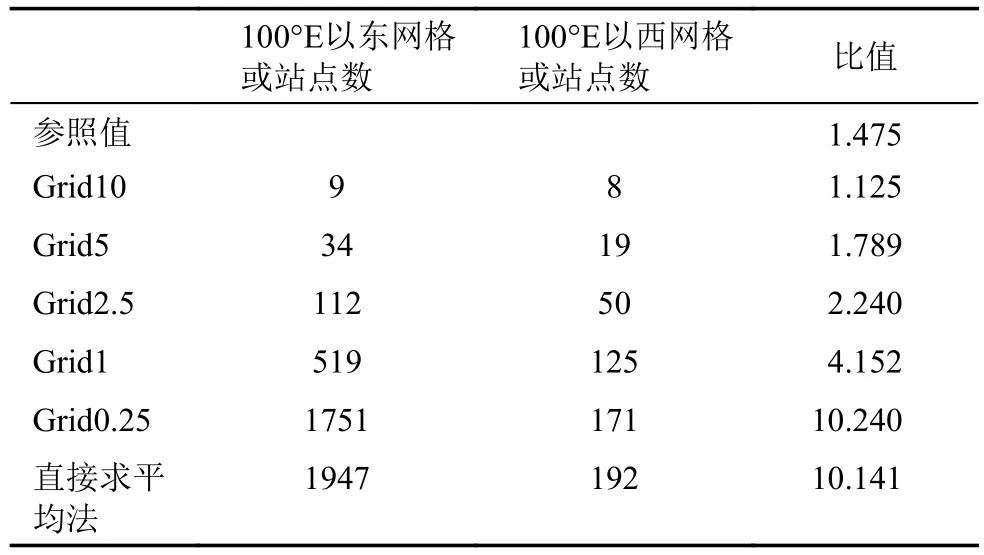
表2 不同尺度的经纬度网格加权平均计算方法（Grid x），直接求平均法中参与计算的中国东部与西部网格或观测台站数量之比Table 2 Ratios of the eastern grids/stations to the western grids/stations at different grid scales (Grid x) or reference values

降水观测站点的东西分布并不是区域平均方法优劣的唯一因素。虽然中国东西部2.5°网格数量的比值与实际的偏差大于5.0°网格和10°网格，但由于10°和5.0°网格的边缘网格面积估算误差较大，对公式（1）Yik权重的估计精度较差，导致区域平均结果劣于2.5°网格。较小的网格边缘面积的误差小，省面积平均方法没有面积误差，但由于两者存在空网格多的问题，其区域平均序列同样存在显著偏差。两者权衡，无论台站稀疏的中国西部还是台站密集度很高的中国东部，本文选用的方法中效果最好的都是2.5°网格和5.0°网格，二者较好的平衡了面积误差和空网格误差两种主要误差来源。鉴于当前中国乃至全球大多数地区的地面观测站空间密度不会偏离这两种情况太多，在计算区域平均降水量序列时选择2°～5°之间的经纬度网格进行面积加权平均的方案都是最合适的。空间范围较小、台站较密集时，应当使用2.5°左右网格的区域平均方案；反之空间范围较大、台站较稀疏，导致空网格出现率多，应选择5.0°左右的网格平均方案。

本文研究结论的一个重要前提，是多源融合降水数据集CMPA_Daily作为参照值，其区域平均序列可准确反映实际的面雨量。尽管先前的诸多研究指出CMPA_Daily产品对降水量的估计效果好，但其准确性是以自动站仪器观测资料为真值进行检验的（宇婧婧等, 2015）。在自动站资料空间密度低的中国西部许多区域（如青藏高原地区），卫星产品在融合降水量中的权重较大，缺少检验。因此，在这些地区基于CMPA_Daily产品估计的降水量准确性尚需进一步确认。此外，由于多源融合降水产品的时间序列较短，本文只分析得到了站点资料完整性和准确性很好的1998～2012年的最优区域平均方法。在气候监测业务和科研工作中常用的几十年尺度的站点资料中存在一定数量的疑误和缺测数据，最优区域平均方案是否对其敏感，也需要进一步分析确认。

5 结论

本文以中国地区的地面与CMORPH融合逐日降水产品的区域平均年降水量序列作为参照值，比较多种区域平均方法所得1998～2012年降水量序列与参照值的差异，分析得到了以下主要结论：

（1）在数据完整性和准确性好的 1998～2012年，2.5°网格和5.0°网格面积加权区域平均方法所得序列与参照值最为接近，对中国以及东西部平均降水的估计效果好，分别是最优和次优的区域平均方法，适用于大尺度的区域平均降水量序列构建以及气候变化分析工作。直接求平均以及很小网格面积加权区域平均方法所得序列则与参照值差异较大，可靠性较低。

（2）1998～2012年，全国区域平均降水量原始值以及距平的参照值都有减少趋势，但降水量距平百分率和标准化距平表现为增加趋势。各种区域平均方法都对距平百分率和标准化距平的变化趋势存在一定程度上的低估，其中2.5°和5.0°网格区域平均方法对序列趋势值的低估程度最小。

（3）气候业务中常用的“省面积加权平均方法”对全国年降水量多年平均值的计算最准确，但其对趋势的估计效果不如2.5°和5.0°网格。此外，其对年降水量距平百分率的计算方法有一定问题，存在改进空间。

本文研究是以多源融合降水数据集CMPA_Daily作为参照值，评价各种区域平均序列的可靠性；但多源融合降水数据在中国西部区域仍缺少充分检验，同时这套降水数据产品的时间序列也较短，因此本文分析评价结果仍需进一步研究确认。