不同大气强迫作用下陆面模式CAS-LSM多年冻土活动层厚度模拟与不确定性研究

李锐超 谢瑾博 谢正辉

1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京 100029

2 中国科学院大学地球与行星科学学院，北京 100049

1 引言

冻土在北半球分布广泛，约占其陆地面积的25%（Muller et al., 1947; Zhang et al., 1999）。由于气候变暖，近年来多年冻土退化严重、反映地壳表层每年寒季冻结、暖季融化岩土层的活动层厚度不断增加（Delisle, 2007; Koven et al., 2013）。近 20年来青藏高原多年冻土相对面积减少4.3%，约3.1×104km2，相应的季节冻土面积增加 3.1×104km2（ 张 国 胜 等 , 2007; Yang et al., 2010; 徐 晓 明 等 ,2017）。多年冻土活动层厚度受气候条件的驱动，并与海拔、经纬度、活动层岩性、含水特征、地面温度以及下垫面性质有关。另一方面，冻土活动层厚度变化影响陆气之间的水分能量交换以及生态系统的碳循环过程，对天气以及气候过程产生重要影响。随着活动层厚度的增加，北极多年冻土中储存着大量的二氧化碳、甲烷等温室气体会释放到大气中，进一步加剧全球变暖（Schuur et al., 2015）。世界气候研究计划WCRP已经将活动层厚度的变化研究列为气候和冰冻圈CLIC计划的主要观测研究内容之一（Brown et al., 2000; Nelson et al., 2004）。这些都表明研究多年冻土区活动层厚度变化及其影响的重要性。

早期开展的环北极多年冻土区活动层厚度以及近地表冻土变化的监测表明：在过去几十年里，北极地区的活动层厚度不断增加，其中俄罗斯北极地区活动层厚度增加较多，增加了约22 cm（Harris et al., 2003; Frauenfeld et al., 2004）。近几十年来青藏高原多年冻土活动层厚度也表现出明显增加的趋势，对水文过程、生态系统碳循环过程、气候变化、寒区工程以及基础设施等影响巨大（Zhao et al.,2004; 李元寿等, 2010; Wu and Zhang, 2010; 张中琼和吴青柏, 2012）。多年冻土区主要分布在北半球高纬度以及高山地区。在大尺度空间和时间上活动层厚度观测数据稀少，利用陆面过程模式结合各种观测进行模拟是研究多年冻土活动层厚度在大尺度空间和时间上变化的重要工具。通过对冻土参数化方案的改进，陆面过程模式对冻土的模拟已经取得了很大进展（Lawrence et al., 2008, 2012; Xie et al.,2018; Gao et al., 2019）。Guo et al.（2017）利用陆面过程模式 CLM4.5（Lawrence et al., 2012）模拟的土壤温度插值得到活动层厚度，由此研究了多年冻土分布以及活动层厚度的变化趋势。Gao et al.（2019）将双向Stefan算法耦合到通用陆面过程模式CLM4.5中，发展考虑土壤冻结融化界面动态变化的陆面过程模式CAS-LSM。该模式不仅能够模拟土壤冻结融化界面的动态变化，同时也可以模拟活动层厚度。在陆面模式中引入了求解活动层厚度的新方法。该方法有利于推进陆面模式中多年冻土活动层模拟研究，并为活动层模拟提供额外新的有用信息。另一方面，多年冻土以及活动层厚度的模拟也受到大气强迫数据集的影响（Guo et al.,2012; Lawrence et al., 2012）。Guo et al.（2012）采用动力降尺度对大气强迫数据进行了校正减小青藏高原多年冻土模拟的偏差。Lawrence et al.（2012）通过改进大气强迫数据中的气温和降水估计，模拟的多年冻土退化速率降低了29%。

本研究我们采用陆面过程模式CAS-LSM，利用陆面模式比较计划 LS3MIP（Van den Hurk et al.,2016） 中 4 套 强 迫 数 据 GSWP3（ Kim, 2017）、WFDEI（ Haddeland et al., 2011; Weedon at al.,2014）、 CRU-NCEP（ Viovy and Ciais, 2009）、Princeton（Sheffield et al., 2006），驱动 CAS-LSM进行模拟试验，通过对活动层厚度及其变化趋势在不同强迫下的模拟与分析，研究不同大气强迫作用下陆面过程模式CAS-LSM对于活动层厚度的模拟与不确定性。

2 数据和方法

2.1 数据

本研究采用的大气强迫数据是陆面模式比较计划LS3MIP中的4组强迫数据，分别是CRU-NCEP（Climatic Research Unit-NCEP forcing data）（Viovy and Ciais, 2009）、 GSWP3（ Global Soil Wetness Project forcing dataset）（ Kim, 2017）、 Princeton（Princeton meteorological forcing dataset）（Sheffield et al., 2006）、 WFDEI（ water and global change forcing data methodology applied to ERA-Interim data）（Haddeland et al., 2011; Weedon at al., 2014）。强迫数据包括气温、风速、湿度、太阳辐射和降水。CRU-NCEP是两套数据的组合：气候研究中心CRU TS v3.2的气候数据和美国国家环境预报中心NCEP的再分析数据。其中降水、温度、太阳辐射、相对湿度是基于CRU的数据，长波辐射、气压、风速是由NCEP数据插值得到的，空间分辨率0.5°（纬度）×0.5°（经度），时间分辨率 6 h，时间周期1901～2010年。GSWP3是基于20世纪的再分析数据动力降尺度而来的，利用CRU TS v3.21、全球降水气候中心GPCC v7和地表辐射收支数据集分别对温度、降水、长波辐射和短波辐射进行偏差校正。空间分辨率0.5°（纬度）×0.5°（经度），时间分辨率 3 h，时间周期 1901～2014年。Princeton是由 NCEP的再分析数据与CRU的数据以及基于卫星的降水数据结合而来，其中降水数据是基于全球降水气候项目（GPCP）和热带降雨测量项目（TRMM）统计降尺度而来。空间分辨率0.5°（纬度）×0.5°（经度），时间分辨率 3 h，时间周期 1901～2012 年。WFDEI 包含两部分数据，WFD（WATCH force Data）（1901～1957年）基于欧洲中期天气预报中心重新整理的ERA-40 数据得到的，WFD（WATCH force Data）（1958～2001年）基于欧洲中期天气预报中ECMWFERA-40再分析数据得到的，其中温度和降水均来自ERA-40，并且利用全球降水气候项目（GPCP）和气候研究中心（CRU）数据进行偏差校正，空间分辨率0.5°（纬度）×0.5°（经度），时间分辨率3 h，时间周期1901～2001年。WFDEI是基于ECMWFERA-Interim再分析数据得到的，其中温度和降水均来自ERA-Interim，并且利用全球降水气候项目（GPCP）和气候研究中心（CRU）数据进行偏差校正，空间分辨率0.5°（纬度）×0.5°（经度），时间分辨率3 h，时间周期1979～2014年。这些强迫数据已被应用与陆面模式比较LS3MIP（Van den Hurk et al., 2016）。

活动层厚度的观测数据来自北极活动层观测网（CALM）（Brown et al., 2000）（http://www.gwu.edu/～CALM/[2019-09-05])站点观测数据。CALM的观测数据时间周期是1990～2010年。本研究选取了1996～2010年期间CALM的50个观测站的活动层厚度数据，因为大多数观测站在这段期间是有连续的记录。这些站点主要集中在俄罗斯地区以及阿拉斯加地区。

2.2 陆面过程模型CAS-LSM的冻融过程方案

CAS-LSM是以美国国家大气科学中心所发展的陆面过程模式 CLM4.5 为基础（Oleson et al.,2013）, 耦合了自主发展的考虑地下水侧向流（Zeng et al., 2016a, 2016b）、人类取用水活动（Zou et al.,2014, 2015; Zeng et al., 2017）、 冻 结 融 化 界 面（Gao et al., 2016, 2019）以 及 河流 氮 输送 过 程（Liu et al., 2019）的方案，该模式已应用于中国黑河流域研究（Xie et al., 2018）。模式较好地再现了地下水、蒸发蒸腾和冻土的分布，与地表温度、热通量时间变化吻合较好。本研究的工作主要涉及土壤冻结融化界面的动态变化这一模块，该模块描述如下：

冻结融化界面的计算方法（Jumikis, 1978; Gao et al., 2016, 2019）：

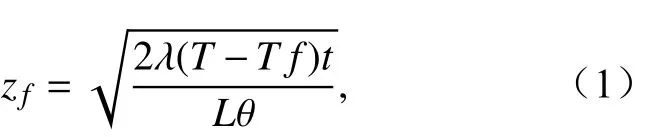
对公式（1）两边取平方得：

对公式（2）中的D求微分得：

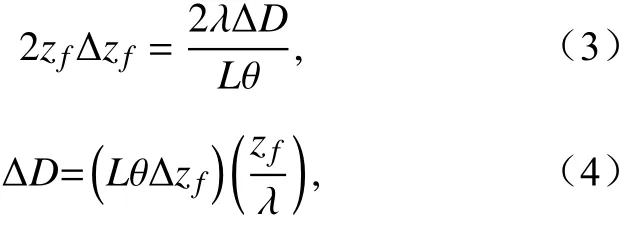
其中，在陆面模式中土壤垂直分为15层，我们定义i为土壤层数，为 第i层土壤的深度，为第i层土壤的厚度，为第i层土壤的热传导率，为第i层土壤的热传输阻力为冻融界面通过第i层土壤所需的冻融指数，首先计算冻融界面通过第一层土壤所需的冻融指数，即，此过程中从0增长至，将平均分成层，可近似表示为

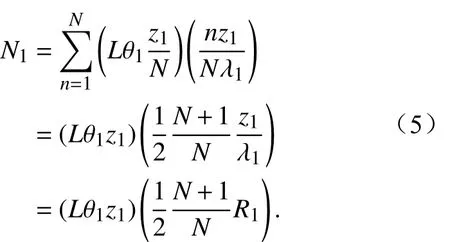
同理可得，

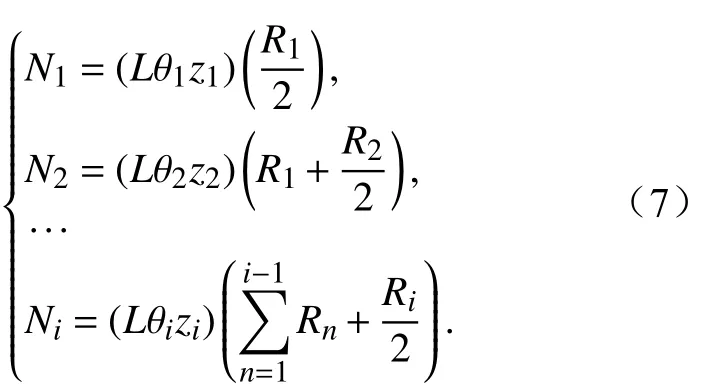
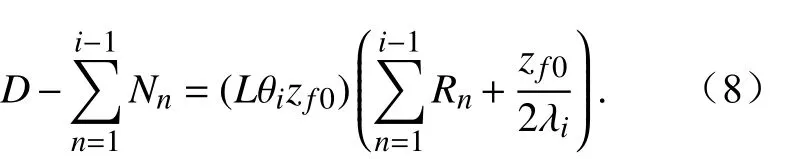
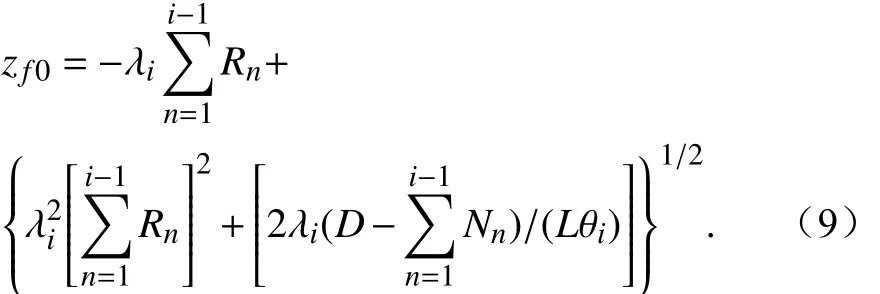
那么从地表算起的冻结或融化深度可表示为

该算法与陆面过程模式CAS-LSM是实时耦合。计算时需要输入地表温度以及各层土壤的相关性质，同时将得到土壤冻结融化界面信息加入到原有土壤分层中。原土壤分层信息不变，增加土壤冻结融化界面这一层。新增加这一层土壤是按照陆面模式的分层方式（Oleson et al., 2013）加入的。计算新土壤分层的土壤温度，之后将新土壤分层的温度返回原土壤分层。从而更加合理地模拟高寒区域冻融状况，具体过程可参见（Oleson et al., 2013; Gao et al.,2016, 2019）。CAS-LSM不仅能够模拟土壤冻结融化界面的动态变化，同时也可以模拟活动层厚度。该方法有利于推进陆面模式中多年冻土活动层模拟研究，并为活动层模拟提供额外新的有用信息。

2.3 试验设计

本研究采用陆面过程模式CAS-LSM进行4组数值试验，分别采用4组不同的大气强迫数据（GSWP3、WFDEI、CRU-NCEP、Princeton）驱动CAS-LSM，进行全球模拟，陆面模式的模拟时间积分步长为1800 s，模拟开始时首先将大气强迫数据插值到陆面模式的模拟时间积分步长上，然后进行模拟，模拟时间为1901～2010，空间分辨率为0.9°（纬度）×1.25°（经度）。为使模式达到平衡，利用CRU-NCEP 20年（1901～1920年）的大气强迫数据循环强迫，结果作为4组数值模拟试验的初始场。最后对1901～2010进行正式模拟（月输出结果），结果分析时段为1960～2009年。4组试验除了大气强迫数据不同外，其余设置（如模拟区域、步长、初始场等）均相同。

2.4 分析方法

在陆面模式中多年冻土的定义：在模式土壤分层的前10层（相当于3.8 m）土壤中，至少有1层的土壤温度连续24个月低于0℃（Lawrence et al.,2012）。应该指出的是这里多年冻土的定义代表的是“近地表多年冻土”。一般来说，近地表多年冻土比深层多年冻土对气候变化更敏感（Lawrence et al., 2008）。

活动层厚度的定义是多年冻土在一年中最大融化深度（Lawrence et al., 2012）。本研究中的活动层厚度是通过CAS-LSM计算得到。CAS-LSM通过耦合Stefan算法来模拟活动层厚度。一般来说，在陆面模式中活动层厚度可以通过土壤温度插值计算得到（Lawrence et al., 2012; Guo et al., 2017）。因此我们也给出了通过土壤温度插值计算得到活动层厚度，并且将两种方法所得到活动层厚度与观测值进行了比较。为了说明CAS-LSM模拟的活动层厚度是合理的。对于气候态的活动层厚度验证，我们将每个站点都有记录的观测数据进行气候态平均，然后与站点相对应的网格数据平均值进行比较验证。使用平均偏差、均方根误差和相关系数来评价模拟结果与观测结果的一致性。采用最小二乘拟合法计算趋势作为线性回归的斜率，采用Mann- Kendall检验评价线性趋势的统计意义。

图1 1996～2010 年（a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的活动层厚度（蓝点）、土壤温度插值的活动层厚度（红点）与CALM观测数据验证Fig. 1 Simulated active layer thickness validation (blue point) using four atmosphere forcing data (a) CRU-NCEP (Climatic Research Unit-NCEP forcing data), (b) GSWP3 (Global Soil Wetness Project forcing dataset), (c) Princeton (Princeton meteorological forcing dataset), and (d) WFDEI(water and global change forcing data methodology applied to ERA-Interim data) and the soil temperatures interpolationed active layer thickness validation (red point) based on observations from CALM (Circumpolar Active Layer Monitoring) sites during 1996–2010

3 模拟多年冻土区活动层厚度的变化

3.1 站点验证

首先将不同强迫下模拟所得到的活动层厚度数据与观测数据进行验证，图1给出了4种强迫下（CRU-NCEP、GSWP3、Princeton、WFDEI）模拟的1996～2010年平均活动层厚度与CALM观测数据验证的散点图。蓝色的点为CAS-LSM模拟得到的活动层厚度，红色的点为土壤温度插值得到的活动层厚度数据。由图1可知不同强迫下CASLSM模拟得到的活动层厚度和观测值比较接近，土壤温度插值得到的活动层厚度和观测值也比较接近。同时与观测相比都表现出偏大的趋势。活动层厚度观测数据的平均值为0.86 m，CAS-LSM模拟得到的活动层厚度分别为 1.47 m、1.28 m、1.48 m、1.26 m。土壤温度插值得到的活动层厚度分别为1.28 m、1.19 m、1.4 m、1.18 m。CAS-LSM 模拟得到的活动层厚度与观测的平均偏差分别为0.61 m、0.42 m、0.62 m、0.40 m，均方根误差分别为 1.04 m、0.85 m、0.92 m、0.78 m，相关系数分别为 0.44、0.53、0.61、0.64。土壤温度插值得到的活动层厚度与观测值的平均偏差分别为0.42 m、0.33 m、0.54 m、0.32 m，均方根误差分别为0.85 m、0.86 m、0.81 m、0.79 m，相关系数分别为 0.47、0.43、0.62、0.55。从平均偏差、均方根误差与相关系数上可以看出，这两种该方法模拟得到的活动层厚度差别不大，从而表明CAL-LSM模拟的活动层厚度合理。从平均偏差、均方根误差与相关系数上可以看出，强迫数据WFDEI模拟的活动层厚度与观测数据最为接近，整体结果优于其他3种强迫数据的模拟。

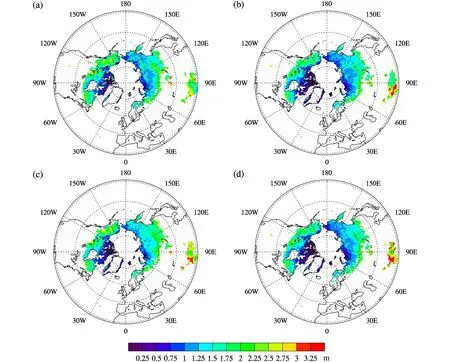
图2 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年活动层厚度的空间分布Fig. 2 Simulated mean active layer thickness using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c) Princeton, and (d) WFDEI during 1960–2009

3.2 多年冻土活动层厚度空间分布及变化趋势

我们主要分析多年冻土活动层厚度50年（1960～2009年）平均的空间分布及变化趋势。从图2可以看出，4组试验模拟的活动层厚度在气候态（1960～2009年）平均上表现出空间相似性。除青藏高原外，模拟的活动层厚度随纬度的增加而减小，活动层厚度在靠近多年冻土与季节性冻土分界线的区域深度较深。表1中区域平均的活动层厚可以看出CRU-NCEP和Princeton模拟的活动层厚度较深，WFDEI和GSWP3模拟的活动层厚度较浅。图3中活动层厚度的变化趋势基本为正值，表现逐年增加的趋势，区域平均的变化趋势分别为0.3 cm/a、0.295 cm/a、0.27 cm/a 和 0.5 cm/a，4 组模拟的平均趋势为0.34 cm/a。青藏高原地区（28°N～38°N，73°E～104°E）、北美地区（56°N～70°N，70°W～165°W）、欧亚大陆北部地区（54°N～72°N，72°E～178°E）的区域平均活动层厚度以及变化趋势见表1。4组模拟在这3个地区的区域平均厚度及变化趋势分别为2.53 m、1.16 m、1.38 m 和0.56 cm/a、0.35 cm/a、0.37 cm/a。图 4 模拟的是青藏高原地区 （ 28°N～ 38°N， 3°E～ 104°E）、 北 美 地 区（56°N～70°N，70°W～165°W）、欧亚大陆北部地区（54°N～72°N，72°E～178°E）1960～2009 年活动层厚度年际变化。从图4中可以看出，1960～2009年活动层厚度总体上表现出增加的趋势。

表1 1960～2009年利用4组大气强迫数据模拟的活动层厚度区域平均值及其变化趋势Table 1 Simulated regional average active layer thickness and its trends from 1960 to 2009 using four atmosphere forcing data

图3 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年活动层厚度变化趋势Fig. 3 Simulated active layer thickness trends (cm/a) using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c) Princeton, and (d) WFDEI during 1960–2009

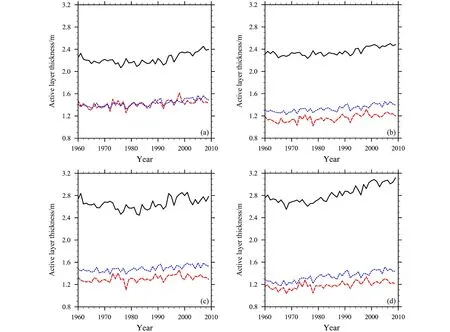
图4 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年区域平均活动层厚度年时间序列。黑线：青藏高原地区（28°N～38°N，73°E～104°E），红线：北美地区（56°N～70°N，70°W～165°W），蓝线：欧亚大陆北部地区（54°N～72°N，72°E～178°E）Fig. 4 Simulated active layer thickness annual time series using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c) Princeton, and (d)WFDEI during 1960–2009. Black line: Qinghai–Tibet plateau region (28°N–38°N, 73°E–104°E), red line: North America (56°N–70°N, 70°E–165°E),blue line: north of Eurasia (54°N–72°N, 72°E–178°E)

对于不同强迫造成的活动层厚度模拟差异，我们主要从强迫数据本身分析。首先我们采用Stefan方法模拟活动层厚度，由于地表温度是形成多年冻土的关键因素，Stefan利用地表温度来计算单层土柱冻融深度，是一种半经验方法。不同强迫模拟地表温度的不同会造成活动层厚度模拟的差异，从图5中我们可以看出，地表温度变化趋势基本为正值，也就是说地表温度整体呈现出增加的趋势，变化趋势分别为 0.036℃/a、0.036℃/a、0.035℃/a和0.061℃/a，4组模拟的平均趋势为0.042℃/a。由于地表温度增加，进而会导致活动层厚度的增加，地表温度的增加趋势是与活动层厚度的增加是一致的。图3和图5中青藏高原的部分区域出现了活动层厚度变薄、地表温度降低的趋势。然而强迫数据中的2 m气温所在的这些区域都是增加的。这可能由于陆面模式在该地区的地表参数、物理参数化方案等造成的，具体还需要针对这一地区结合观测数据进行深入研究。总体来看，除青藏高原的部分区域外，2 m气温以及地表温度的变化趋势与活动层厚度的变化趋势是一致的。4种不同强迫模拟的地表温度差异主要是由于强迫数据中2 m气温的差异造成的，因此我们分析了2 m的气温变化。从图6可以看出，2 m气温变化趋势基本为正值，表现出增加的趋势，也就是说2 m气温整体呈现出增加的趋势，变化趋势分别为0.036℃/a、0.035℃/a、0.035℃/a和0.054℃/a，4组模拟的平均趋势为0.040℃/a。除青藏高原的部分区域外，2 m气温以及地表温度及活动层厚度的变化趋势是一致的。

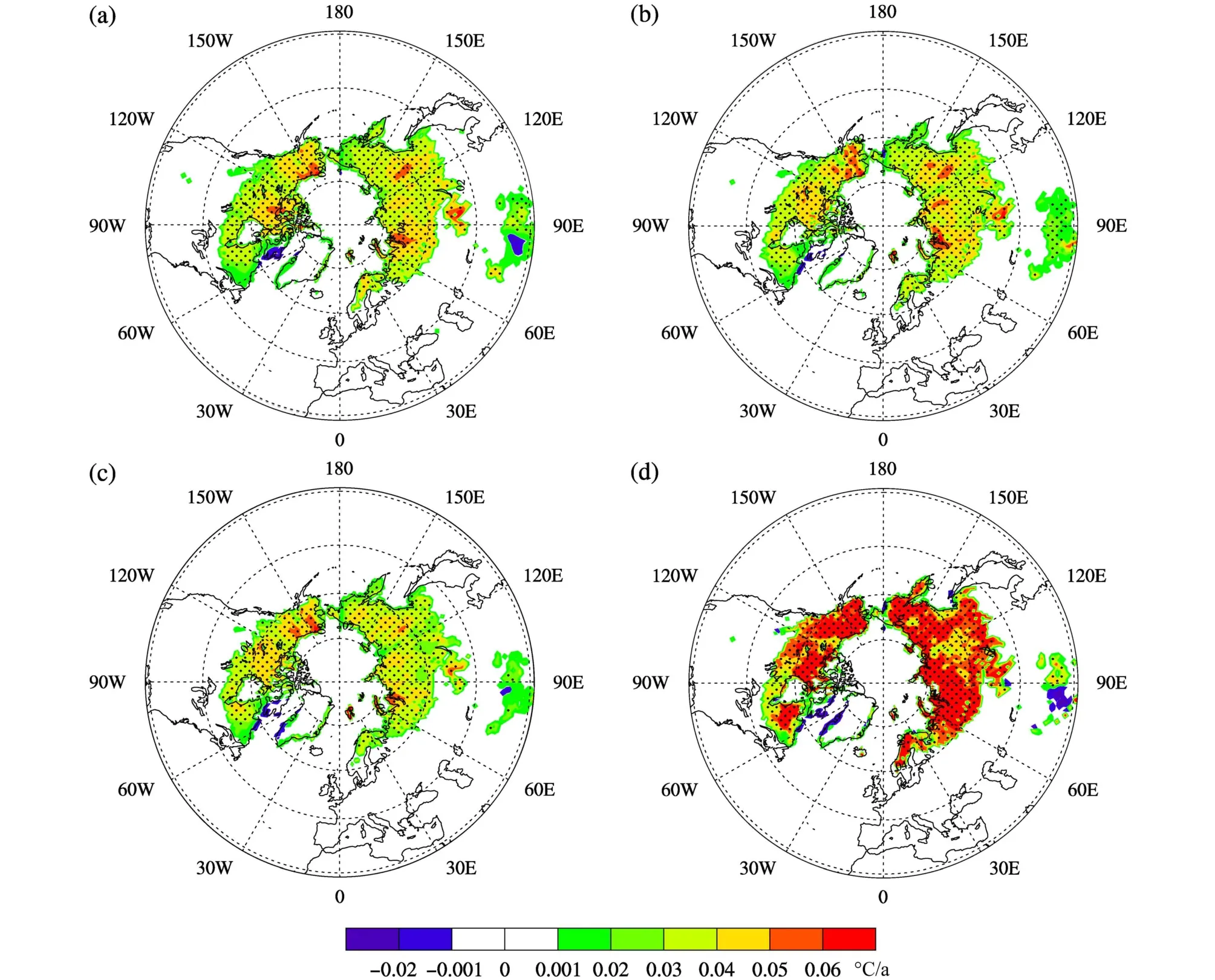
图5 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年地表温度变化趋势Fig. 5 Simulated ground temperature trends (℃/a) using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c) Princeton, and (d) WFDEI during 1960–2009

图7模拟的是1960～2009年多年冻土区2 m气温与活动层厚度年际变化，从图中可以看出，2 m气温的变化趋势与活动层厚度变化趋势显著相关，相关系数分别为0.82、0.83、0.73、0.87。随着气温的升高，活动层厚度表现出增加的趋势。表明活动层厚度的模拟与2 m气温有很强的相关性。图8模拟的是1960～2009年多年冻土区2 m气温变化趋势与活动层厚度变化趋势相关系数的空间分布。从相关系数的空间分布上可以看出，不同强迫下2 m气温变化趋势与活动层厚度变化趋势整体上显著相关，但不同的区域会有差异。俄罗斯东部和西部、加拿大东部等地区均呈现出较高的相关性，说明这些地区活动层厚度模拟受气温影响较大。俄罗斯中部以及阿拉斯加地区相关性较低，说明这些地区除了气温影响外，同时海拔、活动层岩性、含水特征以及影响地面温度变化进程的地形特征和下垫面性质等也对活动层厚度模拟影响较大。在陆面模式中可表示为土壤性质、模式参数、物理参数化方案等对活动层厚度模拟的影响，具体区域还需要结合观测数据进一步进行研究。总体来看，强迫数据中2 m气温对于活动层厚度模拟的影响还是占主要因素。

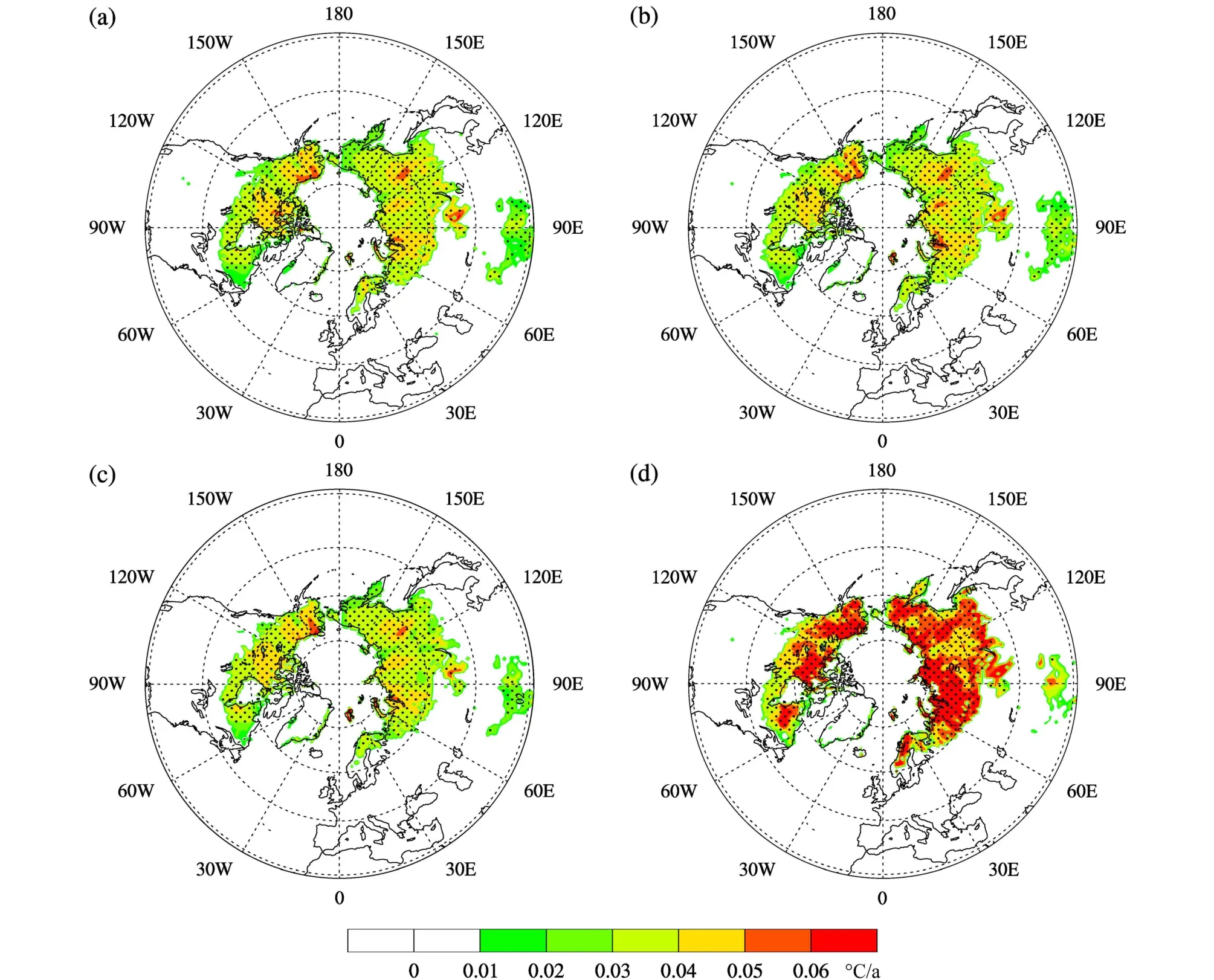
图6 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年 2 m 气温变化趋势Fig. 6 Simulated 2-m air temperature trends (℃/a) using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c) Princeton, and (d) WFDEI during 1960–2009

4 讨论与结论

本研究主要是在不同大气强迫作用下，对陆面模式CAS-LSM模拟的多年冻土活动层厚度进行评估。分别采用4种不同的大气强迫数据（SWP3、CRU-NCEP、Princeton、WFDEI）驱动CAS-LSM，并分析不同强迫下的活动层厚度空间分布及变化趋势。通过与CALM活动层的观测数据比较，CASLSM模拟得到的活动层厚度与观测值接近较为一致，但表现出偏大的趋势。主要是由于Stenfan公式在计算活动层厚度时，假设吸收的热量全部用于多年冻土的融化，忽略了土壤本身温度变化的感热影响（Jumikis, 1978; Woo et al., 2004），因此造成了模拟结果偏大。由于地表温度是形成多年冻土的关键因素，Stefan利用地表温度来计算单层土柱冻融深度。不同强迫模拟地表温度的不同会造成活动层厚度模拟的差异，而地表温度模拟的差异主要是由于强迫数据中的2 m气温的差异造成的。通过对图3、5、6的分析表明：总体来看，除青藏高原的部分区域外，2 m气温以及地表温度的变化趋势与活动层厚度的变化趋势是一致的。青藏高原的部分区域出现了活动层厚度变薄、地表温度降低的趋势而2 m气温是增加的。这可能由于陆面模式在该地区的地表参数、物理参数化方案等造成的，具体还需要针对这一地区结合观测数据进行深入研究。

对于不同强迫造成的活动层厚度相对变化的不确定性，我们首先计算活动层厚度的相对变化，定义为t年活动层厚度，年到年的活动层厚度变化趋势为，那么年相对于年活动层厚度的相对变化：

那么2009年相对于1960年的活动层厚度相对变化：

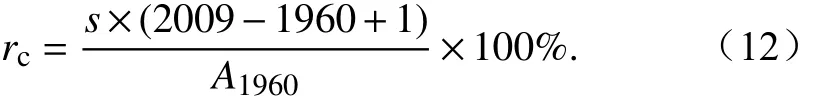
不同强迫造成的活动层厚度相对变化的不确定性范围是基于不同强迫数据模拟相对变化的标准差求得的。从活动层厚度区域平均上，4种强迫模拟的活动层厚度相对变化分别为11.2%、13.5%、10.3%、23.5%，不确定性范围为14.6%±6.1%。图9模拟的是多年冻土区活动层厚度在不同强迫下相对变化标准差的空间分布，标准差越大说明不同强迫对于本地区的模拟差异越大，不确定性越大。这些地区的强迫数据对于活动层厚度相对变化的模拟影响越大。从图9中可以看出在青藏高原、俄罗斯的西部地区、阿拉斯加地区等地区差异较大。因此这些地区的不确定性范围也较大，在这些地区不同强迫对于活动层厚度相对变化模拟影响也较大。

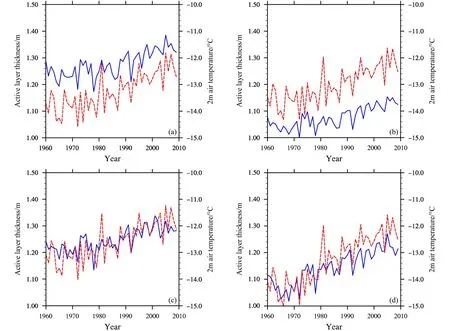
图7 （a）CRU-NCEP、（b）GSWP3、（c）Princeton、（d）WFDEI 4 组大气强迫数据模拟的 1960～2009 年多年冻土区 2 m 气温（红线）与活动层厚度（蓝线）年际变化趋势Fig. 7 Simulated interannual trends of 2-m air temperature (red line) and active layer thickness (blue line) using four atmosphere forcing data (a)CRU-NCEP, (b) GSWP3, (c) Princeton, and (d) WFDEI during 1960–2009

本研究的主要结论如下：

（1）通过与多年冻土区活动层厚度的观测数据以及土壤温度插值得到的结果比较，CAS-LSM模拟的结果与观测值比较接近。基于WFDEI模拟的活动层厚度要优于其他3种强迫数据模拟的。

（2）对于不同强迫造成的活动层厚度模拟的差异，主要原因是由于强迫数据中2 m气温的差异造成的。2 m气温的差异造成模拟的地表温度不同，从而导致活动层厚度模拟的差异。通过分析表明：除青藏高原的部分区域外，活动层厚度的变化趋势与地表温度以及2 m气温变化趋势是一致的。总体来看，强迫数据中2 m气温对于活动层厚度模拟的影响还是占主要因素。不同大气强迫模拟的活动层厚度区域平均和变化趋势范围分别为1.1～1.25 m和 0.27～0.51 cm/a。

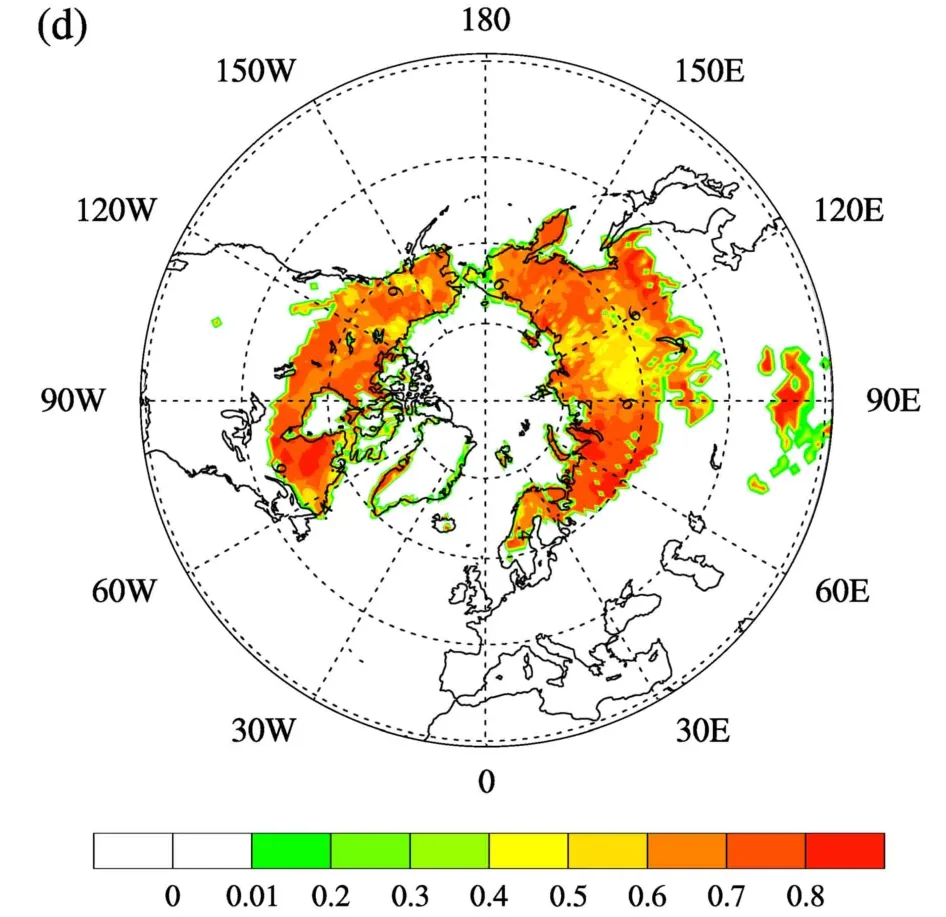
图8 （ a） CRU-NCEP、（ b） GSWP3、（ c） Princeton、（ d）WFDEI 4组大气强迫数据模拟的1960～2009年多年冻土区2 m气温与活动层厚度相关系数的空间分布Fig. 8 Spatial distribution of correlation coefficients between simulated 2-m air temperature and simulated active layer thickness using four atmosphere forcing data (a) CRU-NCEP, (b) GSWP3, (c)Princeton, and (d) WFDEI during 1960–2009

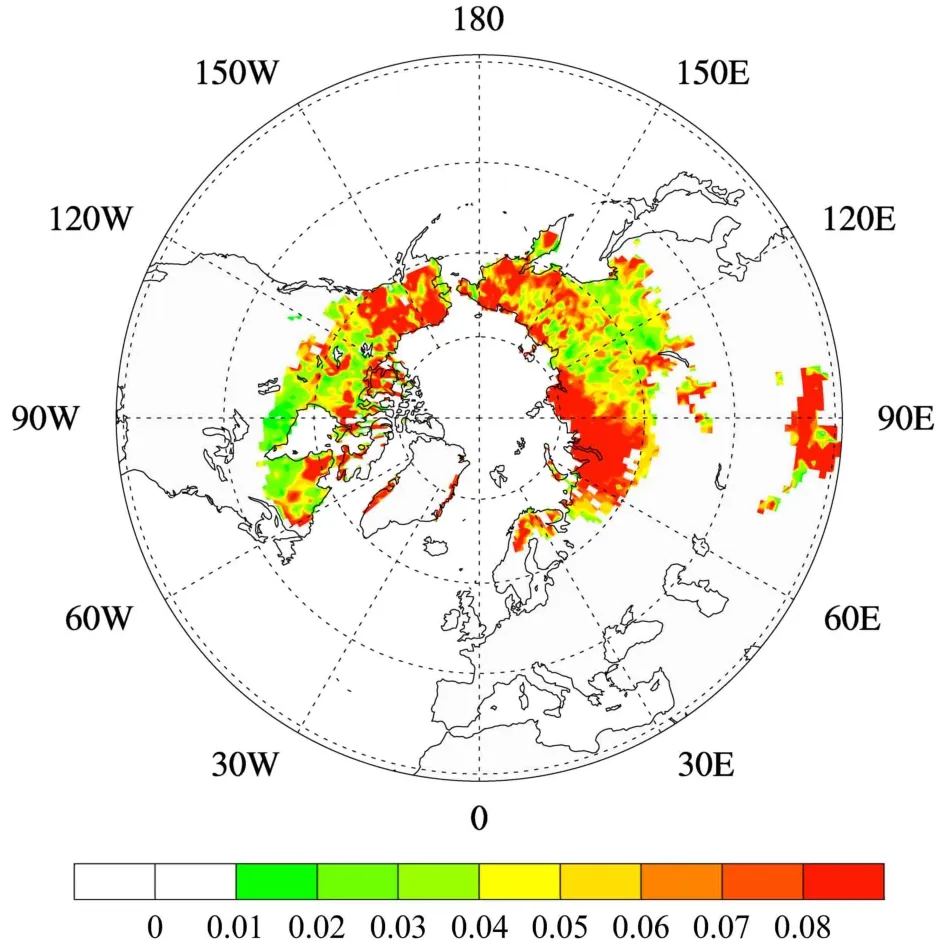
图9 多年冻土区活动层厚度在不同强迫下相对变化标准差的空间分布Fig. 9 Spatial distribution of relative variation standard deviation of active layer thickness in permafrost under different forces data

（3）不同强迫数据模拟的活动层厚度变化趋势与2 m气温变化趋势整体上相关，但不同的区域会有差异。同时不同强迫数据对于模拟活动层厚度相对变化的影响较大。模拟的活动层厚度相对变化分别为 11.2%、13.5%、10.3%和23.5%，不确定性范围为14.6%±6.1%。在青藏高原、俄罗斯的西部地区、阿拉斯加地区等地区的不确定性范围较大，在这些地区不同强迫对于活动层厚度相对变化模拟影较大。