一种改进的免缩放坐标旋转数字计算算法及其实现

2021-02-24马忠松

科学技术与工程 2021年1期

薛原，马忠松

(1.中国科学院太空应用重点实验室，中国科学院空间应用工程与技术中心，北京 100094；2.中国科学院大学中国科学院空间应用工程与技术中心,北京 100094)

相比传统的查找表方法，经典坐标旋转数字计算(coordinate rotation digital computer,CORDIC)算法因其具有实现精度可控，资源占用较少等优点已经被广泛应用在傅里叶变换、矩阵分解、方程求根、频率合成等信号处理模块中[1-6]。虽然经典CORDIC算法可以通过简单的移位和加减法操作实现复杂函数求值的功能，但因该算法存在迭代次数过多和需要进行缩放因子补偿等缺点，使得其在高速低延时等场景下的应用受到了一定的限制。

近年来，对经典CORDIC算法进行改进成为中外学者研究的热点问题[7-13]。文献[7]提出了基于小容量查找表的CORDIC算法设计，减少了迭代级数，但却需要复杂的校正模块进行补偿，且算法扩展性较差。文献[8]采用了最佳一致逼近方法来提高计算精度，但对于经典CORDIC算法的迭代结构并未做大的改进。文献[9]采用了角度重编码和合并迭代的方法来减少延时，但其硬件资源消耗较大。文献[10-11]均提出了使用查找表来减少冗余迭代的思路，在一定程度上减少了迭代次数，但其预处理模块却又过于复杂。文献[12]采用了不同的基旋转角度集，并对CORDIC迭代单元做出了改进，节省了一定的硬件资源，但仍然需要较多的迭代次数。文献[13]提出了将两次迭代简化为一次旋转操作的方法，并且不需要进行缩放因子补偿，但其迭代结构随迭代次数而变化，给硬件实现带来了一定困难。

在文献[13]的基础上，现提出一种效果更好的改进免缩放坐标旋转数字计算算法，该算法对折叠后的坐标平面进行细分，通过建立查找表来达到减少平均迭代次数和硬件资源消耗的目的，且计算精度也有一定的提高，具有相应的工程应用价值。

1 相关算法原理分析

1.1 经典CORDIC算法原理分析

经典CORDIC算法的理论基础为如图1所示的吉文斯旋转，其在平面直角坐标系中的公式[14]为

(1)

式(1)中：[x0y0]T为初始向量；[xθyθ]T为目标向量；θ为在逆时针方向下从初始向量旋转到目标向量所需的旋转角度。

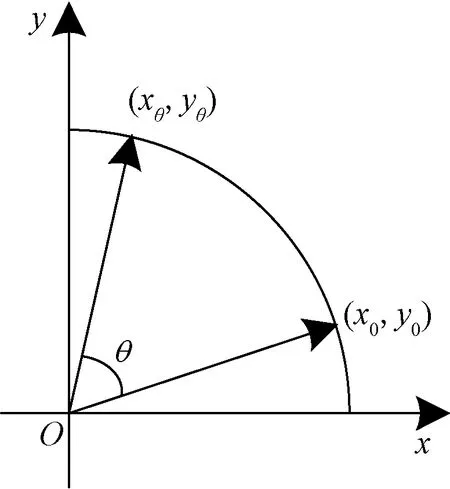
图1 吉文斯向量旋转Fig.1 Givens vector rotation

经典CORDIC算法在此基础上，用累加一组基旋转角度(θi)的方式来逐次逼近所求角度θ，若取θi=tan-1(2-i)，经典CORDIC迭代公式可写为

σi=sgn[z[i]]

(2)

(3)

z[i+1]=z[i]-σitan-1(2-i)

(4)

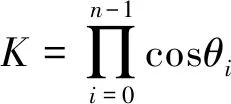
(5)

式(5)中：n为迭代次数。显然缩放因子产生的影响可以通过补偿模块来消除。此外，经典CORDIC算法可计算的角度上限θCORDIC_max由式(6)给出：

(6)

1.2 VSF CORDIC算法原理分析

免缩放因子CORDIC算法(virtually scaling free CORDIC,VSF CORDIC)是一种性能优异的改进CORDIC算法[13]。其针对经典CORDIC算法中存在较多冗余迭代的问题，提出了优化基旋转角度取值和跳跃式旋转的改进方案，并结合泰勒展开定理,将经典CORDIC算法中的迭代公式优化为

(7)

由方程(7)可知，VSF CORDIC算法首先将基旋转角度取值改为θi=2-i，此外σi取值范围也变为{0,1}，依据每次迭代是否被跳过而取值。显然，这些改动会引起补偿因子的不确定性和相应的近似误差。但可以证明[13]，在满足不等式(8)时，采用VSF CORDIC算法引入的计算误差在机器字长为N的定点实现过程中可以被忽略，且相应的补偿因子也可以被视为1而不影响计算精度。

(8)

由于文献[8]中并未给出使用θi=tan-1(2-i)作为基旋转角度的精度保持条件，故经过相应推导，得到与不等式(8)对应的约束条件为

(9)

尽管VSF CORDIC算法提供了一种高效的简化计算方法，但在不等式(8)的约束下，其可计算的角度上限由式(10)给出，即

(10)

在不同位宽条件下，根据式(6)和式(10)可以计算出CORDIC算法和VSF CORDIC算法的收敛域，如表1所示。

综上，经典CORDIC算法虽然收敛域较大，但其迭代过程过于冗余。VSF CORDIC算法虽然可以减少迭代次数且不需要缩放因子补偿，但由表1可知其主要缺点为适用角度范围过小，因而无法满足大部分实际场景的需求。

表1 不同CORDIC算法的收敛域Table 1 ROC of different CORDIC algorithm

2 改进算法方案与实现结构

2.1 VSF CORDIC算法改进分析

文献[13]中提出的双步迭代思想本质上是VSF CORDIC算法的一种应用，虽然减少了迭代次数，但因其迭代结构会随着迭代次数而改变，所以不易在硬件平台中实现。因此在文献[9-10]的基础上将VSF CORDIC算法的迭代结构细分为两级。第一级按照式(7)所示进行移位和相加计算，当迭代次数满足条件i≥N/2时，可以采用如图2所示的第二级改进结构进行计算，该结构免去了一级移位和相加模块，在简化迭代单元的同时能够保持计算精度。而且采用确定的两步迭代结构，既能够降低硬件实现的难度，又可以通过插入流水线的方式来提高系统运行速度。此外，在采用Q31/Q63等高精度格式进行硬件实现时，图2结构能更加明显地减少硬件资源消耗。

2.2 角度折叠方案改进分析

目前，扩展VSF CORDIC算法收敛域的主要方法是通过区域折叠将输入角度映射到收敛范围内，主要分为8区域折叠[13]和16区域折叠[9]两种方案。8区域折叠方案划分区域少，且判别模块和补偿模块简单，但划分区域间隔大，后续算法复杂。16区域折叠方案划分区域间隔小，后续算法简单，但判别模块和补偿模块较为复杂。文献[13]采用8区域折叠方案对其算法的收敛域进行扩展，但并未给出具体的映射结构。

由式(8)可推导出Q14格式下的VSF CORDIC算法的收敛域可以扩展到7.158°，其相比Q15格式下的3.579°有较大提升。且Q15和Q14格式下可表示的角度精度均在10-5rad量级，也远远优于文献[13]中采用的10-3rad量级。此外，在Q14格式下，当迭代次数i≥7时，即可采用图2所示的简化结构，相比Q15格式下更为简单。因此，若在Q14格式下采用8区域折叠方案，后续可以采用如图3所示的区域细分方案来完成剩余的处理工作，其细分间隔为tan-1(2-i)，显然小于Q14格式下的VSF CORDIC算法收敛域，因此经过细分后的角度可以直接使用VSF CORDIC算法进行计算。

2.3 改进算法实现结构

综上，这种结合区间细分和查找表方法的改进VSF CORDIC算法的实现结构如图4所示，其中输入角度为范围在[0,2π)内Q14格式下的18位无符号数，输出为相应的16位有符号三角函数值。预处理和后处理模块主要进行角度映射和解映射操作，其映射公式如表2所示。判决模块主要进行细分区间判别工作，经判决后的角度减去相应的起始角度后，即可和相应查找表内的起始向量(16 bit)送入后级模块进行计算，查找表的构建方法如表3所示。

表2 角度映射方程Table 2 Mapping equation of the input angles

表3 查找表模块Table 3 Look-up table module

3 仿真结果与分析

为了验证改进算法的可行性，在MATLAB平台上按照图4所示的结构对该改进算法进行了仿真建模，并在区间[0,π/4)以0.00 006 rad为间隔产生了一组测试角度。将其输入所搭建的仿真模型可以得到如图5、图6所示的输出结果，其中图5给出了每个测试角度所需要的迭代次数，图6给出了对应输出结果的计算误差起始位数。

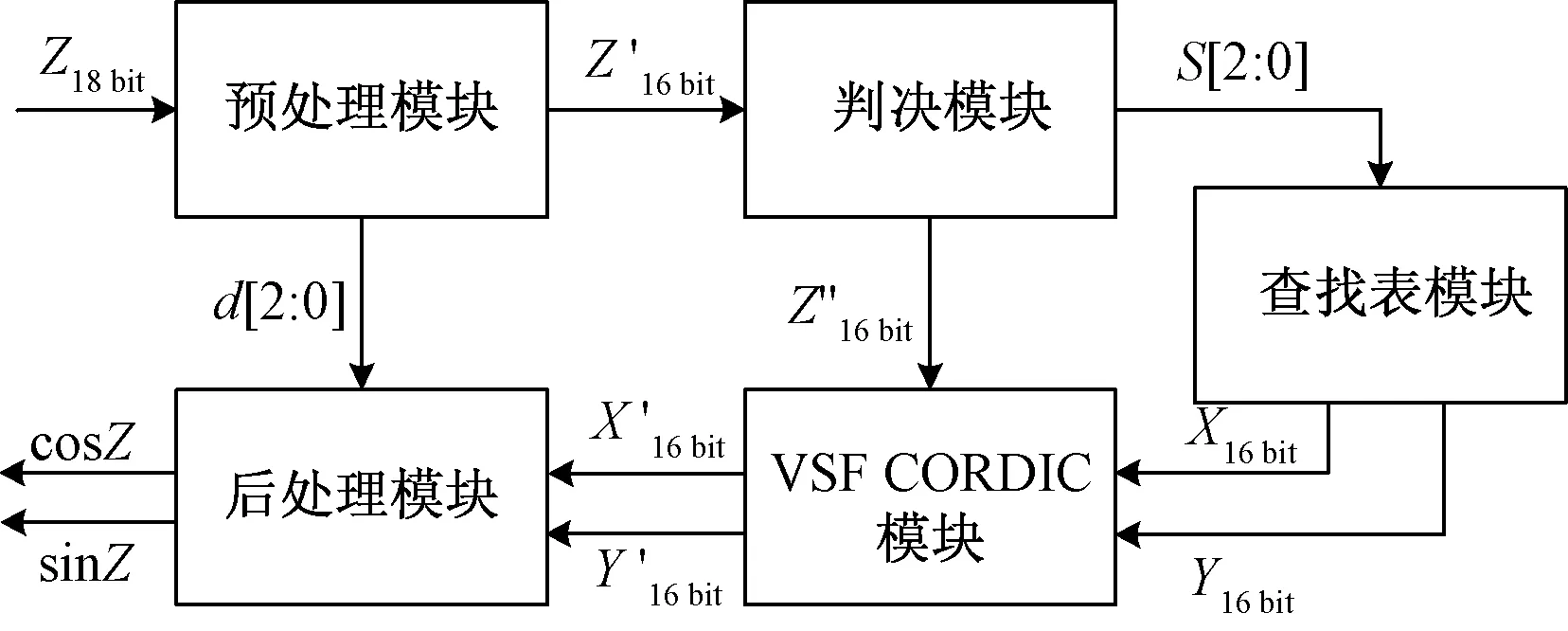
图4 改进算法实现架构Fig.4 Architecture of the improved method

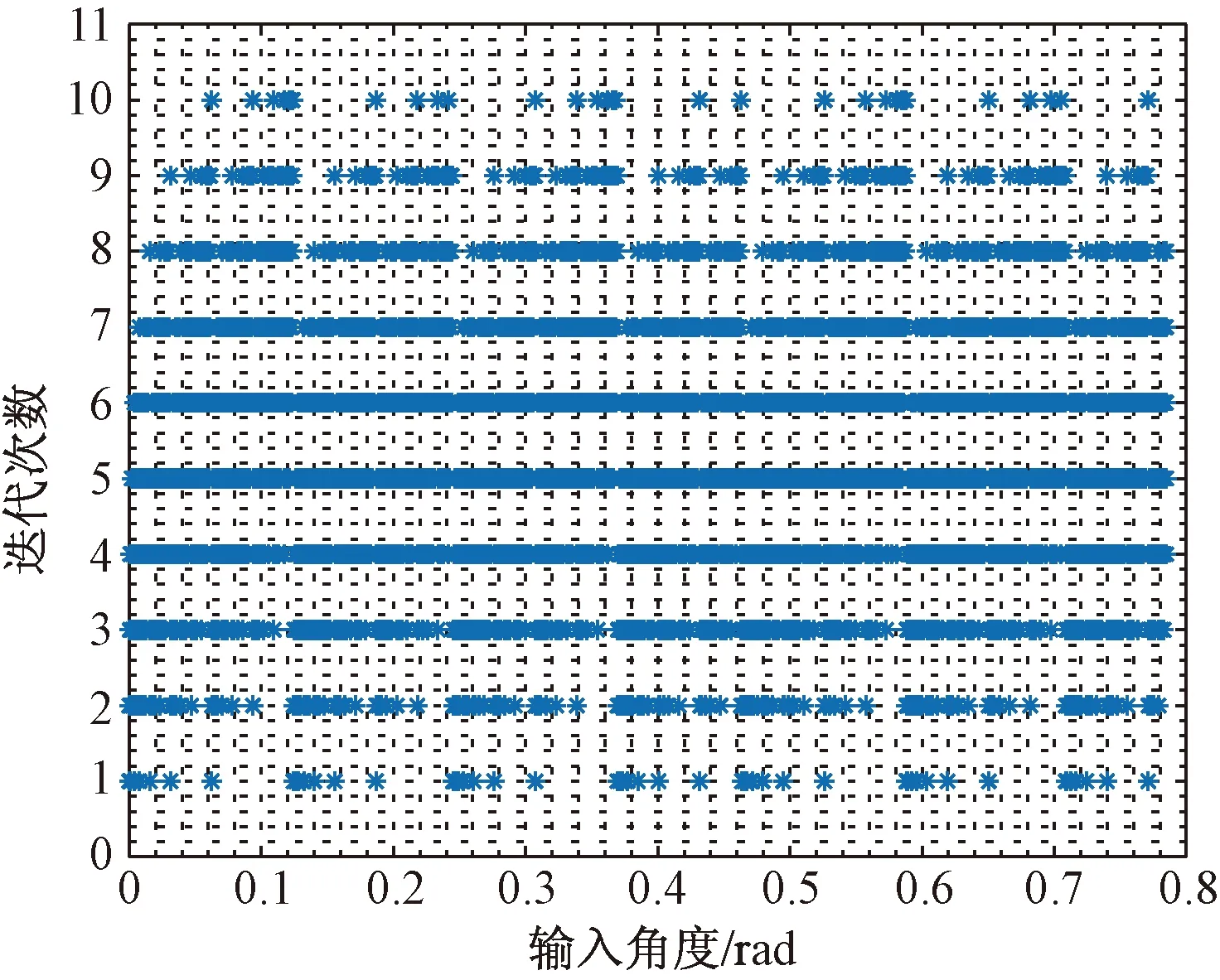
图5 迭代次数仿真结果Fig.5 Number of iterations of the improved method

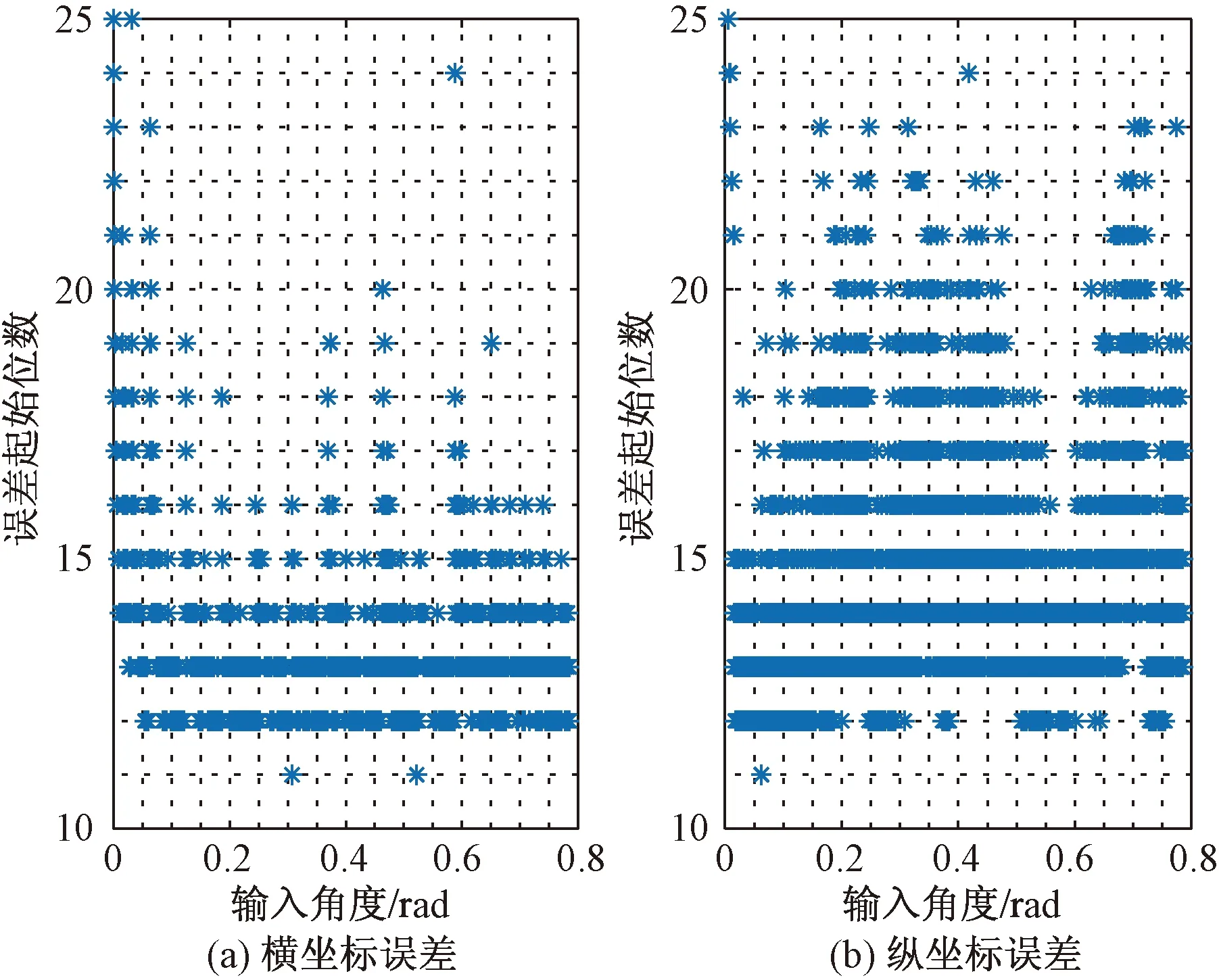
图6 计算误差仿真结果Fig.6 Numerical errors of the improved method

为了便于和已有算法进行对比，在表4中列出了部分已有主流算法的平均迭代次数，其数据由文献[13]给出。由仿真结果可知，在16位精度下改进算法的平均迭代次数仅为经典算法的1/3，比文献[13]改进算法的平均迭代次数也下降了10%，较已有的其他主流改进算法也有不同程度的下降。此外，该改进算法的误差最大起始位数出现在第11位，也优于文献[13]中所提出的改进算法。综上，本文算法在减少平均迭代次数和误差精度控制方面均有较好的效果。

表4 平均迭代次数比较Table 4 Comparison of the number of iterations

4 FPGA实现与验证

依据前文给出的实现流程，在Quartus Prime软件上完成了相应的Verilog代码开发，并将其配置在Altera (Intel) Cyclone Ⅳ 系列的现场可编程门阵列(field programmable gate array,FPGA)上，最终在Modelsim平台上得到仿真结果如图7所示。在表5中列出不同算法的资源消耗进行对比，由于文献[13]并未给出其改进算法所消耗的硬件资源，因此表5中没有列出。但其在未插入流水线的情况下，所消耗的硬件资源为VSF CORDIC算法的两倍以上[13]。因此，本文算法在硬件资源消耗方面均优于经典CORDIC算法和文献[13]所提出的改进算法。