应用反向传播神经网络算法的发动机动态总压畸变预测

赵海刚, 任丁丁, 王俊琦

(中国航空工业集团公司, 中国飞行试验研究院发动机所， 西安 710089)

现代先进战斗机要求高亚音速和跨音速飞行机动性、超机动性，由此引起进气道流场的严重分离，进气道与发动机气动截面上大范围高强度的动态气流畸变，这种动态气流畸变显著地影响发动机压缩系统的气动稳定性[1]，稳定性的评估需要建立动态气流畸变的评价体系[2-3]。要研究进气道的动态气流畸变对发动机压缩系统气动稳定性的影响，首先必须要确定在关键的飞行条件下气动截面上总压随时间的变化关系；其次，在此基础上寻找最大瞬时畸变。最大瞬时畸变的预测方法可以分为两类：确定性方法[4]和畸变合成法。

在20世纪70～80年代，不少学者提出了畸变合成法对动态畸变进行预测，基本方法有：①由测量的紊流度和随机数合成脉动总压；②脉动总压加稳态总压得动态总压；③根据每一个测点的动态总压寻找最大瞬时畸变和相应的图谱。比如Jacocks法[5]、Motycka法[6]、Stevens法[7]和Sedlock改进的统计预测方法[8]等。从已发表的论文来看，中国只有西北工业大学的吴虎等[9-10]、刘胜[11]，南京航空航天大学的梁德旺等[12-14]对于预测动态总压最大瞬时畸变做过一定的理论研究，但是无论是在飞机/推进系统设计的任何阶段，都没有应用该方法做过最大瞬时动态总压畸变的预测，在飞行试验中，也多是采用俄罗斯的综合畸变指数来评价动态总压畸变。到了20世纪90年代，出现了将计算流体力学(computational fluid dynamics, CFD)预测方法应用于动态畸变预测的方法，即综合CFD与畸变合成法，这种方法仅需要定常的CFD计算以及少量的试验便可以完成对动态畸变的预测，有依赖试验少、耗资极小、可靠性较高的优点。

综合CFD与畸变合成法与传统的畸变合成法的区别在于：传统的畸变合成法中紊流度和稳态总压都是由试验测得的，而综合CFD与畸变合成法中紊流信息和稳态总压都是由CFD计算所得的。综合CFD与畸变合成法中得到的是紊流信息，而不是畸变合成所需要的紊流度，因此必须采用紊流相关将紊流信息转化为紊流度，而紊流相关正是综合CFD与畸变合成法中的关键部分，紊流相关直接关系到相关系数的获取和利用CFD方法预测动态总压畸变的准确性。

现通过改进紊流相关中的算法，旨在提高动态总压畸变预测的准确性。

1 综合CFD与畸变合成法

综合CFD与畸变合成法的流程图如图1所示。图1中的紊流计算结果和多点稳态总压都是由CFD计算所得的，紊流相关利用试验点的数据所得到的紊流度和对应试验点的CFD计算数据得到紊流信息和紊流度之间的相关性，然后通过得到的紊流度和由计算机产生的随机数来合成脉动总压，脉动总压与CFD计算出的稳态总压相叠加得到动态总压，在此基础上寻找出最大瞬时畸变和相应的图谱。然后通过设置不同的随机数多次重复计算来获得一个平均畸变峰值图谱，再将所有测点的压力峰值进行平均得到可能的最大压力畸变图谱。

图1 综合CFD与畸变合成法流程图Fig.1 Procedure of CFD-distortion synthesis method

现重点关注从紊流计算结果到多点紊流度过程中的紊流相关法。

进气道紊流度ε是由脉动总压的均方根与该测点稳态总压的比值表示的，即

(1)

流体动力学中，三个方向上平均速度脉动是通过湍动能k体现的，其数学表达式为

(2)

因此可以认为紊流度ε和湍动能k之间是存在某种关联的。

另外，稳态总压是瞬时总压的组成部分，应该考虑成对紊流度有贡献的项；轴向速度是引起脉动总压迁移的因素，也应该考虑成对紊流度有贡献的项；采集的压力信号可能含有噪声(尽管滤波已消除了噪声的影响)，与声场有关的声速也应该考虑；考虑到流体的压缩性，密度是不可少的[15]。至此，对紊流度有贡献的项共有5个，分别是湍动能k、稳态总压P*、轴向速度u、声速a、密度ρ。

湍动能、稳态总压、轴向速度、声速、密度与紊流度之间可以表示为

ε=f(u,a,k,ρ,P*)

(3)

通过量纲分析，得到紊流度的表达式为

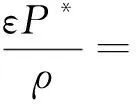
(4)

式(4)中：C1、C2、C3、C4是需要确定的常数。

式(4)是一个非线性方程，美国在F/A-18A HARV研究中将式(4)线性化，线性化的过程是将贡献较小的一、二、三项去掉，只保留贡献较大的第四项[15-16]，得

(5)

式(5)中：C为需要确定的系数；γ为流体的重度；g为流体的重力加速度。

从而可以采用最小二乘法对系数C进行确定。

从上述方法可以看出紊流度确实是与稳态总压、轴向速度、湍动能、声速、密度5个量有关，并且这种关系是复杂的非线性关系。将非线性的关系简化为线性必然会带来误差。

2 BP神经网络

2.1 基本思想

人工神经网络是人脑及其活动的一个理论化的数学模型，它由大量处理单元(神经元)通过适当方式互联构成，是一个大规模的非线性自适应系统，它具有通过学习获取知识的能力，并将获取的知识存储在连接权中。人工神经网络技术目前在航空领域已得到了广泛应用[17-20]。反向传播神经网络(back propagation artificial neural networks,BPANN)是一种典型的多层前向人工神经网络，由于采用反向传播(BP)算法而得名。据统计，80%～90%的神经网络模型采用了BP网络或者它的变化形式，BP网络是前向网络的核心，体现了神经网络中最精华、最完美的内容。

BP算法是一种有导师的学习算法，其基本思想是学习过程可以由工作信号的正向传播与误差信号的反向传播组成。输入信号从输入层经隐层单元，传向输出层，在输出端产生输出信号，这是工作信号的正向传播。如果在输出层不能得到期望的输出，则转入误差信号反向传播。在误差信号反向传播的过程中，网络的权值由误差反馈进行调解。通过权值的不断修正使网络的实际输出更接近期望输出。

人工神经网络的处理方法一般分为两个步骤：①学习程序，对人工神经网络进行训练使其自主学习，训练流程如图2所示；②应用程序，是用训练后的网络对样本进行测试，从而完成预报功能，程序框图如图3所示。

图2 人工神经网络学习训练流程图Fig.2 Procedure of BPANN training

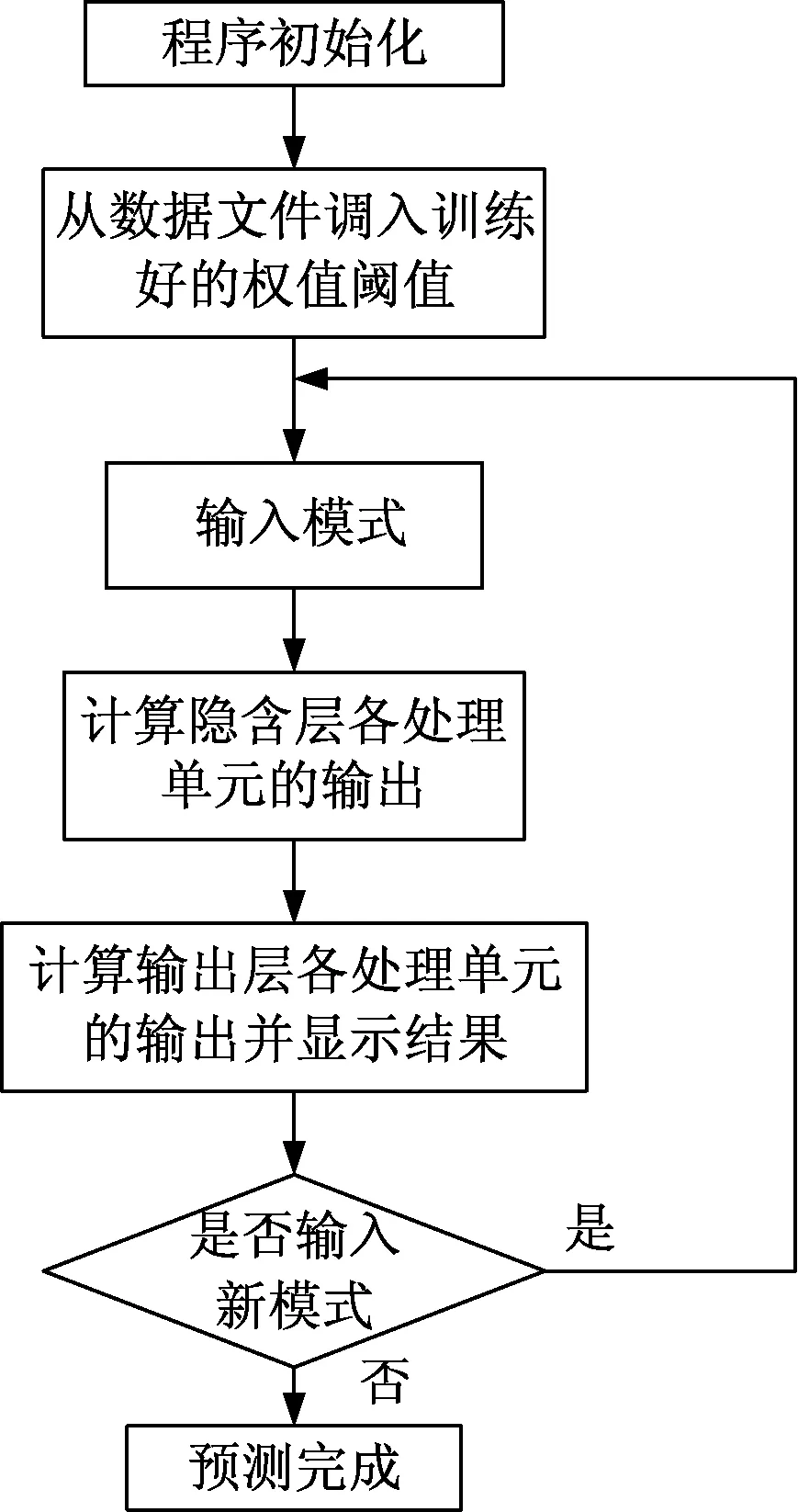
图3 人工神经网络预报流程图Fig.3 Procedure of BPANN prediction

式(4)是一个非线性问题，而且四个系数均不可知，另外该问题很还是一模糊问题，各项的表达式是否准确还不能确定，但是可以肯定的是紊流度ε与总压、密度、紊流动能、轴向速度、音速(P*、ρ、k、u、a)这5个参数有关系，因此采用非线性问题的解决思路是最好的办法。对于现研究对象，人工神经网络方法是一个很好的选择。

从结构上看，BP网络属于典型的前向网络，由输入层、输出层和若干隐含层组成，相邻两层的神经元之间形成全互连接，同层各神经元互不连接。典型的BP神经网络是由输入层、输出层和一个隐含层组成的三层网络，这也是最常用的一种BP神经网络，现阶采用的结构如图4所示。

图4 两层BP网络模型Fig.4 Two-layer BP ANN model

2.2 BP神经网络应用于总压畸变预测

采用综合CFD与畸变合成法来预测动态总压畸变时，需要在某一工况下，通过CFD计算获得进气道出口30个测点的湍动能、稳态总压、轴向速度、声速、密度，用这些数据推导相应测点的紊流度。是一个典型的非线性函数逼近问题，如式(4)所示，适宜采用BP神经网络进行求解。

取5个典型试验状态，得到这5个试验状态(在试飞中一个状态有30点紊流度ε的数据)的试验数据，再针对这5个状态进行相应的CFD计算，得到这5个状态每个测点位置的P*、ρ、k、u、a，则可得到如表1的150行样本数据。

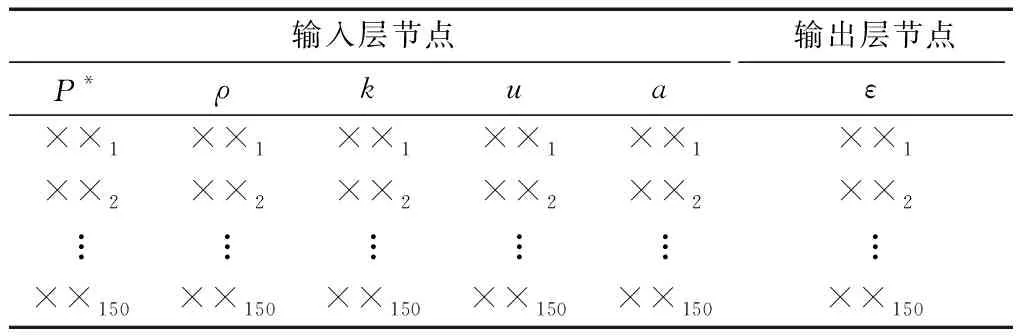
表1 样本数据Table 1 Sample data

用以上150行的样本数据进行网络的训练，网络达到给定的精度时，即网络训练完成以后，存储网络。接下来，就可以根据CFD计算结果预测紊流度ε，对于任何一个状态只需要进行CFD计算，得到30点测头位置的P*、ρ、k、u、a，将其代入训练好的网络，进行计算即可，其需要的输入数据以及最终输出的结果格式如表2所示。

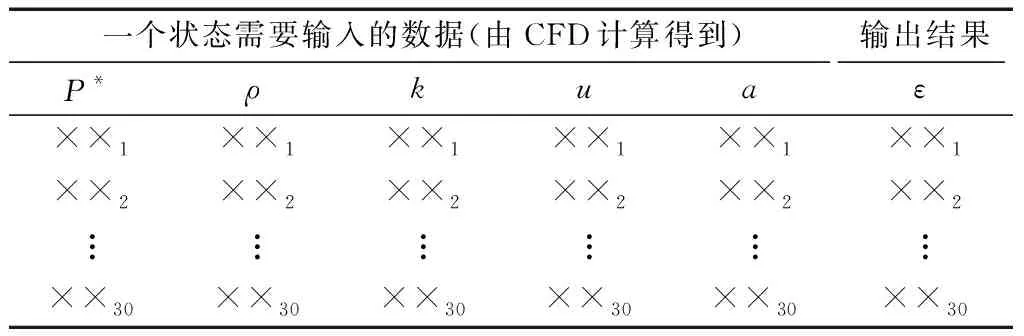
表2 紊流度预测Table 2 Turbulence prediction

经过上述步骤，紊流相关即可完成，没有简化计算公式，并全部考虑了P*、ρ、k、u、a对紊流度的影响。

以一腹部进气S弯进气道飞机10个工况的飞行试验数据为样本，飞行试验工况如表3所示。

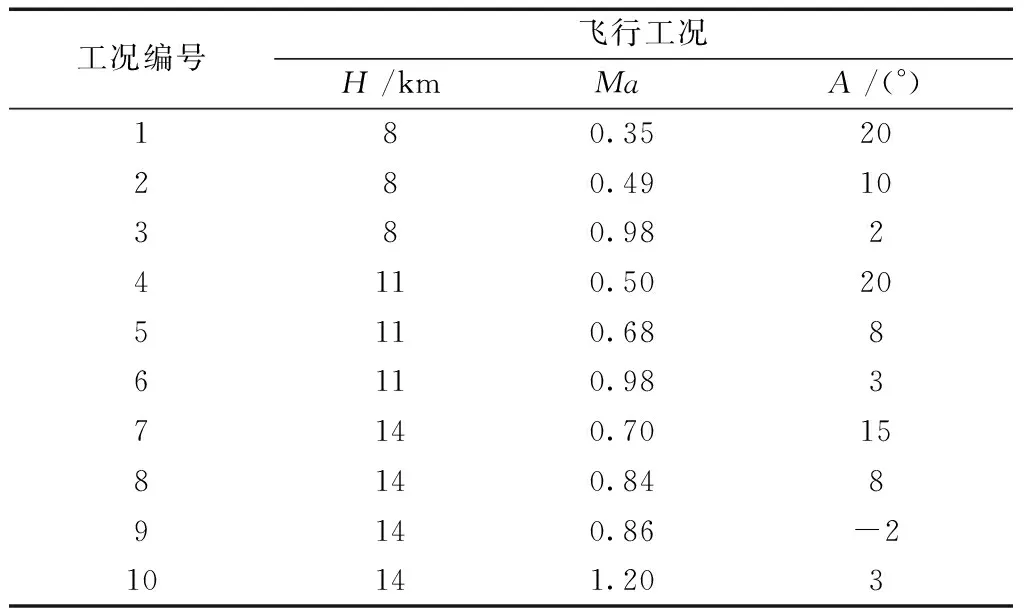
表3 飞行试验工况Table 3 Conditions of flight test

3 结果分析

3.1 各工况自我预测

对10个工况分别进行紊流相关研究，即对每个工况，先用30个测点作样本，获得系数C或者训练网络，然后再用这30个测点作为测试数据，得到预测的紊流度。

分别以工况1和工况6为例，得到了采用最小二乘法和BP神经网络法的预测紊流度和试验紊流度，各工况试验与计算紊流度对比图中横坐标为试验紊流度，纵坐标为计算紊流度，当试验值与计算值吻合时，所有的点应当分布在45°斜线上，点越集中于斜线附近，说明预测结果与试验结果越接近，如图5所示。可以看到，采用最小二乘法获得的紊流度，工况1中多数点基本分布于45°斜线附近，工况6中各点偏离45°斜线较远。而采用BP神经网络法获得的紊流度，工况1和工况6中各点几乎分布于45°斜线上，这说明预测的紊流度与试验紊流度几乎完全一致。

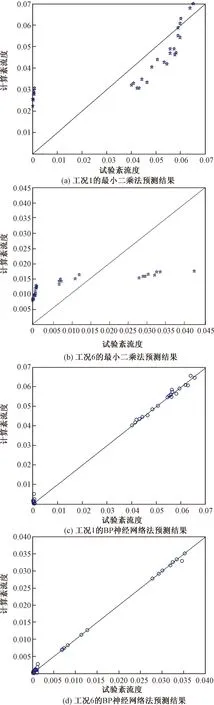
图5 自我预测结果对比Fig.5 Comparison of self-prediction results

表4比较了最小二乘法和BP网络法获得的平均紊流度，并且与试验结果进行了对比。从表4中看出BP网络法获得的平均紊流度与试验结果完全一致，最小二乘法获得的紊流度与试验结果有一定误差。

3.2 紊流相关预测紊流度

采用工况1、3、5、7、10作为样本，预测工况2、4、6、8、9的紊流度，如表4所示。分别采用最小二乘法和神经网络法预测各个工况紊流度，并且比较了两种方法的差别。

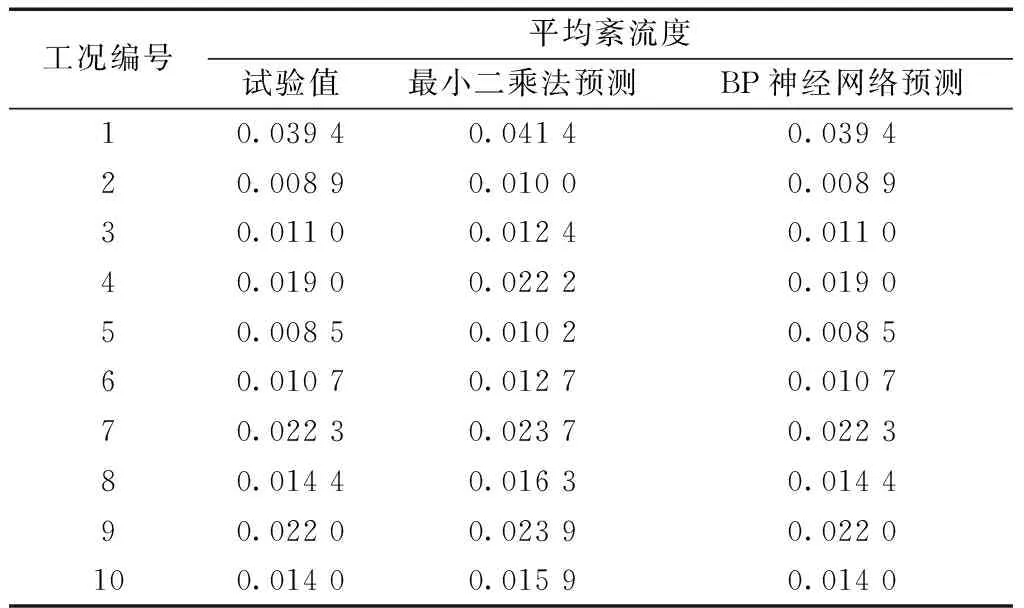
表4 平均紊流度比较

采用工况1、3、5、7、10为样本拟合的C值为0.589 8。图6(a)为采用最小二乘法预测的样本工况的紊流度，可以看出工况1和工况7预测值低于试验值，而工况3和工况10则高于试验值，工况5部分点吻合较好，其余点与试验值相比，则有高有低。图6(b)为预测的测试工况紊流度。可以看出，工况2、6、8、9部分点预测值与试验值吻合较好，其余点比试验值偏高；而工况4预测值与试验值吻合较差。

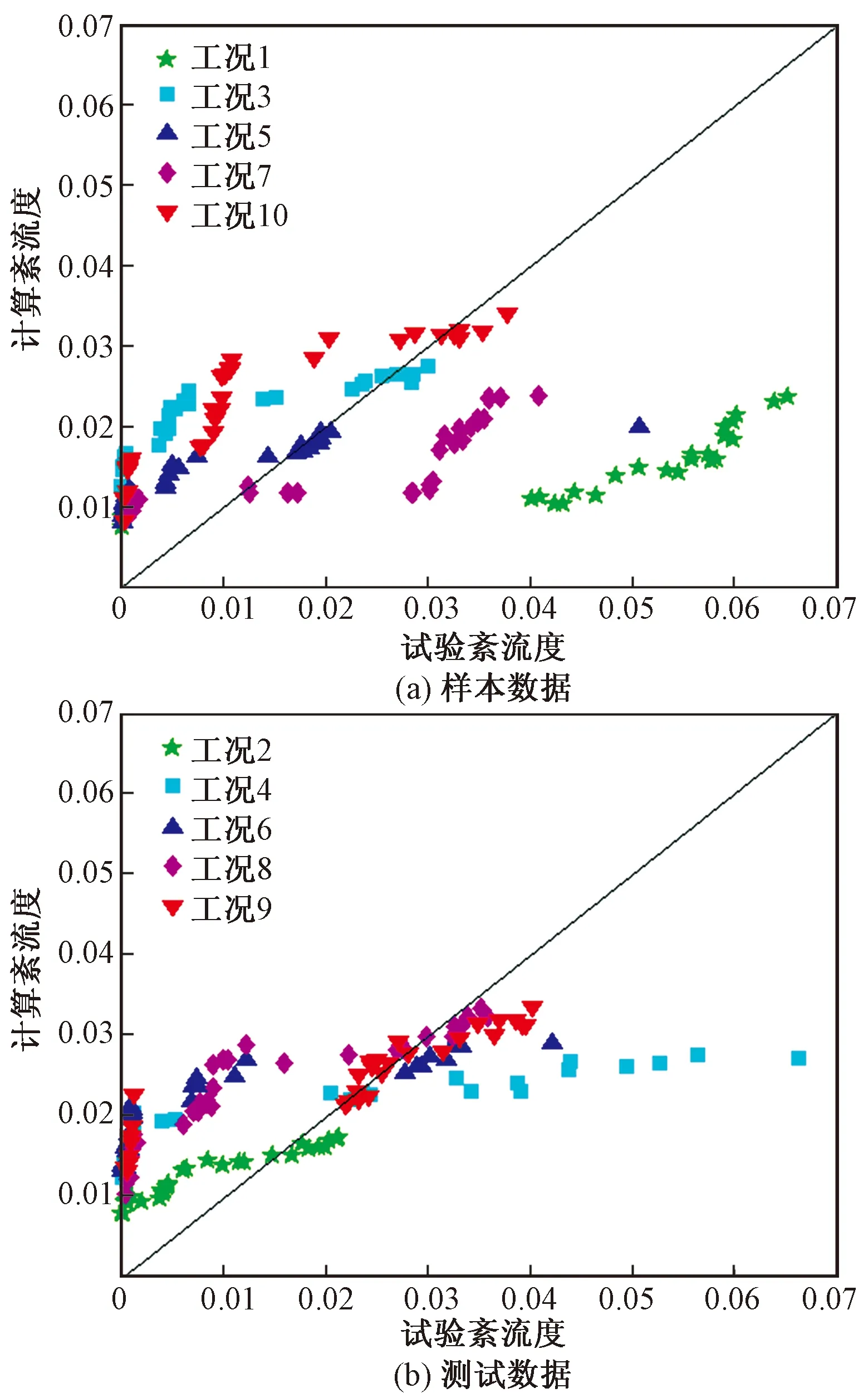
图6 最小二乘法紊流度预测结果Fig.6 Turbulence correlation results with least square method

采用工况1、3、5、7、10为样本训练网络，传递函数采用logsig和perline，隐含层采用10个神经元，输出层1个神经元。图7(a)为预测的样本工况紊流度，各工况数据点几乎分布于45°斜线两侧。图7(b)为预测的测试工况紊流度，各工况数据点虽然分布于45°斜线两侧，但是分布区域明显变大。

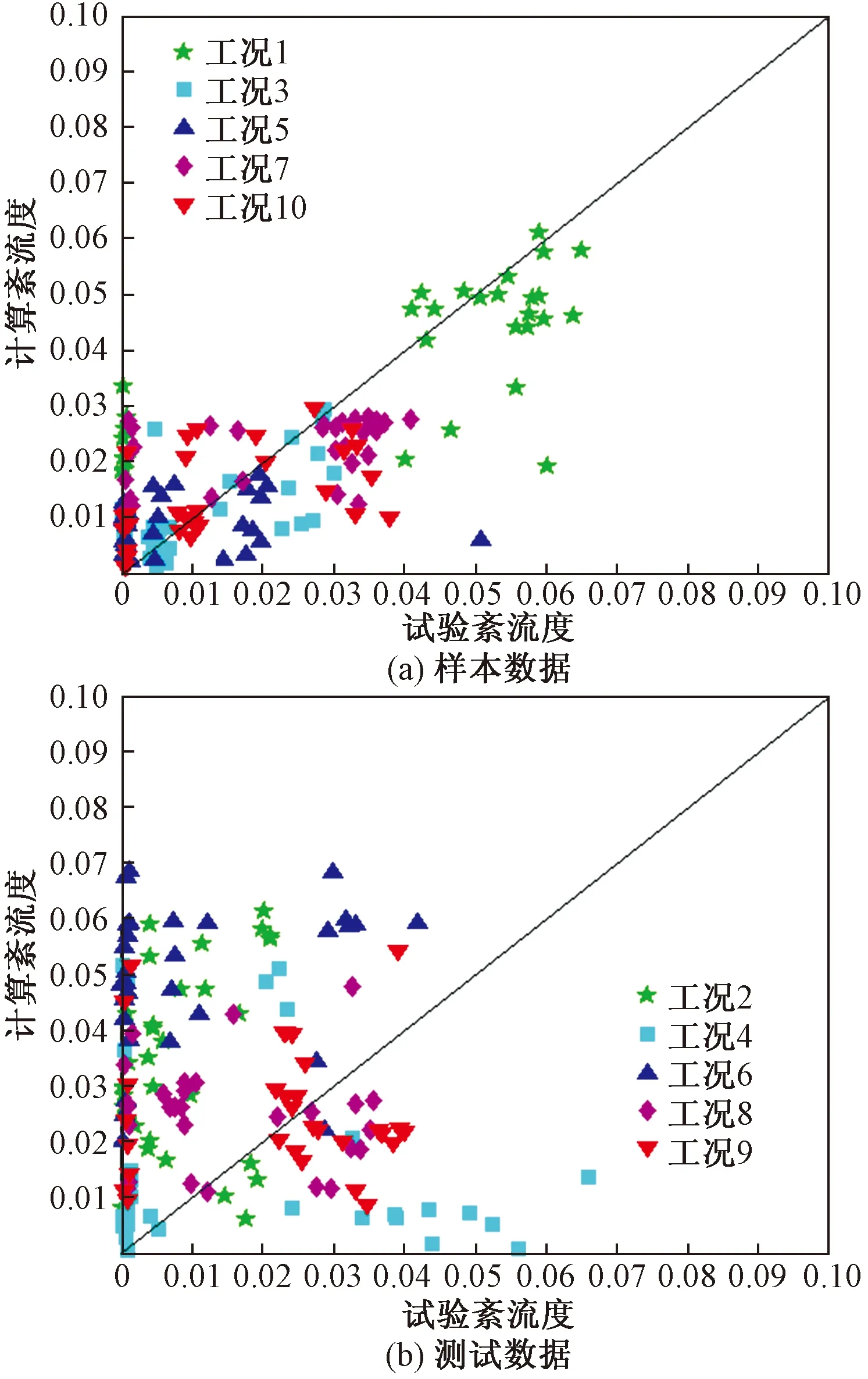
图7 BP神经网络法紊流度预测结果Fig.7 Turbulence correlation results with BPANN

比较了两种方法预测的平均紊流度，并与试验结果进行了对比，结果如表5所示。可以看出最小二乘法的预测结果与试验有一定差距；而BP网络方法预测的样本工况与试验吻合非常好，预测的测试工况中个别工况与试验差距较大，其余工况吻合较好，这说明网络的预测能力仍待提高，激活函数、神经元个数的选择等都会影响网络的预测能力，对于网络的训练仍需进一步研究。

表5 平均紊流度比较Table 5 Comparison of average turbulence

4 结论

(1)采用单个工况进行自我预测时，神经网络显示了良好的预测能力，预测结果与试验值吻合很好，点几乎分布于45°斜线上，平均紊流度预测值与试验值吻合尤其好，结果是一致的。

(2)采用最小二乘法，5个工况作为样本预测各工况紊流度时，预测的各个工况中的点较集中，测试工况的结果更接近45°斜线，样本工况的结果则偏离45°斜线较远，平均紊流度与试验值有一定的差距。

(3)采用BP神经网络法，5个工况作为样本预测各工况紊流度时，预测的各个工况中的点较分散，样本工况的结果较集中地分布于45°斜线两侧，测试工况的结果很分散，样本工况的平均紊流度与试验值一致，而测试工况中个别工况的平均紊流度与试验值有些偏差，网络的设置和训练需要进一步研究，以提高网络的预测能力。

(4)从预测结果看，神经网络法是一种更有前途的预测方法。