花朵授粉算法及其在断路器优化设计中的应用
2021-02-24夏克文石丽莉田芸贺贺紫平
解 敏, 夏克文, 石丽莉, 田芸贺, 贺紫平
(河北工业大学电子信息工程学院, 天津 300401)
花朵授粉算法(flower pollination algorithm, FPA)是Yang[1]提出的一种新型元启发式算法,已经被应用到微网的优化调度[2]、雷达探测[3]、视觉跟踪[4]等各个领域,并且效果显著。除了解决单目标优化问题之外,还可以对多目标优化问题进行求解,比如可以将其应用到电力市场的投资组合优化问题中[5]。
近几年来,花朵授粉算法被不断的完善。例如,文献[6]中针对算法的全局寻优能力和收敛速度进行了改进,提出了具有族群机制的FPA算法;文献[7]通过引入量子系统的态叠加特性,利用种群的平均最优位置使种群之间存在等待效应,将改进的算法与基本FPA算法、差分进化(differential evolution, DE)算法和蝙蝠算法(bat algorithm, BA)进行对比,得出改进的算法全局寻优能力更强,收敛速度也有较大提高;文献[8]将FPA算法、社会蜘蛛算法(SSO)应用到图像分割问题,使用类间方差或Kapur方法对解进行评估;而文献[9]将模拟退火算法应用到FPA中,避免了陷入局部最优解以及增强了全局寻优能力,性能优于基本FPA算法。
现如今,由于智能电网和新能源等多领域均取得了巨大发展,使得供配电市场的规模进一步扩大[10],与此同时,电力系统对断路器的要求也越来越严格。所以,改造出性能良好的断路器是必需的。自1960年至今,断路器在小型化、高分断以及低能耗[11]的发展趋向上逐步逼近与完善。目前存在于市场中的断路器,额定电流在2 500~6 300 A范围之内占据很大的比重。面对断路器的能耗问题,如何对能耗模型进行改进一直是社会研究的热点。在国内,杭申电器公司将断路器的能耗优化作为重点[12-13],在国外,西门子等公司在产品的设计阶段把低能耗作为首要考虑的问题。
现主要对花朵授粉算法进行改进以及性能分析,并将改进的算法应用于断路器低能耗优化设计中,希望改进的算法比其他算法性能更好,在断路器能耗优化中得到的能耗值更低。
1 基本花朵授粉算法
基本FPA算法是模拟显花植物授粉现象而提出来的一种元启发式算法,包括异花授粉和自花授粉两个部分,其中异花授粉对应算法空间的全局搜索,自花授粉对应局部搜索[14]。
花朵的授粉过程可以通过4条规则进行描述。
(1)异花授粉是指传粉者在进行交叉授粉时按照莱维飞行机制传播花粉配子时进行的全局授粉过程,表示为


式(2)中:Γ(λ)为标准的伽玛函数;s为步长;s0为最小步长;λ=1.5。
(2)自花授粉可看作是算法整体框架流程中的局部授粉阶段,该规则数学公式为
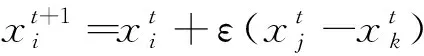
(3)繁衍概率指花的恒常性,繁衍概率的取值大小与对目标问题进行寻优求解的两株花朵之间的近似性成比例关系。
(4)全局授粉和局部授粉之间的转换由转换概率p∈[0,1]控制,受物理上的邻近性、风和水力等不可控因素的影响,在算法的运行中有很重要的作用。
虽然花朵授粉算法引入了莱维飞行机制,能够取得较好的寻优效果,但是该算法还存在容易陷入局部最优解以及收敛速度慢的问题,因此提出一种改进的花朵授粉算法来避免这些问题的发生。
2 改进的花朵授粉算法
2.1 引入鲶鱼效应改进花朵授粉算法
鲶鱼效应是扰动并激活粒子寻优的一种有效手段,原理如图1所示。

图1 鲶鱼效应示意图Fig.1 Schematic diagram of catfish effect
鲶鱼效应起源于挪威人捕鱼的经验,沙丁鱼不爱游动,所以抵港时会大量死亡,但是如果在沙丁鱼池内放一条好动的鲶鱼,沙丁鱼则会感受到威胁,加速游动,避免了其大量死亡的现象。
企业在管理制度中将鲶鱼效应作为一种激励手段,用来鞭策缺乏积极性的“沙丁鱼”,在群智能优化算法中,鲶鱼效应有很多实现的方式,学者们通过对算法后期的目标函数值进行计算,如果函数值没有变化,则可能陷入局部极值,因此可以引入鲶鱼效应,对寻优的花朵加以扰动,进而避免陷入局部最优。
定义鲶鱼个体为:当前适应度值与前一次或者个体历史最优适应度值相同的个体。
除了被标记为“鲶鱼个体”外的所有个体都被称为“沙丁鱼个体”,当沙丁鱼个体受到鲶鱼个体的追赶时,会远离距离自己最近的鲶鱼个体,因此,沙丁鱼个体远离距离自己最近的鲶鱼的距离xaway公式为
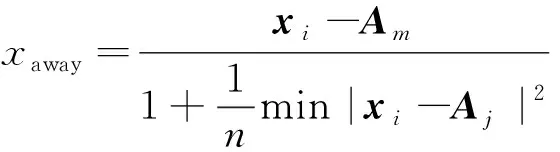
式(4)中:xi为花朵所在位置;Am为距离xi最近的威胁;n为正整数;min|xi-Aj|2表示距离诸多鲶鱼花朵中最小距离的平方,即Aj最终与Am一致。
引入鲶鱼个体对寻优花朵加以扰动从而偏离局部极值,在全局授粉阶段,采用了Levy飞行机制,由于它的较大跳跃以及随机步长,在一定程度上可以避免陷入局部最优解,但是在局部授粉阶段,过程过于平缓,而且缺乏跳动,更容易陷入局部最优,因此,将鲶鱼效应引入局部授粉阶段,其位置更新公式为
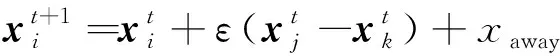
2.2 引入均匀变异算子改进花朵授粉算法
变异来源于遗传算法,主要是指子代的基因按照小概率扰动而产生的变化,常见的变异包括:高斯变异算子、多项式变异算子、均匀变异算子以及大变异算子。其中均匀变异算子可以增加种群的多样性,加快算法收敛速度。
均匀变异算子是指对一个多位置的基因x=(x1,x2,…,xn) 中某一位置上的分量xm∈[a,b],其中1≤m≤n,用[a,b]范围内的服从均匀分布的一个随机数来代替xm,定义为x′m,则x现在变为x=(x1,x2,…,x′m,…,xn),x′m表达式为
x′m=a+r(b-a) (6)
式(6)中:r为[0,1]上的随机数。
由于均匀变异算子的特性,龙军等[15]将粒子群算法应用于配电网重构时,引入了遗传算法中的均匀变异算子,使改进的粒子群算法具有良好的全局搜索能力,并且收敛速度更快。因此为了解决FPA算法收敛速度慢的问题,在算法的全局授粉过程中引入了均匀变异算子,改进后全局授粉更新公式为
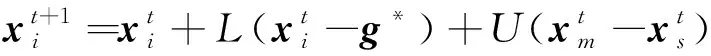
通过引入鲶鱼效应以及均匀变异算子,避免了陷入局部最优解,而且后期收敛速度加快,可以得到改进的花朵授粉算法(catfish effect-homogeneous mutation operator FPA,CEH-FPA),算法步骤如下。
Step 1初始化CEH-FPA算法的各项参数:种群大小规模为N,转换概率为p,流程中最大迭代次数设置为Niter。
Step 2初始化花朵个体的位置,也就是对应解,根据相应位置求解目标函数适应度值,寻找出当前最优的位置和最优目标问题解。
Step 3进入主循环,如果转换概率p>rand(rand为随机数),按照式(7)进行异花授粉,更新下代花朵个体位置,并及时针对越界问题进行处理。
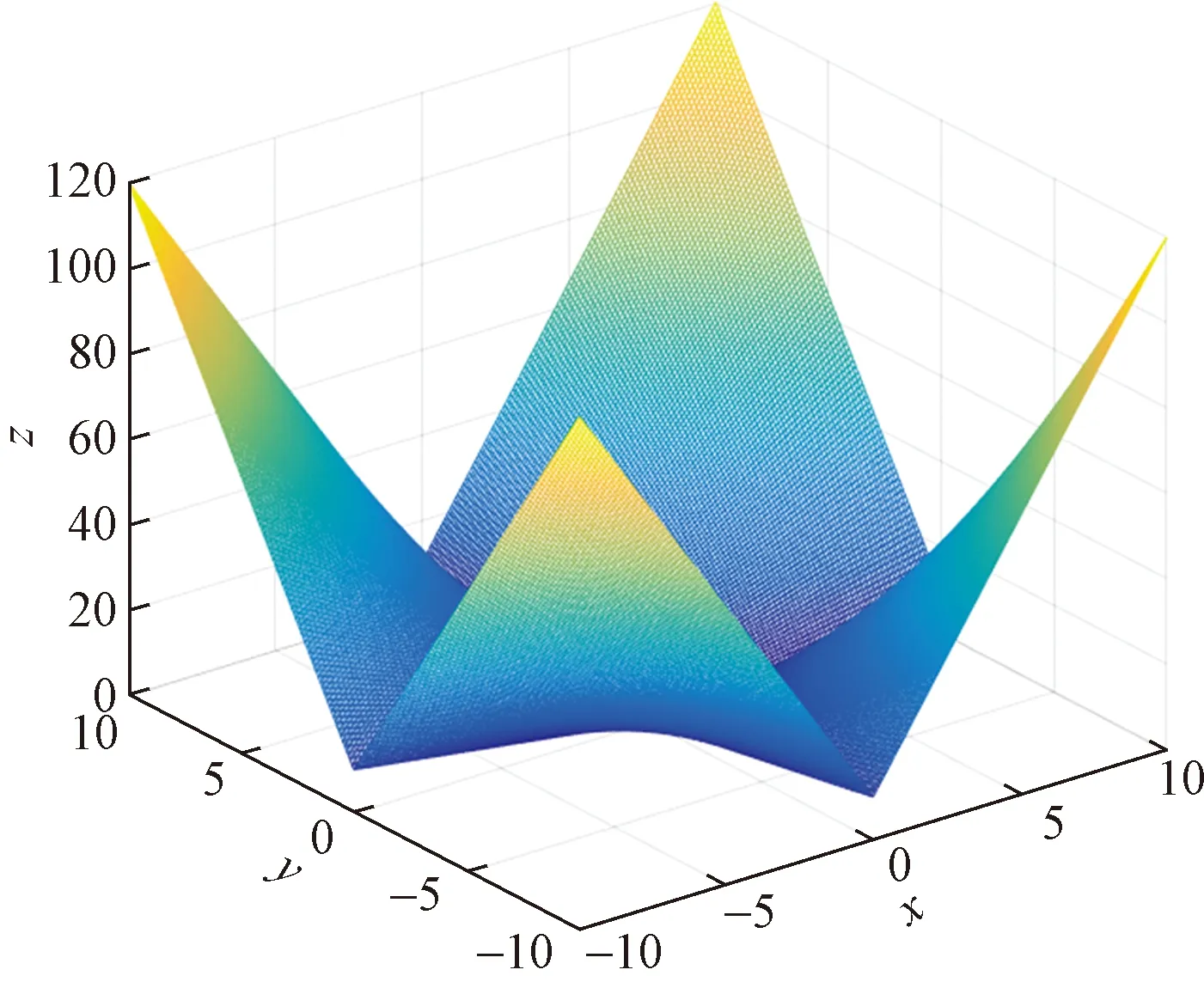
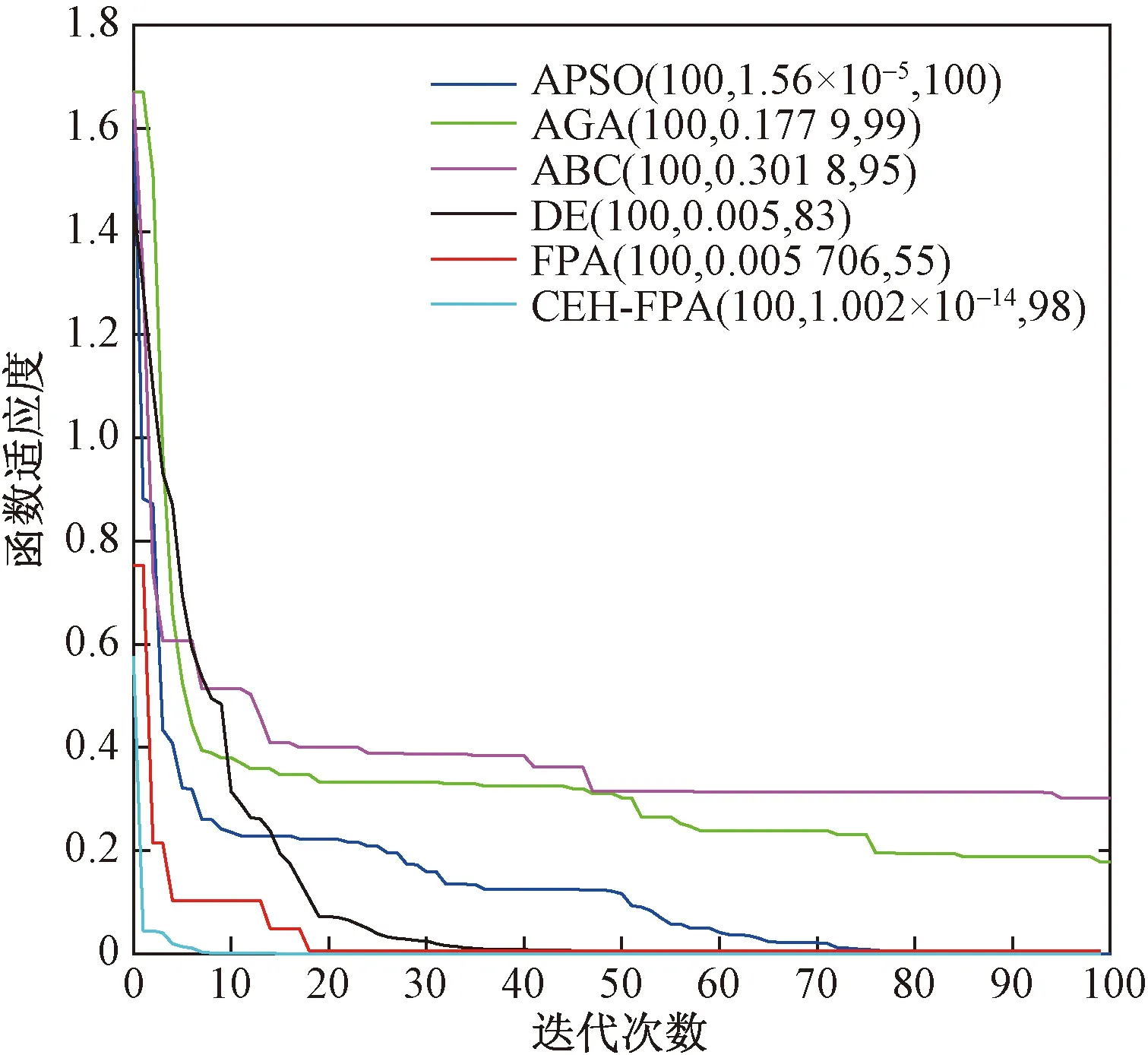
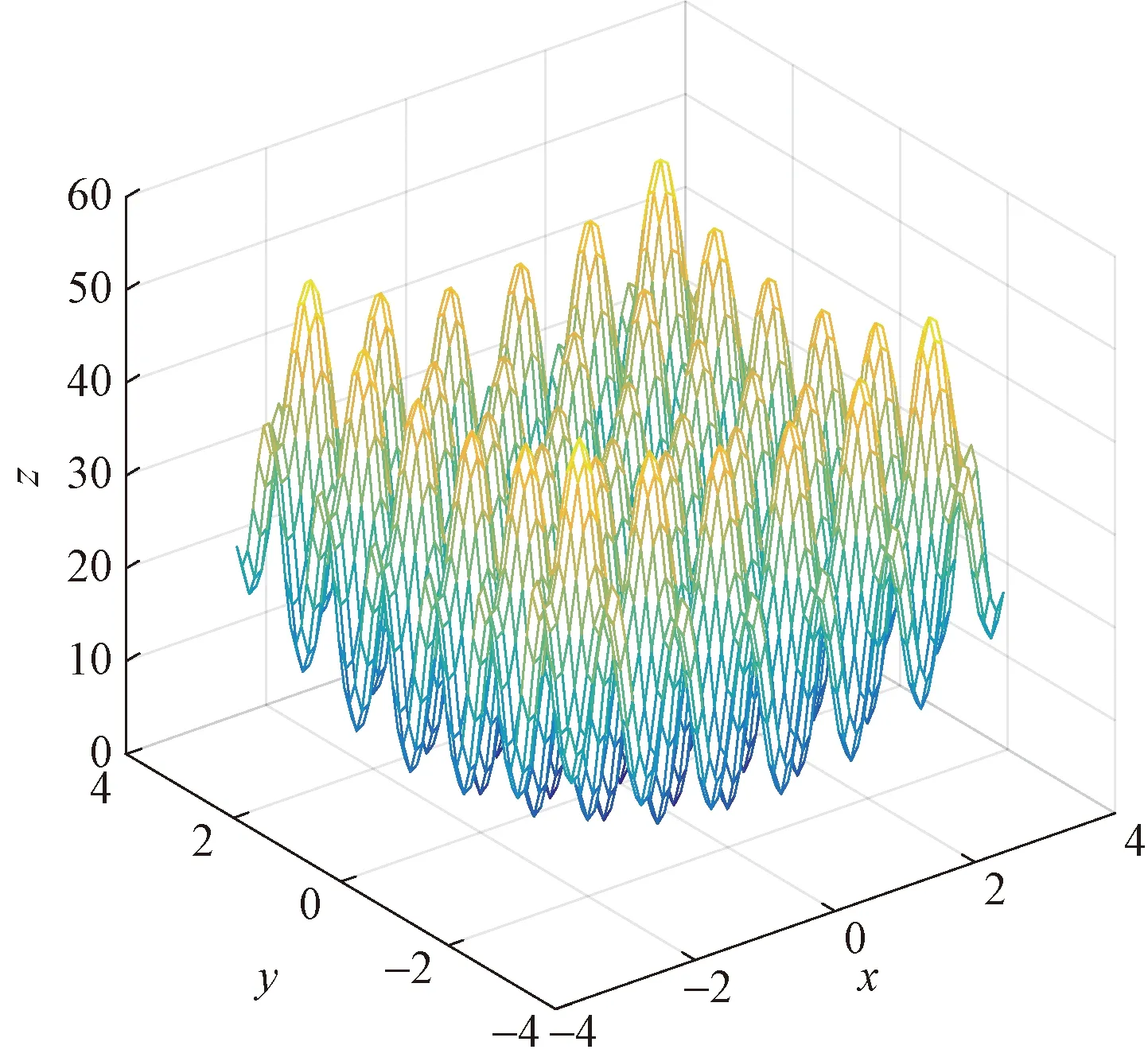
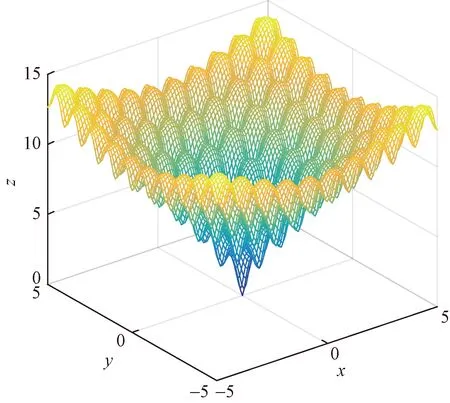
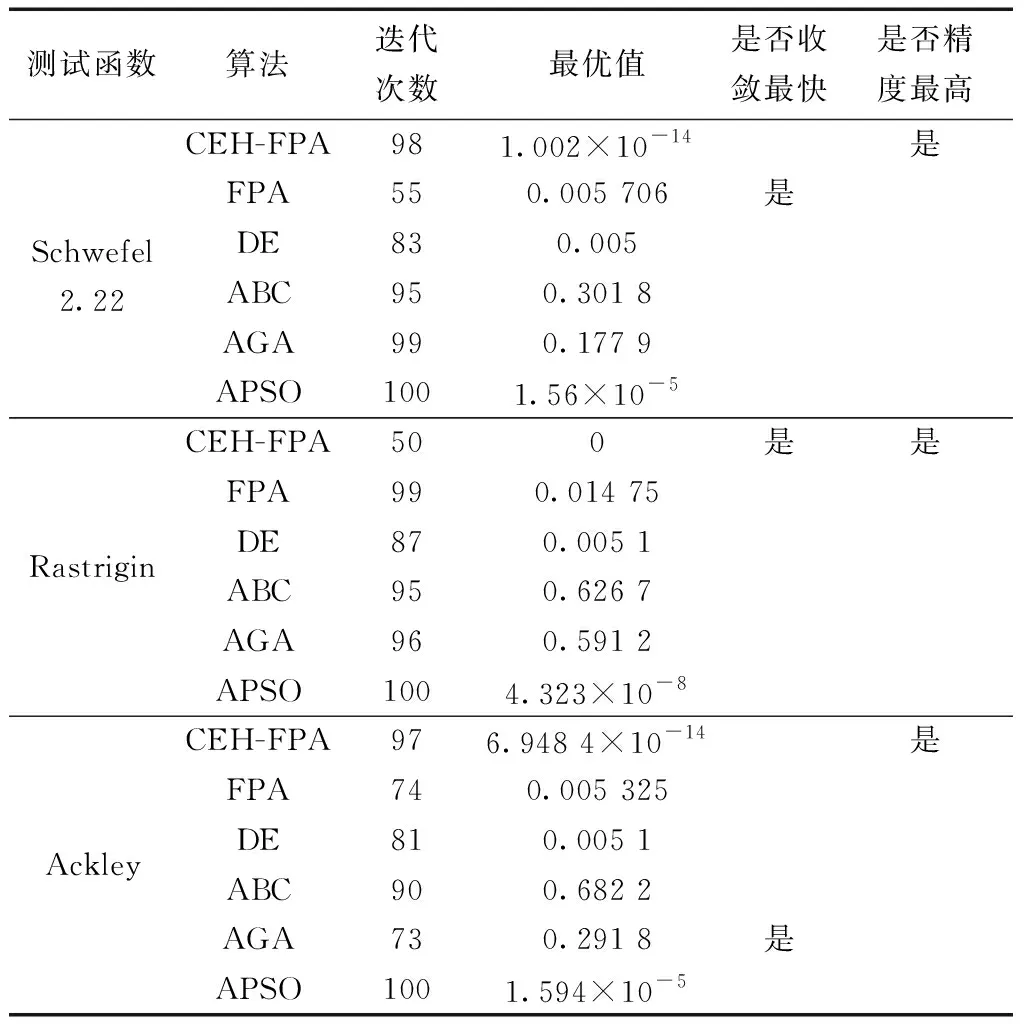
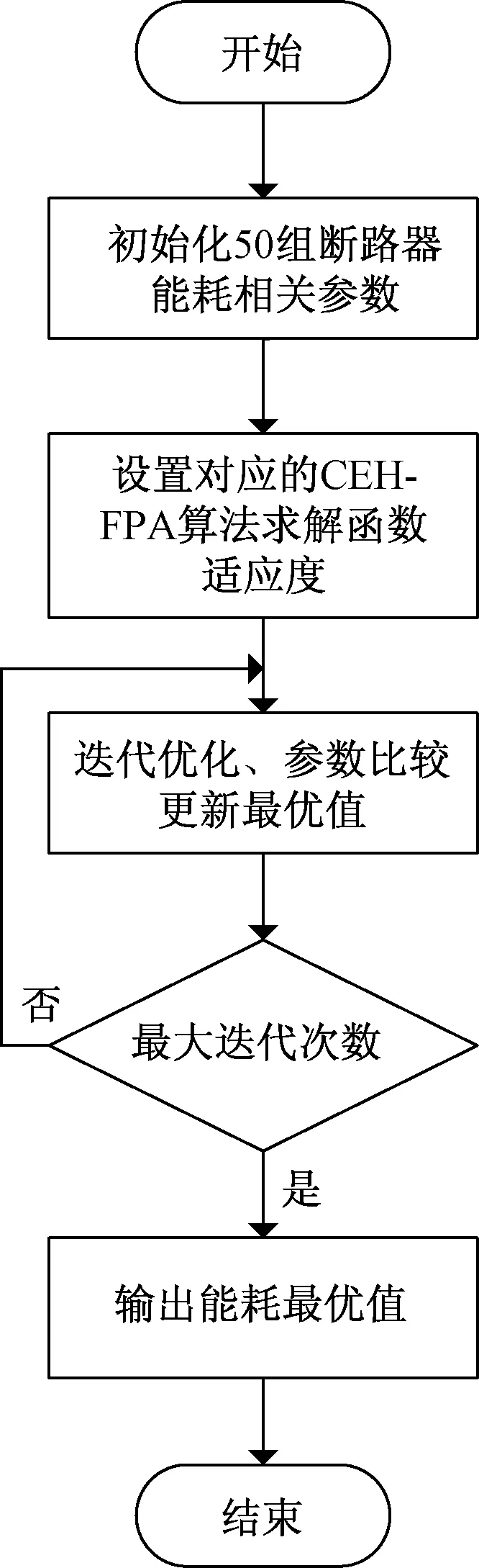
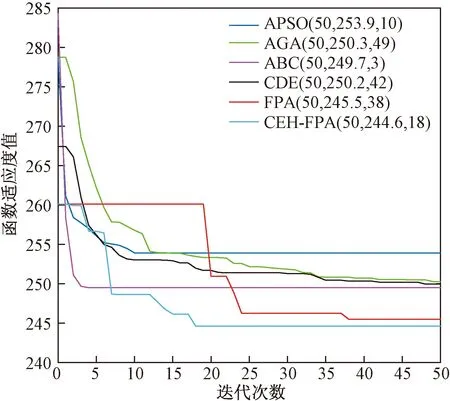
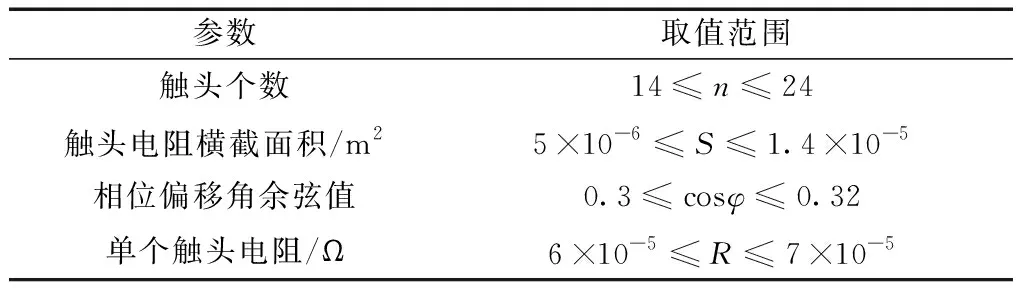
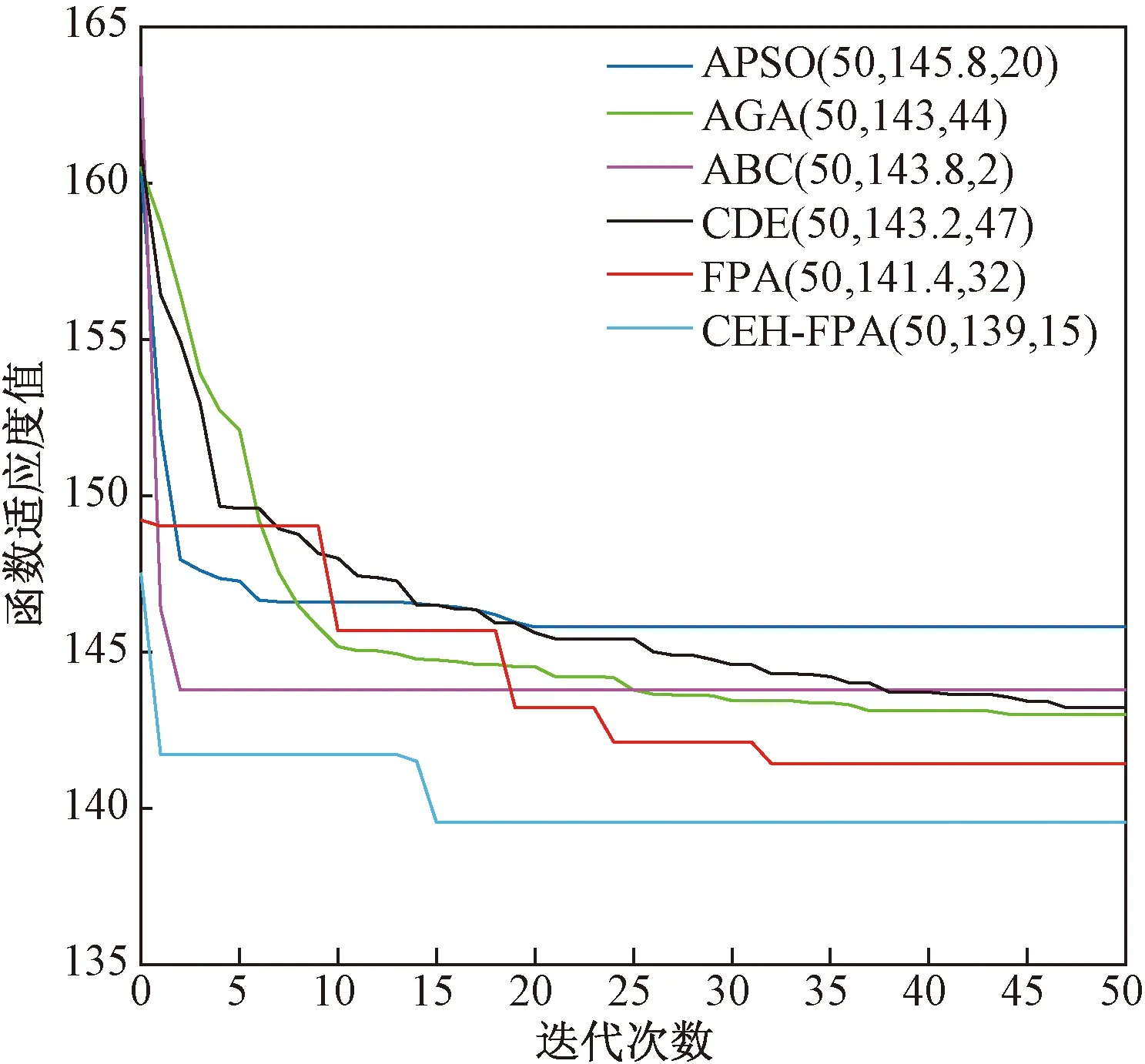
Step 4如果转换概率p Step 5通过Step 3、Step 4计算得出下代解的对应目标函数值,如果该目标函数值精度高,则将下代解和计算得出的下代目标函数值进行相应替换,否则保持当前解和目标函数值大小不变。 Step 6如果下代解计算所得目标函数值精度高于当前代数的全局最优值,更新并记录下代解作为全局最优解位置,下代目标函数优化值作为全局最优值。 Step 7判断算法是否符合结束条件,符合则退出程序并保存记录最优花朵个体位置和全局最优目标函数值,如果不符合则转到Step3,继续循环。 为了验证CEH-FPA算法的性能,本文选取了1个单峰经典测试函数、2个多峰经典测试函数进行测试,并且将CEH-FPA算法与基本FPA算法、差分进化算法(DE)、人工蜂群算法(ABC)、自适应遗传算法(AGA)、自适应粒子群算法(APSO)对比,验证算法性能。 2.3.1 单峰函数 Schwefel2.22函数是一个单峰函数,其三维立体图像如图2所示。 图2 Schwefel2.22函数三维立体图像Fig.2 Three-dimensional stereo image of Schwefel2.22 其表达式如式(8)所示,取值范围为[-10,10],最优适应度值为0。 利用6种算法对测试函数进行迭代寻优,维度D设置为4,种群数量53,重复20次试验,并且求得每次最优值的平均值,可得Schwefel2.22函数寻优迭代仿真图如图3所示。 括号中第一个数据表示迭代次数,第二个表示函数适应度值,第三个表示达到最优解时迭代次数。下同 由图3可知,APSO虽然求解精度高,但是在迭代第100次才取得全局最优解,收敛速度缓慢;AGA算法和基本ABC算法求解精度低;DE算法求解精度和收敛速度在6种算法中处于中间位置;CEH-FPA算法在迭代次数为15时已经达到了精度要求误差在0.01以内,但是仍然继续寻优,并没有陷入局部最优值。 2.3.2 多峰函数 使用多峰测试函数Rastrigin、Ackley进行性能分析。 Rastrigin函数表达式如式(9)所示,取值范围为[-5.12,5.12],最优适应度值为0。 函数三维立体图像、寻优迭代仿真图分别如图4、图5所示。 图4 Rastrigin三维立体图像Fig.4 Three-dimensional stereo image of Rastrigin 图5 Rastrigin函数寻优迭代仿真图Fig.5 Iterative simulation diagram of Rasrtigin function optimization 对于多峰函数Rastrigin,基本ABC算法、AGA算法和APSO算法求解精度低,收敛速度慢;DE算法求解精度较前三种算法较好,但是其收敛速度较慢;CEH-FPA算法不仅求解精度高,而且收敛速度快。 Ackley函数表达式如式(10)所示,取值范围为[-10,10],最优适应度值为0。 函数三维立体图像、寻优迭代仿真图分别如图6、图7所示。 图6 Ackley三维立体图像Fig.6 Three-dimensional stereo image of Ackley 图7 Ackley函数寻优迭代仿真图Fig.7 Iterative simulation diagram of Ackley function optimization 对于多峰函数Ackley,基本ABC算法和APSO算法求解精度低,收敛速度慢,APSO算法收敛速度慢,但是求解精度较高,DE算法求解精度一般,收敛速度慢,而CEH-FPA算法不仅求解精度高,迭代6次时,适应度为0.002 241,已经达到了求解精度,但仍然在一直迭代求解,从而得到了最高求解精度。 为了更加清晰地对算法进行对比,采用表格的形式,对算法进行分析,如表1所示。 通过表1的算法对三个经典测试函数的性能分析可以得出,所提出的CEH-FPA算法较其他算法有更好的开发和开采性能。 表1 测试函数实验结果对比表 电能经过变压器、母排、主电路器、汇流排和支路断路器后,最终到达负载电路,这个过程可能消耗30%~40%的电能,针对断路器能耗高的缺陷,需要合理设计能耗参数,设计出低能耗的断路器[16]。本节主要针对HSW6系列断路器进行分析,其结构如图8所示。 1为断路器进线排;2为桥型触头;3为U形排;4为软联结;5为接触片;6为静触头;7为出线排 断路器内部能耗公式为 式(11)中:P为相级数;In为断路器额定电流;R为电阻;φ为内部回路的相位偏角。 根据式(11),为了降低断路器能耗,可以在结构上使用多组并联的形式,同时考虑电阻体积、回路构造成本以及额外的能量损耗。 (1)考虑电阻体积。 断路器触头电阻计算公式为 R=ρl/S(12) 式(12)中:ρ为电阻率;S为触头电阻横截面积;l为触头电阻的长度。断路器采用回路设计结构,内部有多个触头电阻,可得触头电阻体积为 V=Sl=RS2/ρ=k1RS2(13) 式(13)中:k1为电阻率的倒数。 (2)考虑回路构造成本。 式(13)中,R越小,并联使得器件越大,违背了小型化的原则,体积增大,回路构造成本增大。成本f1与阻值R的关系为 f1=k2/R(14) 式(14)中:k2为回路构造成本系数。 (3)考虑能量损耗。 回路体积增大,触头会产生额外的能量损耗,因此能量损耗f2与阻值R的关系为 f2=k3/R(15) 式(15)中:k3为能量损耗系数。 经过对断路器能耗的分析,以及考虑了电阻体积、回路构造成本、能量损耗等因素的影响,可建立新型断路器能耗数学函数模型为 式(16)中:λ1、λ2为控制系数;n为触头个数;变量为n、S、cosφ、R。当数学函数模型f最小时,同时考虑体积、成本、能耗,此时得到断路器的最低能耗值。 利用改进的CEH-FPA算法对断路器进行优化设计,设计流程图如图9所示。 图9 能耗优化流程图Fig.9 Flow chart of energy consumption optimization 研究断路器能耗值时,参数取值范围不同,断路器的最优能耗值也会发生改变,因此研究两种不同参数取值范围的触头A和B。 3.2.1 触头A 初始化过程中,参数取值范围如表2所示。采用CEH-FPA算法对断路器额定电流为4 000 A的断路器进行优化仿真,结果如图10所示。 表2 触头A参数取值范围Table 2 The parameter range of contact A 图10 A型断路器能耗迭代优化曲线图Fig.10 Energy consumption iterative optimization curve of type A circuit breaker 由图10可知,在优化设计中,CEH-FPA算法所计算出的能耗函数适应度值最低,即求解精度最高,并且收敛速度很快;APSO求解精度不高,收敛速度快,在第10次迭代时得到最优能耗值为253.9 W;AGA算法求解精度低,收敛速度慢,在第49次迭代得到最优能耗值250.3 W;ABC算法在第3次迭代得到最优能耗值249.7 W;DE算法收敛速度慢,在第42次迭代得到最优能耗值250.2 W;CEH-FPA算法求解精度最高,在第18次得到最优能耗值244.6 W。 3.2.2 触头B 初始化过程中,参数取值范围如表3所示。采用CEH-FPA算法对断路器额定电流为4 000 A的断路器进行优化仿真,结果如图11所示。 表3 触头B参数取值范围 图11 B型断路器能耗迭代优化曲线图Fig.11 Energy consumption iterative optimization curve of type B circuit breaker 由图11可知,CEH-FPA算法在迭代15次时达到最优能耗值139 W,较其他算法收敛速度较快,求解精度高。 综上所述,CEH-FPA算法对断路器能耗优化设计效果最好,不仅解决了断路器能耗高的问题,而且性能较其他算法更为优异。 通过利用改进的FPA算法与其他算法进行对比,并对断路器低能耗进行优化研究得出以下结论。 (1)加入鲶鱼效应避免局部最优解,加入均匀变异算子提高后期收敛速度,提出的这种改进算法CEH-FPA 的性能比基本FPA算法、基本ABC算法、DE算法、APSO算法、AGA算法的性能更好。 (2)采用改进的CEH-FPA算法,对断路器的能耗模型进行优化。首先分析断路器的能耗公式,结合影响能耗因素进行数学建模,然后再将算法应用到优化设计中。试验结果表明,CEH-FPA算法大大提高了设计的效率和精度,实现了断路器低能耗性能的设计目的。 CEH-FPA算法不仅可以用于断路器的优化设计中,也可以将设计方法和思路推广到其他的工程模拟优化计算中,从而更好地取代传统的靠经验估算和大量样机制作的方法。2.3 测试函数
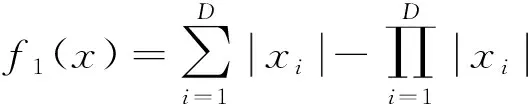


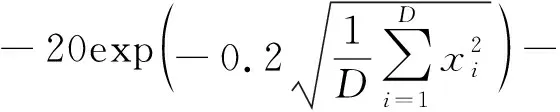
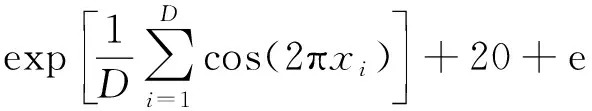

3 断路器能耗及参数优化仿真
3.1 断路器模型
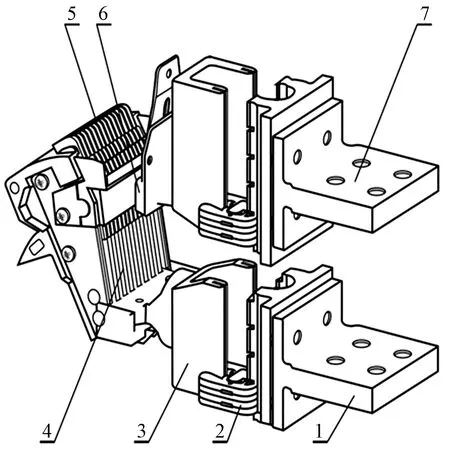
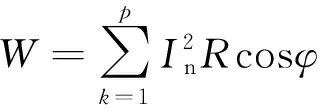
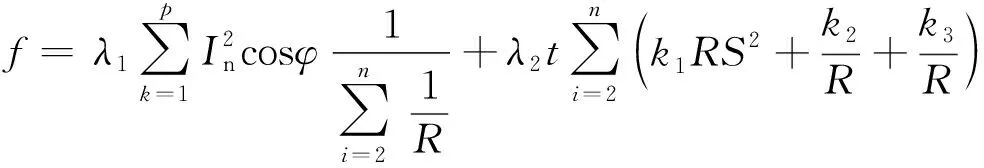
3.2 断路器优化设计

4 结论
