基于天气聚类的光伏电站辐照度预测

张 玉, 王瑜琳

(1.桂林理工大学机械与控制工程学院， 桂林 541004； 2.广西建筑新能源与节能重点实验室， 桂林 541004)

目前光伏产业发展速度较快，新增装机容量不断增加，其在能源策略中的重要地位在国际上已得到普遍认可。由于光伏发电受外界环境影响较大，其输出功率具有较强的随机性以及波动性，并网时容易影响电力系统的安全稳定运行，降低电能质量，且不利于电力系统的调度以及规划，因此对光伏电站发电量进行预测极有必要。太阳辐照度是影响光伏输出功率最显著的因素，对其进行精确预测有助于提高光伏输出功率的预测精度，具有非常重要的意义。

目前太阳辐照度预测主要基于太阳辐射传递物理模型、卫星图像技术以及大数据驱动技术等，其中太阳辐射传递物理模型可以直接对太阳辐照度进行预测，不依赖任何历史数据，主要预测模型有美国采暖、制冷与空调工程师协会(American society of heating refrigerating and air-conditioning engineers，ASHRAE)推荐的ASHRAE模型、太阳辐射(hotel solar radiation，Hottel)模型、神经网络估算太阳辐射(artificial neural network estimating solar radiation，ESRA)模型等[1-4]，其建模过程较为复杂，且难以模拟极端异常天气情况。卫星图像技术则需要通过昂贵的专业设备收集数据，且受测量设备的精度以及测量方法的影响较大，其预测精度一般不高。大数据驱动技术主要依赖历史数据，从大量数据中挖掘其内在规律，建立历史辐照度与未来辐照度之间的映射关系，该模型结构简单、计算效率较高，是目前太阳辐照度预测的主要方法。然而，大数据驱动技术仅仅通过历史辐照度数据建模，难以反映气象因素与辐照度之间的非线性关系，其预测精度有限。

基于辐照度的天文学模型结合天气类型进行辐照度预测，通过建立太阳光照与地球大气层的几何模型，求解地外辐照度计算公式并修正晴天透明度系数，然后依据天气类型与历史辐照度进行聚类分析，计算相应的权重系数，建立基于天气聚类的太阳辐照度预测模型。通过桂林理工大学分布式光伏发电站实测数据验证，与传统的晴天模型、递推最小二乘法 (recursive least square，RLS)模型、小波变换(wavelet transform,WT)模型相比，验证天气聚类模型的适应性和准确率。

1 辐照度模型建立

1.1 太阳光照射与地球坐标关系

在引入太阳辐照度前，先建立太阳与地球的坐标关系，其几何模型如图1所示[5-8]。

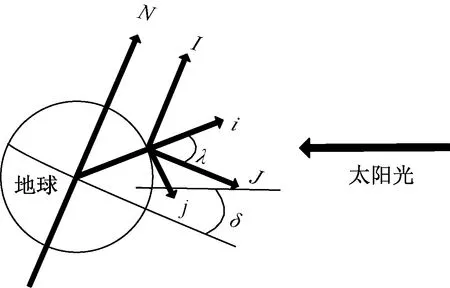
I、J坐标系分别指向正北方、赤道平行方向，称为时角坐标系；i、j坐标系分别指向太阳垂直点、地平线，称为地平坐标系

时角坐标系和地平坐标系之间关系式为

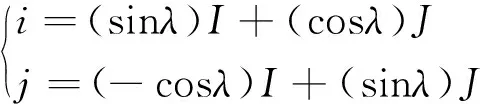
式(1)中：λ为测量点的纬度。正午时分时进行几何模型分析，以地平坐标系为参考坐标时，指向太阳的单位矢量可以写为

s=(cosz)i+(sinzcosaz)j-(sinzsinaz)k(2)

式(2)中：z为天顶角；az为太阳方位角。

以时角坐标系为参考坐标时，指向太阳的单位矢量可以写为

s=(cosδ)I+(sinδcosω)J-(sinδcosω)K(3)

式(3)中：δ为赤纬角；ω为太阳时角。

由于地平坐标系与时角坐标系中的矢量s相同，联立式(1)～ 式(3)，可得

cosz=sinδsinλ+cosδcosλcosω(4)

sinzcosaz=cosδcosωsinλ-cosλsinδ(5)

sinzsinaz=cosδsinω(6)

一年中的天数是确定的，根据Cooper公式可计算出太阳的赤纬角δ,即

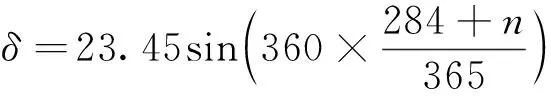
式(7)中：n为一年中的第几天的天数；一年中赤纬角δ的变化范围为-23.45°～23.45°。

由式(4)～ 式(7)可知，当观测点的地理纬度确定时，当天的时间变化可通过太阳时角进行表示，日出或日落时分，太阳天顶正好等于π/2，此时cosz=cos90°=0，太阳处于地平线上，则有

cosω=-tanδtanλ(8)

天顶角的余弦函数反映了太阳的辐照强度投射到地平表面上的光照比，结合式(4)～ 式(8)，可以建立地表辐照度Eb与太阳时角ω、赤纬角δ、地理纬度λ的比例关系，即

Eb∝(sinδsinλ+cosδcosλcosω) (9)

1.2 地外辐照度

大气层外的太阳辐照强度仅仅与日期的周期变化有关，在误差允许范围之内，根据太阳方位角与时角之间存在的关系，可推导地外辐照度计算公式[9]为

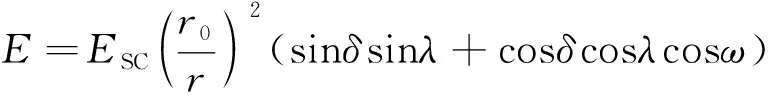
式(10)中：E为地外辐照度；ESC为太阳常数(1 367 W/m2)；(r0/r)2为日地距离修正系数，其计算公式为

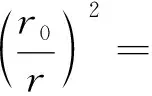
0.000 086sin(2θ)-0.008 349cosθ+

0.000 115cos(2θ) (11)

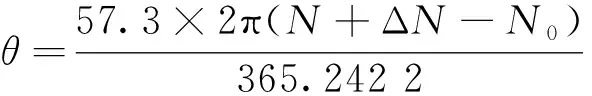
N0=79.676 4+0.244 2(Y-1 985)-

INT[0.25(Y-1 985)] (13)

式中：θ为日角；N为积日；ΔN为积日的修正值；Y为年份。

对式(10)中的太阳时角ω进一步简化，可得

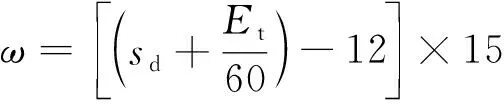
ET=0.002 8-1.985 7sinθ+9.905 9sin(2θ)-7.092 4cosθ-0.688 2cos(2θ) (16)

式中：Sd为当地地方时；ET为时差；ST为地方标准时的小时数；F为地方标准时的分钟数；γ为测量点的经度。

通过测量地的经、纬度以及时间，可推导出该地任意时刻对应的地外辐照度理论值。以桂林(经度110.300°，纬度25.333°)为例，2015年7月20日13：00的太阳地外辐照度功率为1 315.3 W/m2。

1.3 直射和散射透明度系数

太阳辐射从地外穿过大气层到达地表，其传播受大气量的影响较大，会产生一定的衰减，因此对地表辐照度进行计算时，需要考虑大气层的衰减系数。根据Kretith和Kreider提出的经验公式[10]可得直接辐射透明度系数τb，即

τb=0.56(e-0.56Mh+e-0.095Mh) (17)

式(17)中：Mh为一定地形高度下的大气质量，其表达式如下：

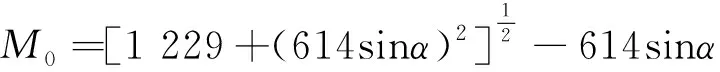
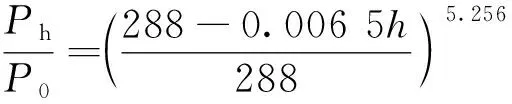
式(20)中：M0为海平面上的大气量；α为太阳高度角；Ph/P0为大气层修正系数；h为海拔高度。

散射辐射τd与直接辐射τb之间存在线性关系，可以通过公式(21)表示：

τd=0.271-0.294τb(21)

故太阳直射辐照度为Eb=Eτb；散射值为Ed=Eτd；地表总辐照度为Et=Eb+Ed。根据式(10)～ 式(21)，可以求出不同太阳高度角时对应的透明度系数，进而预测晴天条件下太阳辐照强度。

1.4 透明度系数的优化

由式(17)～ 式(21)可知，透明度系数是建立在经验系数基础之上，在进行辐照度预测时需要对透明度系数进一步优化。利用桂林理工大学分布式并网光伏发电站，在晴天气候条件下，根据地表辐照度测量值与地外辐照度理论值，求出平均实际透明度系数序列，根据经验公式求解透明度系数，用MATLAB进行对比分析如图2所示。

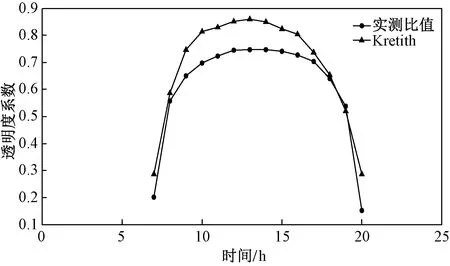
图2 理论曲线与实际值曲线Fig.2 Theoretical curve and the actual value of the curve

进行实际数据计算分析时，对一些存在异常的数据进行以下修正：①去除异常值，如辐照度为负值或大于地外辐照度理论值的数据；②若有数据遗失，则采用线性插值法进行数据拟合与补全。

从图2可以看出，采用经验公式计算的透明度系数与实际数据计算的值总体趋势相同。在数值上，经验计算值比实际值高15%左右，对上述两条曲线进行拟合分析，公式为

τt=0.000 1x6-0.004x5+0.005 4x4-

0.079 3x3+0.577 3x2-1.678x+1.359 (22)

故采用经验公式计算时，需要乘以比例系数τt，则地表辐照度修正公式为

E′=τtEt=0.85(Eb+Ed) (23)

1.5 光伏阵列辐照度

为了使光伏阵列全年接收到的太阳辐照度最大化，在实际应用中安装光伏阵列时需要倾斜一定的角度，对地表总辐照度公式进一步推导，可得出太阳光照与倾斜阵列之间空间坐标关系的几何模型[11]如图3所示。

图3 太阳光与光伏阵列坐标系关系Fig.3 The coordinate relationship between the sunlight and PV array

图3中，i、j、k表示光伏阵列空间坐标系的三维参考方向；n表示光伏阵列倾斜面的单位矢量；γ表示方位角；β表示光伏阵列的倾斜角；s表示指向太阳的单位矢量，则各变量之间的关系式可表示为

n=(cosβ)i+(sinβ)(cosγ)j-(sinβ)(sinγ)k(24)

对于固定光伏阵列，其方位角一般选取正南方，即γ=0，则式(24)可进一步简化为

n=(cosβ)i+(sinβ)j(25)

联立式(4)、式(5)、式(25)，可以推导出光伏阵列斜角β与太阳水平辐照度之间的关系为

cos(n,s)=coszcosβ+sinzcosαzsinβ=

sinδsin(λ-β)+cosδcos(λ-

β)cosω(26)

由式(17)～式(26)可推导出光伏阵列倾斜角为β时对应的太阳辐照度。

1.6 天气聚类

根据式(4)～ 式(26)，可计算出理想条件下地表总的辐照度，而透明度系数常受到云层厚度、水蒸气、大气颗粒物的影响，会产生不同的透明度系数，利用上述公式计算辐照度时预测结果精度较低。不同的天气类型会影响大气层结构，故引入天气类型与透明度系数之间的关系，进而提高上述公式的计算精度。

晴天条件时，大气层物理结构相对稳定，透明度系数也相对固定，根据Kretith和Kreider理论，由式(17)来计算出透明度系数。在其他天气类型下，根据历史辐照度进行聚类，由不同天气类型的衰减系数与地表辐照度相结合，计算出新的比例因子，进而提高太阳辐照度的预测精度。

2 辐照度的预测

2.1 天气类型与辐照度的聚类

大气物理结构比较复杂，产生的天气类型也多种多样，在进行聚类分析前，需要对天气类型进行分类。气象部门定义有33种天气类型，如果对光伏阵列接收的辐照度按这些种类去聚类，在进行辐照度预测时会产生两方面的问题：一是天气类型种类繁多，需要大量数据样本；二是有些天气类型出现的概率很小，此条件下的历史辐照度数据记录较小，难以建模分析。所以，先将气象部门划分的天气类型进行分类，分为晴天、阴天、小雨、大雨4种典型天气类型。这4种天气类型所对应的地表辐照度与地外辐照度变化规律如图4所示。

由图4(a)可看出，晴天时，地表与地外辐照度曲线变化规律较为相似，曲线相关性较强。由图4(b)可看出，多云时，地表辐照度受云层的影响波动较大，地表与地外辐照度曲线形状基本相似。由图4(c)可看出，小雨时，地表辐照度衰减较大，曲线波动频繁，与地外辐照度相差较大。由图4(d)可看出，大雨时，地表辐照度很小，且与地外辐照度基本不相关。

图4 地表与地外辐照度曲线Fig.4 Surface and ground radiation curve

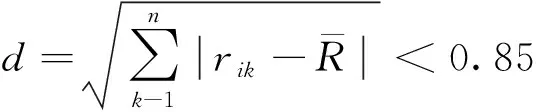
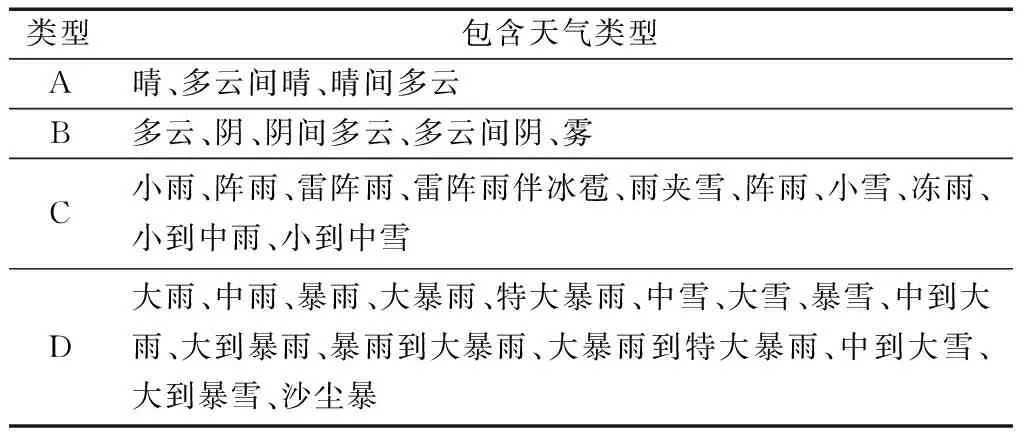
表1 天气类型

2.2 各种天气类型下的预测

根据式(23)可以准确预测A类天气的辐照度，

但对于B、C、D等天气类型时其预测精度不高，所以需要对4种天气类型相对应的辐照度进行分析，找出相互对应关系。利用桂林理工大学气象站记录该校分布式发电站的近几年辐照度的逐时数据，对4种天气类型的辐照度进行对比分析，如图5所示，使用MATLAB工具箱进行多项式曲线拟合，并对拟合曲线进行积分，分析各条曲线之间的相互对应的关系。

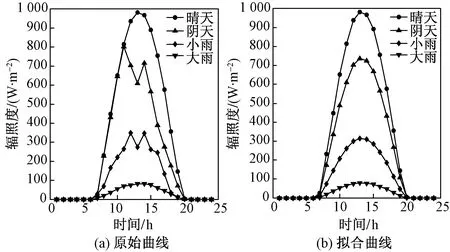
图5 各类天气类型辐照度曲线Fig.5 Weather type of radiation curve

各天气类型下的拟合公式为

ES=628.8x6-266.8x5+45.79x4-3.464x3+0.118x2-0.001 5x-400.8 (27)

EC=417.6x6-200.1x5+34.34x4-2.598x3+0.089x2-0.001 1x-330.6 (28)

EL=201.2x6-85.4x5+14.65x4-1.108x3+0.038x2-0.000 4x-141.1 (29)

EH=50.31x6-21.35x5+3.663x4-0.277x3+0.009x2-0.000 12x-35.26 (30)

式中：ES、EC、EL、EH分别为晴天、阴天、小雨、大雨天气类型的辐照度。

由图5(a)可知，各类曲线之间没有明显的线性关系，图5(b)在进行拟合后，以晴天曲线为参考点，其他三类天气类型曲线均存在一定的衰减比例关系。定义各天气类型与晴天类型之间的衰减系数为φ，经过计算，对于A类型中多云间晴、晴间多云两种天气类型的衰减值为0.9，B、C、D天气类型分别对应的衰减值为0.74、0.23、0.09。所以，基于各种天气类型辐照度预测修正公式为

ET=φE′t=φτtEt=0.85φ(Es+Ed) (31)

3 实验仿真分析

仿真数据来自桂林理工大学分布式光伏发电站，如图6所示，该建筑曾参加了2013年国际太阳能十项全能竞赛。气象数据来源于同地点的自动气象站所采集的实时数据，如图7所示。

图6 桂林理工大学分布式光伏发电站Fig.6 Distributed photovoltaic power station of Guilin University of Technology

图7 桂林理工大学气象站Fig.7 Meteorological station of Guilin University of Technology

该系统的额定输出功率为11 kW，日最大发电量可达50 kW·h，系统具有实时采集功能，可以对光伏发电量、天气状况和气候特征等数据实时记录。实验数据来源于该分布式发电站2015年7月1日—31日的记录，每天7:00—20:00隔15 min采集一次，共采集到1 643个点的地表辐照度样本数据，用后318个数据对模型进行测试。同时为了更好地评估预测效果，与晴天模型、RLS模型等两种常用预测模型进行对比分析，三种预测算法对辐照度的预测结果如图8所示，绝对误差如图9所示，综合评价如表2所示。

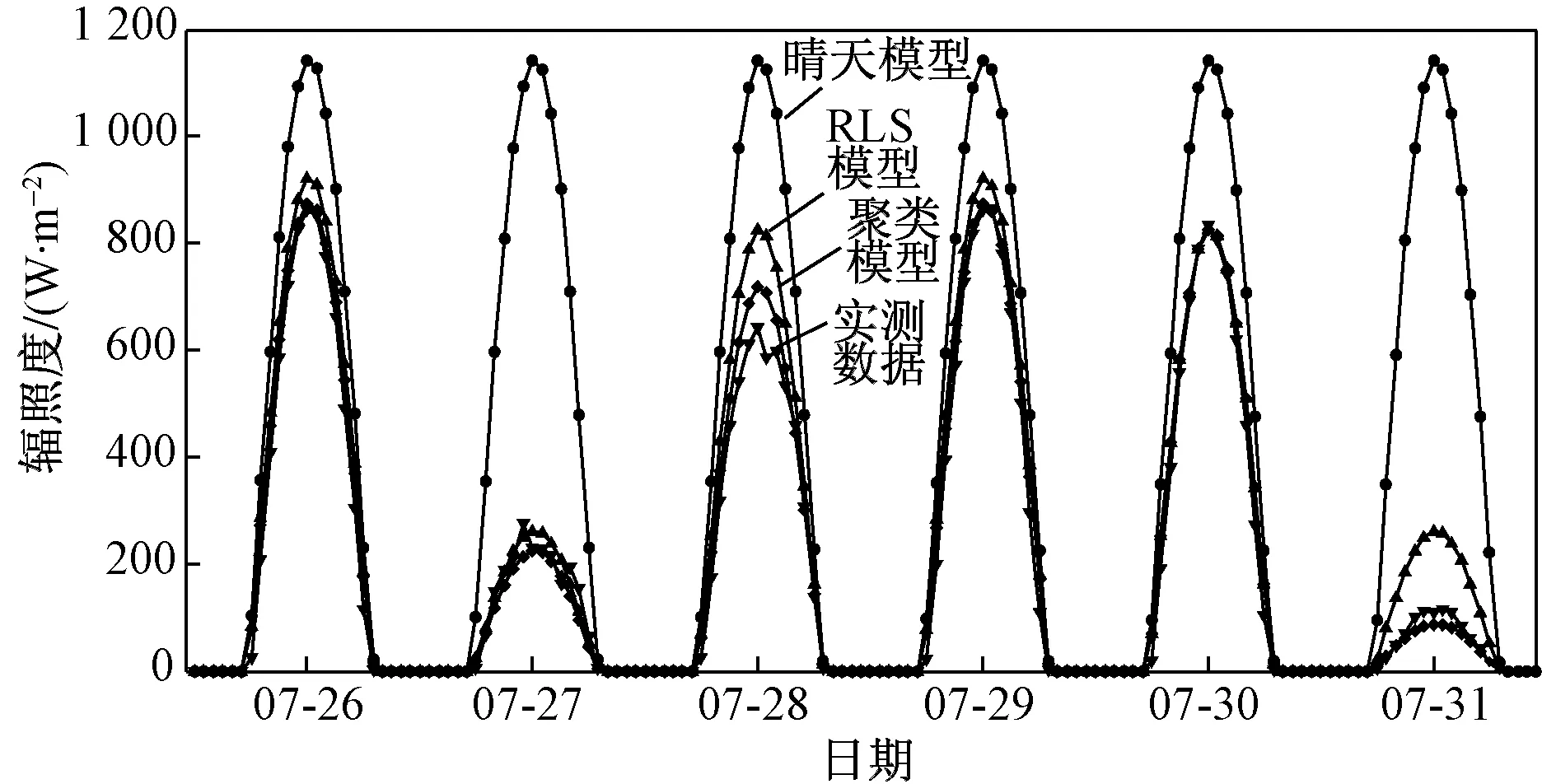
图8 晴天、RLS、聚类预测结果与实际值比较图Fig.8 The comparison of sunny,RLS, Cluster model and actual value

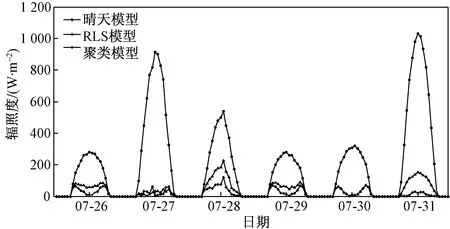
图9 晴天、RLS、聚类绝对误差曲线图Fig.9 The prediction error comparion of sunny,RLS and cluster

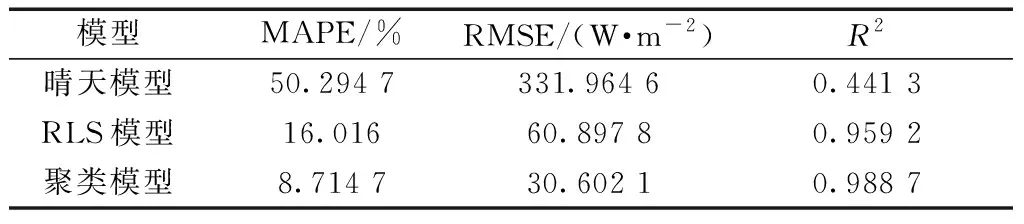
表2 预测结果综合评价表

由图8可看出，天气聚类模型预测结果比晴天模型、RLS模型预测结果更接近于实际曲线，表明天气聚类模型预测精度更高。由图9绝对误差曲线图可看出，天气聚类模型的绝对误差曲线相对于其他两种模型曲线的波动性要小很多，即天气聚类预测模型比其他两种预测模型更加稳定。

通过表2可以看出，对未来几天辐照度进行连续预测，天气聚类模型准确度相对较高，说明预测模型与天气类型相结合的合理性。晴天模型和RLS模型的RMSE分别为331.964 6、60.897 8 W/m2，聚类模型RMSE减小至30.602 1 W/m2；MAPE也分别由50.294 7%、16.016 0%降至8.714 7%；相关性也由0.441 3、0.959 2增加至0.988 7；所以，相对于晴天模型和RLS模型，天气聚类模型的平均相对误差及均方根误差都最小，表明天气聚类预测模型预测效果最好，预测精度相对于其他两种预测模型要好。

基于天气聚类预测模型结合多种天气类型，对A、B、C、D类型的历史天气进行逐时辐照度预测。晴天模型、RLS模型和天气聚类模型预测前后的误差指标，以及预测结果误差对比如表3所示。

表3 预测结果误差比较

由表3结合图9可看出，对于A、B、C三类天气类型，辐照度表现出一定的变化规律性，验证了引入天气聚类的必要性。在A、B、C三类天气类型下，已有的晴天预测模型的RMSE分别为105.383 6、254.960 2、448.105 2 W/m2，RLS预测模型的RMSE分别为77.035 0、109.720 2、35.961 5 W/m2，而基于天气聚类预测模型的RMSE分别降至31.221 2、82.274 5、31.383 5 W/m2；晴天预测模型的MAPE分别是19.1794%、42.0168%、75.4047%，RLS预测模型分别是14.925 7%、23.750 2%、23.542 6%，天气聚类预测模型则减少到5.573 5%、20.072 9%、16.290 0%；对于D类天气类型，前两类预测模型准确度不高，而天气聚类预测模型准确率相对较高。

由表3还可以看出，对于A类型天气，三种预测模型相关性都较高。晴天预测模型在B、C、D三类天气下相关性逐渐降低，甚至出现负相关。RLS预测模型在B、C三类天气下相关性保持在 0.883 7 以上，而天气聚类预测模型相关性至少在0.913 7以上。而D类型天气，晴天预测模型与RLS预测模型相关性都极低，表明D类天气辐射度变化规律性不强，预测比较困难。天气聚类预测模型能够保持较强的相关性，说明天气聚类预测模型能适应各类型天气下的辐照度预测，具有一定的可行性。

在进行天气聚类及模型参数修正时，可以根据不同历史数据及天气类型的复杂性进行调整，修正权值由历史数据计算得出，在进行异常的数据处理时，能够保证修正后的参考值与预测日天气类型是相同的。划分天气类型时进一步考虑相同天气类型下的地表辐照度衰减的差异，通过透明度系数进行调整，从而计算出较合适的权重系数。

从三种模型的预测结果、误差以及相关性系数分析可知，天气聚类模型的拟合优越度要比晴天、RLS模型高，预测准确率更高。

4 结论

基于辐照度的天文学模型结合天气类型进行辐照度预测，通过建立太阳光照与地球大气层的几何模型，求解地外辐照度计算公式并修正晴天透明度系数，然后依据天气类型与历史辐照度进行聚类分析，计算相应的权重系数，建立基于天气聚类的太阳辐照度预测模型。通过桂林理工大学分布式光伏发电站实测数据验证，基于天气聚类预测模型在A、B、C、D四种天气类型下的RMSE分别最小修正45.813 8、27.445 7、4.578 0、94.186 3 W/m2；MAPE分别最小修正9.352 2%、3.677 3%、7.252 6%、64.094 1%；相关性系数分别至少提高0.026 5、0.030 0、0.056 0、0.894 3，与传统的晴天模型、RLS模型相比，天气聚类模型具有更强的适应性、更高的准确率。