中浅埋深矩形巷道顶板围岩弹塑性变形

谷拴成， 王 盼， 杨超凡

(西安科技大学建筑与土木工程学院， 西安 710054)

煤炭作为中国的主要能源支柱，对国家经济起着举足轻重的作用[1]。随着采煤机械化程度提高，煤矿开采强度进一步加大，开挖过程中由于顶板变形破坏而引发的事故越来越严重。因此对巷道顶板围岩变形的研究显得尤为重要。现阶段，对于圆形巷道围岩变形分析已有成熟理论[2-4]，谷拴成等[5]基于锚杆加固效应，建立巷道计算模型并进行弹塑性分析，导出了圆形巷道围岩应力、位移解析解。林志斌等[6]采用离散颗粒元软件分析了5种侧压力系数下圆形巷道周边岩体的应力差、位移等，得到了圆形巷道周边岩体应力、变形的变化规律。以上研究促进了圆形巷道理论研究的发展。在实际工程中，矩形巷道因其施工相对简单，有利于采煤工作面端头支护及回采工作面的快速推进等优点，在中国煤矿开采中广泛应用[7]。对于矩形巷道顶板变形研究主要通过数值模拟、现场监测以及模型试验的方法进行[8-10]，因此有必要对矩形巷道顶板围岩变形展开理论研究。

现依据现有理论，建立矩形巷道顶板梁模型，考虑煤岩体抗压强度大于抗拉强度的特点，根据弹塑性理论，研究巷道顶板在上覆煤岩体自重应力场作用下的挠曲变形。为了验证理论的可靠性，进一步依据神木市柠条塔煤矿的现场生产资料，结合数值模拟对规律进行验证。最后，通过对柠条塔煤矿s12001运输巷道顶板围岩变形进行监测，将现场实测结果与理论计算值以及数值模拟的结果进行对比分析，对本文理论的现场适用性进行验证。

1 矩形巷道顶板梁模型建立及分析

1.1 顶板梁模型建立

根据巷道顶板围岩变形规律，可将巷道顶板简化为简支梁，顶板梁材料视为理想弹塑性材料，按平面应变问题进行分析。因为要求得顶板表面处的下沉值，故以顶板表面位置为梁的中性层(围岩的弹性模量可适度降低)，取顶板梁计算长度为2l，变梁高为2h、2h′，梁宽度为b，梁仅承担上覆岩土体自重荷载q，建立如图1所示模型。

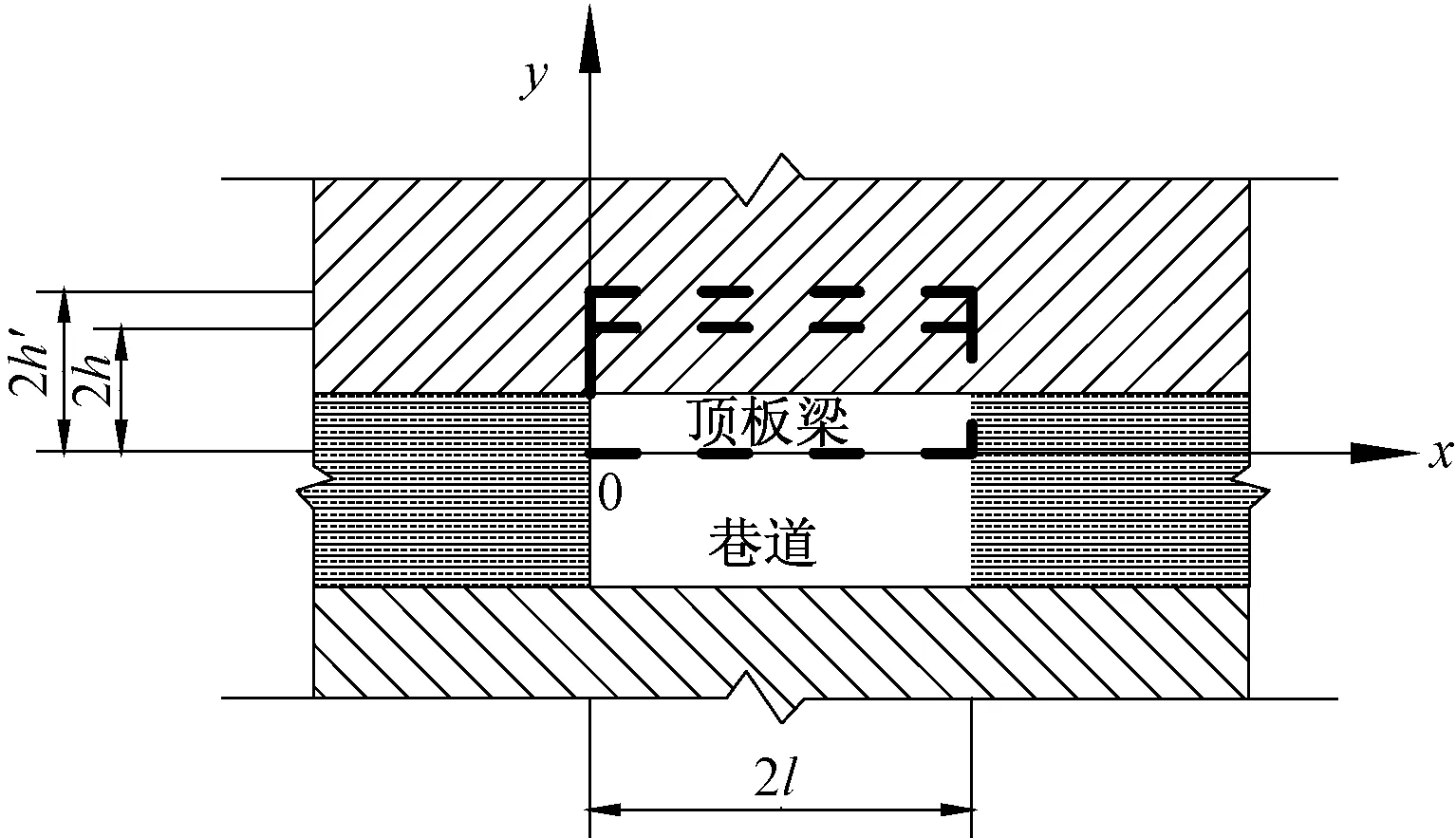
图1 顶板梁模型Fig.1 Roof beam model

1.2 顶板梁弹性状态分析

顶板梁整个截面处于弹性状态时，顶板梁跨中弹性弯矩Me[11]为

(1)

以顶板梁截面上的最大正应力不超过顶板围岩的极限抗拉强度为条件，可以得到顶板围岩处于弹性极限时梁高与围岩极限抗拉强度的关系，即

(2)

式(2)中：y′为计算点距中性轴的距离，m；I为惯性矩,m4；σt为顶板围岩极限抗拉强度,MPa；σmax为顶板围岩所受的最大正应力,MPa；he为顶板围岩处于弹性极限状态时的梁高,m。

根据式(2)可得到处于弹性极限状态下的梁高为

(3)

弹性状态下顶板梁跨中挠度方程ωe[11]为

(4)

式(4)中：E为弹性模量,MPa。

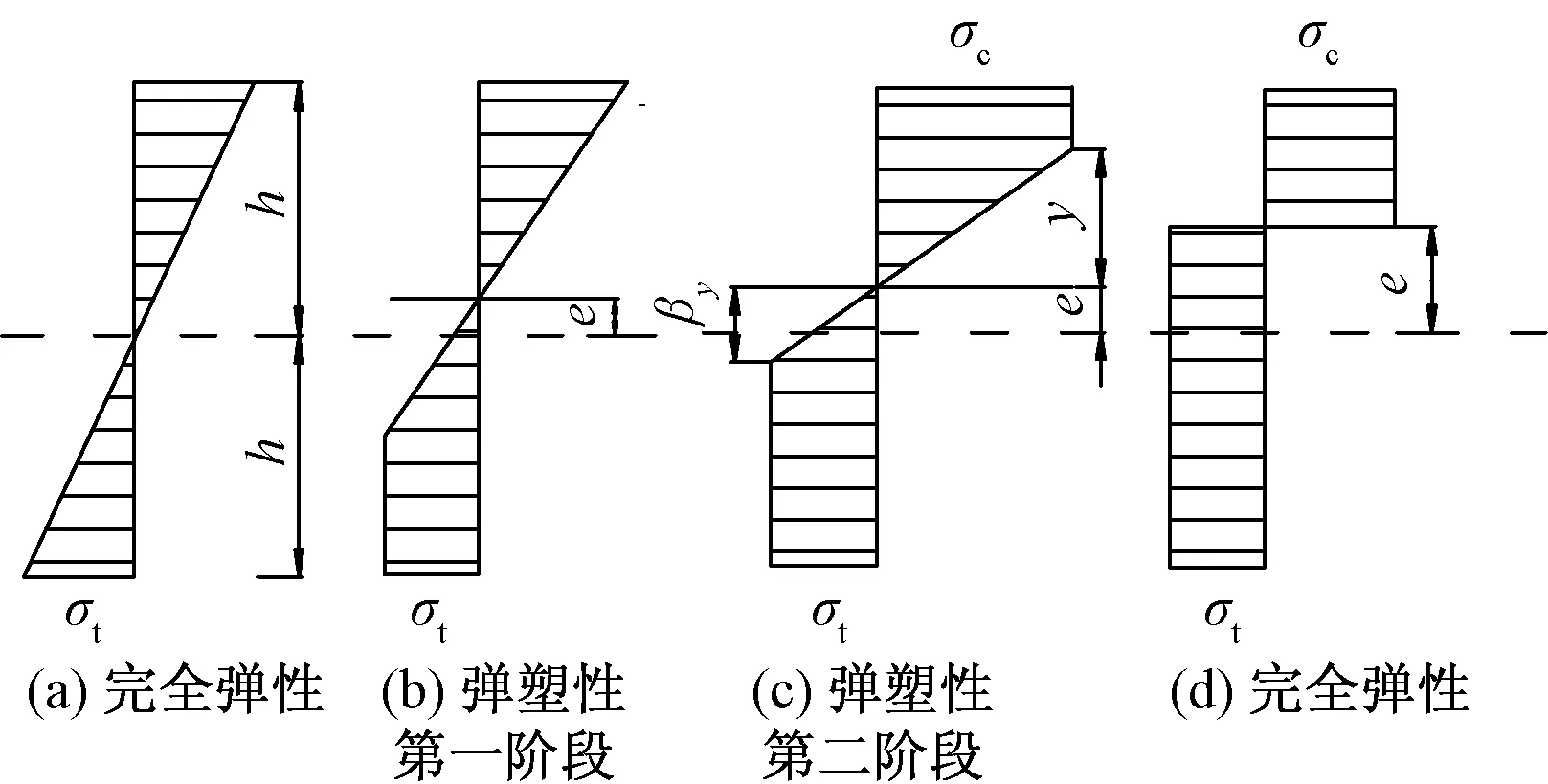
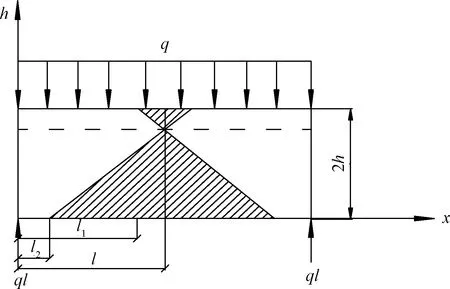
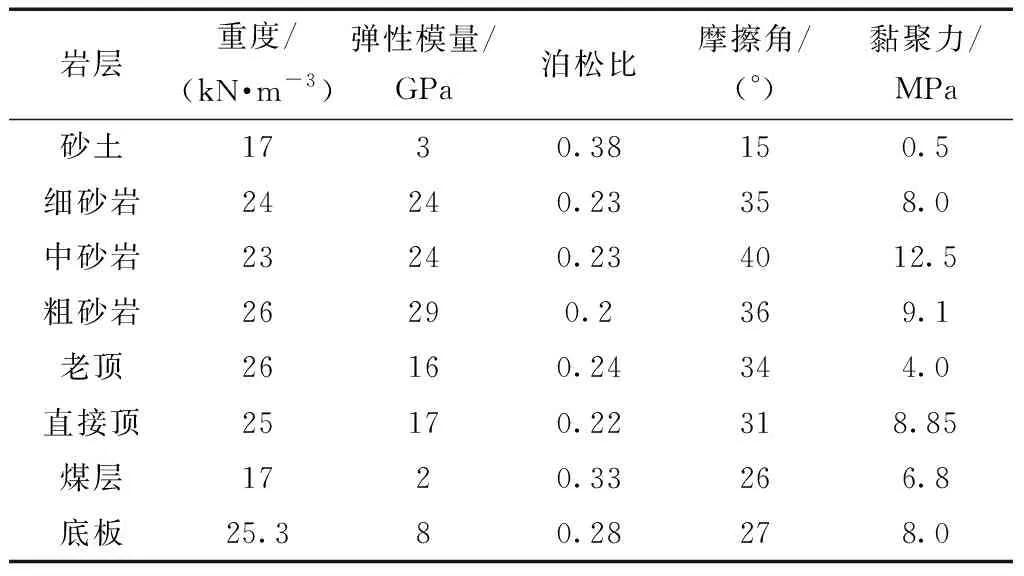
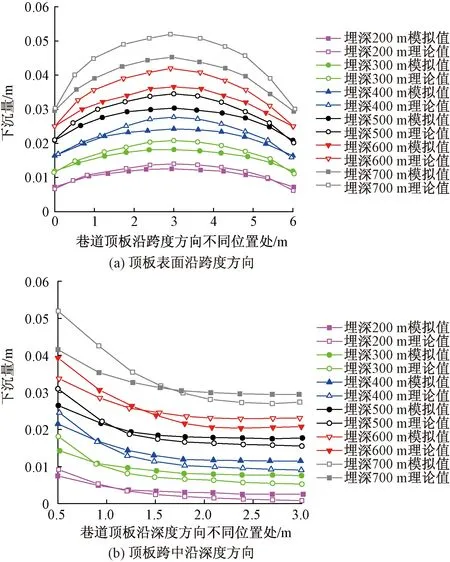
由式(3)可知，当h≥he时，顶板梁处于弹性状态；当h

1.3 顶板梁弹塑性状态分析

为求得顶板梁在弹塑性状态下的挠曲方程，首先对顶板梁截面弹塑性演化过程进行分析，求得不同阶段梁截面所对应的弯矩。继而根据平截面假定得到顶板梁在弹塑性状态下的挠曲方程。在顶板梁材料本构关系的简化模型中，考虑巷道顶板围岩抗拉屈服强度小于抗压屈服强度的特点，因此令β=σt/σc≤1(σt、σc分别为顶板围岩的极限抗拉强度和极限抗压强度)。

1.3.1 顶板梁截面弹塑性分析

顶板梁截面上应力分布随着煤岩体材料进入塑性阶段的不同有以下几种情况，如图2所示。当梁截面所受弯矩大于围岩的弹性弯矩时，如图2(b)所示，顶板梁截面受拉侧应变将继续增大，应力值σt不再增加，截面受拉侧塑性区逐渐扩大，此时为保证梁截面上正应力之和为零，中性轴开始偏离，设偏离距离为e；当顶板梁截面受压侧最大压应力达到σc时，该侧也将进入塑性状态，如图2(c)所示，设顶板梁上层弹塑性区交界处距梁中性轴的距离为y，下层弹塑性区交界处距梁中性轴的距离为βy。

图2 顶板梁截面弹塑性阶段演化图Fig.2 Elastoplastic stage evolution diagram of roof beam section

当梁截面处于弹性状态时，如图2(a)所示，截面拉应力达到σt时，顶板梁截面弹性极限弯矩M′e为[11]

(5)

当梁截面处于弹塑性第二阶段时，如图2(c)所示，离心距e及截面弯矩M为

(6)

(7)

当y=0时，即梁截面全部处于塑性状态，如图2(d)所示，此时梁截面塑性状态弯矩Mp为

(8)

1.3.2 弹塑性状态下顶板梁的挠度求解

根据巷道顶板梁截面不同的受力状态，可将整根梁分为3部分，如图3所示(为简便起见仅考虑l范围内的部分梁)，分别为：完全弹性区(0≤x≤l2)、弹塑性区(l2≤x

图3 顶板梁在极限状态时的弹塑性分布Fig.3 Elastic-plastic distribution of roof beam in the limit state

当梁截面处于弹塑性状态时(l2≤x

(9)

代入式(7)可得

(10)

由式(9)、式(10)可得到顶板梁受压区弹塑性区交界处距梁中性轴的距离为

(11)

当顶板梁受压区处于弹性极限状态(y=h)时，根据式(11)可知x=l(1-A)。故可得l1=l(1-A)，l2=βl(1-A)。

因此，顶板梁在塑性状态下挠曲微分方程分别为

0≤x≤βl(1-A)时，

(12)

βl(1-A)≤x≤l时，

(13)

式(12)、式(13)的边界条件：顶板梁端挠度为零；跨中转角为零；顶板梁在x=βl(1-A)处的转角和挠度相等。考虑到梁材料为煤岩体，取β=1/6，故可得顶板梁在塑性状态下挠度方程为

(14)

根据式(14)可知，顶板梁的挠度在不同位置处是不同的，在顶板梁跨中位置x=l处挠度最大，由跨中向两帮递减。同时，巷道埋深越大，顶板梁产生的挠度越大。

当x=l时，代入式(14)中可得巷道顶板梁塑性状态下跨中挠度ωp为

(15)

根据式(8)可得顶板梁在塑性状态下跨中的最大弯矩Mmax为

Mmax=Mp=2.63ql2

(16)

以顶板梁跨中截面上的最大正应力不超过围岩的极限抗压强度为条件，得到巷道顶板最大塑性区高度hp与围岩的极限抗压强度的关系，即

(17)

根据式(17)可得到处于塑性极限状态下的梁高为

(18)

根据以上分析可知，当h≥he时，顶板梁处于弹性状态，此时顶板梁跨中挠度方程为式(4)。

当h≤hp，顶板梁处于塑性状态，此时顶板梁跨中挠度方程为式(15)。

当he

(19)

当h不同时，根据式(4)、式(15)、式(19)可得到处于不同状态、不同深度处顶板围岩跨中部位的下沉变形值。顶板围岩下沉变形沿深度方向随h的增大逐渐减小，顶板围岩表面处下沉变形值最大，向岩体内部逐渐减小，在无限远处(h→)变为0。

2 模拟验证

2.1 工作面条件

柠条塔煤矿s12001运输巷道埋深200 m，巷道断面尺寸宽6 m，高4 m，煤层平均厚度4.3 m；老顶一般厚度为 12.90 m，以粗粒砂岩为主；直接顶一般厚度为9.55 m,以细粒砂岩为主；低板一般厚度为8.75 m，为碳质泥岩为主。岩层物理力学参数如表 1所示。

表1 煤岩体物理力学参数Table 1 Physical and mechanical parameters of coal and rock mass

2.2 模型建立

采用有限元数值模拟软件(FLAC3D)进行模拟计算，建立模型采用zone单元，三维模型的边界条件取为：四周与底部采用固定边界，上部为自由边界巷道。巷道断面取高4 m、宽6 m，埋深分别取200、300、400、500、600、700 m时对顶板下沉变形进行分析，建立的模型如图4所示。

图4 FLAC3D数值模拟计算模型Fig.4 FLAC3D numerical simulation model

2.3 模拟结果分析

结合柠条塔煤矿s12001胶运顺槽工作面开采条件，将理论所计算的顶板围岩表面不同位置处的下沉量(设定半梁高h为1.4 m)和顶板围岩跨中位置沿深度方向不同位置处的下沉量(设定半梁高h依次为1.4 m、1.5 m、1.6 m、…)与模拟结果进行对比，分别如图5和图6所示，图6以巷道埋深200 m和300 m为例，发现，当巷道尺寸一定时，随着埋深的增加，巷道顶板整体下沉变形值不断增加；在顶板围岩表面不同位置处，沉降值并不相等，顶板中间部位沉降值最大，向顶板两帮逐渐递减；巷道顶板表面沉降值最大，向岩体内部逐渐减小；数值模拟所揭示的巷道顶板下沉变形规律与理论计算值以及现场监测所反应出的规律一致。在中浅埋深(≤500 m)的情况下，理论计算结果与模拟结果相差不大；埋深较大时(>500 m)，与模拟结果相比，理论计算结果偏大。因此，理论计算式适用于中浅埋深情况下顶板下沉量的计算。

图5 巷道顶板下沉位移曲线对比Fig.5 Comparison of roadway roof subsidence displacement curves

图6 位移变形云图Fig.6 Displacement deformation cloud diagram

3 工程实例

3.1 测点布置与数据采集

测站布置在柠条塔煤矿s12001胶运顺槽工作面巷道。顶板离层仪监测点安装位置分别距顶板跨中部位0.5、1.0、1.5、2、2.5、3、4、5、6 m。收敛计测点安装位置为距左帮部0.5、1.5、2.5、3、3.5、4.5、5.5 m处，实测离层曲线及顶板表面下沉量分别如图7和图8所示。

图7 实测顶板离层变形曲线Fig.7 Measured roof separation deformation curve

图8 实测顶板下沉位移量Fig.8 Actual displacement of roof subsidence

3.2 监测结果分析

现将巷道变形稳定后，顶板跨中部位沿深度方向不同位置的下沉量以及沿跨度方向不同位置处的下沉量绘制为曲线，并与理论计算结果以及模拟结果相比较，如图9所示。由图9可知，巷道顶板下沉量与理论计算结果以及数值模拟结果基本一致。结果表明，在中浅埋深(≤500 m)时，根据理论确定出的巷道顶板下沉量较为可靠。

图9 顶板沿跨度方向及深度方向不同位置处下沉变形对比Fig.9 Comparison of roof subsidence deformation at different positions along the direction of span and depth

4 结论

(1)考虑煤岩体抗压强度大于抗拉强度的特点，根据弹塑性理论，建立了顶板梁弹塑性模型。对矩形截面顶板梁的弹塑性全过程进行分析，得到矩形巷道顶板围岩表面以及跨中部位沿深度方向不同位置处的挠度曲线方程。

(2)理论计算式所揭示的顶板围岩变化规律为：①当巷道尺寸一定时，随着埋深的增加，巷道顶板整体下沉量不断增加；②在顶板围岩表面不同位置处，下沉量并不相等，顶板跨中部位下沉量最大，向两帮逐渐递减；③巷道顶板围岩表面下沉量最大，向岩体内部逐渐减小。

(3)使用有限元数值模拟软件(FLAC3D)，结合柠条塔煤矿的工程条件，当巷道断面高4 m、宽6 m，埋深分别为200、300、400、500、600、700 m时，对巷道顶板下沉变形进行了模拟。可以发现在中浅埋深(≤500 m)时，理论计算的下沉量与数值模拟的结果相差不大。表明在中浅埋深的情况下，按理论计算式得出的巷道顶板围岩下沉变形有较好的适用性。

(4)通过对柠条塔煤矿s12001运输巷道顶板围岩下沉变形进行监测，对理论计算结果的可靠性进行评估。监测结果与理论计算结果一致，验证了在中浅埋深下理论计算式的可靠性。