分形结构及尺度对粒子扩散行为的影响

曹馨予, 孙洪广*, 靳 垚, 李志鹏

(1.河海大学水文水资源与水利工程科学国家重点实验室， 南京 211100; 2.河海大学力学与材料学院， 南京 211100)

随着社会经济的发展，人类生产和生活过程中产生的污染物通过各种途径进入土壤。如果污染物浓度超过土壤自净能力，则土壤质量和功能会发生改变，最后对人类及其他生物的生存和发展造成危害。调查结果显示，中国部分地区土壤问题严峻，耕地土壤环境质量堪忧，土壤污染防治迫在眉睫[1]。

1965年Mandelbrot[2]首次提出了分形的概念，并认为自然界中存在大量的自相似分形结构。随后经过一系列研究分析表明,土壤是一种具有分形特征的多孔结构介质[3-5]。污染物在土壤中的输运行为受到介质结构和尺度的影响[6-7]。对于实际的土壤等多孔介质，Katz等[8]也通过电镜实验证实，它们的结构往往具有不同尺度的非均匀性,并具有分形特征。

20世纪初期，Einstein[9]建立了布朗随机运动理论，提出了溶质扩散的位移二阶矩表达式。布朗运动可以视为与时间有关的随机分形。在欧式空间，根据随机行走理论，粒子布朗运动的空间分布函数为高斯分布[10]。溶质扩散的传统研究方法主要基于Fick扩散定律。但是由于土壤等复杂多孔介质不满足均匀介质假设，Fick定律不再适用。因而，从20世纪 70 年代开始，考虑介质非均匀性对粒子随机运动影响的随机行走反常扩散模型得以建立和发展[11-12]。复杂介质中粒子随机运动的平均扩散位移r2(t) 的一般形式可以表述为〈r2(t)〉=t2H[13-14],其中H为Hurst数。H=0.5表示正常扩散；H<0.5代表次扩散,等待时间发散而跳跃步长收敛的随机行走过程可视为此类运动；H>0.5时的扩散称为超扩散，其特征为等待时间收敛而跳跃步长发散，如湍流中粒子的随机运动[15]；H=1.0表示弹道扩散[16-17]。

随着分形理论的发展，中外研究者以分形理论为基础，构建了多种多孔介质分形模型。例如，Turcio等[18]构造了一种分形模型，得到多孔介质中有效渗透率表达式；施明恒等[19]通过构建分形导热模型,导出了多孔泡沫材料中分形导热系数的计算公式；周祥春等[20]建立了多孔介质分形模型，研究了分形维数等因素对粒子扩散行为的影响；Cai等[21]提出一种新型变孔径三维分形模型，对页岩地层中流体流动机理进行了分析；Li等[22]通过构造分形多孔介质模型探究了多孔介质内部结构与有效应力之间的关系。已有研究表明[23-24]，构造人工的分形多孔介质模型可以为探索复杂介质溶质扩散机理和理解污染物输运机制提供有效帮助。

现首先构造两种结构和尺度各异的Sierpinski地毯分形模型模拟真实的土壤多孔介质结构[25]。进而通过粒子在分形结构中的随机行走过程模拟探索污染物在土壤中的输运过程[26-27]。最后通过粒子在两种分形结构中扩散行为的对比分析，探究分形结构及尺度差异对粒子扩散行为的影响。

1 分形结构模型

1.1 土壤分形结构

土壤是由不同形状和大小的固体组分及孔隙以一定形式连接而成的多孔介质[28]。已有研究证实[29-31]，许多土壤结构具有分形结构特征，表现出自相似性。因此，将采用Sierpinski地毯这一“人工构造分形体”模型来表征自然界中实际土壤的介质结构。

1.2 两种分形结构

目前土壤分形结构的相关研究[32-34]选取的分形结构大多为单块分形结构，这类分形结构一定程度上能够反映土壤这类多孔介质的异质性。然而实际观测中发现,由于采样土壤所处的环境各异，实验室土样与自然环境土样的尺度差别不容忽视，这些因素会影响预测结果的准确性[35-36]。为准确模拟污染物在土壤中的输运行为，建立两种分形结构：单块分形结构及四块拼接分形结构，目的是考察结构及尺度对粒子扩散行为的影响。其中，四块拼接分形结构是一种内含重复分形结构单元的模型。基于这种拼接分形结构模型，将着重探究粒子的扩散问题。表1列举了上述两种分形结构的孔隙分形维数及空间尺度。其中孔隙分形维数由盒计数法计算得到。

表1 两种分形结构的孔隙分形维数及空间尺度Table 1 Fractal dimensions of pores and spatial scales of two types of fractal structure

1.3 拼接分形结构的构造

四块拼接分形结构的构造方法如下：

步骤1构造单块分形结构。

通过MATLAB软件建立一级Sierpinski地毯分形结构。应用迭代方法，构造四级Sierpinski地毯分形结构，如图1(a)所示。

步骤2构造四级拼接分形结构。

选取如图1(a)所示的四级分形结构。通过软件进行图像处理，生成四块拼接分形结构，如图1(b)所示。

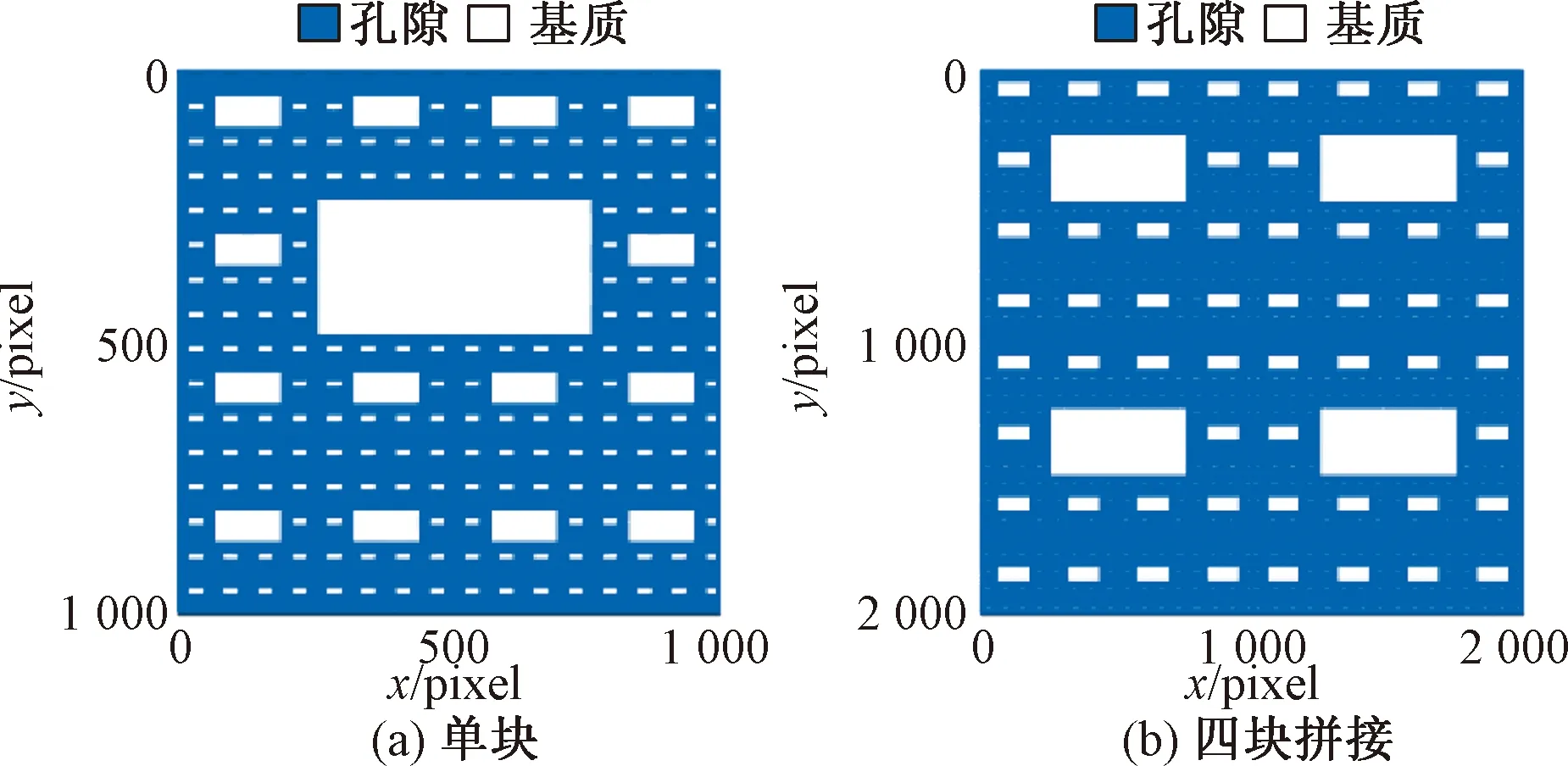
图1 两种分形结构模型Fig.1 Two models of fractal structure

1.4 粒子行走过程描述

将分形结构中心位置作为随机行走起始点，在起始点处投放5 000个粒子。采用全瞎的蚂蚁随机行走模式模拟扩散过程。假定粒子在孔隙与基质中均能够扩散[37]，在基质中的行走步长为1 pixel，在孔隙中的行走步长为5 pixel。只允许粒子在分形结构边界范围内随机运动。若粒子行走一定步数后，位置超出边界范围，则该粒子停止运动，停留在边界处，待下一步随机跳跃时，从停留处重新随机跳跃。若下一步的行走位置超出边界，则重复上述过程，若未超出边界，则按规则正常跳跃。所有粒子完成规定的行走步数记为一次有效的行走过程，记录所有粒子随机行走过程中每一步的位置坐标。具体的数值模拟算法流程,如图2所示。

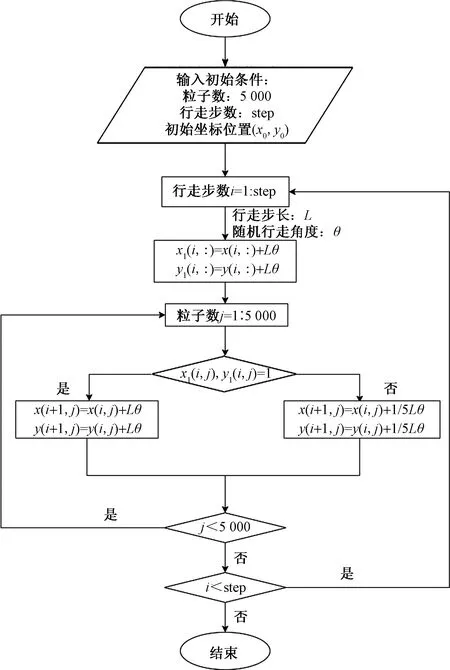
图2 数值模拟程序算法流程图Fig.2 Algorithm flow chart of numerical simulation program

2 粒子扩散过程模拟

2.1 单块分形结构中粒子扩散过程模拟

在单块分形结构的中心位置(500，500)处投放5 000个粒子。记录粒子行走500～10 000步的平面空间分布、密度分布及粒子扩散均方位移与时间的关系。

粒子行走1 500、2 500、6 000、10 000步后的空间分布，如图3所示。由图3可知，随着行走步数增加，粒子的扩散区域逐渐增大。由于受到分形结构中基质的阻碍作用，基质中的粒子数相对较少。

从图3(a)中观察到，粒子行走1 500步后，未出现粒子扩散至分形结构边界处，扩散区域较小，此时粒子的扩散过程只受到结构内基质的阻碍作用。从图3(b)中发现，粒子行走2 500步后，扩散区域进一步增大，少量粒子扩散至结构边界。此时粒子的扩散受到基质和边界效应的共同影响。由图3(c)、图3(d)可知，粒子行走6 000、10 000步后，大量粒子扩散至结构边界，边界效应对粒子扩散过程的影响逐渐增大。

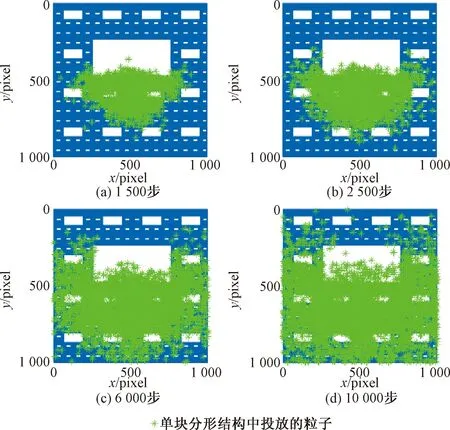
图3 单块分形结构中粒子行走1 500、2 500、6 000、10 000步后的空间分布Fig.3 The spatial distribution of particles after 1 500, 2 500, 6 000, 10 000 steps in single fractal structure

粒子行走1 500、2 500、6 000、10 000步后的密度分布如图4所示。可知，粒子的密度分布是与分形结构有关的不均匀分布。在起始处粒子密度最大，随着粒子行走步数增加，密度分布范围逐渐增大。由于基质对粒子扩散行为的阻碍作用，基质中的粒子密度较小。大量粒子的平面密度分布在左右方向上大致对称。

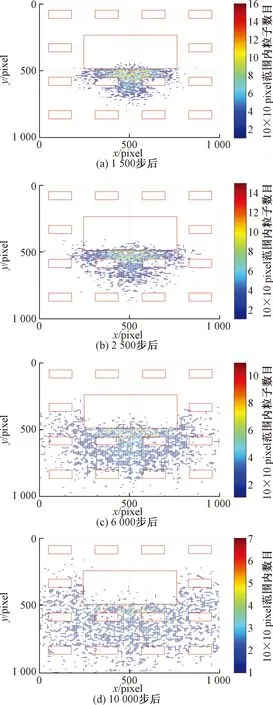
图4 单块分形结构中粒子行走不同步数后的密度分布Fig.4 The density distribution of particles after different steps in single fractal structure

图5为粒子行走1 500、2 500、6 000、10 000步后的均方位移与时间的关系曲线。表2列举了粒子行走500～10 000步时对应的Hurst参数值。

由图5和表2分析可知，在分形结构尺度为1 000 pixel×1 000 pixel、孔隙分形维数为1.90的单块分形结构中，粒子行走1 500步前，Hurst值小于0.5。此时粒子的扩散只受到基质对它的阻碍作用，粒子的扩散行为表现为次扩散；粒子行走1 500～6 000步时，Hurst值增大到0.5附近波动。这是由于当粒子行走到分形结构边界时，边界效应限制了粒子的行走方向,这相当于缩小了粒子在孔隙与基质中的步长比。粒子的扩散行为出现短暂的正常扩散现象；粒子行走6 000～10 000步时，Hurst值急剧减小。该阶段大量粒子行走至边界处，边界效应对粒子扩散过程的影响增大。由于空间尺度较小，粒子位移无法进一步增加，输运行为受到阻滞，Hurst值减少。

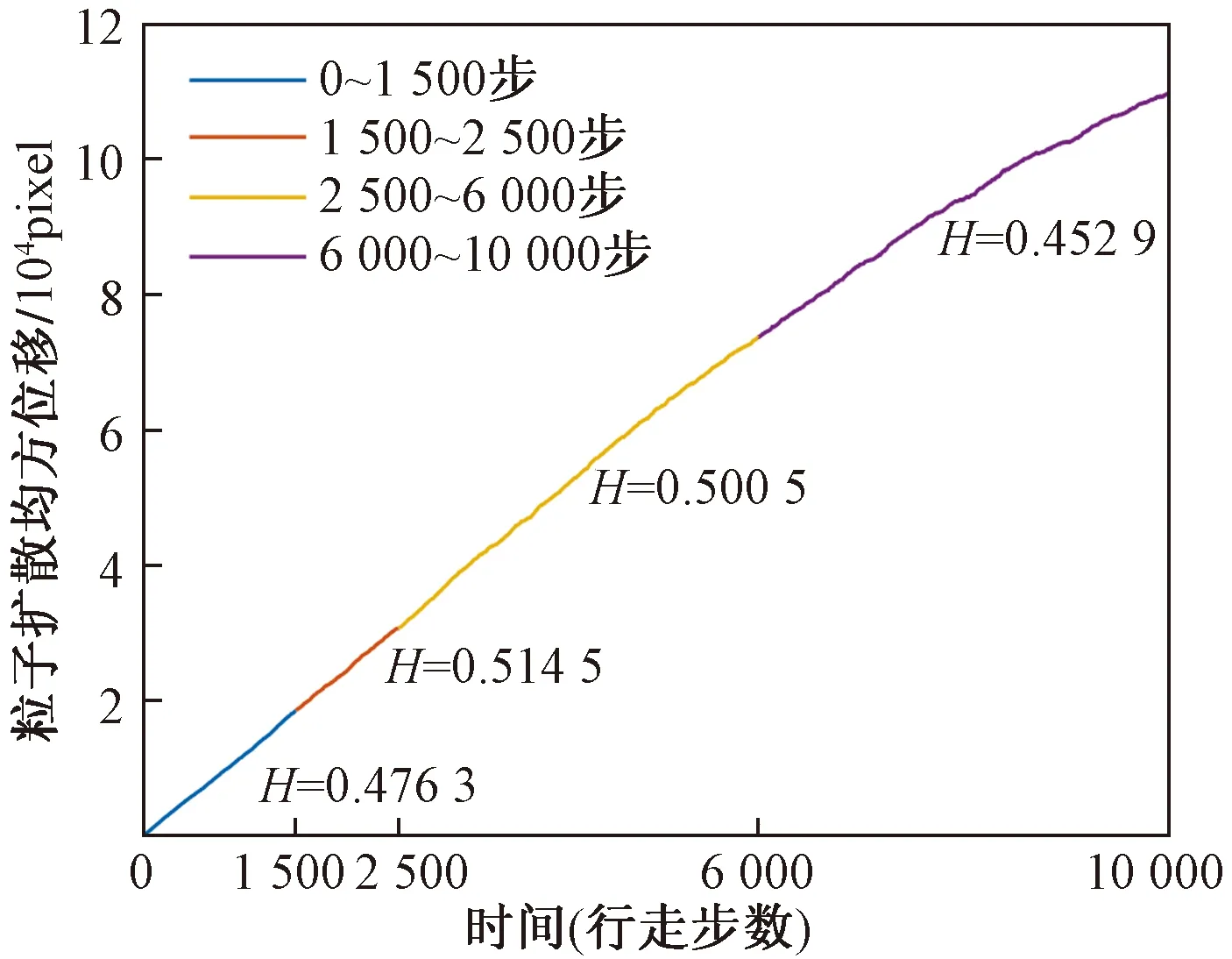
图5 单块分形结构中粒子扩散均方位移与时间的关系曲线Fig.5 The relationship between mean square displacement and time of particles in single fractal structure

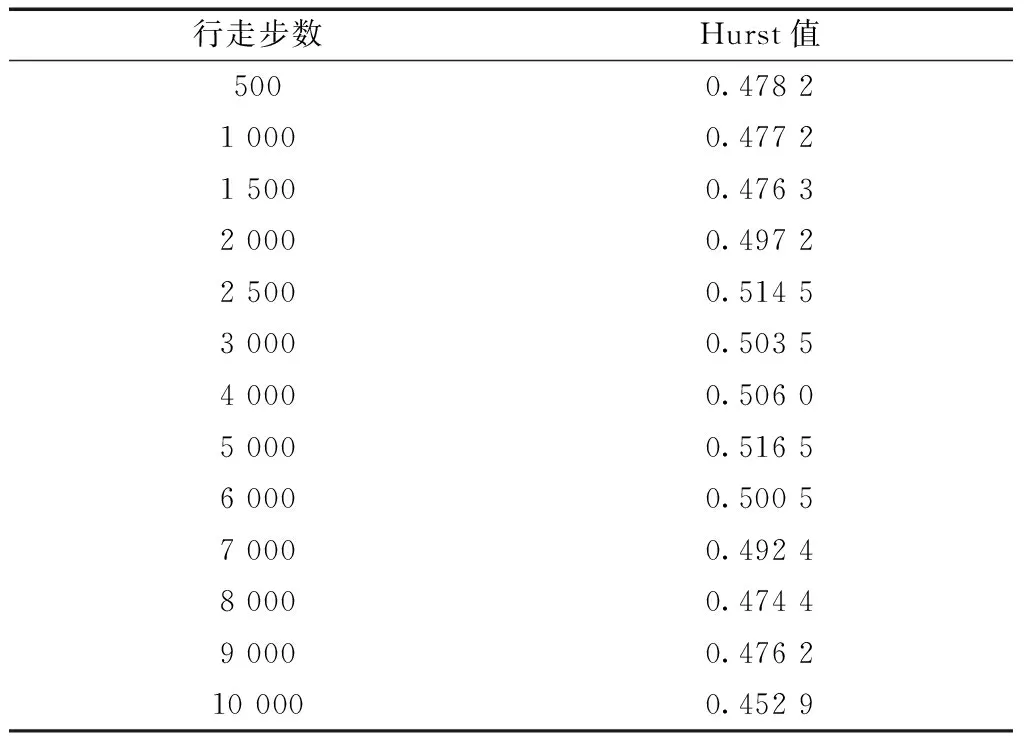
表2 单块分形结构中的Hurst值

2.2 四块拼接分形结构中数值模拟

在四块拼接分形结构中心位置(1 000，1 000)处投放5 000个粒子。记录粒子行走500～10 000步的空间分布、密度分布及粒子扩散均方位移与时间的关系。

图6表示粒子在四块拼接分形结构中行走2 500、7 000、10 000步后的空间分布。从图6可观察到，粒子的空间分布范围随着行走步数的增加逐渐增大。粒子在孔隙中的扩散速度较在基质中更快。由于此分形结构呈对称分布，粒子的空间分布也呈对称状态。

从图6(a)中观察到，粒子行走2 500步后仍未行走至边界，粒子的扩散过程只受结构内基质影响。由图6(b)可知，粒子行走7 000步后，少量粒子行走至分形结构边界，此时粒子的扩散过程不仅受到分形结构内基质的阻碍作用，还受到边界效应的影响。由图6(c)中观察到，粒子行走10 000步后，行走至边界处的粒子数逐渐增多。

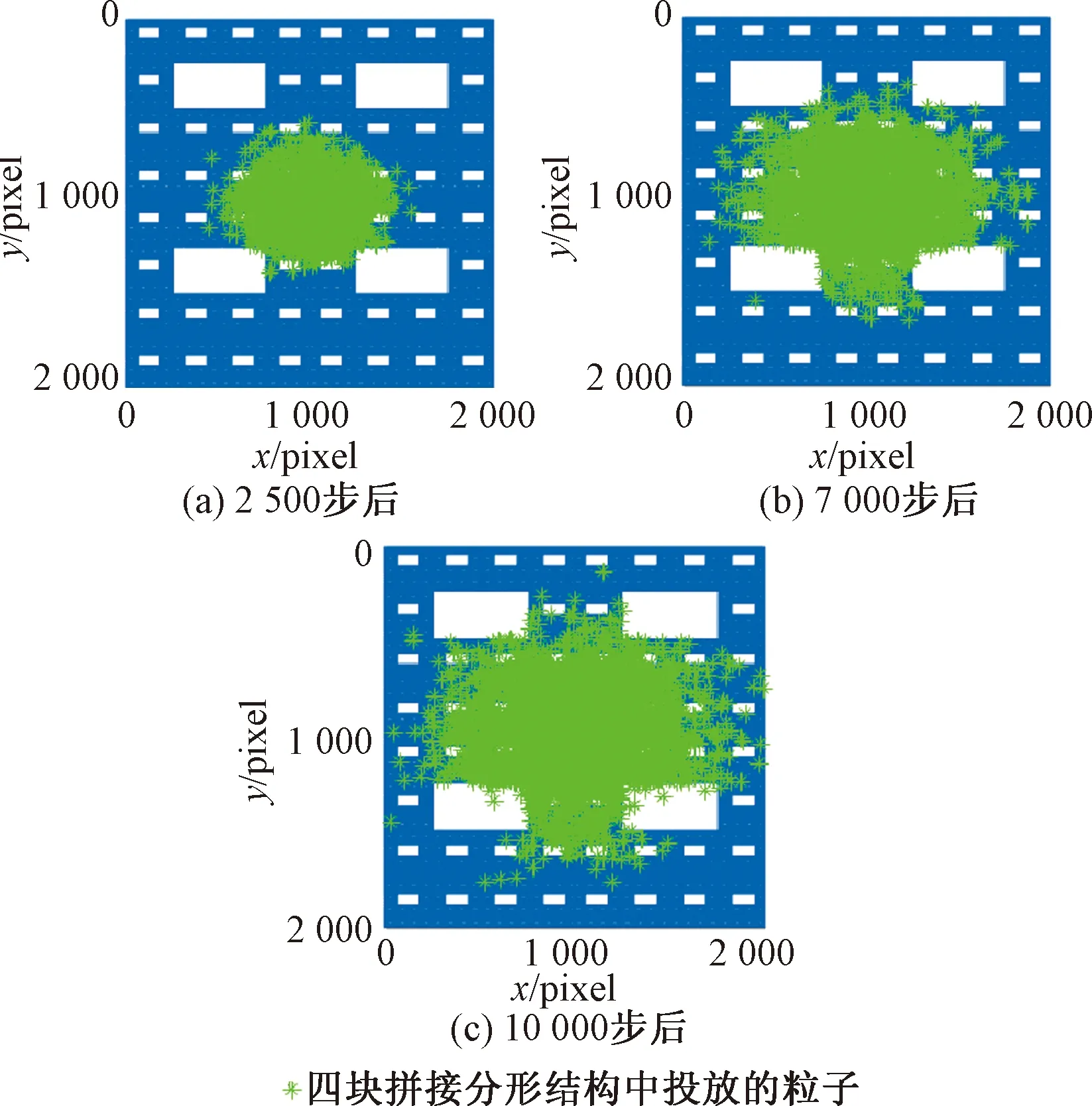
图6 四块拼接分形结构中粒子行走不同步数后的空间分布Fig.6 The spatial distribution of particles after different steps in four spliced fractal structure

粒子行走2 500、7 000、10 000步后的密度分布如图7所示。从图7中观察到，粒子的密度分布近似对称。起始点周围粒子密度较大，并由中心位置向四周逐渐减小。随着行走步数增加，粒子扩散位移及密度范围增大。同时从图7中可以观察到，基质对粒子扩散过程的阻碍作用明显。

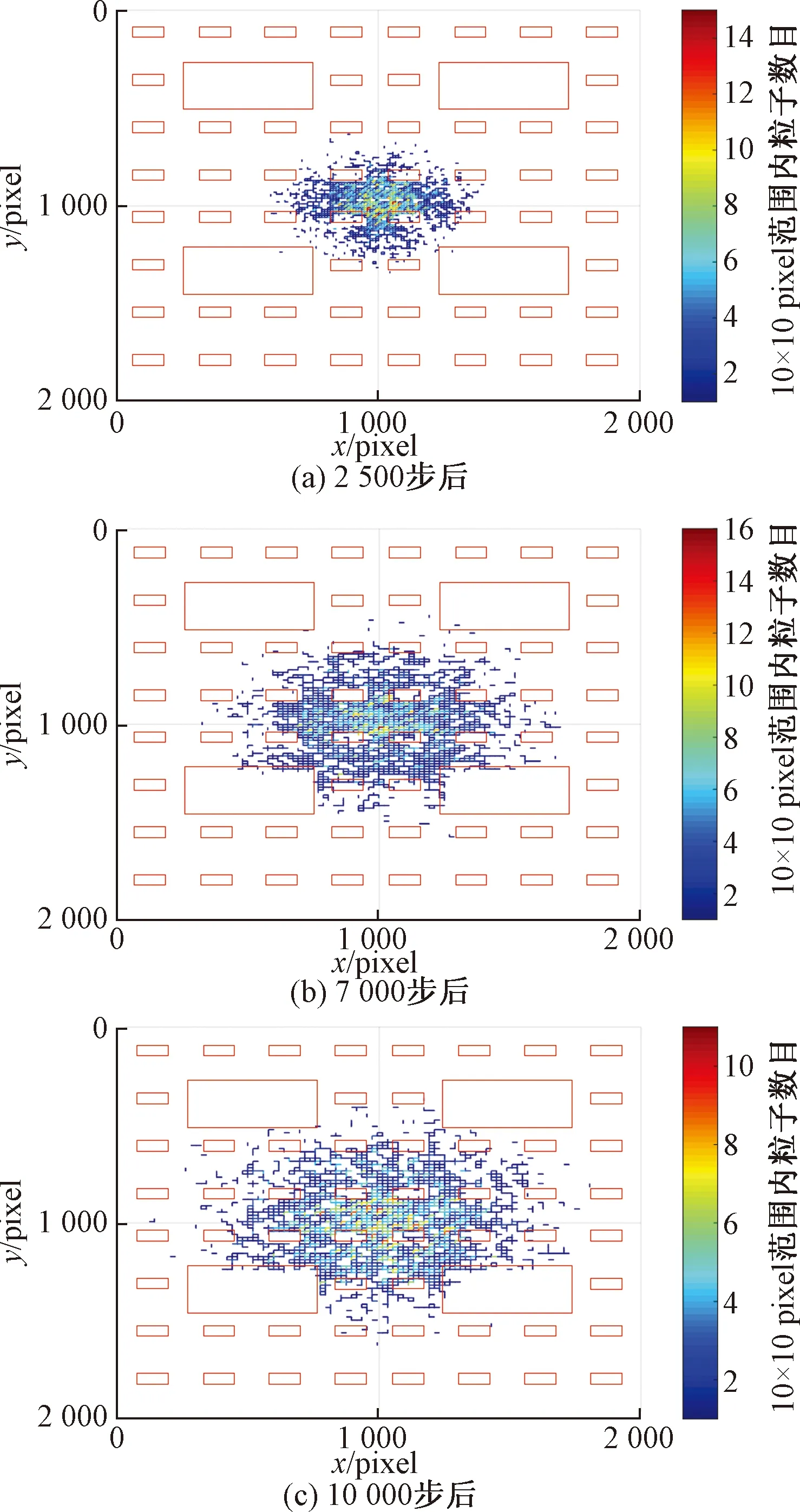
图7 四块拼接分形结构中粒子行走不同步数后的密度分布Fig.7 The density distribution of particles after different steps in four spliced fractal structure

图8为粒子行走2 500、7 000、10 000步后的均方位移与时间的关系曲线。表3列举了粒子行走500～10 000步时对应的Hurst值。

由图8和表3分析可知，在分形结构尺度为2 000×2 000 pixel、孔隙分形维数为1.98的四块拼接分形结构中，粒子行走500～10 000步的过程中，Hurst值均小于0.5且数值波动较小，扩散行为均呈现次扩散现象。

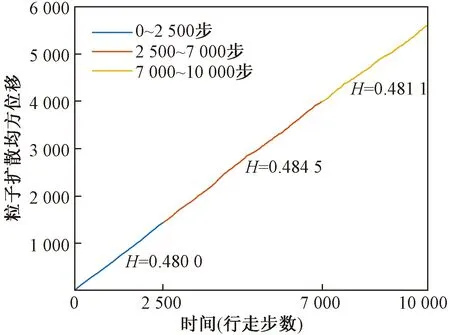
图8 四块拼接分形结构中粒子扩散均方位移与时间的关系曲线Fig.8 The relationship between mean square displacement and time of particles in four spliced fractal structure

2.3 数值模拟结果的有效性

为论证上述模拟结果的有效性，将模拟条件设定为：在单块分形结构中心位置投放5 000个粒子，采用“全瞎”的蚂蚁随机行走模式模拟扩散过程。假定粒子在孔隙中的行走步长为1 pixel，在基质中不能行走。扩散过程中没有粒子行走至分形结构边界。

记录粒子行走5 000、10 000、20 000步后的扩散均方位移与时间的关系。如图9所示，通过数值模拟，计算得到Hurst参数的平均值为0.477 0。该模拟结果同与本文模拟条件相同的相关研究的数据：0.462±0.003[38]、0.477±0.004[39]接近，且处于95%的置信限内。因此，数值模拟结果的有效性可以在一定程度上得到验证。

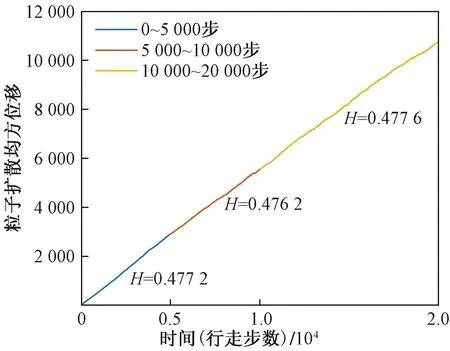
图9 粒子扩散均方位移与时间的关系曲线Fig.9 The relationship between mean square displacement and time of particles

3 结果与讨论

由上述模拟结果可知，粒子在单块分形结构与四块拼接分形结构中的扩散行为存在差异。当粒子行走2 500步时，在单块分形结构中，已存在粒子扩散至边界，其扩散行为受基质和边界的共同影响；而在四块拼接分形结构中，此时粒子并未扩散至边界，粒子未受到边界效应影响。行走7 000、10 000步后，虽然已出现扩散至边界的粒子，但与单块分形结构中的行走过程相比，边界效应对其扩散行为的影响较小。但由于单块分形结构及四块拼接分形结构的尺度及结构均不相同，为分别研究结构和尺度对污染物输运过程的影响，需对粒子在面积放大四倍的单块分形结构中的扩散行为进行讨论。

面积放大四倍的单块分形结构的空间结构与单块分形结构相同。其空间尺度为 2 000 pixel×2 000 pixel，与四块拼接分形结构的尺度相同。通过粒子在面积放大四倍的单块分形结构中的扩散模拟，可以得到粒子在此结构中行走500步至10 000步时对应的Hurst值，列于表4。由表2～表4所列的Hurst值可以得到粒子在上述三种结构中随行走步数变化的Hurst值折线图，如图10所示。

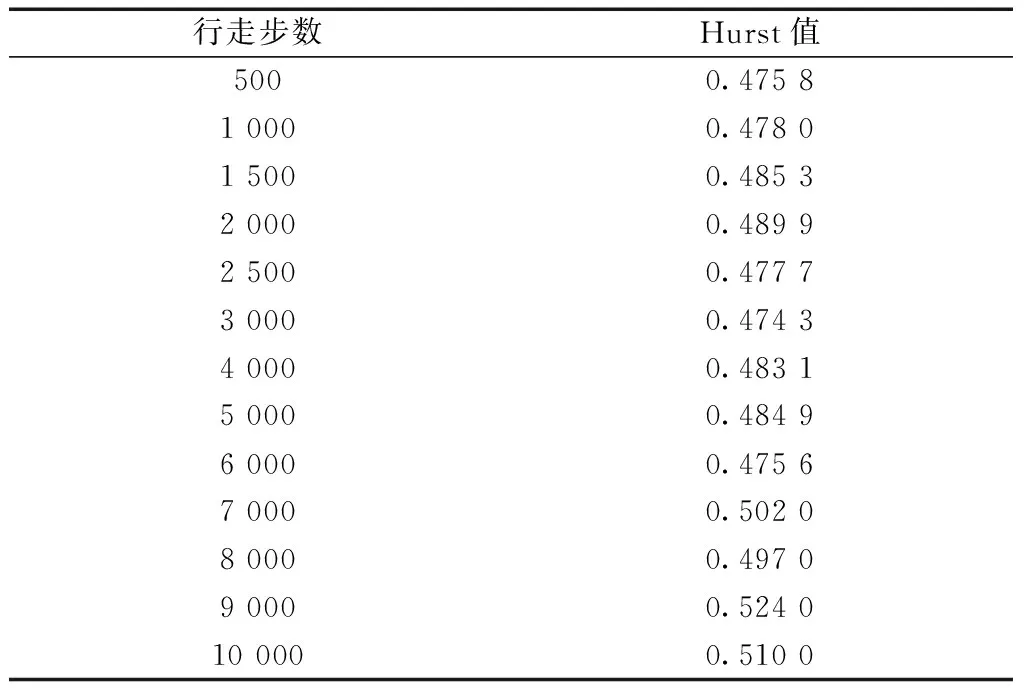
表4 面积放大四倍的分形结构中的Hurst值Table 4 Hurst value in the single fractal structure with four times larger area

由图10分析可知，在单块分形结构中，随着行走步数增加，Hurst值先在小于0.5处保持较小波动，然后增大到0.5附近波动后急剧减小；在面积放大四倍的单块分形结构中，随着行走步数增加，Hurst值先在小于0.5处波动，然后增大到0.5附近；在四块拼接分形结构中，随着粒子行走步数增加，Hurst值稳定在小于0.5处。由上述分析可知，粒子在三种分形结构中的扩散行为均存在差异。分形结构及空间尺度的差异影响粒子的扩散行为。在空间尺度较小的单块分形结构中，粒子的扩散行为会在短时间内发生变化，其扩散过程更容易受到结构内部及结构边界的共同影响。

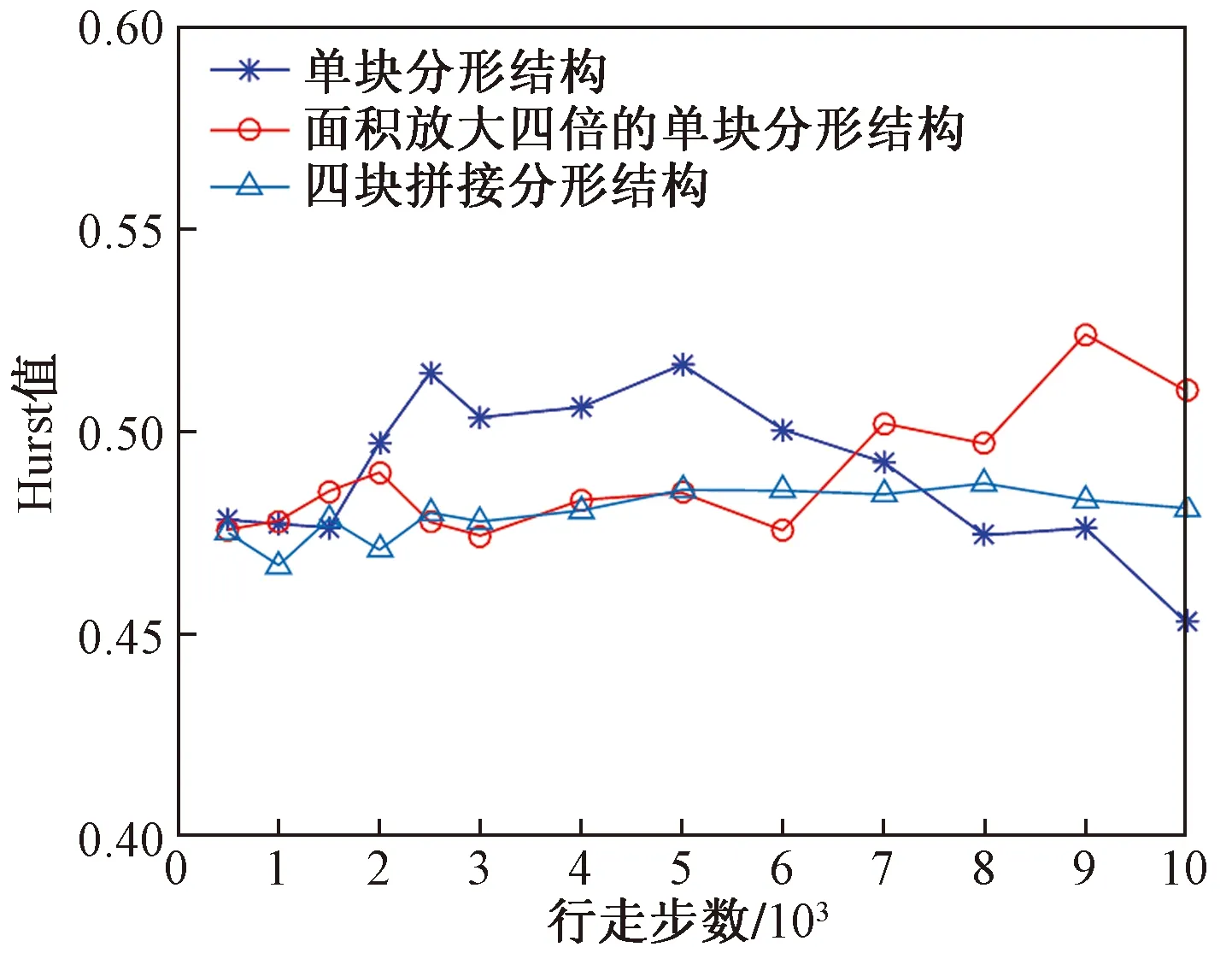
图10 三种分形结构中随粒子行走步数变化的Hurst值折线图Fig.10 The line chart of Hurst value varying with steps taken by particles in three fractal structures

4 结论

通过建立两种土壤分形结构：单块分形结构、四块拼接分形结构，分别考察了尺度和结构差异明显的多孔介质结构。通过粒子在这两种分形结构中的随机行走过程模拟，分析了污染物在土壤结构中的扩散行为，研究并得出以下结论。

(1)粒子在单块分形结构、四块拼接分形结构中的扩散行为受分形结构中基质的阻碍作用，粒子的扩散行为呈次扩散现象。当粒子行走至分形结构边界后，其扩散行为受边界影响，短暂向正常扩散行为过渡。

(2)分形结构的尺度差异对粒子的扩散行为有明显影响。当粒子的扩散过程未受到边界效应影响时，小尺度与大尺度分形结构中的粒子扩散行为均呈现次扩散现象。然而，当粒子的扩散过程受到边界效应影响时，在小尺度分形结构中，粒子扩散行为在短时间内发生明显变化，由次扩散现象变为正常扩散现象再过渡到次扩散现象；而在大尺度分形结构中，粒子的扩散行为在相当长的时间内保持稳定，扩散行为保持次扩散输运状态。

(3)不同的分形结构会导致粒子的扩散行为产生较大差异。若分形结构的空间尺度一定，在单块分形结构中，粒子在受到边界效应影响时扩散行为会发生明显变化，由次扩散现象过渡为正常扩散现象；而这种变化在内含重复分形结构单元的拼接分形结构中并不明显，次扩散行为相对稳定。因此，由于自然环境中的土壤结构各异，选择合适的分形结构模型才能够更准确的模拟污染物等溶质在土壤中的输运行为。