基于地形分区的黄土丘陵区土壤有机质空间预测

张 婧，毕如田，丁皓希，文伟杰，荆颖蔷

（山西农业大学资源环境学院，山西太谷 030801）

土壤有机质作为表征耕地肥力大小的重要指标，其含量在农作物的整个生长过程中发挥着非常重要的作用[1]。土壤有机质具有较强的时空变异性，其空间规律一直是许多学者研究的热点问题。大量研究表明，土壤有机质的空间变异会受各种因素的影响，如地形、土壤类型、耕作模式、土地利用方式等[2-3]。但是关于多种因素协同对有机质的空间影响目前还少有研究。

Kriging 空间插值法是一种土壤属性空间预测最普遍的方法[4-5]，但是普通Kriging 插值在平坦、地形单一的区域预测结果较好，而在复杂地区插值效果一般。随着科学技术的进步，Kriging 插值引入其他参数作为辅助变量的方法已经得到广泛的应用，而且预测精度较高。例如，徐占军等[6]基于分区Kriging 插值法对煤炭开采沉陷区土壤有机碳含量进行空间预测，结果显示，分区Kriging 预测结果的精度比普通Kriging 预测的更高；MISHRA 等[7]以印第安纳州为研究区，利用普通Kriging 模型和剖面深度分布函数分别预测了表层土壤有机碳的含量，结果表明，剖面深度分布函数预测精度高于普通Kriging 模型。

地形是引起土壤有机质空间变异的主要因子，而地形起伏度是表征地形特征的重要参考指标之一[8]。地形起伏度是表示某一确定区域中最高海拔和最低海拔之差[9]，它是描述区域地形特征的一个宏观性指标，用以表征地面的起伏状况和切割程度，被广泛应用于自然地质灾害等定量评价方面[10-14]，目前，结合地形起伏度进行有机质空间规律的研究还相对较少。

本试验以黄土丘陵区为研究区，选取地形起伏度和地貌因子进行地形分区，然后进行Kriging 插值，并将其与直接插值进行比较，对比2 种方法的预测精度，旨在提出一种更适合丘陵山区土壤有机质的插值预测方法，为获取更精准的土壤有机质空间分布提供指导性建议。

1 材料和方法

1.1 研究区域与数据来源

1.1.1 研究区概况 试验以晋中市太谷区为研究区，该区位于山西省中部，地处晋中盆地东北部（东经112°28′～113°01′，北纬37°12′～37°03′），隶属于黄土高原，地形复杂多样，主要有平原、丘陵和山地，由东南向北倾斜，海拔高度为763～1 900 m；土地利用类型主要为耕地、园地、林地和草地（图1-A）。该区总体格局为西北低东南高，平原与丘陵交错分布；全区耕地面积为28 885.46 hm2，空间分布比较明显，主要分布在763～933 m 的海拔范围内（图1-B）；成土母质主要为黄土状物质、河流冲积物、马兰黄土等，土壤类型为褐土和潮土。

1.1.2 数据来源 本研究所需数据主要包括分辨率为30 m 的SRTMDEM数据，来源于中国科学院计算机网络信息中心地理空间数据云网站（www.gscloud.cn）；土壤有机质数据，来源于山西省2010 年测土配方项目采样；耕地数据，来源于2015 年1∶10000 太谷区土地利用变更调查数据库以及2017 年太谷区耕地质量等级更新成果和山西地貌。

1.2 研究方法

1.2.1 地形分区

1.2.1.1 地形起伏度的提取 使用Arcgis 矩形窗口大小为n×n 像元（n＝2，3，…，23）提取地形起伏度：一统计n×n（n＝2，3，…，23）不同窗口内像元的最大值和最小值；二计算不同窗口内最大值与最小值之间的差值；三统计各窗口下的平均起伏度值。

1.2.1.2 最佳地形起伏单元的计算 均值变点分析法检验最有效的是恰有一个变点[15]，已经被广泛应用于提取地形起伏度最佳统计单元。根据原理构建样本序列[16]。具体过程为：首先计算不同窗口下单位面积上的地势大小序列T（单位地势梯度）（Ti＝平均起伏度（ti）/邻域面积（si）检验最有效，然后对序列T 取对数lnT，得到序列X（{xi，i＝2，3，4，…，23}））；利用公式（1）计算样本序列X 的算数平均值，利用公式（2）和公式（3）分别计算样本序列X 的统计量S 和Si的值。

1.2.1.3 划分地形 根据数字地貌制图规范，地形起伏度可分为7 级，即平原（＜30 m）、台地（30～70 m）、丘陵（70～200 m）、小起伏山地（200～500 m）、中起伏山地（500～1 000 m）、大起伏山地（1 000～2 500 m）和极大起伏山地（＞2 500 m）[17]。山西地貌有平原、山地、台地、丘陵、河漫滩五大一级类型。结合地形起伏度和地貌类型进行地形分区。

1.2.2 Kriging 空间插值方法 Kriging 插值法是基于空间自相关性和二阶平稳假设，依据估算误差最小和半方差函数分析，赋予一定邻域内样点不同权重后，计算样点值加权和即为插值结果。

式中，γ（h）为距离h 的样点对的半方差；h 为2 个样点之间的距离；N（h）表示样点对距离为h 所有样点对应的个数；z（xi）和z（xi＋h）分别是采样点有机质在空间位置xi和xi＋h 处的实测值。当γ（h）不与方向变化有关、只依赖于距离h 时，则称γ（h）各向同性。

在数据量很大时需要在拟合变异函数之前进行分组操作，这样才可以任意距离下的变异函数进行后续插值。球状模型、指数模型、高斯模型、线性模型作为传统理论拟合模型应用比较广泛，以下是对普通Kriging 插值原理进行的说明。

Kriging 插值预测结果的精确性是满足无偏性和估计方差最小。

公式（5）和（6）经推导，用变异函数来表示如下：

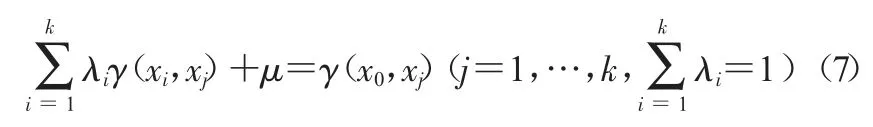
式中，k 为总的采样点数；λi为克里金权重系数，表示每个采样点xi处的有机质含量对预测点x0的影响范围；μ 为克里金拉格朗日乘子；γ（xi，xj）变异函数值是表示实际采样点在空间距离xi和xj之间的变异值；γ（x0，xj）表示预测点x0与采样点xj之间距离的变异值。

式中，z*（x0）表示预测点x0处的值；x1，…，xk为已知样本的实际位置；z（x1），…，z（xk）为对应的样本有机质实际含量。

1.2.3 预测结果准确性检验 本研究是通过回归系数r 来验证采样点位置处的预测精度，以及Isaaks 和Shrivastava 定义的平均预测误差（ME）、平均标准误差（ASE）、标准化均方根误差（RMSSE）、均方根误差（RMSE）[18]4 个验证指标。其中，回归系数r 值的大小是衡量变量之间的密切程度；均方根误差RMSE 是观测值与真实值偏差的平方和与观测次数的比值的平方根来计算得到的。实际测量中，由于观测样点次数有限，所以用最接近的值来代替实际值。在一组数据中由于特殊值造成的误差影响，会对标准误差造成影响，所以预测精度用标准误差来衡量。

2 结果与分析

2.1 邻域分析与均值变点分析

利用Arcgis 对研究区在窗口大小分别为2，3，…，23 的情况下提取地形起伏度，窗口大小与平均起伏度的关系如表1 所示。

由表1 可知，平均起伏度值随邻域面积的增大逐渐增大，但当邻域面积达到一定的阈值时，其变化趋势逐渐平缓。

平均起伏度和领域面积关系曲线符合逻辑斯蒂规律[16]。从图2 可以看出，经过统计学检验，拟合度满意，拟合方程为y＝20.171lnx＋14.056，拟合系数R2＝0.966 5，平均起伏度与邻域面积成正比关系，趋势由陡变缓处即为最佳统计单元面积。

S 和Si通过均值变点分析法计算得出，利用SPSS 统计软件做出S 和Si差值的变化曲线如图3所示。从图3 可以看出，在第8 个点时S 和Si差值达到最大，该点是曲线由陡变缓的那一点，符合均值变点分析法的要求。由此通过邻域分析法和均值变点分析计算得出，基于30 m 分辨率的dem 数据提取晋中市太谷区地形起伏度的最佳统计为9×9。

2.2 地形分区结果

本研究的最佳统计单元为9×9，在该窗口下该区域的地形起伏度范围为0～241 m，按照数字地貌制图规范[17]，该研究区耕地按地形起伏度可划分为0～30 m 和30～70 m（图4-A）。晋中市太谷区地貌类型为平原、台地、丘陵、山地（图4-B）。将地形起伏度分级结果与地貌类型进行叠加分析，可分为0～30 m 的平原、台地、丘陵、山区，30～70 m的平原、台地、丘陵、山区共8 个区。

2.3 土壤有机质统计分析

研究区土壤有机质采样点描述性统计如表2所示，利用SPSS 进行分析检验显示，土壤有机质含量符合正态分布规律。不同地形起伏度下地貌类型的土壤有机质含量差别较大，符合Kriging 插值的条件；而且由于差异性也为接下来进行半方差函数结构建模以及依据地形分区插值提供依据。

表2 土壤有机质含量描述性统计结果

由表3 可知，不同地形起伏度的地貌类型土壤有机质含量的平均值、变异系数各不相同，从另一个角度证明了将地形起伏度和地貌类型作为辅助变量进行分区Kriging 插值法的可行性。

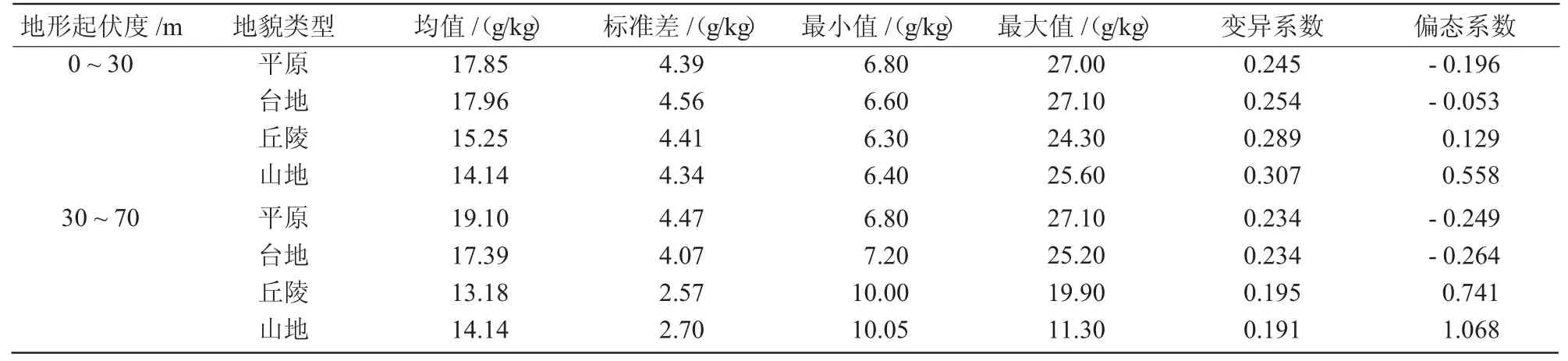
表3 分区土壤有机质含量描述性统计结果

2.4 地统计空间分析及Kriging 空间插值

利用地统计软件GS+对各分区采样点土壤有机质含量进行半方差函数及拟合参数计算[19-21]，其结果如表4 所示。

根据最优拟合模型决定系数大、残差小为依据，比较各模型参数，选择最优拟合指数参数[22]。根据块金值的相关定义，原理上采样点之间距离等于0 时，半变异函数值也是0，但由于存在测量误差以及空间变异特征的影响，土壤样点十分相近时，半变异函数值会发生变化，从而引起块金值效应，而且可以反映最小距离尺度下变量的变异特征及误差。由表4 可知，不同地形起伏度和不同地貌类型下土壤有机质与不分区有机质的块金值不同，说明土壤有机质的空间异质性较大，分区与整体插值土壤有机质空间变异不同。

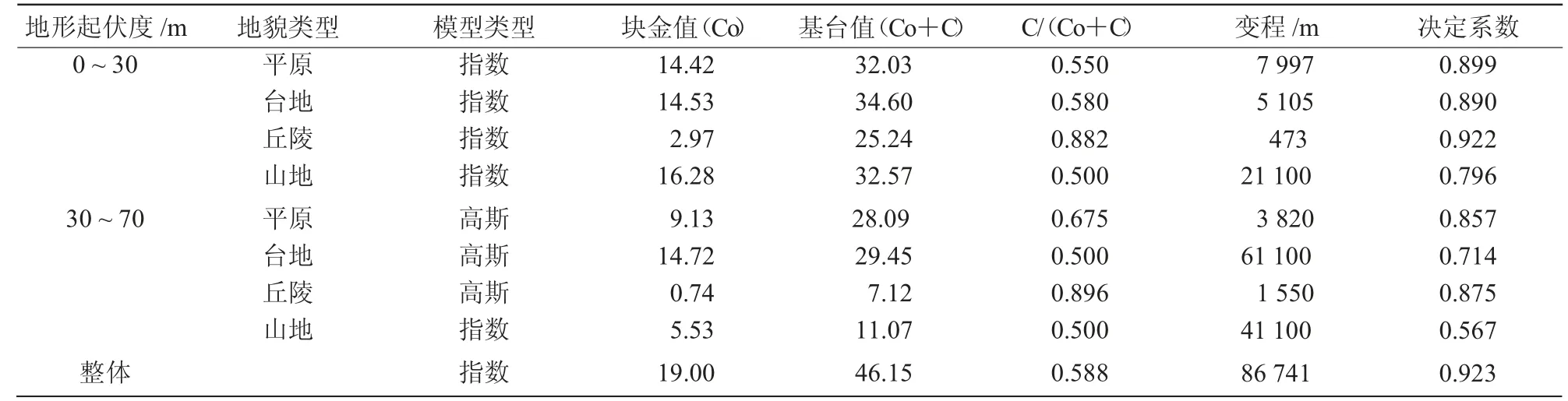
表4 土壤有机质含量的半方差函数模型和参数

由于该区域气候差别很小，各分区的土壤有机质结构方差C 不同，所以该区域的空间变异特征主要是由地形因素造成的。C/（Co＋C）即空间相关度，是块金值与基台值的比值，该值反映了系统变量的空间相关性的大小。根据CAMBARDELLA 等于1994 年提出的划分依据，块金基台比小于25%时，表明空间相关性强，大于75%则空间相关性较弱，处于二者之间，说明具有中等强度的空间相关性。由表4 可知，在地形起伏度不同地貌类型土壤有机质的C/（Co＋C）处于25%～75%时，表明土壤有机质呈现中等强度的空间相关性。不同地形起伏度山地的C/（Co＋C）都为0.500，小于平原、台地和丘陵地区，说明山地上的耕地土壤有机质受地形起伏度的影响更大。各分区的模型总体拟合效果较好，决定系数除地形起伏度为30～70 m 的山地之外都在0.72 以上，这与山地上的耕地少采样点少有很大关系。地形分区下山地的变程相对较大，与晋中市太谷区山地地形地貌空间结构相吻合。

与原始有机质含量相比，不同地形起伏度下，平原、台地、丘陵、山地的块金值、基台值都降低，丘陵的块金基台比升高，说明不同分区土壤有机质的变化比较小，相对比较均匀，表明该区域土壤有机质含量进行预测时考虑地形的合理性，把地形起伏度和地貌作为辅助变量对该研究区土壤有机质含量预测的精度较好。

2.5 预测精度对比分析

由2 种方法所得到的实测值与预测值的散点分布图和线性回归方程如图5 所示，以地形起伏度和地貌类型为辅助变量进行分区的Kriging 插值得到的实测值与预测值的决定系数（0.463 4）明显高于普通的Kriging 插值法得到的（0.261 5）。

ME 越接近0 越满足预测的无偏性；RMSSE 越接近1 说明预测标准误差越准确；RMSE 和ASE 尽可能小，预测值与实测值的差值更小，使结果更精确[23-25]。从表5 可以看出，地形起伏度在0～30 m 山地的无偏性最好；在30～70 m 的丘陵和山地预测值与实测值的偏差最小，所以结果更准确。各分区土壤有机质的交叉验证均满足上述条件[26]。

2.6 土壤有机质的空间分布特征

通过普通Kriging 和分区Kriging 这2 种方法预测得到的土壤有机质空间分布如图6 所示，分区Kriging 插值结果空间分布特征及空间递变规律更加明显，普通Kriging 插值得到的土壤有机质含量范围为11.47～22.41 g/kg，而分区Kriging 插值得到的土壤有机质含量为7.38～25.95 g/kg。总体上看，研究区2 种方法估计的土壤有机质空间分布格局基本一致，都表现为西北部的土壤有机质含量较高，东南部较低。

从2 种预测结果局部分布特征看，土壤有机质含量差异还是比较明显，分析发现，普通Kriging 插值，由于平滑效应使不同地形起伏度地貌类型的有机质含量差异变低[27-28]，插值结果不能精确反映出局部信息，例如，山地、丘陵上耕地由于个别采样点的土壤有机质含量偏高，造成该区域的插值结果偏高，而且分布规律连续规整，因此无法体现出太谷区的局部信息；并且普通Kriging 插值并没有对采样点根据地形归类，相邻距离近的点忽略了空间位置因素造成的误差，且普通插值法忽略了土壤有机质空间平稳过渡，造成预测的土壤有机质分布特征不明显。但分区Kriging 是按照地形分区对采样点进行归类，可以有效消除邻近点插值误差，更能反应土壤有机质的空间特点以及研究区域局部分布情况，更适合用于分析不同因素与土壤有机质空间规律之间的关系。

3 结论

本研究结果表明，结合地形起伏度和地貌类型进行分区Kriging 插值法得到的研究区土壤有机质含量的范围为7.38～25.95 g/kg，而直接Kriging 插值法得到的研究区土壤有机质含量范围为11.47～22.41 g/kg，2 种方法所得范围大致一致，但分区Kriging 插值法预测精度更高。这是因为研究区地貌和地形起伏度不同，导致区域内土壤有机质含量不同，结合地形起伏度和地貌进行分区以及对采样点进行归类可以消除邻近采样点对其空间插值预测精度的影响，从而提高其预测精度。基于地形分区的Kriging 插值法对丘陵和山地的预测结果更好，因此，对于研究地形复杂山区的有机质空间变异规律，可以考虑借助辅助变量对空间规律进行精细研究。