排球大力跳发中的马格努斯效应
2021-02-24司友志金稳
司友志 金稳










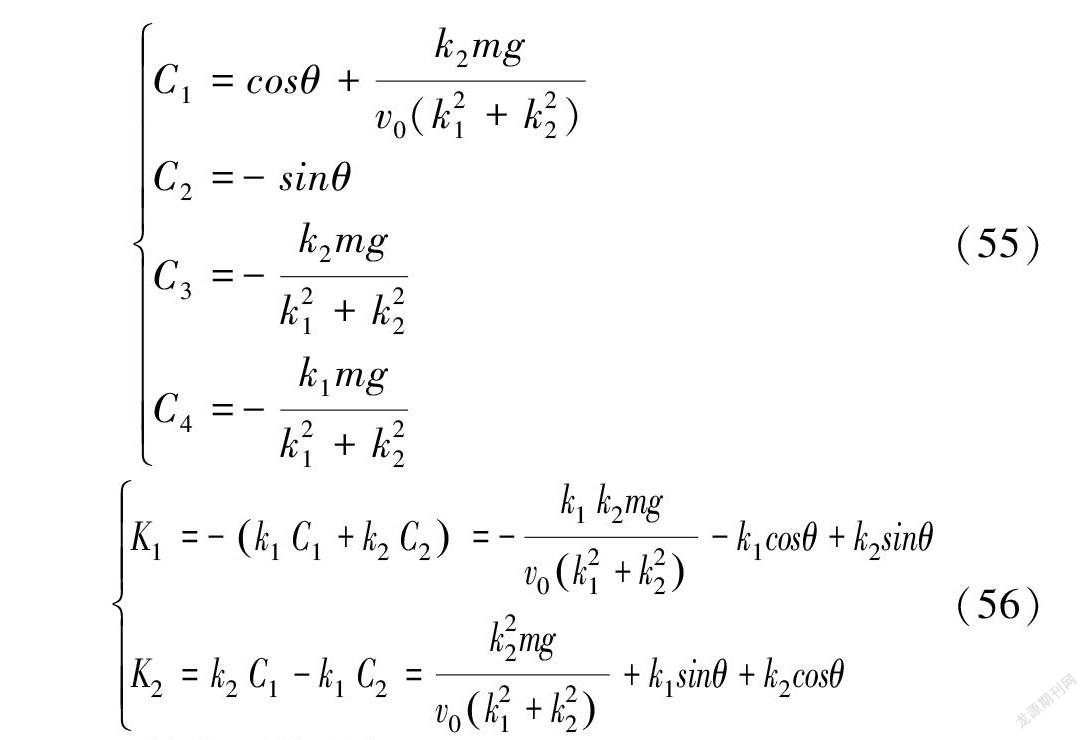

摘 要:当球体在空气中高速旋转时,由于马格努斯效应,球体会受到横向的马格努斯力的作用,其运动轨迹会发生弯曲而偏离正常的抛物线的现象。通过对球类运动项目中马格努斯效应产生的原理进行分析、推理和研究,建立了三个球体运动模型:一是不考虑空气阻力和马格努斯力,只受重力影响的理想模型;二是不考虑旋转,即没有马格努斯力,但是考虑空气阻力的较为实际的球体运动模型;三是在第二种模型的基础上再加上球体上旋引起的马格努斯力的影响,并对三个模型都做了一定的数学分析计算,得到了每个模型在水平x方向和竖直y方向的速度v和位移随时间的关系表达式,从动力学方程出发,综合考虑空气对球体运动的阻力作用和马格努斯效应,对空中同时做平动和转动的球体做受力分析,从而研究得到跳发上旋球时排球运动的弧线方程,进而可以算出偏移量。根据理论计算结果,我们可以结合实际情形,给出具有针对性的排球的教学和训练指导,以加强训练效果,提高专项运动技术水平。
关键词:马格努斯效应;伯努利定律;球速;旋转速度;运动轨迹方程;偏移量;排球
中图分类号:G804.63 文献标识码:A 文章编号:1009-9840(2021)06-0057-07
Magnus effect of volleyball smashing jump service
SI Youzhi, JIN Wen
(University of Science and Technology of China, Hefei 230026, Anhui, China)
Abstract:When the ball rotates at high speed in the air, due to the Magnus effect, the ball will be affected by the transverse Magnus force, and its trajectory will bend and deviate from the normal parabola. Based on the analysis, reasoning and research of the principle of Magnus effect in ball games, this paper establishes three ball motion models: one is the ideal model which is only affected by gravity without considering air resistance and Magnus force; the other is the more practical ball motion model which does not consider rotation, that is, without Magnus force, but considering air resistance; the third is the more practical ball motion model in the third part On the basis of the two models and the influence of Magnus force caused by the upward rotation of the sphere, the mathematical analysis and calculation of the three models are carried out, and the expressions of the relationship between the velocity V and displacement of each model in the horizontal X direction and vertical Y direction with time are obtained. Starting from the dynamic method, the resistance effect of the air on the sphere motion and the Magnus effect are comprehensively considered At the same time do translation and rotation of the ball to do force analysis, so as to get the arc equation of volleyball movement when jump serve topspin ball, and then can calculate the offset. According to the results of theoretical calculation, we can combine with the actual situation, give targeted volleyball teaching and training guidance, in order to strengthen the training effect and improve the technical level of special sports.
Key words:Magnus effect; Bernoulli's law; ball speed; rotational speed; motion trajectory equation; offset;volleyball
收稿日期:2021-05-08
作者簡介:司友志(1981- ),男,安徽宣城人,硕士,副教授,研究方向体育教育。
在当代排球比赛中,发球是唯一不受他人干扰,完全由自主完成的环节,也是队伍发起的第一波进攻。发球的好坏可谓在很大程度上影响着比赛的输赢。当代发球主要有两种方式:一是大力跳发,二是发飘球。大力跳发由于其无与伦比的冲击性、破坏性和观赏性,越来越受到观众的认可,逐渐成为世界一流排球运动员的首选发球方式。特别是在世界男子排球比赛中,经常可以欣赏到高质量的大力跳发球,像意大利男排接应伊万·扎伊采夫,古巴男排主攻维尔福来多·莱昂,中国男排接应江川等队员的跳发球都十分出彩。
跳发球的优势具体表现在哪些方面呢?简单来说有四点。第一,球本身速度特别快,经常可以达到120 km/h甚至130 km/h以上,而飘球速度通常只有60~70 km/h,故大力跳发留给接球队员的反应时间相对来说短很多。第二,球速快带来的冲击力也特别大,很多队员在取准位置后也难以接好。第三,更重要的,跳发球通常伴随着强烈的旋转,马格努斯效应比较明显,球在空中相对于没有旋转情况下的正常轨迹有着较大的偏移量,如上旋球会有较强烈的“急坠”现象,再加上较短的反应时间,给接球队员带来相当大的麻烦,因而大力跳发经常能够破坏对手一传导致不到位甚至直接得分。第四,就是大力跳發球的观赏性远比发飘球的观赏性要好。
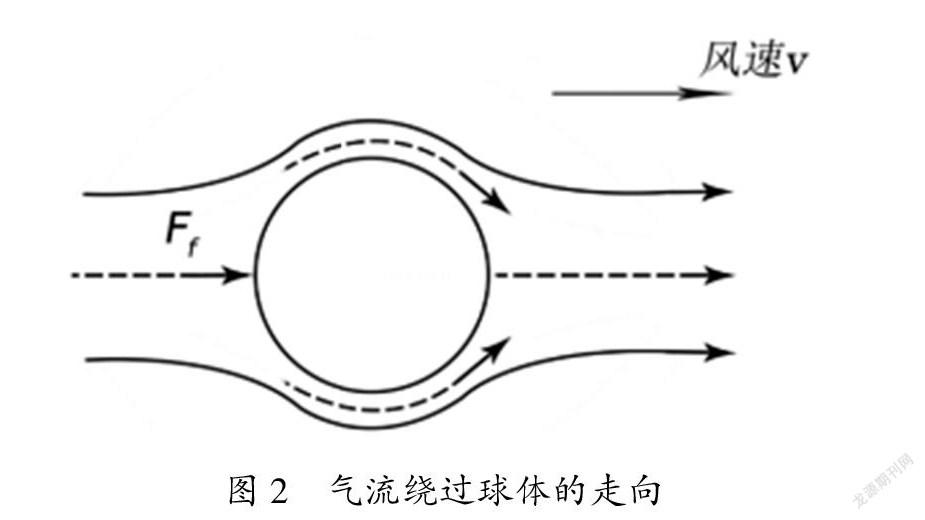
什么是马格努斯效应?简单解释是,一个旋转的球在它周围带动一些空气一起旋转,在它周围产生一种旋转空气的漩涡。这种循环空气减慢了一侧通过球的空气流动,同时又使另一侧的空气加速。根据伯努利的原理,在速度较大的一侧压力较低,在空气速度较小的一侧压力较高。由此产生的压力不平衡导致垂直于球的旋转轴及其速度作用的力,导致球的偏转。
当然并不是排球运动才受到马格努斯效应的影响,很多球类运动都受到其影响。比如足球里面有名的“香蕉球”,乒乓球的“弧圈球”,棒球、高尔夫球的拐弯球等。一直以来,部分研究人员对这一类现象用马格努斯效应和伯努利定律进行了定性分析,偶尔也进行过动力学运动学的定量分析,如部分研究者分别对足球、网球、棒球做了相关运动的研究,潘慧炬也曾经用女排发侧旋球的例子进行了大致计算,但是当时的研究并未考虑到重力的影响,有所疏漏。特别对排球上旋球的研究相对较少,怎样利用马格努斯效应和伯努利定律更有效地指导运动员发出威胁更大的跳发球,让对手防不胜防,从而达到破坏对手方一传甚至直接得分的目的,这方面的研究就更少。因此,研究马格努斯效应在排球等球类运动项目中的影响,对于相关球类运动项目的教学和训练有着重要的指导意义和实践意义。
1 研究方法
1.1 文献资料法:查阅排球书籍并从知网和中国学术期刊网检索排球发球相关文献,对排球大力发球技术进行理论梳理,为后期研究做好理论基础。
1.2 数理统计法:对世界一流排球运动员大力发球数据进行统计,为研究提供数据支撑。
2 各种条件下的排球运动规律
任何在空中行进的旋转球都经历至少四种力:重力、气动阻力、浮力和马格努斯力。但是在用排球、足球等作为研究对象时,浮力相对于其他力来说是微小的,可以被舍去。
2.1 基本模型——只受重力时的运动规律
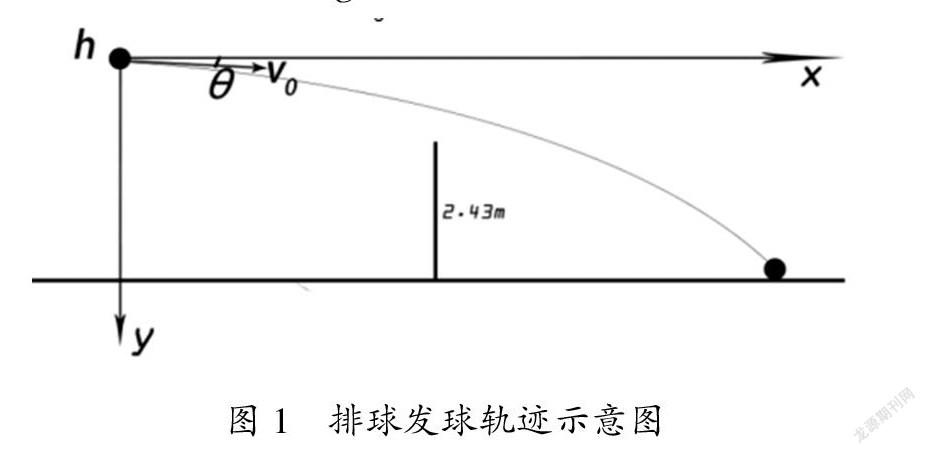
由简单的高中物理知识,我们知道,当物体在空中只受重力而不考虑其他力的作用时,其运动轨迹应该是一条抛物线的一部分,具体由其初始条件决定。假设初速度为v0,击球高度为h,初速度与水平面得夹角为θ,则有:
x:x=v0cosθ·t(1)
y:y=v0sinθ·t+12gt2(2)
式(2)中,令y=h,则可以求得发球时间为:
t=-v0sinθ+ v20sin2θ+2ghg(3)
整理可以得到不含时间t的只有横纵坐标xy的关系即运动学方程式:
y=sinθcosθx+g2v20cos2θx2=v202sinθcosθ2v20cos2θx+g2v20cos2θx2
=12v20cos2θ(gx2+v20sin2θ-x)
如果取y=h,解方程则可以得到发球距离:
L=-v20sin2θ+v0 v20sin22θ+8ghcos2θ2g(4)
这是最理想的发球距离,可以得到最佳马格努斯力和空气动力,获得最佳发球效果。实际发球过程中可根据不同发球距离考虑不同空气阻力和马格努斯力的影响。
2.2 阻力模型——空气阻力对排球运动的影响
任何物体在空气中运动都会受到空气阻力的影响,空气阻力的大小与物体截面积、相对运动速度、空气粘滞系数等有关。
球体在空气中以速度v运动,也可以由相对运动原理等效看成是空气以速度v吹向静止的球,球体受到的空气阻力也就等效成运动的空气对球的推力。
当球体速度不是很大时,其受到的空气阻力大小可以表示为:
Ff=12Cdρv2A=kv2(5)
k=CDρA2=CDρ2·14πd2=CDρπd28(6)
其中,A是球体截面积,d是球体直径,排球取d=0.21m;ρ是流体密度,常温下空气密度值为ρ=0.129 kg·m-3。CD是阻力系数。
实验证明,绕流球体的阻力系数CD随着绕流雷诺数Re的增加而减小。图3绘出了粘性流体绕圆球流动的阻力系数CD随Re数变化的实验曲线,其临界雷诺数Re=(2~3)×105。对应于图3各区域的CD近似计算公式有:
CD=24Re,(Re<1,斯托克斯公式)
CD=24Re1+316Re,1≤Re<5,奥森公式
CD=24Re1+316Re12,5≤Re<100,奥森修正公式
CD=13Re,10<Re<1000,阿连公式
CD=0.44,500<Re<2-105,牛顿公式(7)
对于雷诺数,有
Re=ρvdμ(8)
μ是空气粘度系数,常温下其值约为1.85·105Pa·s。假设发球速度为v=120 km·h-1=33.3 m·s-1,则计算可得跳发球时排球在空气中的雷诺数为
Re=48 762
所以可取CD=0.44,则可计算得到
k=9.83×10-4 kg·m-1。(9)
下面来求解其轨迹方程。根据受力分析可以列出动力学方程:
x:kv2cosα=-mdvxdt(10)
y:-mg+kv2sinα=mdvydt(11)
v=vx+vy
其中,α是某一时刻排球速度方向与水平的夹角大小。
在求解这个微分方程时,由于变量v是二次,故方程得不到解析解。为了求得解析解,我们用一个等效k1,使其满足:
Ff=kv2=k1v
即有
k1=kv
这样将方程降次,便能得到解析解。但是速度v并不是一个常数,而是随时间t变化的。然而在我们研究的过程内,初速度較大,持续时间短,重力会使得球体加速,空气阻力使其减速,二者近似平衡,即我们认为这短时间内速度基本不变。故有:
k1=kv0(12)
方程(9)(10)转化为:
x:-k1vcosα=mdvxdt(10′)
y:mg-k1vsinα=mdvydt(11′)
又因为有:
vcosα=vx,vsinα=vy
方程化成:
x:k1vx=-mdvxdt(10″)
y:mg-k1vy=mdvydt(11″)
可以分别解得水平竖直方向上的速度随时间的变化关系:
x:vxt=v0cosθe-k1mt(13)
y:vyt=v0sinθ-mgk1e-k1mt+mgk1(14)
两个方向上速度分别对时间积分,进而可以得到两个方向上位移随时间的变化关系:
x:xt=mv0cosθk11-e-k1mt(15)
y:yt=mk1v0sinθ-mgk11-e-k1mt+mgk1t(16)
同样,当y=h时,我们可以得到球体在空中的运动时间的数值解,再带入x(t),则可以计算出发球距离。
2.3 旋转模型——考虑空气阻力和马格努斯力的排球运动规律
当球体在空气中的移动速度为v,自转角速度为ω时,其受到的马格努斯力的大小为:
FM=18πρd3ωv=k2v(17)
k2=18πρd3ω=18π×0.129×0.213ω=4.69×10-4ω
其中,ρ为空气密度,d为排球直径。
其实在球体运动过程中,ω也会随着时间变化,准确地应该写成ω(t)。但是球体运动时受到切向阻力应该远远小于法向阻力,即旋转速度ω变化不大,我们直接认为其是一个定值,由初始条件决定。
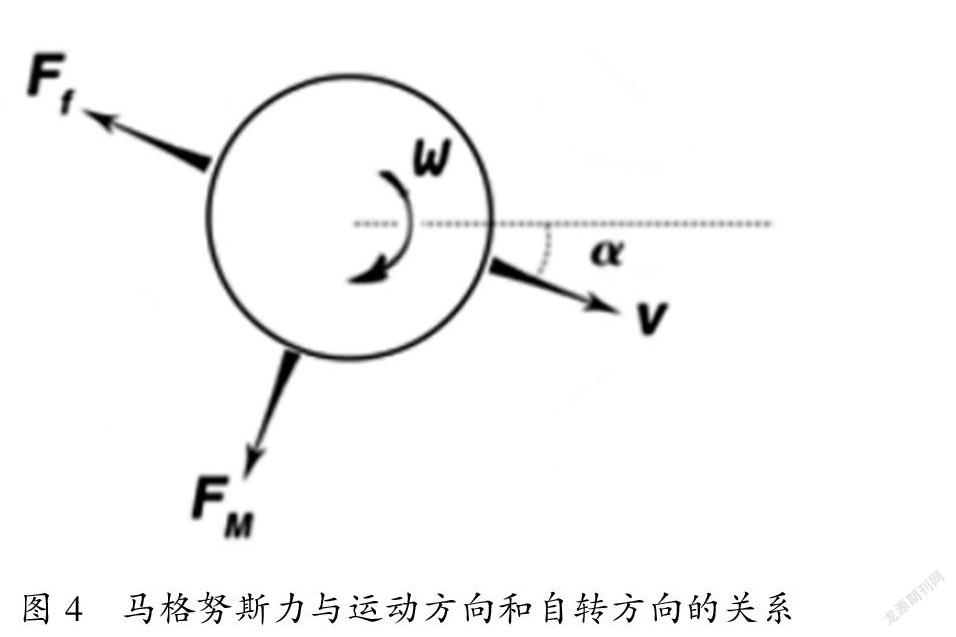
马格努斯力的方向是ω×v的方向,满足右手螺旋定则,即右手四个指头与大拇指垂直,四指从ω的方向卷向v的方向,此时大拇指的方向即是马格努斯力的方向,垂直于速度方向。侧向受力是基本均衡的,两个力相反,并相互抵消。简单来说,如果我们发的是一个水平的上旋球,则马格努斯力的方向刚好是竖直向下的。
加上马格努斯力后球体运动的动力学微分方程变为:
Ff+FM=-mdvdt
两个方向的分量为:
x:-kv2cosα-k2vsinα=mdvxdt(18)
y:mg-kv2sinα+k2vcosα=mdvydt(19)
同样,这个方程无法求得解析解,我们用跟上面一样的等效的一次形式的空气阻力方程对方程进行简化:
x:-k1vcosα-k2vsinα=mdvxdt(18′)
y:mg-k1vsinα+k2vcosα=mdvydt(19′)
再利用:
vcosα=vx,vsinα=vy
方程最终转化成:
x:-k1vx-k2vy=mdvxdt(18″)
y:mg-k1vy+k2vx=mdvydt(19″)
下面我们需要来求解这组方程。首先由(18″)式可得:
vy=-mk2dvxdt-k1k2vx(20)
带入到(19″)中,有
d2vxdt2+2k1mdvxdt+k21+k22m2vx=-k2gm(21)
其特征根方程为:
r2+2k1mr+k21+k22m2=0(22)
特征根为:
r1,2=-k1m±k2mi(23)
故方程的解的形式为:
vxt=v0e-k1tmC1cosk2tm+C2sink2tm+C3(24)
根据初始条件:
vx0=v0cosθ=v0C1+C3
mv'x0=-k1v0cosθ-k2v0sinθ=-k1vx(0)+k2v0C2
及方程(21)可以解得几个未知常数分别为:
C1=cosθ+k2mgv0(k21+k22)
C2=-sinθ
C3=-k2mgk21+k22(25)
故vx表示为:
vxt=v0e-k1mtcosθ+k2mgv0k21+k22cosk2mt-sinθsink2mt-k2mgk21+k22(26)
再将方程(23)带入到方程(24)中,可以解得vy的通解为:
vy1t=v0e-k1mtcosθ+k2mgv0k21+k22sink2mt+sinθcosk2mt+k1mgk21+k22(27)
我们设vyt的特解为vy2(t)。则vy表示为:
vyt=vy1t+vy2(t)(28)
将(28)带入到(19″)有:
mg-k1(vy1+vy2)+k2vx=md(vy1+vy2)dt(29)
而vy的通解应该也满足(19″)式,即
mg-k1vy1+k2vx=mdvy1dt(30)
则特解vy2(t)应该满足的条件为:
-k1vy2=mdvy2dt(31)
解得:
vy2t=C4e-k1mt(32)
则vy的解为:
vyt=v0e-k1mtcosθ+k2mgv0k21+k22sink2mt+sinθcosk2mt+k1mgk21+k22+C4e-k1mt
根据初始条件,当t=0时,
vy0=v0sinθ=v0sinθ+k1mgk21+k22+C4
得到:
C4=-k1mgk21+k22(33)
则有:
vyt=v0e-k1mtcosθ+k2mgv0k21+k22sink2mt+sinθcosk2mt+k1mgk21+k22(1-e-k1mt)(34)
进一步分别对时间积分可以得到两个方向的位移-时间关系:
x:xt=mv0k21+k22[e-k1mt(K1cosk2mt+K2sink2mt)-K1]+C3t(35)
y:yt=mv0k21+k22[e-k1mt(K1sink2mt-K2cosk2mt)+K2]-C4t-mk11-e-k1mt(36)
其中,常数项K1,K2分别为:
K1=k1C1+k2C2=k1k2mgv0(k21+k22)+k1cosθ-k2sinθK2=k2C1-k1C2=k22mgv0k21+k22+k1sinθ+k2cosθ(37)
可见两个运动水平竖直两个方向的位移随时间的表达式的形式相对比较复杂,含有较多常数项。
3 分析与讨论
上文我们主要建立了三个球体运动模型:一是不考虑空气阻力和马格努斯力,只受重力影响的理想模型;二是不考虑旋转,即没有马格努斯力,但是考虑空气阻力的较为实际的球体运动模型;三是在第二种模型的基础上再加上球体上旋引起的马格努斯力的影响,并对三个模型都做了一定的数学分析计算,得到了每个模型在水平x方向和竖直y方向的速度v和位移随时间的关系表达式。下面我们将采用画图和实际数值的方法对这几个模型做进一步的分析对比。
为了方便讨论对比,我们先列出用得到的常数值:
空气密度:ρ=0.129 kg·m-3
排球直径:d=0.21 m
排球质量:m=0.27 kg
重力加速度:g=9.80 m·s-2
3.1 準确模型
这儿说的准确是指,阻力式准确来说是与速度的二次方程正比。但在上面的计算中,由于求解微分方程时得不到解析解,故用一个等效的一次式做了近似,从而得到的是等效模型式。而准确模型得相关方程为:
3.1.1 基本模型
x:x=v0cosθ-t(38)
y:y=v0sinθ-t+12gt2(39)
3.1.2 阻力模型
x:kv2cosα=-mdvxdt(40)
y:-mg+kv2sinα=mdvydt(41)
k=CDρπd28=9.83×10-4kg·s-1(42)
3.1.3 旋转模型
x:-kv2cosα-k2vsinα=mdvxdt(43)
y:mg-kv2sinα+k2vcosα=mdvydt(44)
k2=18πρd3ω=7.04×10-3kg·s-1(45)
由准确的二次阻力公式推出来的阻力模型和旋转模型方程,我们都没有办法得到解析解,也没有简单的办法可以直接得到数值解,在以后有了更方便的工具后可以对其进行数值图像研究。我们此次不做太多讨论。
3.2 等效模型
为了简化模型求得解析解,我们提出了阻力的一次等效公式:
Ff=kv2=k1v
并认为
k1=kv0(46)
所得到两种模型的方程为:
3.2.1 阻力模型
速度-时间关系:
x:vxt=v0cosθe-k1mt(47)
y:vyt=v0sinθ-mgk1e-k1mt+mgk1(48)
位移-时间关系:
x:xt=mv0cosθk11-e-k1mt(49)
y:yt=mk1v0sinθ-mgk11-e-k1mt+mgk1t(50)
3.2.2 旋转模型
速度-时间关系:
x:vxt=v0e-k1mtcosθ+k2mgv0k21+k22cosk2mt-sinθsink2mt-k2mgk21+k22(51)
y:vyt=v0e-k1mtcosθ+k2mgv0k21+k22sink2mt+sinθcosk2mt
+k1mgk21+k221-e-k1mt(52)
位移-时间关系:
x:xt=mv0k21+k22[e-k1mt(K1cosk2mt+K2sink2mt)-K1]+C3t(53)
y:yt=mv0k21+k22[e-k1mt(K1sink2mt-K2cosk2mt)+K2]-C4t-mk11-e-k1mt(54)
其中,各常数项分别为:
C1=cosθ+k2mgv0(k21+k22)C2=-sinθC3=-k2mgk21+k22C4=-k1mgk21+k22(55)
K1=-k1C1+k2C2=-k1k2mgv0k21+k22-k1cosθ+k2sinθK2=k2C1-k1C2=k22mgv0k21+k22+k1sinθ+k2cosθ(56)
3.3 数值图像分析
从方程来看,模型越复杂得到的公式自然也就更加复杂。阻力模型所得到的结果应该是最接近我们平时发的没有旋转的不具有太强攻击性的一般球的实际轨迹,而加上旋转以后的影响便可以从旋转模型里面看出来。为了更加直观地看出阻力、旋转带来的影响,我们可以分别从数值和图像两个方面去讨论。我们先假定一组初始条件:
初速度:v0=120 km·h-1=33.3 m·s-1;
方向夹角:θ=3.00;
发球高度:h=3.40 m;
旋转速度:ω=15.0 r·s-1;
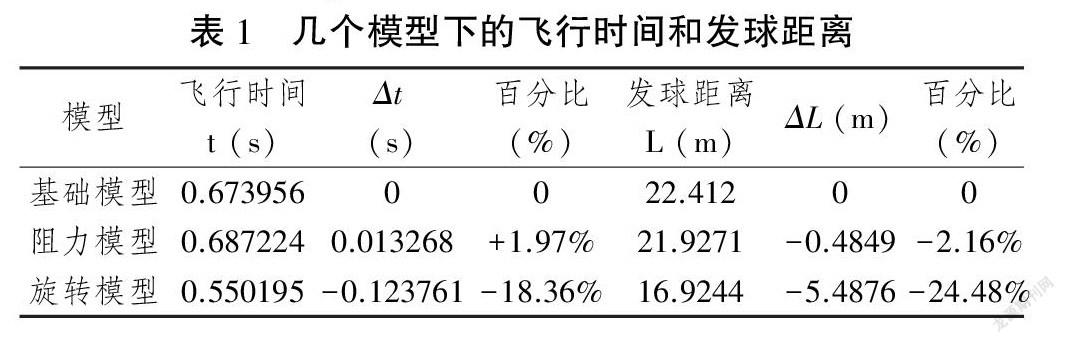
通过相应的公式,利用电脑,可以计算得到各种情形下的发球距离,如表1:
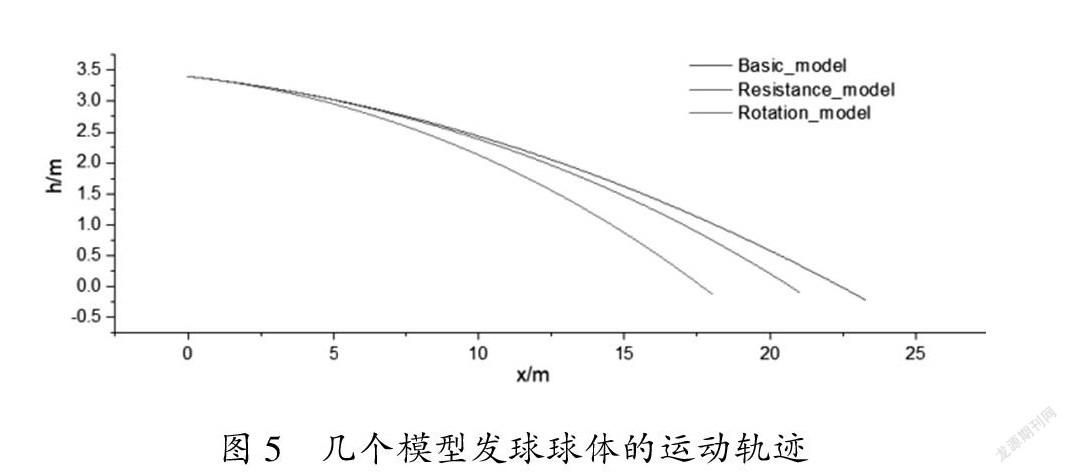
由表1中信息,由于空气阻力的存在,球体在空中飞行时间会延长,发球距离会缩短,但是这两个变化量都是比较小的,只约基础模型的1%~2%。而加上旋转比不加旋转时,球的飞行时间从0.673 956 s变为0.550 195 s,减少0.123 761 s,约18.36%,留给防守方判断的时间明显缩短,再加上本来飞行时间就极短,故对接球一方的队员的反应能力来说是一个极大的考验;发球距离从22.412 m减少至16.924 4 m,减少5.4876 m,这是一个非常可观的变化量,即有着非常明显的“急坠”现象。这个变化会给接球一方进一步带来很大的难度,而且使得球更容易落在界内不致于出界丢分。我们知道,排球场的长度是18 m,从表1中数据可以看见,如果不加旋转,按我们假设的初始条件计算,会使得球直接飞出界外;而加上旋转后由于明显的距离缩短,则可以落在界内。图5是根据上述初始条件得到的几个模型下球体的运动轨迹。
上述假设的条件是根据世界一流排球运动员的数据得出的,下面我们用与我们平时情况更加接近的一组初始条件进行计算对比:
初速度:v0=72 km·h-1=20.0 m·s-1;
方向夹角:θ=-10.0°;
发球高度:h=2.30 m;
旋转速度:ω从0 r·s-1到12r·s-1变化。
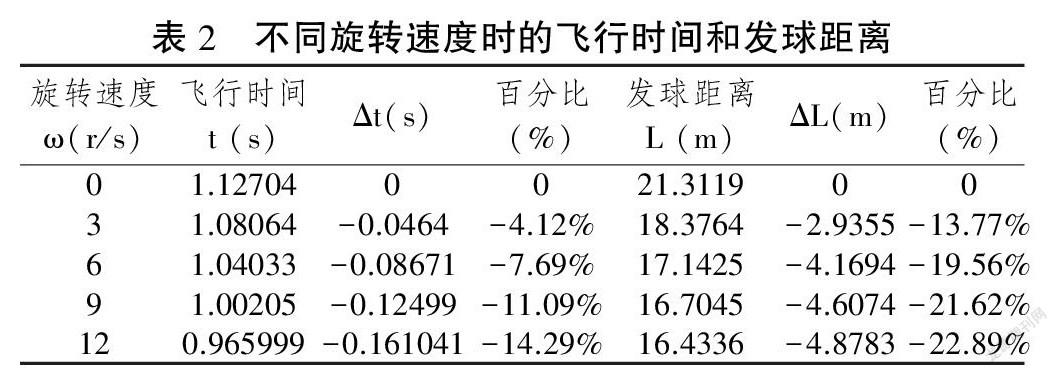
根据以上数据,我们可以看出,随着旋转速度的增加,球体的飞行时间、发球距离都逐渐减小,但这两个量的变化规律是有所区别的。飞行时间随着旋转速度的增加,基本呈线性减少,旋转速度每增加3 r/s,飞行时间减少0.04 s左右;而发球距离的减少量则是不均匀的,呈负指数规律,即旋转速度每增加一定值,开始时发球距离减少得比较多,到后来减少量比刚开始少。图6是不同旋轉速度时发球球体的运动轨迹,也可以反映出和表2相同的规律。
4 结论
我们先通过数学建模,通过计算得到了三个模型:不考虑空气阻力、马格努斯力的基础模型;考虑空气阻力,不考虑马格努斯力的阻力模型;同时考虑空气阻力和马格努斯力的旋转模型的速度和位移的含时间参数t的参数方程解,并通过表格数值和图像的方式进行了简单的分析。我们现在可以得出如下结论:
4.1 阻力模型
其实也就是平时最常见的无攻击性的发球模型,由于空气阻力,飞行时间会略微加长,发球距离略微缩短但是没有明显变化,控制不得当比较容易出界。主要特点是发球难度小,但是攻击性差,给接球方冲击较小。
4.2 旋转模型
旋转速度越大,球体飞行时间越短,发球距离越小,且变化比较明显,可以达到20%以上。发球飞行时间随旋转速度基本呈线性减小,由于大力跳发时球体飞行时间本来就比较短,通过旋转进一步有效地缩短接球方的反应时间,使接球难度变大;发球距离随发球旋转速度的增减呈负指数关系变短,加上一点旋转就可以使得发球距离明显变短,这可以给我们一个很好的启示是,加上一点旋转可以使得发球更加不容易出界,这是发球加上旋转的第一个优点;其次,较强旋转时发球距离可以变化得非常明显,达到5 m以上,在较短时间内给防守队员的判断带去更大的困难,从而使得发球更加具有冲击性。
综上,旋转式发球相比与不旋转的发球,飞行时间减少,发球距离缩短,更加具有攻击性,运动员们在实际训练时可以结合本文与实际,多多感受旋转球的特点,从而使得训练更有针对性、更加有效。
参考文献:
[1]G. Magnus.On the deviation of projectiles, and on a remark-able phenomenon of rotating bodies[M].Memoirs of the RoyalAcademy,Berlin,1852:210.
[2]V. Timková, and Z. Jeková.How Magnus Bends the Flying BallExperimenting and Modeling[J].T-he Physics Teacher,2017(55):112.
[3]M. Nathan.The effect of spin on the flight of a baseball[J].Am.J.Phys,2008(76):119-124.
[4]P.Gluck.Air resistance on falling balls and balloons[J].Phys.Teach,2003(41):178-180.
[5]K. Takahashi,D.Thompson.Measuring air resistance ina computerized laboratory[J].Am. J. Phys,1999(67):709-711.
[6]Mario A,Aguirre-López .A cardioid-parametric model for the Magnus effect in baseballs[J].Advances in Computational Mathematicsere,2019:2097-2109.
[7]Christian Guzman. The Magnus effect and the American football[J].Sports Engineering,2016:13-20.
[8]Mustafa Turkyilmazoglu. Exact and approximate solutions to projectile motion in air incorporating Magnus effect[J].The European Physical Journal Plus,2020:155-170.
[9]何家梅,丁煥常.旋转球体的运动轨迹[J].许昌学院学报,2005(5):38-40.
[10]贾拴稳.有阻力的空气介质中质点的运动规律[J].安阳师范学院学报,2008(5):32-34.
[11]李文科.工程流体力学[M].合肥:中国科学技术大学出版社,2007:219-223.
[12]薛社教.用数学方法研究乒乓球上旋球的飞行轨迹[J].高教学刊,2016(6):263-264.
[13]韩阳.基于Magnus效应的摆动旋转圆柱实验教学平台[J].实验技术与管理,2020(9):54-57.
[14] 潘慧炬.马格努斯效应的力学模型[J].浙江体育科学,1995(3):16-19.
[15]吴洪波.网球发球运动轨迹动力学分析及仿真研究[J].计算机仿真,2017,34(3):243-246.
[16]郝成红,黄耀清,刘聚坤.考虑空气阻力的足球弧线球运动轨迹[J].大学物理,2018,37(6):19-21.
