对蛇形流道结构的DMFC中气泡段特性研究

陈海伦，孟庆然，王文东**，康 博，陈利强，田爱华*

(1.吉林化工学院 机电工程学院，吉林 吉林 132022；2.吉林梦溪工程管理有限公司，吉林 吉林 132001 )

随着DMFC(Direct Methanol Fuel Cell)在移动携带式电源领域的迅速发展，DMFC流道的截面尺寸缩小至毫米时，所带来的尺寸效应对反应物的传递产生了极大的影响[1-3].DMFC结构尺寸的缩小，会增大流道内的阻力，影响反应物向催化层的传质速度.在电流密度较高时，气泡生成的速度及脱离扩散层表面小孔的速度较快，使阳极流道中CO2气泡极易通过聚合形成气泡段，产生的气泡段将堵塞流道，从而阻碍了甲醇水溶液的传递[4-8].若反应物不能均匀地分布到流道中，会造成MEA局部的热量集中，极化现象严重，导致电池的性能降低，因此需要对流道结构进行合理的设计.

采用VOF方法对DMFC在蛇形流道中产生的气泡段进行3维等温数值模拟，研究分析了气泡段在蛇形流道中的运动情况及流道深度、台肩宽度对气泡段的运动特性及蛇形流道进口压力降的影响.

1 模型建立

1.1 几何模型

如图1所示为本文用到的蛇形流道的几何模型，所有模型的流道宽度均为0.4 mm、直流道部分的长度均为14 mm，在此基础上改变流道深度、台肩宽度进行对比研究.结合实验中气泡段的运动情况[8]，设定液相工质浓度为1 mol/L)，初始时刻的液相甲醇水溶液的进口速度为0.04 m/s，气相CO2的进口速度为0.1 m/s，所有壁面均采用无滑移速度，扩散层表面与上壁面的静态接触角度为50°、两侧壁面的静态接触角为75°.表1中的10种情况，按如下假设中进行模拟计算.

表1 工况表

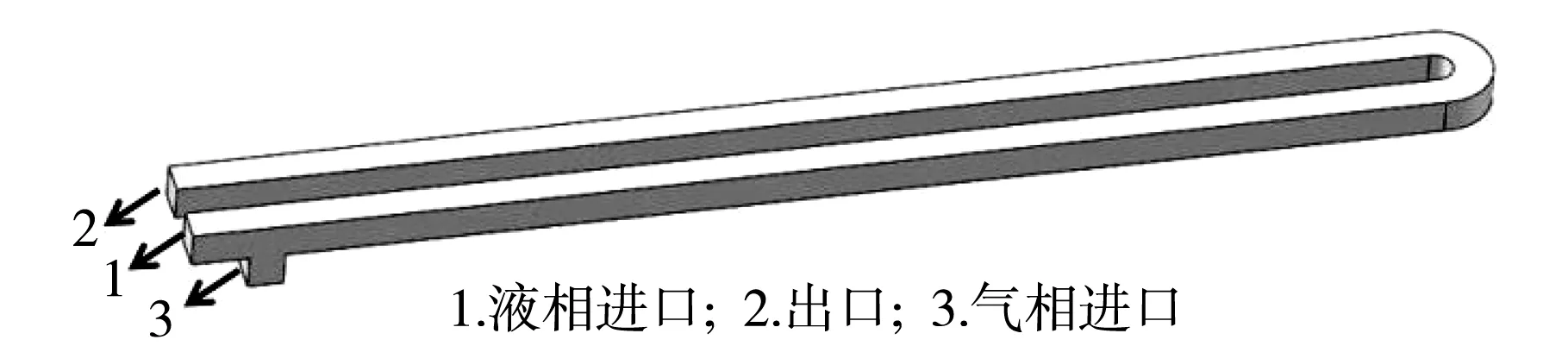
图1 气泡段模型

(1)由于蛇形流道入口处横截面积较小，气相进口速度、液相进口速度较低，计算蛇形流道内的雷诺数(Re)<2 000，因此流体流动方式为层流；

(2)由于气相进口速度、液相进口速度较小，因此气相、液相均可认为是不可压缩流体即气相、液相的密度恒定；

(3)由于流道尺寸较小，流道内流体的体积小，因此可忽略两相流的重力；

(4)经过模拟测试，本章节选取的时间步长为10-5s.

1.2 控制方程

对于直流道的流场，计算流道的进出口压降可采用计算管道内的压降方式；对于蛇形流道，流道可分为两个部分(直流道部分和转弯部分)，故蛇形流道内压降也可将这两部分分别计算，再相加得出.

每一部分的压力降均由3部分组成：摩擦压降、重力压降以及加速压降.由于研究的是水平蛇形流道且两相流的质量较轻，故假设重力压降为0.据文献所知[9]：加速压降不到摩擦压降的1%，因此可忽略加速压降.

对于蛇形流场中直流道部分的压力降，忽略了重力压降及加速压降，直流道部分压力降等于摩擦压力降，其公式如下[10]：

ΔPv=ΔPF,

(1)

(2)

其中G为质量流速、λ为每一相中摩擦阻力系数、φ为摩擦阻力压力降校正系数，对于四边形的通道φ=0.88、L为直流道的长度、τ为层流的曳力系数、dhyd为水力直径，其计算方式为

(3)

(4)

(5)

(6)

其中K为两相流界面的局部曲率、bm、hm为流道的宽度与深度、μ为运动粘度、φ为校正系数，与曳力系数和水力直径相配.

除了直流道产生的压力差，弯道处也产生压力差，压差可如下表示：

(7)

其中v为流体的平均速度、ξ为1～2，其大小取决于拐角的形状，本文研究转角为弧形，弧形为1，因此蛇形流道总压降：

ΔP总=ΔPv+ΔPcorner,

(8)

2 模拟分析结果

2.1 流道内气泡段的运动过程

气泡段脱离小孔，气泡段前、后接触面中的上下两个接触角的角度θ几乎一致，气泡段被气体填充，且由于流道壁面并不是完全亲水的，使得气泡段主体部分在壁面上没有明显的气膜.只要设定孔内逸出的单位气体体积流量不变，流道内气泡段就会随着液相推动产生一定的位移效应，气泡段与液柱会交替出现在流道内，一起向流道出口移动.

2.2 流道内气泡段的运动过程

如图2为截面积为0.4 mm × 0.4 mm，0.204 81 s时刻在y=0.2 mm的界面上的压力分布，由图可知，蛇形流道中压力分布是很有规律的，每一个气泡段中的压力分布均匀且气泡内压力分布随着移动成周期性下降，气泡段的压力比液柱的压力要大，在弯道处的液柱与其他位置的液柱压力差相比，压力差较大.把模拟中从气泡逸出小孔形成的气泡段开始端到下一个气泡段的开始端为一个单元即气泡段与相邻的液柱为有一个单元，从而来分析压力的变化.尽管沿通道的压力趋于减小，但气泡内部的压力高于液体内部的压力.

图2 截面积为0.4×0.4 mm，0.204 81 s时刻在y=0.2 mm的界面上的压力分布

如图3所示为截面积为0.4×0.4 mm，时刻为0.102 48 s，在y=0.2 mm的界面上的速度矢量图，一个速度矢量定向从低压场到高压场.这一现象反映了气液界面毛细管压力差与表面张力的关系.由于气相在上下表面接触角为75°，所以管中的气塞在头部和尾部都有凸面，这说明气体内部的压力与表面张力是平衡的.由图4a可以观察到在气泡段的表面处，气泡段与液柱之间相互作用力相互抵制，由图4b可知，气泡会以一定的速度冲向壁面，且速度较大，导致在转弯前后的两个单位的压降差大于其他相邻单位之间的压降差.

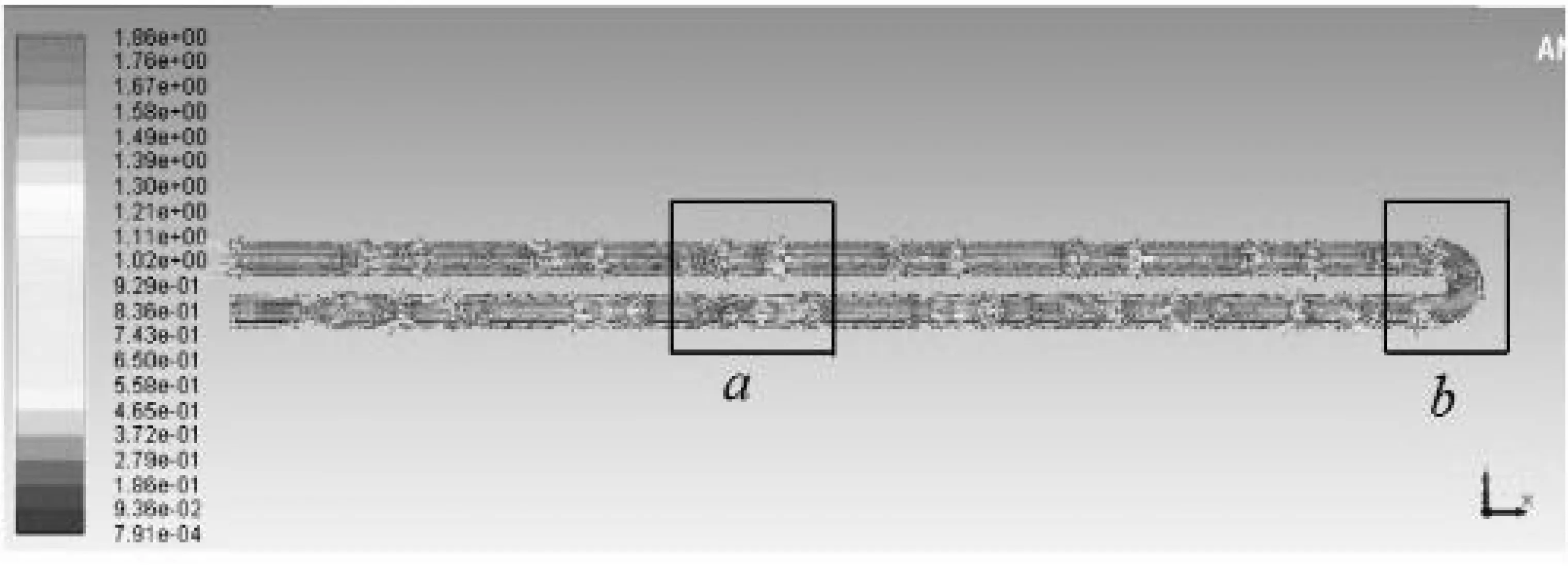
图3 截面积为0.4 mm×0.4 mm速度分布

(a)

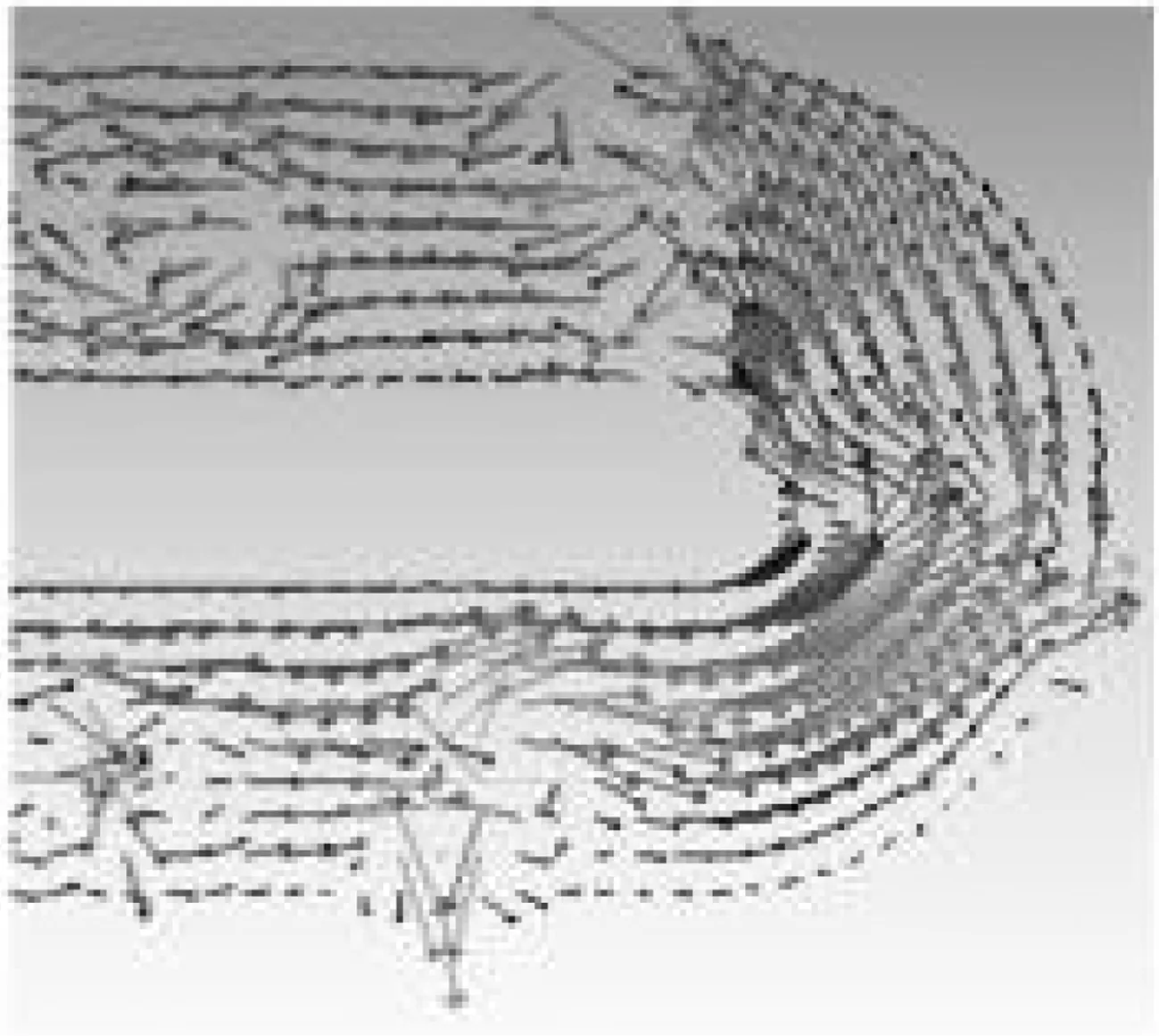
(b)图4 截面积为0.4 mm×0.4 mm速度分布的局部图

2.3 流道深度对蛇形流道内压降的影响

本节通过改变蛇形流道的深度研究蛇形流道进出口压力降的变化情况，情况1、情况2、情况3、情况4中流道深度分别为0.4 mm、0.2 mm、0.6 mm、0.8 mm.

如图5所示为第一个气泡段的位置随时间变化曲线图.由于流道深度的减小，气泡段与侧壁面的接触面积减小，表面张力减小，气泡段容易脱离小孔，导致气泡段流动速度增加.

时间/s图5 第一个气泡段的位置随时间变化曲线图

如图6所示为蛇形流道的不同深度对进出口压降影响的曲线图.由图5可知：随着深度的减小，进出口压降逐渐增大.不同流道深度影响了流道内的线速度及雷诺数(Re)，同时不同的流道深度也影响流道内的质量传输.换言之，通过减小流道深度即减小流道内的横截面积，使阳极流道内气泡段的线速度及雷诺数增加.由于速度较小，因此计算得出的雷诺数依旧在层流范围.本节模拟结果与Wang等[11]研究结果相似.在制作流道过程中，深度越浅，制作工艺越困难，对微型流道的制作工艺要求越高.

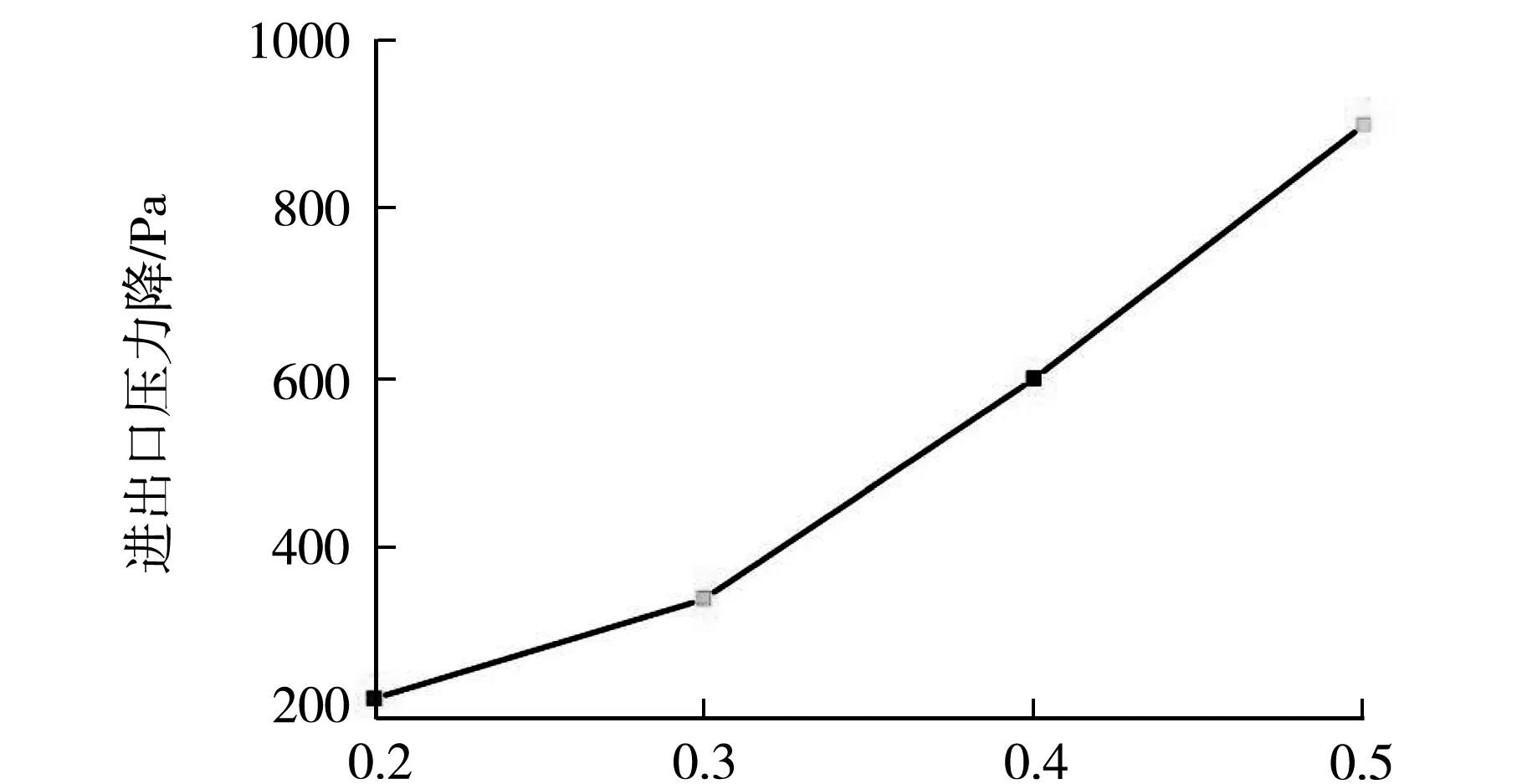
流道宽度/mm图6 深度对蛇形流道的进出口压降影响的曲线图

2.4 台肩宽度对蛇形流道内压降的影响

情况5、情况6、情况7、情况8、情况9、情况10中，流道深度相同，均为0.4 mm，台肩宽度分别为0.2 mm、0.25 mm、0.3 mm、0.35 mm、0.45 mm、0.5 mm，研究台肩宽度对气泡段流动的影响.

如图7所示为不同台肩宽度对第一个气泡段流出流道的时间及对蛇形流道进出口压降的影响曲线图，台肩宽度为0.35 mm时，第一个气泡段排出流道的时间最短，进出口压降较大，换言之，台肩宽度与流道宽度接近时，其排出速度较快，且进出口压力降较大.在设计蛇形流道时，建议设计台肩宽度是流道宽度的0.75～1倍.

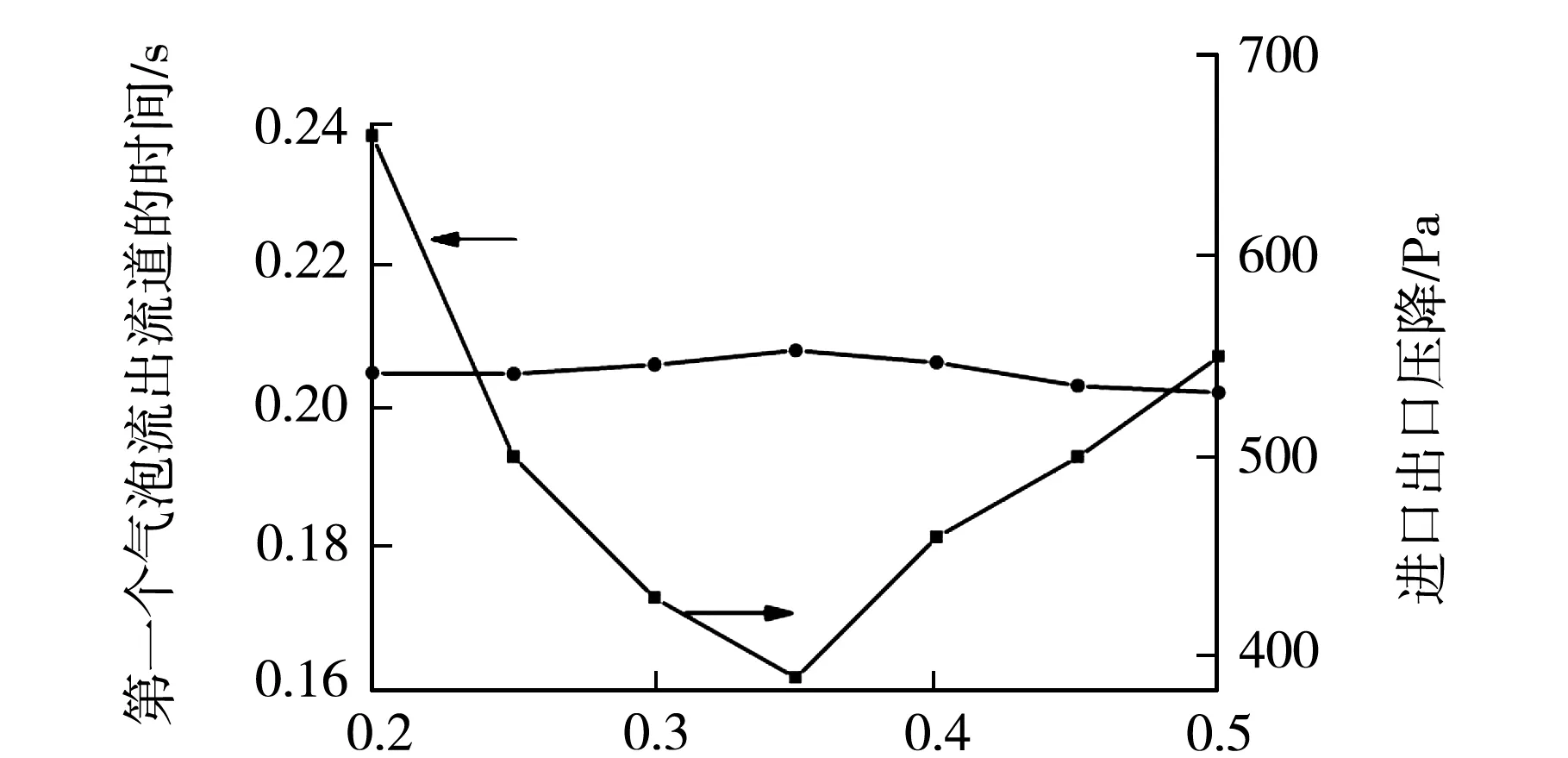
台肩宽度/mm图7 不同台肩宽度对第一个气泡段流出流道的时间及对蛇形流道进出口压降的影响曲线图

3 结 论

在微型DMFC阳极流道中，小气泡会不断发生聚合，最后形成气泡段，它也是流道中气体的常态.影响气泡段运动特性的因素一方面是操作条件，另一方面是流道结构尺寸，主要研究流道结构对气泡段的影响，研究结果如下：

(1)随着流道深度的减小，蛇形流道的进出口压力降增大，因此在设计工艺允许的条件下，可以尽量减小流道深度.

(2)台肩宽度与流道宽度相近时即台肩宽度为流道宽度的0.75～1倍时，气泡段排出流道时间较短，且进出口压力降较大.