大内倾角钢箱提篮拱几何非线性稳定分析

吴海军， 唐海淘， 何立

(重庆交通大学 土木工程学院， 重庆 400074)

近年来，城市桥梁设计越来越注重文化传承和美学设计，钢箱梁提篮拱桥以其优美的造型、良好的经济指标而成为一种热门桥型方案，研究提篮拱的空间稳定性愈发重要。彭容新等对箱形拱肋提篮拱桥的非线性稳定性进行研究，得出拱肋结构的稳定性由横向稳定决定，成桥阶段荷载作用下的稳定性则由拱肋结构的竖向稳定决定；同时发现内倾角为15°时，考虑几何非线性时横向稳定性的临界失稳荷载是其特征值的数倍。曹正洲等对影响结构整体稳定性的因素进行研究，得出拱肋内倾角变化对稳定性的影响较大，内倾角增大，结构1阶稳定系数增加，但过大的内倾角将导致拱肋扭转失稳；随着矢跨比(宽跨比)的增加，结构1阶稳定系数增大(减小)；横撑、吊杆布置形式对结构稳定性的影响较小。张庆明等研究内倾角对提篮拱稳定性的影响，得出不考虑非线性影响时，内倾角以10°左右为宜。目前对于内倾角大于15°的大倾角提篮拱桥的研究较少。该文以大倾角中承式钢箱梁提篮拱桥为研究对象，考虑几何非线性的影响，分析不同荷载、矢跨比、拱肋内倾角对提篮拱肋稳定特性的影响。

1 稳定性分析方法

1.1 特征值屈曲分析

结构稳定性分析分为第一类稳定(分支点稳定)和第二类稳定(极值点稳定)，在实际工程中，由于拱结构构件初始缺陷、荷载作用位置偏离等原因，第一类稳定问题一般不存在。但其临界荷载值可近似反映第二类稳定的上限，因而具有较大的参考价值。第一类稳定问题在力学上较明确，在数学上是齐次方程的特征值问题，求解方便，可利用结构线弹性屈曲分析解决第一类稳定问题。

根据线性屈曲理论，拱桥结构在外荷载作用下的特征方程为：

([Kt]+λ[Kg]){δ}=0

(1)

式中：[Kt]为弹性刚度矩阵；λ为特征值(稳定系数)；[Kg]为几何刚度矩阵；{δ}为位移增量列阵。

要使式(1)有非零解，应有：

|[Kt]+λ[Kg]|=0

(2)

此时，δ将趋于无穷大，结构失去稳定性。假定式(2)有n阶，则必有n个特征解。对于实际工程，只有最小解才有意义，因而可只考虑1阶特征值的大小。

1.2 几何非线性屈曲分析

几何非线性即结构因几何变形而引起的刚度变化，分为大位移小应变问题、大位移大应变问题，不再满足小变形假定。考虑几何非线性后，拱桥结构的非线性方程见式(3)，求解方法主要有增量法、迭代法和混合法。

([Kt]+[KL]+[Kg]){δ}={F}

式中：[KL]为位移矩阵；{δ}为节点位移列阵；{F}为等效节点荷载列阵。

2 有限元计算模型

2.1 桥梁概况

某提篮拱拱肋采用变截面钢箱截面，拱轴线采用二次抛物线，计算跨径为132.97 m，矢高为52.1 m，矢跨比为1/2.552。主孔横桥向设置2片钢拱肋，内、外侧腹板分别向内倾21.7°和23.8°。为满足景观要求，主跨桥面2个拱肋间不设风撑，仅在拱顶位置将两拱肋连接。2个主拱拱肋与钢箱梁之间除吊杆连接外，其余部分均独立开来(见图1)。

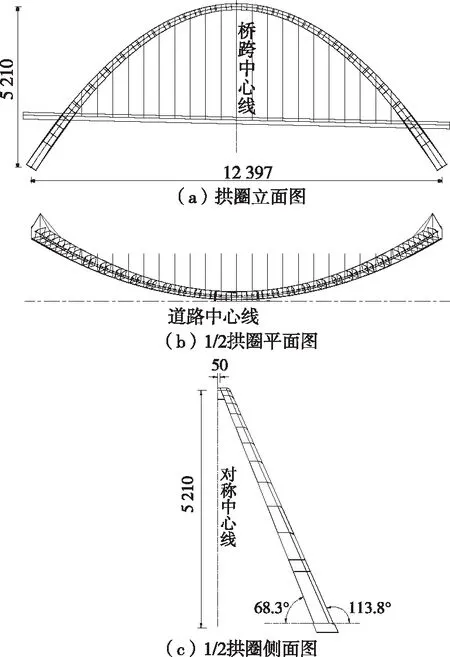
图1 钢箱梁提篮拱桥提篮拱肋布置(单位：cm)

2.2 空间有限元模型的建立

应用MIDAS/Civil程序建立该桥有限元计算模型，根据其结构特点和施工工艺要求，建模中考虑拱箱内加劲肋的影响。主拱肋、肋间横撑采用空间梁单元模拟，两岸拱脚固结。结构离散后，全桥共有梁单元221个、节点218个(见图2)。

图2 钢箱梁提篮拱桥有限元模型

3 计算结果分析

3.1 线性屈曲分析

对该桥拱肋结构进行屈曲分析，在其中一条拱肋的拱顶处分别作用力值相等的竖向荷载、横向荷载及横向、竖向的双向荷载。以自重为不变量、拱顶荷载为可变量，其稳定系数计算结果见表1。

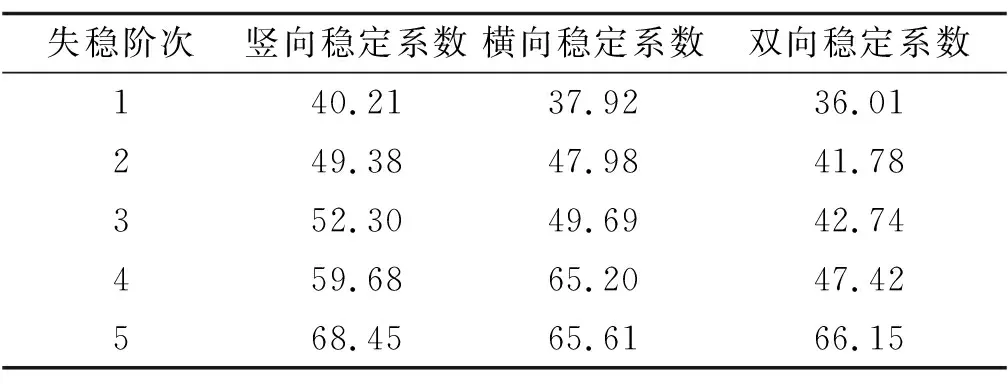
表1 钢箱梁提篮拱桥前5阶稳定系数

由表1可知：各荷载作用下，1阶稳定系数较接近；在横向、竖向双向荷载作用下，1阶稳定系数与横向、竖向时相比均有所下降，接近横向稳定系数。前5阶竖向稳定系数均大于横向稳定系数，前4阶双向稳定系数明显小于横向和竖向稳定系数，5阶双向稳定系数接近横向和竖向稳定系数，且大于横向稳定系数。

3.2 几何非线性屈曲分析

将拱肋结构弹性失稳系数的10%变形作为结构初始缺陷计入非线性分析，运用Newton-Raphson迭代法进行计算。步骤如下：定义非线性荷载加载顺序；设定荷载控制工况，并设置加载步骤数量和子步骤内迭代次数，定义收敛准则，制定程序终止选项；求解并查看结果。该方法需通过查看最不利节点位移是否发散来判断结构是否屈曲。在定义荷载变量时，需手动通过改变荷载值达到加载的过程，通过试算不断逼近其临界荷载。

考虑几何非线性，拱肋结构在不同荷载作用下的临界荷载见表2。由表2可知：双向荷载作用下极限荷载均小于竖向、横向荷载作用下临界荷载，与线性屈曲分析1阶稳定系数的规律相同。在拱顶竖向荷载、横向荷载及双向荷载作用下的极限荷载相较于线性屈曲分析结果下降幅度较大，均在30%以上，作用双向荷载时下降幅度达到43.45%，与线性结果相差较大。大内倾角提篮拱稳定性分析中不能忽略几何非线性的影响。

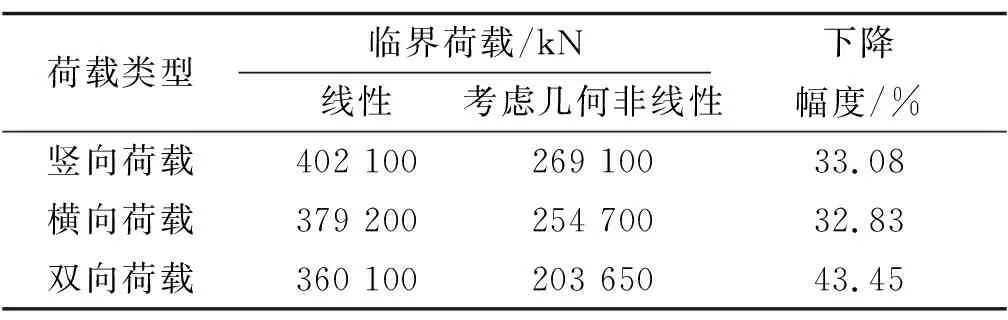
表2 线性屈曲与几何非线性屈曲极限荷载对比

根据一阶失稳时拱肋形态，仅作用竖向荷载时为面内失稳，作用横向、双向荷载时为面外失稳。考虑几何非线性后，拱顶在不同荷载作用下的荷载-位移曲线见图3、图4。由图3、图4可知：作用双向荷载时的竖向位移前期接近于作用竖向荷载时的拱顶位移，但总体位移更接近于作用横向荷载时的拱顶位移。

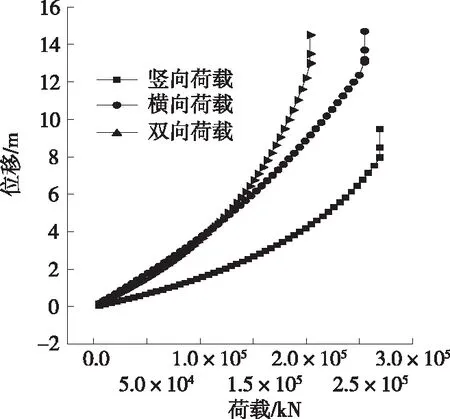
图3 荷载-位移曲线

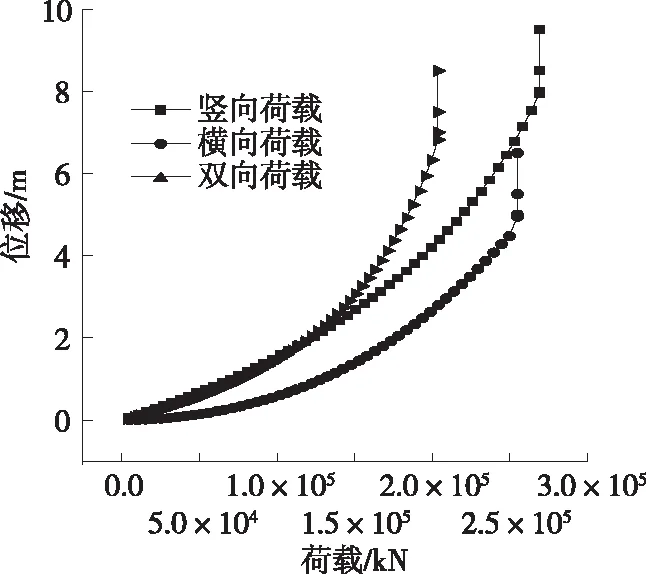
图4 荷载-竖向位移曲线

3.3 矢跨比对提篮拱稳定的影响

为更好地反映矢跨比对大内倾角提篮拱稳定的影响，在原结构的基础上，调整拱轴线方程，使其矢跨比分别为1/2.5、1/3、1/3.5、1/4、1/4.5、1/5，计算其特征值和考虑几何非线性后拱肋的失稳临界荷载，结果见图5。由图5可知：作用竖向荷载和双向荷载时的稳定性能随着矢跨比的减小而下降，且下降幅度较大；作用横向荷载时，其稳定性能随着矢跨比的减小而增大，但增加幅度较小。

对比线性稳定与考虑几何非线性后的临界失稳荷载，考虑几何非线性后的下降幅度见图6。由图6可知：作用竖向荷载和双向荷载时，考虑几何非线性后其稳定性能的下降幅度随着矢跨比的减小而增加，且作用双向荷载时更明显，减小幅度超过50%；作用横向荷载时，几何非线性的影响相对较小，但也超过30%。对于大内倾角提篮拱，其稳定性能必须考虑几何非线性的影响。从稳定性角度，大内倾角提篮拱桥合理的矢跨比为1/3左右，矢跨比小于1/3时，其横向稳定性能变化不显著，但竖向稳定性能急剧下降。

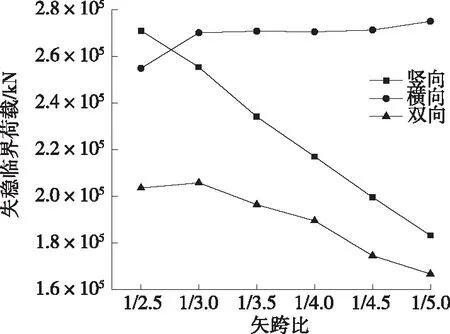
图5 不同矢跨比对应的临界荷载

图6 考虑几何非线性后稳定性能下降幅度

3.4 内倾角对提篮拱稳定的影响

为进一步探索拱肋倾角对提篮拱稳定的影响，保持拱脚位置不变，调整拱肋的内倾角，计算其在竖向和横向荷载作用下的失稳临界荷载，结果见图7、图8。

由图7可知：考虑几何非线性后，竖向临界失稳荷载均不同程度降低，但总体变化规律与线性屈曲分析规律一致。随着内倾角的增大，其竖向稳定性能逐渐增大，内倾角大于20°时竖向稳定性增强幅度减小。

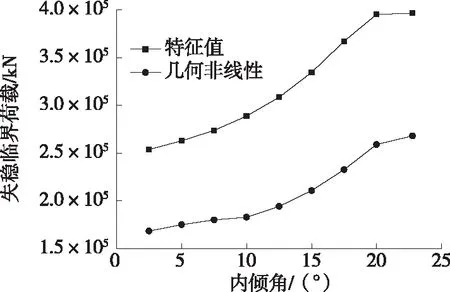
图7 不同内倾角对应的竖向临界荷载

图8 不同内倾角对应的横向临界荷载

由图8可知：考虑几何非线性后，横向临界失稳荷载差异较大。内倾角小于20°时，考虑几何非线性后临界荷载大于特征值，10°～15°时临界失稳荷载明显提高，12.5°左右时最显著，其失稳临界荷载提高2倍以上；内倾角大于20°时，考虑几何非线性后临界荷载小于其特征值。

考虑几何非线性，内倾角分别为5°、10°、15°、20°时的荷载-位移曲线见图9、图10。由图9、图10可知：考虑几何非线性后，在竖向荷载作用下，随着内倾角的增大，其失稳临界荷载逐渐增大，15°～20°时增长幅度最大；在横向荷载作用下，内倾角为10°～15°时，失稳临界荷载比其他角度时最高大3倍。其原因是未作用荷载的拱肋在作用荷载拱肋失稳时迅速参与工作，失稳临界荷载提高。

图9 竖向荷载作用下荷载-位移曲线

图10 横向荷载作用下荷载-位移曲线

4 结论

(1) 内倾角为21.7°的大内倾角提篮拱结构的横向稳定性低于竖向稳定性，横向、竖向双向荷载作用下的稳定性系数最低，与横向稳定系数接近，同时其荷载-位移曲线与横向稳定更接近。考虑几何非线性后，其失稳临界荷载下降明显，均在30%以上。

(2) 对于大内倾角提篮拱结构，随着矢跨比的减小，作用竖向荷载和双向荷载的稳定性能均明显下降，竖向稳定性能下降幅度更显著；作用横向荷载时的稳定性能有小幅度提高。考虑几何非线性后的下降幅度随着矢跨比的减小而增加，但矢跨比小于1/4.5时，作用双向荷载时的减小幅度超过50%。对于大内倾角提篮拱，从稳定性的角度，合理的矢跨比为1/3左右。

(3) 提篮拱作用竖向荷载时，随着内倾角的增大，提篮拱的竖向1阶稳定系数增大。考虑几何非线性后，其总体规律与线性屈曲分析相同，呈逐渐上升的趋势，15°～20°时增长幅度最快，大于20°时稳定性能开始下降。对不同内倾角，考虑几何非线性后，其竖向失稳临界荷载下降非常明显，均在30%以上。计算提篮拱竖向稳定特性时不能忽略几何非线性的影响。

(4) 提篮拱作用横向荷载时，考虑几何非线性后，内倾角为10°～15°时，由于提篮拱2条拱肋协调受力，其失稳临界荷载大于线性屈曲分析结果。对于该角度范围的提篮拱桥，横向稳定不考虑几何非线性是偏于安全的。但内倾角大于20°时，考虑几何非线性的结果小于其特征值，横向稳定分析需考虑几何非线性的影响。