框架梁悬空对预应力锚索框架内力影响的数值研究*
2021-02-23王华李智远
王华, 李智远
(1.贵州省质安交通工程监控检测中心有限责任公司, 贵州 贵阳 550000;2. 中南大学 土木工程学院, 湖南 长沙 410004)
预应力锚索框架梁是岩土锚固工程中非常重要的分支,以其安全可靠、加固合理等优点被广泛应用于边坡治理。在预应力锚索框架服役过程中,受运营环境和管理水平影响,其预应力会发生损失,且支护结构会发生老化,使锚固效果降低,严重时会导致预应力锚索框架失效而引起边坡失稳。预应力锚索框架内力计算及预应力锚索框架加固边坡稳定性分析是当前主要研究方向,如朱晗迓等讨论了锚墩框架梁系统的受力机理,结合监测数据,研究了锚墩在锚索预应力扩散中的分担作用,并利用Winkler弹性地基梁理论计算了梁体内力;黄志毅、马洪生结合离心模型试验,验证了初参数法弹性地基梁内力求解方法对预应力锚索框架梁的适用性,并分析了框架梁和地基的力学参数对梁体内力的影响;丁秀美等使用FLAC3D快速拉格朗日差分程序对预应力锚索框架作用下坡体附加应力分布进行了初步研究;吕庆等通过现场试验,研究了不同预应力锚固结构作用下不同弹性模量的裂隙岩质边坡压缩变形规律及附加应力,讨论了预应力锚索间距和框架梁高度对边坡表面压缩效应的影响。调研结果表明山区开挖路堑时难以保证边坡坡面的完全平整,致使预应力锚索框架梁与坡面之间常存在接触不密实的情况,不仅会导致框架梁受力状况改变,还会影响框架梁本身的健康状况。而目前对这一问题鲜有研究。为此,该文采用FLAC3D建立多工况数值模型,研究框架梁悬空对预应力锚索框架内力的影响。
1 研究背景
边坡防护工程中,由于施工工艺欠佳或坡体表面不平整,预应力锚索框架与坡体往往不能完全接触。同时由于岩土体是散体,在预应力锚索框架营运阶段长时间经历雨水冲刷后,梁体底部的松散土体可能会被掏空,造成框架梁体悬空,减小了梁体与坡体的受力面,改变了梁体的支撑条件,使梁体内力增大导致梁体破坏,也可能导致梁体整体下滑。图1为贵州省某地区框架梁底破坏后梁体下滑情况。

图1 框架梁底破坏后梁体下滑
通过实地调查,根据悬空位置不同将其分为悬臂端悬空、锚头下方悬空和跨中悬空(见图2)。
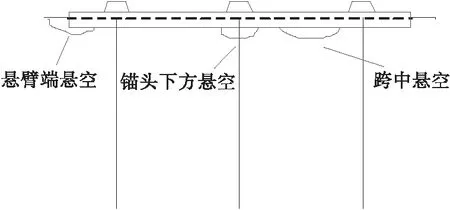
图2 框架梁悬空示意图
2 梁体悬空数值模拟
2.1 模型建立
以贵州省常见公路边坡形式为分析对象,采用FLAC3D建立数值模型(见图3),模型尺寸与边界条件见图4。垂直于纸面向里为Y轴正方向,Y方向宽度为8.5 m,框架梁居中布置于坡表面,边坡坡率为1∶1.0,坡高10 m,边坡坡后角为零。固定底部X、Y、Z方向,左右侧X方向及前后侧Y方向位移。
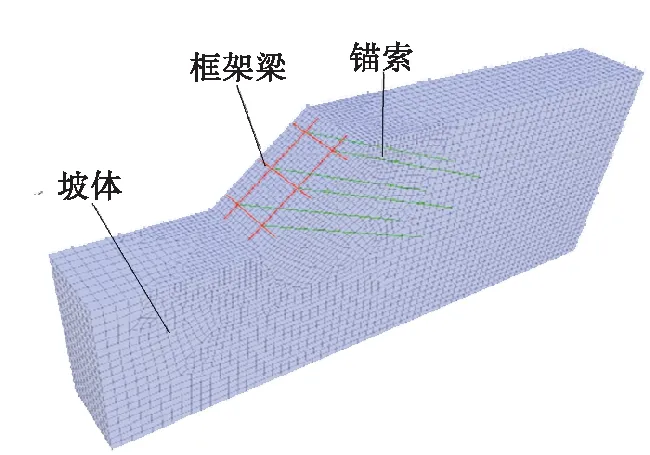
图3 公路边坡数值模型
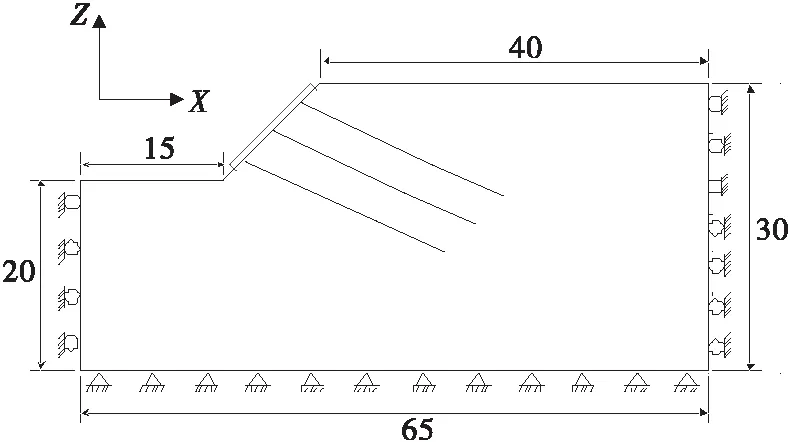
图4 数值模型尺寸与边界条件(单位:m)
为计算简化,建模时作如下假定:1) 鉴于主要研究对象为均质边坡,岩土体采用Mohr-Coulomb本构模型;2) 不考虑锚索框架自身重力及与坡面的摩擦力;3) 岩土体在自重作用下已固结完成。
2.2 参数赋值
参考《工程岩体分级标准》中Ⅳ、Ⅴ级岩体的力学参数范围,设定岩土体密度为2 250 kg/m3,强度参数见表1。

表1 岩土体的强度参数
模拟锚索时,锚索单元的内锚固段长取8m,自由段长取15 m,锚固角(锚索与水平面的交角)取25°,锚固段砂浆外圈直径取13 cm。6股锚索规格相同,根据GB/T 5224-2014《预应力混凝土用钢绞线》,选用规格为:高强度低松弛标准型钢铰线,记为UPS15.20-1860,为由7根钢丝捻制的标准型钢绞线,强度级别为1 860 MPa,公称直径Dm=15.20 mm,截面参考面积Sm=140 mm2。根据规范设定的锚索单元参数见表2。
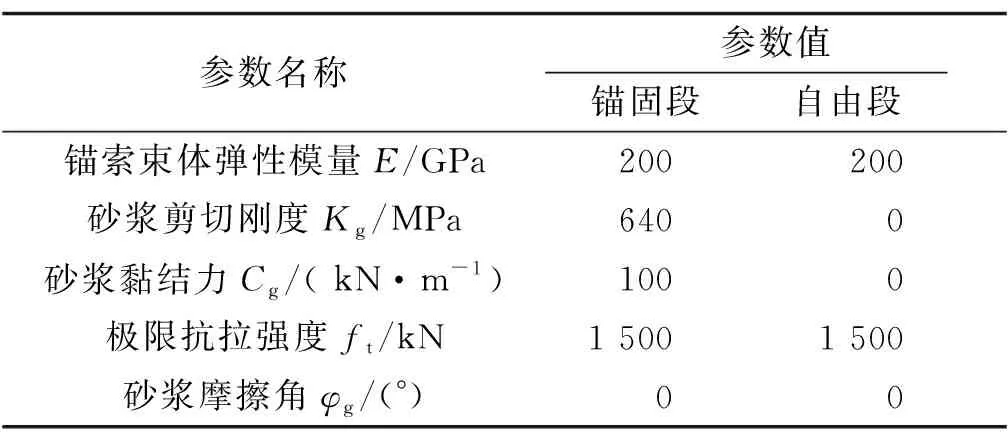
表2 锚索单元参数
采用内置的梁单元模拟框架梁,模型中框架梁沿坡面放置,框架梁尺寸及布置见图5。梁截面尺寸为50 cm×50 cm,采用对称配筋。
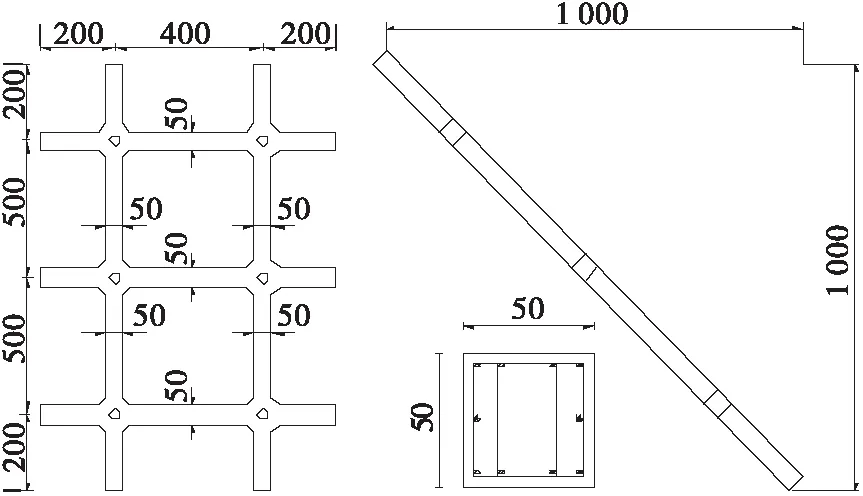
图5 框架梁尺寸(单位:cm)
梁单元的参数参考C30砼,考虑配筋对砼弹性模量的提升可达10%左右,钢筋砼弹性模量取32.4 GPa。框架梁梁单元参数见表3。
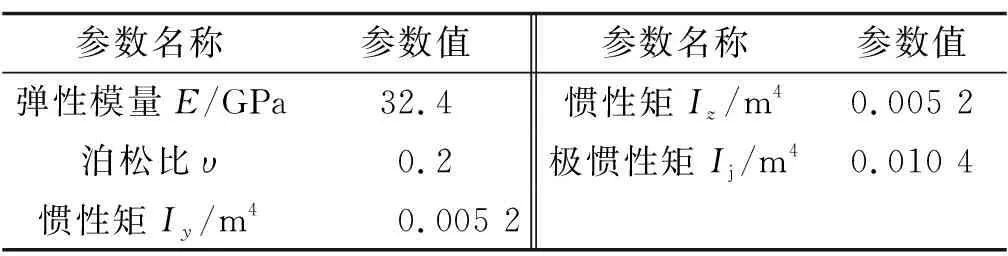
表3 框架梁梁单元参数
FLAC3D中,结构单元之间、结构单元与岩土体单元之间的相互作用通过设置节点连接来实现。在预应力锚索框架梁支护结构模拟中,将梁节点与坡面刚接实现二者同步变位,将锚索索头节点与相应梁单元节点刚性连接实现锚头和梁体的协调变形。图6为预应力锚索框架加固边坡的坡面正视图,其中黑色圆点为梁单元的节点。坡面宽8.5 m,进行17等分,坡面高14.14 m,进行29等分,则每个岩土体网格近似为0.5 m×0.5 m正方形。框架梁纵梁长14 m,等分为28个子单元,横梁长8 m,等分为16个子单元,每个节点均位于岩土体网格中心。锚索锁定后的预应力值取500 kN。
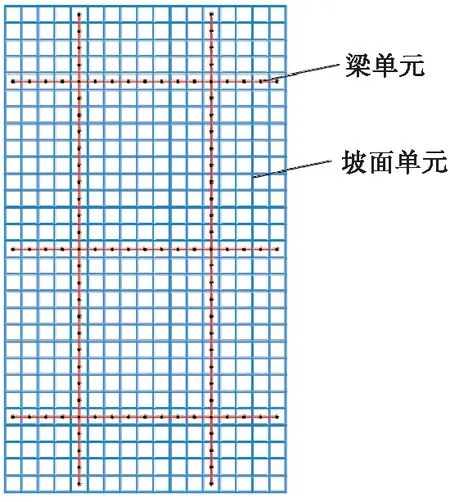
图6 框架梁与坡体耦合关系示意图
2.3 求解过程及监测点布置
通过删除与梁单元节点连接的岩土体单元模拟对应的梁单元节点脱离岩土体,针对纵梁悬臂端、横梁悬臂端、锚头下方、纵梁跨中和横梁跨中悬空工况研究框架梁悬空对预应力锚索框架内力的影响。
各梁体悬空工况下框架梁内力的求解过程如下:1) 建立预应力锚索框架加固边坡模型,预设锚索单元的轴向力,此时整个力学模型并未达到平衡状态,进行求解,得到初始无悬空状态下预应力锚索框架的内力。2) 保持其他参数不变,删除各工况对应的岩土体单元,重新进行求解,得到悬空工况下预应力锚索框架的内力。
因为框架梁悬空的位置不同,对纵梁和横梁内力的影响规律不一样,对纵梁和横梁弯矩分别进行监测,定义右侧纵梁为1#梁,下部横梁为2#梁,中部横梁为3#梁(见图7)。
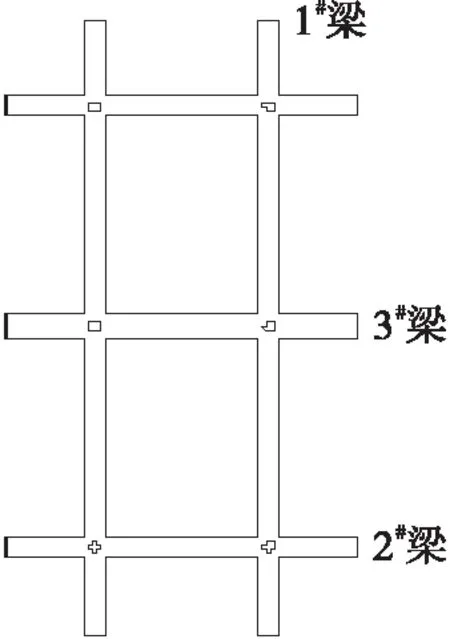
图7 梁体的编号
2.4 工况建立
(1) 锚头下方悬空工况。6个锚头处悬空状况相同,以锚头为圆心,半径0.5、1.0、1.5、2.0 m内梁体悬空,对应模拟工况见图8。由于篇幅有限,仅给出部分悬空半径示意图。沿半径方向每删除一个岩土体单元,悬空半径增加0.5 m。
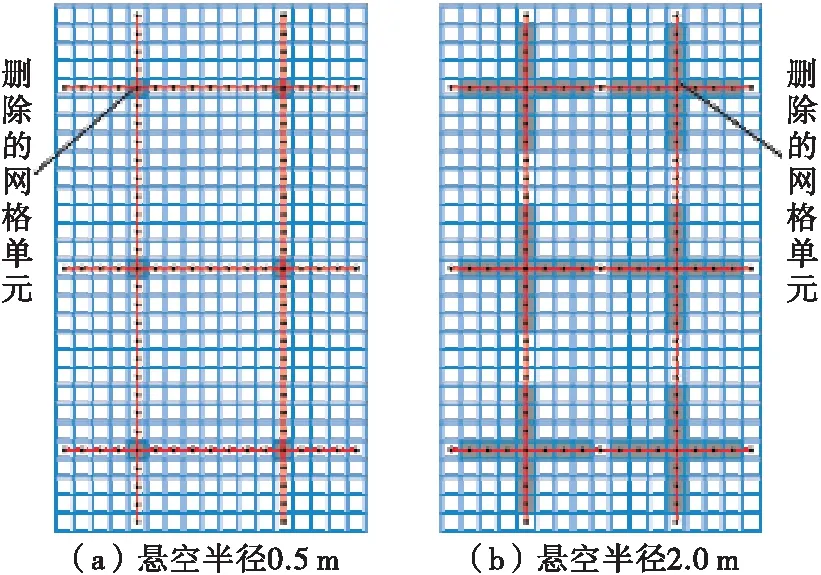
图8 锚头下方悬空工况数值模型
(2) 纵梁悬臂端悬空工况。4个纵梁悬臂端悬空状况相同,以纵梁悬臂端端点为圆心,半径0.5、1.0、1.5、2.0 m内梁体悬空,部分模型见图9。
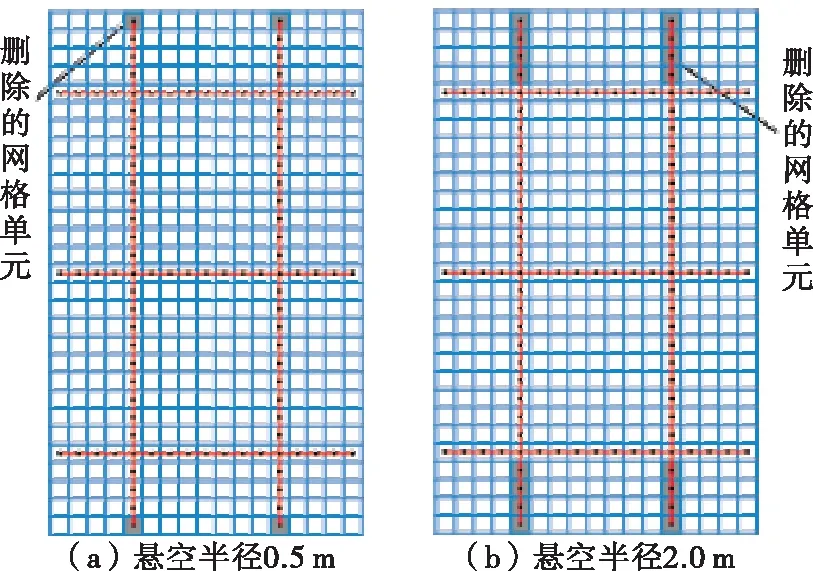
图9 纵梁悬臂端悬空工况数值模型
(3) 横梁悬臂端悬空工况。6个横梁悬臂端悬空状况相同,以横梁悬臂端端点为圆心,半径0.5、1.0、1.5、2.0 m内梁体悬空,部分模型见图10。
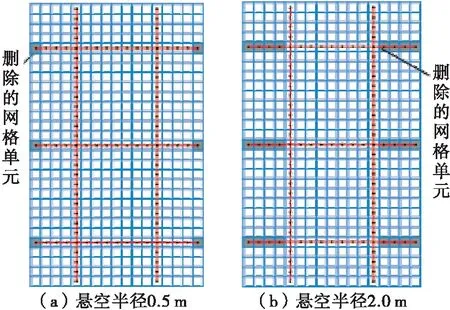
图10 横梁悬臂端悬空工况数值模型
(4) 纵梁跨中悬空工况。4个纵梁跨中悬空状况相同,以纵梁跨中为圆心,半径0.5、1.0、1.5、2.0、2.5 m内梁体悬空,部分模型见图11。
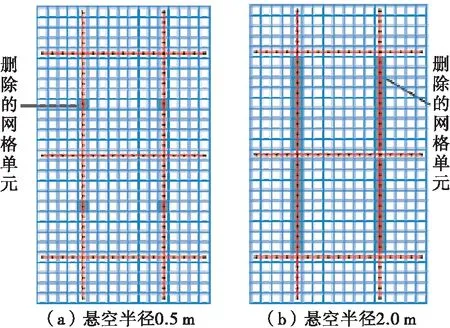
图11 纵梁跨中悬空工况数值模型
(5) 横梁跨中悬空工况。3个横梁跨中悬空状况相同,以横梁跨中为圆心,半径0.5、1.0、1.5、2.0 m内梁体悬空,部分模型见图12。
图12 横梁跨中悬空工况数值模型
3 各位置梁体悬空对梁体弯矩的影响
3.1 锚头下方悬空对梁体弯矩的影响
不同锚头下方悬空半径下梁体内力见图13,定义框架梁靠近坡侧受拉弯矩为正。由图13可知:锚头下方悬空,纵梁锚头下方截面、跨中截面、横梁锚头下方截面、跨中截面弯矩绝对值均增大。
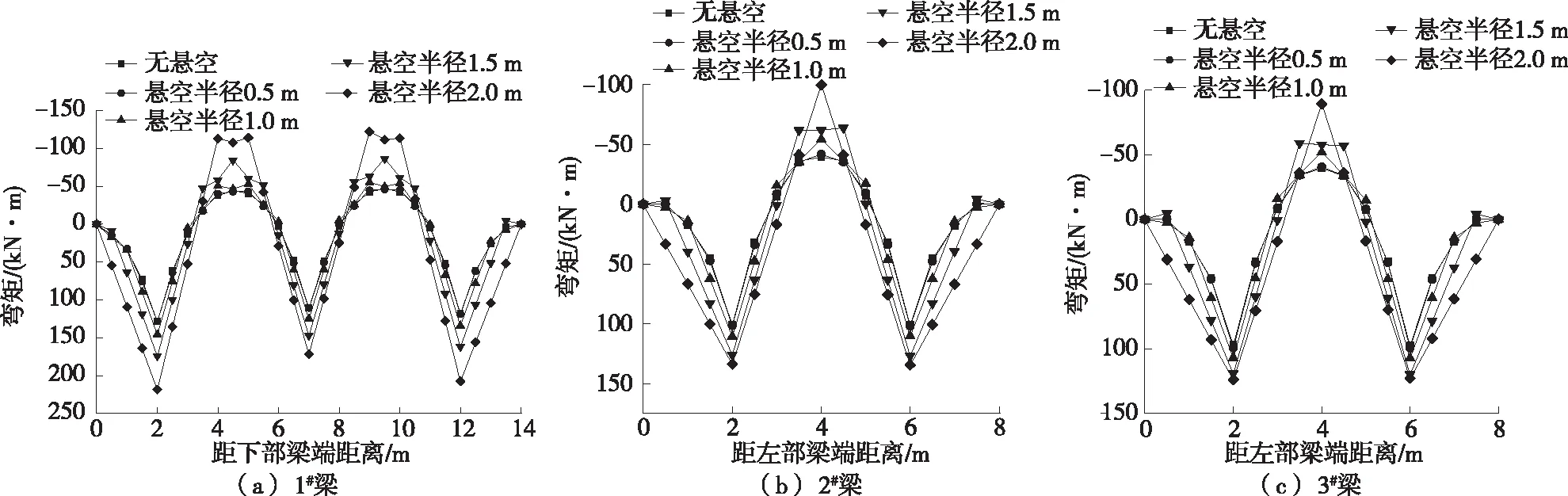
图13 不同锚头下方悬空半径下各梁弯矩
3.2 悬臂端悬空对梁体弯矩的影响
不同纵梁悬臂端悬空半径下梁体内力见图14。由图14可知:纵梁悬臂端悬空,纵梁两端负弯矩变大,正弯矩变小,中部弯矩变化不明显;下部横梁锚头下方和跨中弯矩绝对值增大;中部横梁弯矩变化不明显。
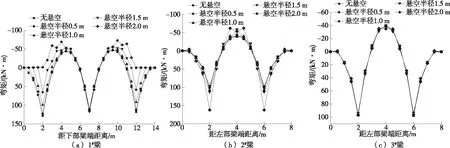
图14 不同纵梁悬臂端悬空半径下各梁弯矩
不同横梁悬臂端悬空半径下梁体内力见图15。
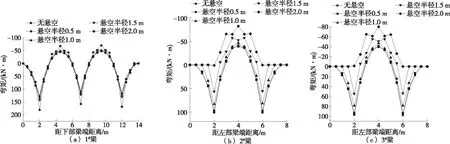
图15 不同横梁悬臂端悬空半径下各梁弯矩
由图15可知:横梁悬臂端悬空,纵梁正、负弯矩均变大;横梁锚头下方弯矩绝对值变小,跨中弯矩绝对值变大。悬臂端悬空在忽略梁体自重的情况下可等效为悬臂梁长度变短,变化规律与使用Winkler弹性地基梁模型的研究结论一致,说明通过删除与梁单元节点连接的岩土体单元模拟对应的梁体脱离土体悬空的方法可行。
3.3 跨中悬空对梁体弯矩的影响
不同纵梁跨中悬空半径下梁体弯矩见图16。由图16可知:纵梁跨中悬空,纵梁正、负弯矩绝对值均减小,且中间锚头下方与跨中弯矩有变号趋势;横梁正、负弯矩绝对值均增大。
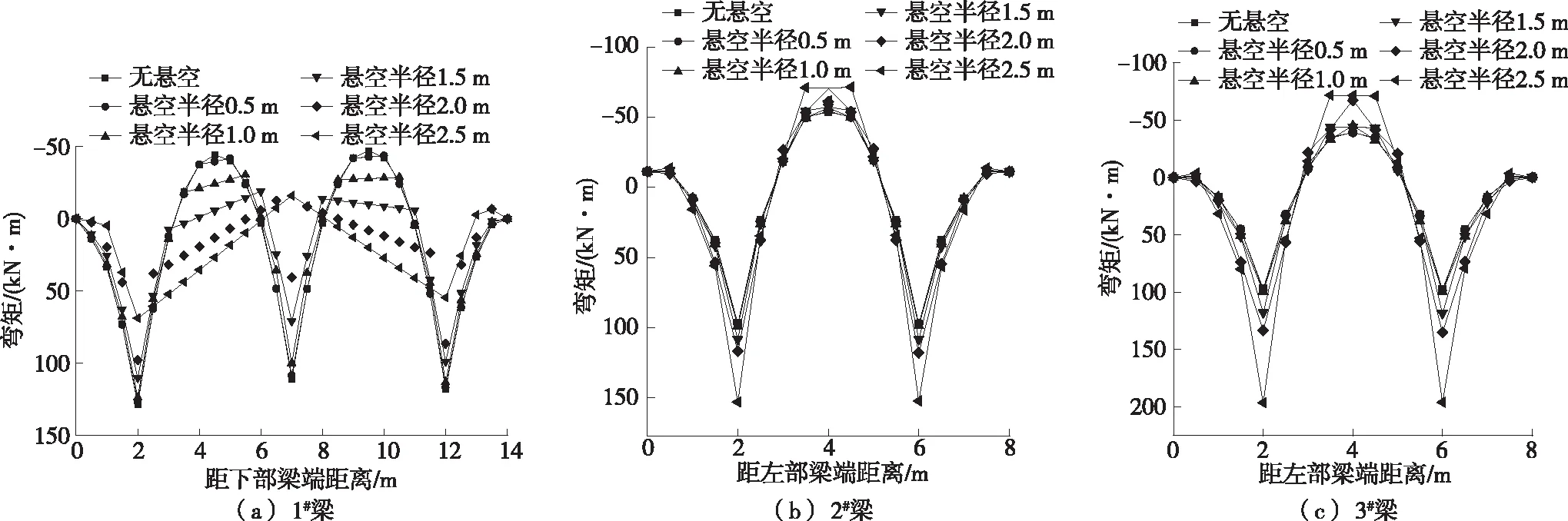
图16 不同纵梁跨中悬空半径下各梁弯矩
横梁跨中悬空,弯矩变化与纵梁跨中悬空相似,横梁正、负弯矩绝对值均减小,且跨中弯矩有变号趋势;纵梁正、负弯矩绝对值均增大。因篇幅限制,图表不再列出。
4 悬空位置对梁体弯矩影响程度比较
定义使任意梁形成简支约束或使整个悬臂段悬空的工况悬空半径为这类工况的最大悬空半径,则锚头下方悬空、横梁跨中悬空、横梁悬臂端悬空和纵梁悬臂端悬空所能达到的最大悬空半径为2 m,纵梁跨中悬空所能达到的最大悬空半径为2.5 m。定义i工况的实际悬空半径ri与这类工况所能达到的最大悬空半径rmax的比例为悬空比rr,即
rr=ri/rmax×100%
(1)
定义各悬空工况下框架梁最大弯矩绝对值Mi与无悬空工况下框架梁最大弯矩Mmax的比值为最大弯矩相对比例Mr,即
Mr=Mi/Mmax×100%
(2)
各工况下最大弯矩相对比例见图17。由图17可知:锚头下方悬空造成的框架最大弯矩绝对值增长程度比悬臂端和跨中悬空时大,对梁体内力的影响大,为最不利悬空位置。
5 结论
基于FLAC3D建立数值模型,通过删除与梁单元节点连接的岩土体单元模拟框架梁悬空,研究各部位悬空对框架梁内力的影响。结论如下:
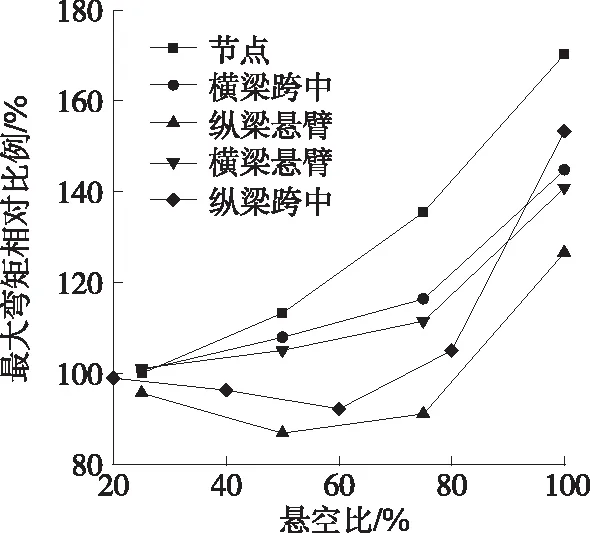
图17 各工况下最大弯矩相对比例
(1) 锚头下方悬空导致所有梁体的弯矩绝对值都增大,悬臂端和跨中悬空导致部分梁体弯矩绝对值增大、部分减小。
(2) 相对于悬臂和跨中悬空,锚头下方悬空造成的框架最大弯矩绝对值增长程度较大,锚头下方悬空对梁体内力的影响大于悬臂悬空和跨中悬空,对梁体内力的影响大,为最不利悬空位置。
