基于散射电场的飞机旋翼多普勒回波模拟

2021-02-23谢黄海代朝阳

科学技术与工程 2021年2期

刘钢, 唐波,2*, 谢黄海, 代朝阳

(1.三峡大学电气与新能源学院，宜昌 443002；2.三峡大学湖北省输电线路工程技术研究中心, 宜昌 443002)

在防空雷达系统中，为确定未知旋翼飞机目标的敌我属性关系，需利用飞机旋翼高速旋转而产生的多普勒回波信号，从中提取出目标的属性特征，进而实现目标的识别[1-2]。因此，准确获取旋翼飞机的回波，是旋翼类飞机目标识别的关键性前提条件，对掌握战场态势具有重要意义[3-4]。

从现有研究来看，旋翼飞机的多普勒回波获取方法可分为实验测量和数值模拟两类。但由于实验测量受外界因素影响较大，难以获取准确的回波[5-6]，因此当前研究更倾向于采用数值模拟方法获取回波[7-11]。

文献[1]最早基于点目标的雷达回波方程，提出了一种旋翼飞机回波求解的积分算法，即将飞机旋翼等效为大量散射点沿轴线均布而成的线条，通过线积分对旋翼飞机回波进行了模拟。文献[2-4]基于此方法，模拟了旋翼飞机不同桨叶数目、形状、转速、姿态角及雷达频率等参数的回波。但上述积分算法人为引入了等效散射点不应存在的微分连续性，忽略了散射点间距存在的客观离散性，获得的回波仅适用于飞机微多普勒特性的定性分析[7]。为此，文献[8-9]对积分算法进行了改进，提出了一种基于散射点等距分布的叠加算法。但是该方法要求各散射点散射系数一致，获得的回波仍然不够准确。为了获得更精确的回波，文献[10]将旋翼等效为若干个散射强度不一的强散射点，进而模拟出旋翼飞机的回波。但文献[11]认为强散射点空间位置会因旋翼转动而发生改变，这种等效强散射点的方法依然无法模拟出真实的回波。

究其原因，以上研究一直局限于将旋翼连续面元用离散散射点代替的思想，同时忽略了飞机旋翼复杂的异形曲面，从而无法模拟出电磁波在旋翼飞机表面的真实散射情况。为此，避开求解旋翼飞机回波的传统思路，从目标高频电磁散射理论出发，提出了基于散射电场的飞机旋翼多普勒回波模拟方法，为后续研究飞机的识别奠定了理论基础。

1 飞机旋翼多普勒回波及其散射点模型

1.1 旋翼多普勒回波的产生机理

旋翼飞机飞行过程中，其机身、主旋翼和尾翼均会对雷达信号的幅度和相位产生一定程度的调制作用，即产生微多普勒现象[1]。这种调制回波包含了用于识别飞机目标的微多普勒特征信息，因此，为准确识别旋翼飞机的目标特征，首要问题是能够准确模拟出飞机的多普勒回波。考虑到旋翼飞机微多普勒特征参量主要由主旋翼产生[7]，因此，仅针对主旋翼的回波进行模拟。

如图1所示，以飞机主旋翼的单桨叶为例，对其多普勒回波的产生机理进行分析。图1中，设桨叶表面某面元dS的运动速度为v，在t1时刻，雷达电磁波波1到达桨叶表面的面元dS，同时雷达发射出波2；在t2时刻，雷达接收到波1产生的回波，此时波2到达桨叶的表面。其中假设桨叶以ω的角速度旋转，t1、t2之间的时间间隔为t′，雷达入射电磁波波速为c、波长为λ，则t2时刻雷达回波的波长为ct′-vt′，从而导致雷达在单位时间内接收到的回波数量不同。

图1 飞机目标对雷达信号的散射示意图

而上述回波接收时间和数量上的差异将导致回波频率的改变，即旋翼产生的微多普勒频移。当桨叶朝雷达电磁波发射方向旋转时，单位时间内雷达接收到的回波数量增加，旋翼回波产生正微多普勒频移；当桨叶背离雷达电磁波发射方向旋转时，则产生负微多普勒频移。旋翼回波的微多普勒频移与雷达电磁波波长、旋翼旋转速度和长度有关[12]。旋翼最大微多普勒频移可以表示为

(1)

式(1)中:frot为旋翼的旋转频率;ω为旋翼的角速度;lb为桨叶的长度。

1.2 旋翼多普勒回波的散射点叠加模型

在现有飞机旋翼多普勒回波的模拟过程中，常采用散射点叠加模型模拟旋翼回波[4]。该模型建立的思想为：取桨叶中心轴线上若干等距的点作为等效散射点，并将桨叶的旋转中心(叶毂)看作单一强散射点，采用点回波方程得到各等效散射点的回波，最后利用矢量叠加的方法模拟出整个旋翼的回波。

如图2所示，设雷达坐标系为M-XYZ，旋翼桨叶坐标系为N-xyz，雷达视线与散射点处于同一平面，即雷达的方位角(α)与俯仰角(β)均为0°，雷达坐标原点与旋翼中心的距离为R0，在(x0，y0，z0=0)处的散射点(Pt0)以恒定的角速度(ω)围绕旋翼的中心旋转，其到旋翼中心距离为lpi，桨叶总长度为l。t0时刻Pt0点初始旋转角为θ0，其与雷达坐标原点的间距为RP(t0)；ti时刻时旋转角为θi，则散射点Pti与雷达坐标原点的间距变为

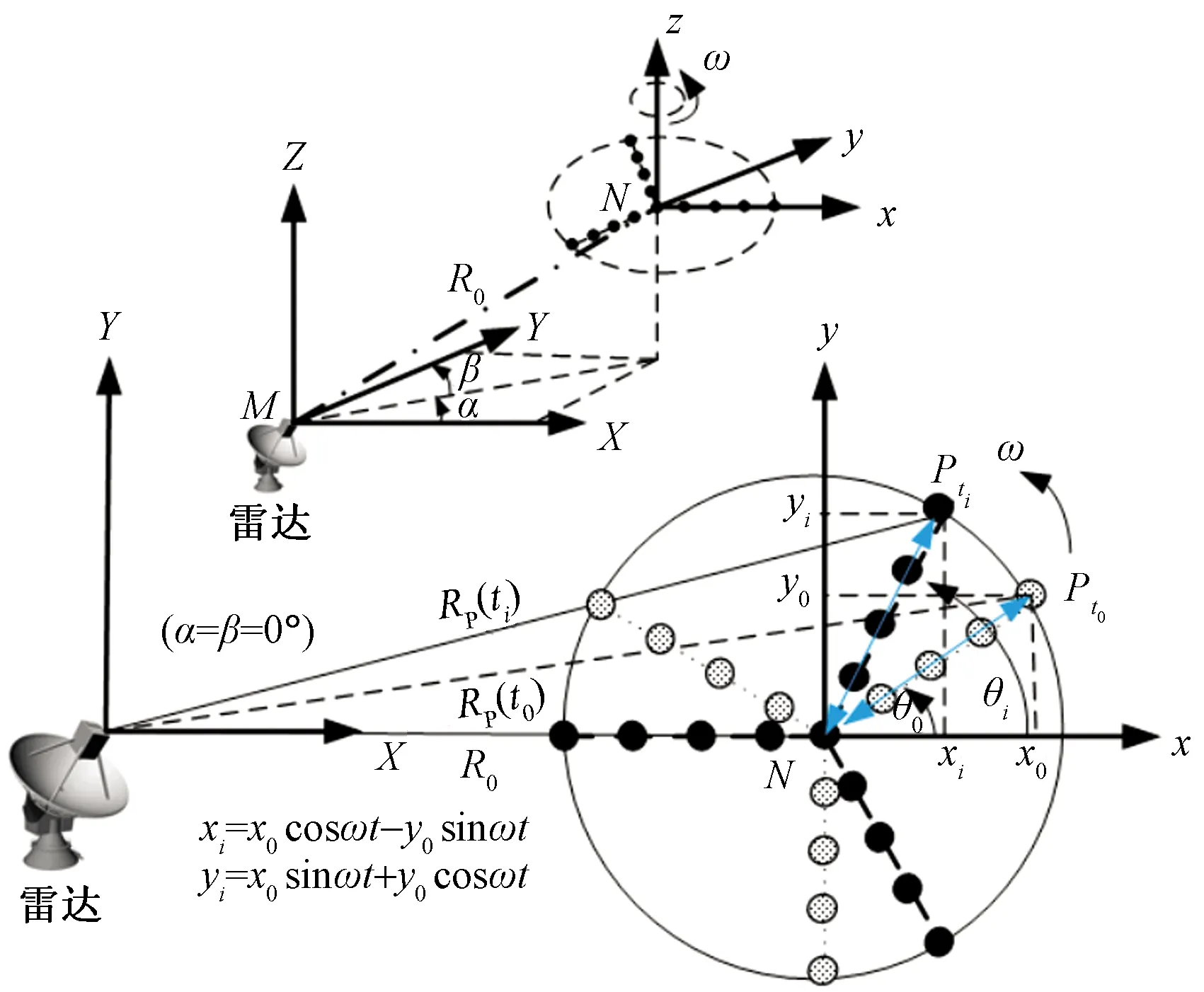
图2 雷达信号与飞机旋翼散射点的几何关系

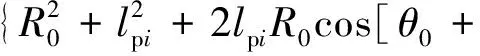
ω(ti-t0)]}1/2

(2)

当雷达发射信号的中心频率为fc、电磁波波长为λ时，则桨叶上任一散射点Pti的回波为

(3)

式(3)中：σi为散射点的后向散射系数，在散射点叠加模型中认为各散射系数相同，散射点之间为等间距；fc为雷达电磁波信号的中心频率。

考虑到单个桨叶包含M个散射点，整个飞机旋翼共含有N个桨叶，将式(3)沿桨叶中心轴线进行离散求和，得到整个旋翼的时域回波表达式为

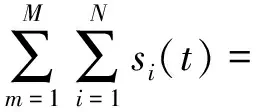
(4)

散射点叠加模型虽然将强散射点的客观离散性进行了考虑，但是默认了相邻散射点之间为等间距分布。同时，在实际工况下，由于飞机旋翼外形结构复杂多样，飞机在飞行过程中姿态不断调整，雷达相对飞机旋翼不同方位角、俯仰角下也会发射不同频率的电磁波，这都将导致旋翼提供的散射区域时刻发生变化。若将这种复杂变化的散射区域用简单的二维散射点模型进行等效，显然无法实现飞机旋翼回波的精确获取。

2 基于散射电场的旋翼多普勒回波模拟方法

2.1 回波方程与散射电场的数学关系

桨叶上任一散射点的回波表达式可变换为

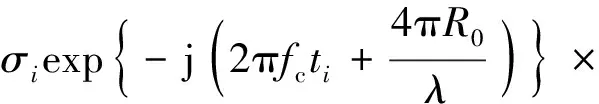
σ(t)exp(-j2πfct)exp[-jΦP(t)]

(5)

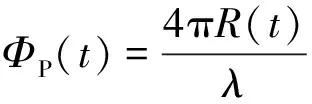
对于呈时谐变化的雷达电磁波信号，时谐场中所产生的散射电场为

Em(r,t)=Em(r)cos[ω′t+φ(r)]

(6)

式(6)中：Em(r)为空间函数，表征散射电场的振幅；ω′为角频率，ω′= 2πfc；φ为电场初相位。

对式(6)提取实部可得

Re({Em(r)exp[jφ(r)]}exp(2πfct)

(7)

式(7)中：Em(r)exp[jφ(r)]为复振幅矢量。

将式(5)和式(7)进行比较可得，散射电场的复振幅矢量与回波方程的基带信号具有一致性，换言之，飞机旋翼的回波信号可通过求解其后向散射电场获得。因此，准确求取飞机旋翼的后向散射电场是模拟其回波的基础。

2.2 基于PO-MoM法的飞机旋翼散射电场求解

现有电磁散射研究过程中，常采用物理光学法(physical optics,PO)求解目标散射电场[13]。但该算法仅考虑了电磁波的直射和折反射情况，即照明区的散射电场，而忽略了电磁波绕射情况，即阴影区的散射电场。由于飞机旋翼尺寸远大于雷达电磁波波长，且其表面形状为复杂的异形曲面，对于桨叶的边缘、叶毂的连接点处等表面不连续位置，若采用PO法等传统高频近似算法则无法对这些区域的散射场进行求解，所求结果的精确性难以得到保证[14]。为此，引入矩量法(methods of moments,MoM)对桨叶阴影区和不连续区域的感应电流进行修正，并与PO法相结合计算出旋翼的总散射电场。

采用物理光学-矩量混合算法(PO-MoM)对飞机旋翼散射电场进行求解时，首先需对旋翼表面求解区域进行划分，将桨叶前缘、叶毂前缘划分为PO区(照明区)，对于PO法无法解决的桨叶后缘及边缘、叶毂后缘和桨叶与叶毂表面连接不连续区域划分为MoM区(阴影区)。其划分示意图如图3所示。

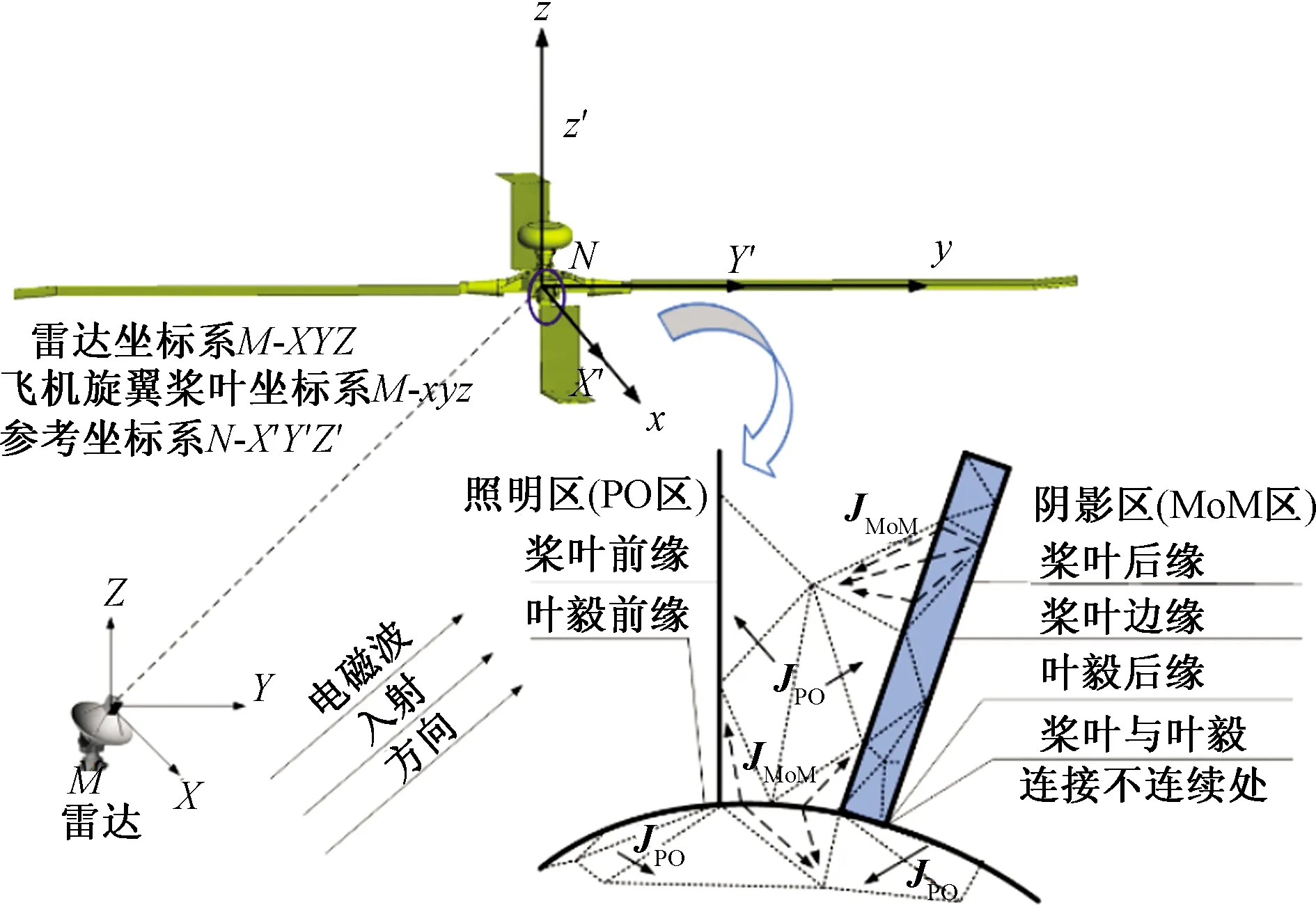
JPO、JMoM分别为PO区和MoM区的感应电流密度

考虑到PO区和MoM区之间的相互耦合及两区域感应电流的连续性，采用RWG(Rao-Wilton-Glisson)基函数对两区域内感应电流密度进行展开，其表达式为

(8)

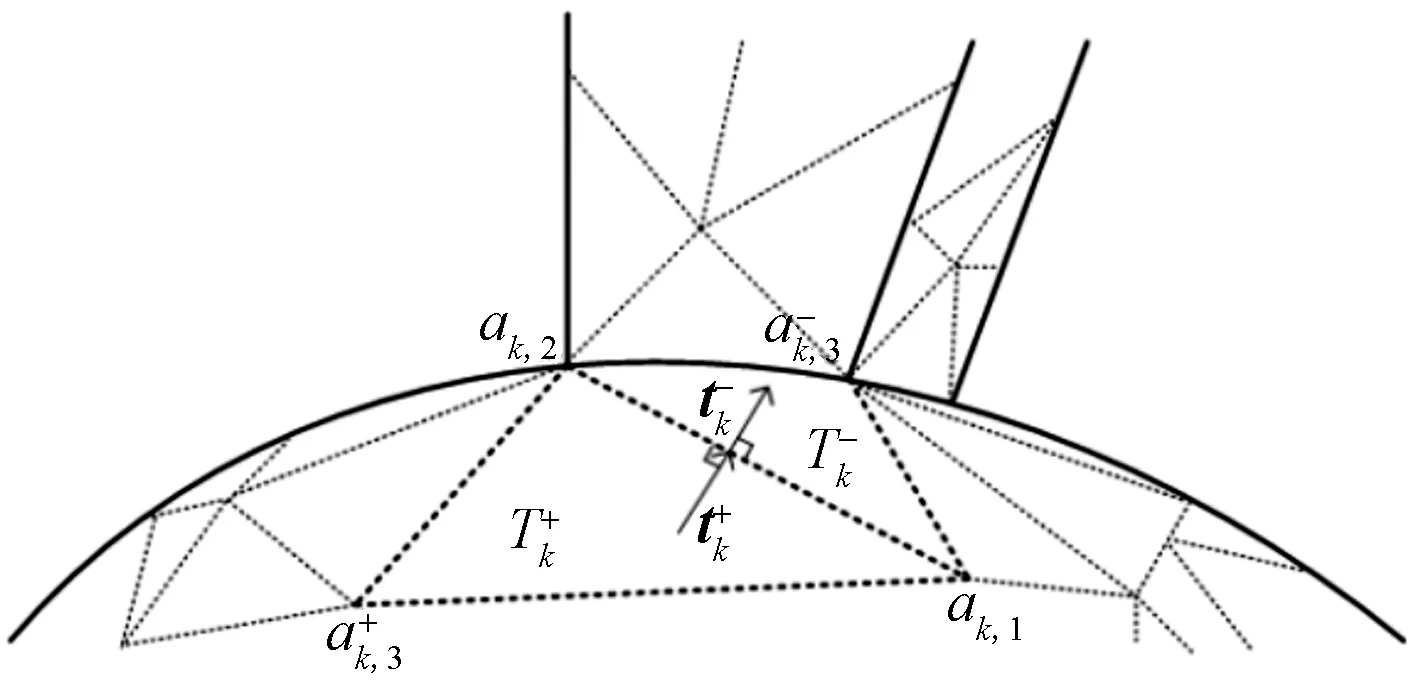
图4 PO区电流分解示意图

(9)

式(9)中:τi,k为入射电磁波对PO区的遮挡系数；αn为展开标量电流系数；τi,n,k为MoM区对PO区的遮挡系数。

在MoM区，结合两区域内感应电流密度，建立该区域下的面电场积分方程为

(10)

式(10)中：LE(·)为电场算子；fn为RWG基函数；Ei为雷达电磁波入射场。

选用伽辽金作测试函数，将面电场积分方程转化为矩阵方程：

(ZMoM-MoM+ZMoM-POτJ,n，k)IMoM=VMoM-ZMoM-POτi，k

(11)

式(11)中:ZMoM-MoM为MoM区内自阻抗矩阵；ZMoM-PO为PO区与MoM区间的互阻抗矩阵；IMoM为MoM区的电流系数矩阵；VMoM为MoM区的激励矩阵。通过上式可求解得到MoM区域下的感应电流，进而可求得旋翼桨叶的散射电场。

2.3 回波模拟步骤

考虑到飞机旋翼在运行过程中处于高速旋转状态，但其转速却远小于光速，符合准静态法的使用条件，即入射电磁波频率远大于目标旋转频率[16]。因此，采用准静态法仿真旋翼的动态旋转过程，通过PO-MoM混合算法计算出第m个时间间隔为Δt下旋翼散射场数据，并不断更新第(m+1)Δt时刻的网格数据，从而得到旋翼旋转一周时间为T的动态散射场序列，最终得到飞机旋翼的回波，其具体的回波模拟过程如图5所示。

图5 旋翼桨叶回波模拟流程图

采用散射电场方法模拟旋翼回波时，首先需要建立旋翼的三维全尺寸模型，然后将旋翼表面离散为若干三角面元，即完成模型的网格剖分。在计算散射电场前，采用欧拉旋转矩阵变换，将旋翼在N-xyz坐标系中的几何数据转化到雷达M-XYZ坐标系中，雷达、旋翼的空间位置如2.2节图3所示。

假设(xr,yr,zr)为坐标系M-XYZ和N-xyz两坐标系原点之间的距离，则旋翼坐标系中的几何数据(x，y，z)变换到雷达坐标系中可表示为

[x1y1z1]T=Rinit[xyz]T+

[xryrzr]T

(12)

式(12)中：Rinit为欧拉旋转矩阵；上标T为矩阵转置。

采用短时傅里叶变换(short time Fourier transform,STFT)对所求的散射电场复振幅矢量数据进行处理，获取得到时频域下的旋翼回波。

3 旋翼多普勒回波模拟方法验证及其对比分析

3.1 回波模拟方法验证

为验证基于散射电场模拟回波方法的正确性，布置如图6所示的金属圆柱体，设置圆柱体在xoy平面内绕坐标原点o做圆周运动。考虑到旋翼桨叶的实际叶长、叶宽和转速，设圆柱体的长度l为7.5 m，半径为0.25 m，旋转角速度ω取40π/3 rad/s，雷达位于x轴上，雷达中心与旋转中心的距离(L)取10 km，雷达中心频率(fc)取5 GHz(C波段)。通过式(1)计算得到叶尖的最大多普勒频移为10.48 kHz，根据Nyquist定律，设定其脉冲重复率30 kHz，采样时间为150 ms。

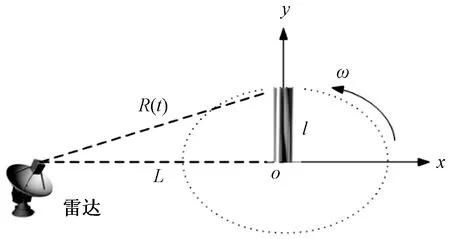
图6 金属圆柱体布置示意图

分别采用1.1节中散射点叠加模型和基于散射电场的回波模拟方法，得到金属圆柱体的时频回波(图7)。由图7可知，两种方法产生的旋转圆柱体时域回波均出现了2个最大峰值，且出现的时刻一致。对于散射电场方法获取的时域回波，在两较大峰值之间还出现了较小波峰。究其原因，可能是由于圆柱旋转过程中，其底面与雷达波束垂直时刻，发生了较大的能量反射。对比图7(a)、图7(b)中的时频回波，均为正弦包络曲线，且两曲线的幅值和周期呈现出较好的一致性，所模拟的回波最大多普勒频移与式(1)计算结果基本吻合，因此基于散射电场的回波模拟方法的正确性得到验证。

图7 旋转圆柱体回波波形

3.2 飞机旋翼回波模拟及其时频对比分析

以AH-64阿帕奇武装直升机为例，建立其旋翼全尺寸几何模型，并对其多普勒回波进行模拟分析，其几何模型如图8所示。该型飞机的桨叶长度为7.32 m，弦长为0.53 m，桨叶最大厚度为0.03 m，桨叶角(δ)为15°，并令与z轴正方向平行的桨叶为第1桨叶，顺时针依次为第2、3、4桨叶，旋转角速度(ω)取40π/3 rad/s，雷达方位角和俯仰角均设置为90°，中心频率(fc)采用5 GHz。

图8 旋翼桨叶几何模型

分别利用散射点叠加模型和本文基于散射电场的回波模拟方法计算，得到如图9所示的AH-64直升机全尺寸旋翼回波波形。对比图9(a)和图9(b)的回波波形可知，两种方法的时域波形的峰值时刻、时频域波形的闪烁时刻和正负多普勒最大频移均出现较好地吻合。因此，基于散射电场的回波模拟方法的正确性再一次得到验证。

图9 旋翼桨叶回波波形

分析图9(a)和图9(b)的回波特征发现，桨叶旋转一周，基于散射电场方法和散射点算法征获得的回波时域特征中均出现了4次相同的峰值，前者时频特征回波图中仅出现了单侧闪烁，而后者时频特征回波却出现了双侧对称闪烁。考虑到桨叶姿态与雷达入射电磁波的相对位置可知，当桨叶叶面与电磁波入射方向垂直时，入射电磁波能量被反射的最多，使得该时刻桨叶散射的能量大于桨叶处于其它姿态的时刻，故在该时刻出现峰值。同时因真实旋翼桨叶的倾斜、扭曲、前后缘厚度的不一致性，导致同一支叶片与电磁波入射方向垂直时，前后两次产生的散射能量存在差异，且有桨叶前缘提供的能量大于后缘，因此出现了图9(b)中正负闪烁差异的现象。而散射点算法出现图9(a)中所示的回波波形，是由于该算法将桨叶模型与散射点近似等效，导致所得的回波波形过于理想。因此通过以上分析可得，采用散射电场方法模拟的回波具有更丰富的细节，更符合真实旋翼的多普勒回波。

3.3 不同桨叶角的多普勒回波对比分析

考虑飞机实际飞行过程中，为了适应不同高度下飞行速度的变化，提高旋翼的工作效率，常采用桨叶角(扭角)可变的旋翼。而桨叶角的改变可能会导致旋翼飞机微多普勒特征回波发生相应的变化。从1.2节可知，传统的散射点积分模型并未将桨叶角这一影响因子进行考虑。因此，分别采用散射点积分模型和基于散射电场的回波模拟方法，对不同桨叶角下的微多普勒特征回波进行具体分析。选取AH-64阿帕奇武装直升机单只桨叶作为基本模型，考虑到实际旋翼桨叶角范围为11.5°～40°，故分别设置桨叶角为15°、30°、45°，桨叶长度、弦长、最大厚度和雷达相关参数仍采用3.2节中的相关设置，得到旋翼桨叶回波波形如图10所示。

从图10(a)～图10(c)可以看出，当其他参数一定时，随着桨叶角度的增大，时频波形中的闪烁次数逐渐由单侧闪烁变化为双侧闪烁，且当桨叶角为45°时，正负微多普勒波形两侧闪烁的能量基本上呈现为对称均匀分布。进一步分析可知，当桨叶角在较小角度时，雷达电磁波照射在桨叶前后缘面积的差值远大于雷达电磁波照射在桨叶面方向上的投影面积，使得同单支叶片与电磁波入射方向垂直时，桨叶前后缘提供的能量起主导作用，导致最终出现单侧闪烁；随着桨叶角的增大，桨叶面在雷达电磁波照射方向上的投影面积逐渐掩盖住了桨叶前后缘厚度的不一致性，使得叶片的电磁波照射面差异逐渐减小，出现正负两侧闪烁，且闪烁能量逐渐趋于对称分布。对比图10(d)所示的回波波形可知，由于散射点积分算法将桨叶模型等效为点、线模型，并无法考虑桨叶角对多普勒回波的影响。因此通过以上可得，采用散射场方法对旋翼回波进行模拟更具有优越性。