基于DPCAALSSVR的燃气轮机负荷估算方法
2021-02-23王开柱焦道顺奚新国周卫庆
王开柱,谭 峰,焦道顺,朱 静,奚新国,孙 魏,周卫庆,薛 锐
(1. 华能南京燃机发电有限公司, 江苏 南京 210034;2. 南京工程学院能源与动力工程学院, 江苏 南京 211167)
随着社会居民消费结构的改变和电力市场的深化改革,电网峰谷差和持续时间都不断增大,用电量呈现的分布规律也日趋复杂,给电网的调度调峰带来了严峻挑战.目前,尽管绝大部分煤电机组已经直接接受电网的AGC负荷指令参与调峰,但电网调峰需求的增长要求更多上网发电机组参与调峰已成为未来不可避免的发展趋势.
燃气-蒸汽联合循环机组具有启停速度快、负荷调节灵活、能源转换效率高等优点,尤其适合于电网调度的调峰任务,而燃机负荷能力的测算是燃机调峰的重要基础.近年来有关燃机负荷分析及调峰调频能力的研究受到了业内的关注,陈淦良[1]从安全性和经济性角度对西门子9F级燃机的调峰能力进行了探究;丁阳俊等[2]建立GE9FA燃机的仿真模型,研究不同负荷与环境温度下的调频能力;王惠杰等[3]则通过历史数据建立了燃机负荷与排温的关联模型;闫顺林等[4]建立了燃机功率对环境温度、压力和湿度的微分模型,利用敏感度因子分析其对负荷的影响程度;黄伟等[5]利用互信息特征选择法得到与燃机负荷相关性较大的变量,进而建立它们与燃机负荷之间的预测模型.有关燃机负荷分析的方法还包括变工况分析、回归拟合、神经网络等[6-11],为燃机调峰的研究奠定了一定基础.动态主元分析(DPCA)是建立在主元分析基础上的变量降维及信息提取技术,适合于提取过程的动态变化信息,而支持向量回归具有良好稳定的预测性能,在动态过程中体现出优越的鲁棒性,两种方法均在不同领域得到了成功的应用与验证.
为适应燃机的动态调峰过程,本文提出了基于DPCA-ALSSVR的燃气轮机负荷实时估计方法,首先利用动态主元分析确定燃机主要参数与负荷之间的相关性程度,通过比较选取与负荷相关性较大的参数,进而利用自适应支持向量机(ALSSVR)构建负荷的实时估计模型,最后通过现场的实际运行数据验证方法的有效性.
1 主元分析及支持向量机
1.1 主元分析及动态主元分析方法
假设某观测的系统有m个变量,每个变量有n个观测值,形成原始数据矩阵X,将其转化为低维的线性无关主元矩阵T,T能够表达X的绝大部分信息,这一转化过程称为主元分析[12],用数学公式描述为:
(1)
SX=Tn×mRm×n
(2)
式中:SX为X的标准化矩阵;R为SX的相关系数矩阵;T=(t1,t2,…,tm)为SX的得分矩阵,有|t1|>|t2|>…>|tm|,t1即为第一主元,表示在该方向投影最大.
取前k个主元,得到:
SX=TkRk+E
(3)
式中:E为残差矩阵;主元Tk=(t1,t2,…,tk)为降维后的新数据.
在传统PCA分析的基础上,动态主元分析方法[12-13]考虑了变量在时序上的动态性影响,对原始数据矩阵X进行扩展,得到的增广阵为:
[X(t)X(t-1) …X(t-s)]
(4)

当计算出滞后因子后,对动态数据矩阵进行标准化处理,根据传统PCA的特征提取步骤确定主元个数,完成动态的主元分析.
1.2 自适应支持向量机
支持向量机是一种以结构风险最小化原则和映射技术为基础的机器学习算法,而最小二乘支持向量机将其中的不等式约束改为等式约束,并将损失函数简化为二次项,实现了优化过程的线性化[14],其数学描述为:
(5)
式中:w为权重向量;b为偏置量;c为惩罚系数;φ(·)为线性映射函数.
通过引入Lagrange函数,利用KKT条件转化为求解线性方程组[15]:
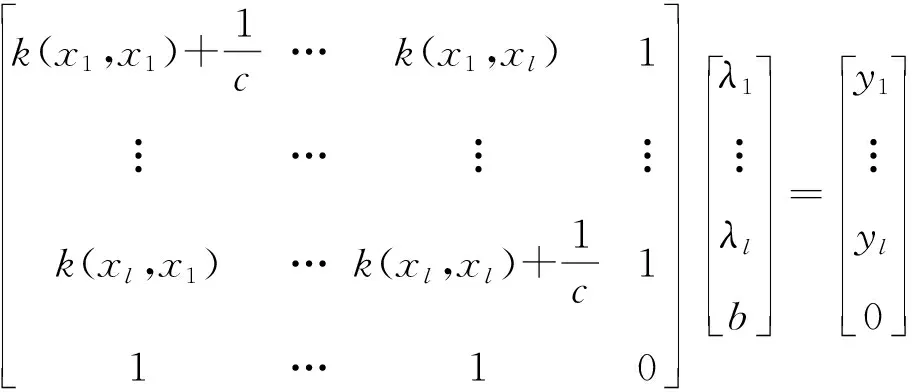
(6)
令
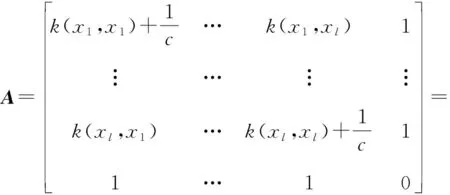
X=[λ1…λlb]T
Y=[y1…yl0]T
核函数为:
k(x,xl)=exp[-‖x-xl‖2/2σ2]
由线性方程组求解得:
(7)
最终确定的LS-SVM模型为:
(8)
由上述可知LS-SVM模型参数包括惩罚系数c和高斯核函数的宽度系数σ,模型的准确性在一定范围内也受其影响,通过优化可获得其最优值.
传统的LS-SVM算法采用离线建模的方式,一旦外界条件变化会导致模型的偏差,本文采用在线自适应更新的方式,增加一个新样本后的K矩阵阶次为:
(9)
式中:β=[K(x1,xl+1)K(x2,xl+1)…K(xl,xl+1)]T;θ=K(xl+1,xl+1)+1/c;Kl和Kl+1分别为原训练样本集和多了一组新样本后的样本集.
对式(9)两边求逆可得:
(10)
式中:e=[0,0,…,0]T;B=-(Kl)-1β;CT=-β-1(Kl)-1;η=θ+CTβ.
在线建模的过程为:首先根据式(9)计算得到β和θ,再利用原始数据集计算得到式(10)中的矩阵B、C和常数η,然后计算得到原始训练数据集K的逆矩阵,最后根据式(7)得到LSSVM的模型参数Lagrange因子λ和偏置量b,最终确定模型的具体形式.
2 实例验证
2.1 数据采集
以国内某E级燃机为研究对象,采集操作员画面上主要参数的历史数据,数据采集遵循两个基本原则:1) 在一段连续的时间内,按照固定的时间周期进行采集,本文选取的采样周期为1 min;2) 数据集覆盖的工况范围应尽可能大,能够包含燃机正常运行的全部区间,工况的参考以负荷为依据.最后合成的数据集可以是几个连续时间段内的子数据集的集合,目的是使得整个数据集覆盖的范围足够广,采集的参数及经过统计后的上下限如表1所示.
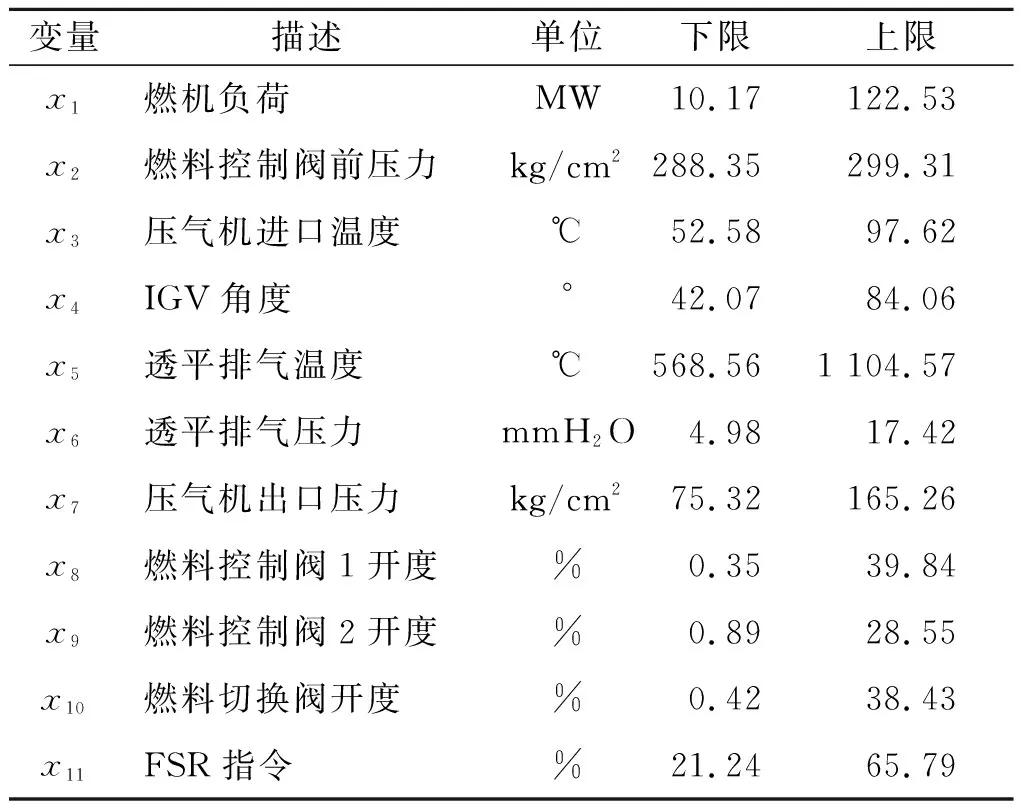
表1 燃机主要参数信息
2.2 参数相关性分析
燃机负荷建模的关键是找到与负荷变动呈现较强关联性的参数集,进而可以利用支持向量算法挖掘它们之间的潜在回归关系,选取一段连续时间段内的历史数据共400组,图1显示了在负荷变动情况下六个主要参数的变化趋势.
从图1中可以看出,燃机的各主要参数随负荷的变化趋势并不一致,从直观上看,FSR指令和压气机出口压力的变化趋势与负荷较为相似,燃料控制阀前压力波动则较为剧烈,其变化趋势与负荷之间并未呈现明显的相关性,而压气机进口温度和燃料控制阀2开度的变化趋势与负荷的相关性则难以从直观上进行简单的定性判断,显然,仅仅依靠人工经验选取建模参数缺乏科学的合理性.
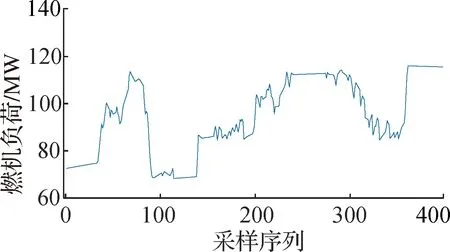
(a) 燃机负荷
本文采用动态主元分析方法求取各参数与负荷之间的相关性,得到一个表示相关性程度的量化指标,称为关联度.选取原始采集数据矩阵X中的负荷和FSR指令两个参数进行关联度计算,得到主元得分矩阵T,其第一主元得分和第二主元得分如图2所示.

(a) 第一主元得分
图2(a)为第一主元得分的变化趋势,第一主元反映了两个参数的主要信息,其变化趋势与参数本身的变化趋势十分相近;图2(b)为第二主元得分的变化趋势,第二主元反映的是参数次要信息,也可以认为是数据中的干扰噪声,其波动特性杂乱无章.通过图2可以得出,两个相关参数之间的变化趋势越相近,其第一主元的变化趋势与其本身变化趋势也越相近.
假设两个参数分别为x1、x2,利用DPCA方法分析得到的主元为T1、T2,其对应的特征值分别为λ1、λ2,则参数之间的关联度表示为:
(11)
从式(11)可以看出,两个参数间的关联度CR介于0和1之间,CR值表示相关性程度的大小,当λ1远大于λ2时,CR的值接近于1,两者间是强相关的状态.图2所示的两个参数(燃机负荷、FSR指令)计算得到的特征值为1.988 7和0.011 3,它们之间的关联度为0.994,两者强相关,图1和图2中的趋势曲线也验证了计算结果的正确性.
根据表1中列出的参数和采集的历史数据,利用DPCA方法对各参数间的关联度进行计算,得到的结果如表2所示.
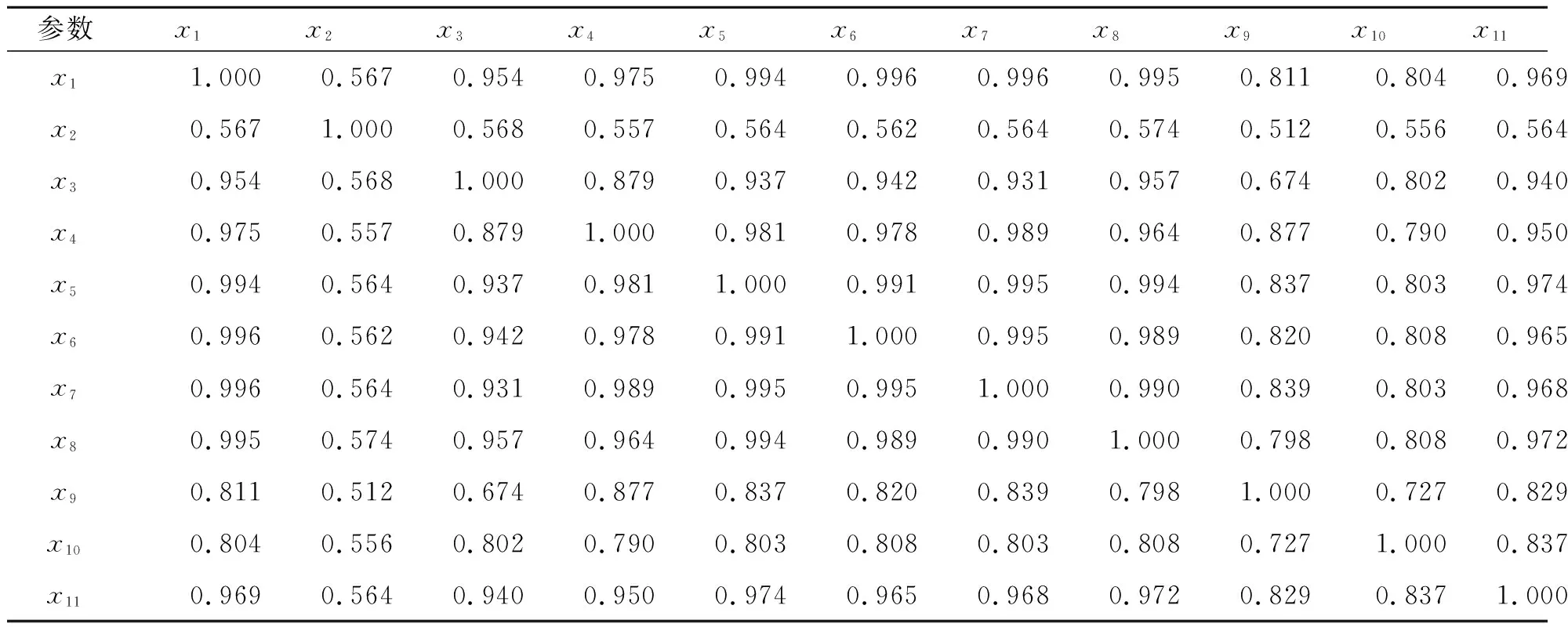
表2 燃机主要参数关联度
表2中的元素表示参数xi与参数xj之间的关联度.表2实际上是一个对称的二维矩阵,对角线上的值均为1,表示参数自相关的关联度为1.其中大部分参数间的关联度较大,而x2(燃料控制阀前压力)与其他参数之间的关联度偏小,属于弱相关特征,x9(燃料控制阀2开度)和x10(燃料切换阀开度)与其他参数的关联度则介于弱相关和强相关之间.显然,基于DPCA的相关性分析方法给出了参数间关联度的量化结果,其计算结果也与图1中各曲线的趋势特征一致.
观察表2中的第一行,以关联度0.9为限,选取与负荷关联度大于0.9的参数作为燃机负荷建模的辅助变量,即x3(压气机进口温度)、x4(IGV角度)、x5(透平排气温度)、x6(透平排气压力)、x7(压气机出口压力)、x8(燃料控制阀1开度)、x11(FSR指令).
2.3 回归建模及参数优化
将采集的400组数据进行划分,其中前200组作为模型的训练样本.后200组作为测试样本,根据确定的输入、输出变量,首先利用训练样本建立燃机负荷的最小二乘支持向量回归模型.最小二乘支持向量回归模型中包含两个可调的参数,它们对模型的准确性有一定的影响.训练的主要任务就是获取最优参数,以此确定最优的回归估计模型.
本文采用交叉验证法对两个模型参数c和σ进行优化,以模型的测试均方差最小化为评判标准.首先划分参数c和σ的取值范围,然后确定两个参数网格的大小,并根据取值范围和网格的大小在整个二维平面内搜索出最优模型的点,此时的点坐标即为最优的模型参数.图3显示了在最优参数附近的部分网格优化结果.
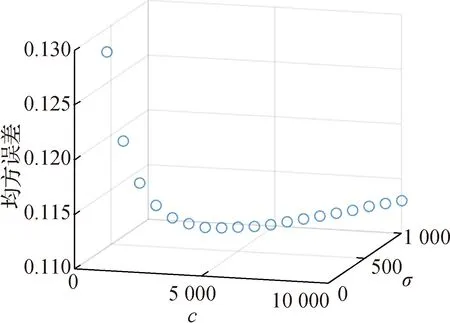
图3 网格交叉验证参数优化
由图3看出,底下的平面是两个参数的优化区间,随着参数的变化,LS-SVM模型测试均方差也在变化,在空间上是一个三维曲线的形状,随着参数的增大,模型均方误差呈现先下降后上升的趋势,当模型误差处于最低点时,参数取得最优值.本次优化的参数最优值取c=5 750,σ=568.
2.4 在线模型验证
根据确定的最佳参数,分别利用最小二乘支持向量机和自适应支持向量机对测试样本进行回归估计,测试的结果如图4所示.
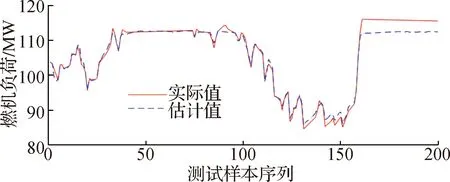
(a) 最小二乘支持向量机
图4(a)和图4(b)分别是最小二乘支持向量机和自适应支持向量机回归估计测试结果,从中可以看出,采用自适应支持向量机方式的估计效果要优于最小二乘支持向量机方式,尤其在样本序列第160—200区间,因为最小二乘支持向量机训练样本中未包含这个区间的高负荷段样本,新样本超出了固有的运行空间,模型的泛化能力受到较大影响,导致计算出现了较大的误差.自适应模型采用在线实时更新的方式,模型能够不断调整扩大运行范围,即使新的样本不在原训练空间内,模型仍然能够及时更新,其回归估计值与实际值吻合度较高,估计效果更好.
3 结语
基于DPCA算法建立了燃机负荷与相关参数的主元分析模型,获得了代表参数间相关性程度大小的量化指标关联度.在此基础上,基于自适应支持向量机建立了燃机负荷的回归估计模型,用于燃机调峰过程中对所带负荷的实时估计和判断.采集某E级燃机的实际历史运行数据,对本文所提方法进行验证,结果表明DPCA关联分析方法能够有效地挖掘出相关变量,基于自适应支持向量回归算法的燃机负荷估计模型具有较高的准确性,其泛化能力优于最小二乘支持向量机建模方式,说明了本文所提方法的正确性和有效性.
