基于目标转换的低复杂度幂次迭代混合预编码算法
2021-02-23吴君钦廖小婷
张 荣, 吴君钦, 王 婷, 廖小婷
(江西理工大学信息工程学院,赣州 341000)
随着当代通信业务需求爆炸式的增长,大规模多输入多输出(multiple-input multiple-output,MIMO)技术使系统收发天线数目得到了数量级的提升,在未来移动通信中起着举足轻重的作用。与此同时,光通信中的毫米波技术也步入了人们的视线。利用毫米波波长短的特性,基站端可以在相同的面积上配备更多天线,从而获得更高的天线增益,实现系统频谱利用率的提高[1]。但毫米波的频率较高,通信过程中存在路径损耗和大气吸收损耗,因此将毫米波技术与大规模MIMO技术结合使用已逐步成为当前通信领域研究的热点内容[2]。对信道进行预编码处理可改善通信的质量,但传统的预编码方案要求发送天线数目与射频链路数目相同[3],若将其直接推广到大规模MIMO通信系统模型中,将导致严重的资源浪费。为节省能耗资源,近年来大量学者投入大规模毫米波MIMO系统预编码方案的设计研究,各种预编码算法陆续被提出。
文献[4]中提出了混合模数预编码的概念,将信道预编码矩阵分为数字和模拟两个模块独立地进行设计。仿真结果表明,混合模数预编码方案可获得比直接编码方案更优的通信性能。文献[5]利用正交匹配追踪(orthogonal matching pursuit,OMP)算法将模拟预编码矩阵的设计问题等效为多元稀疏信号的重构问题,算法性能较好,但该算法需要构建候选矢量集,每次迭代都需从矢量集中寻找出一个最优矢量,计算复杂度高。针对该问题,文献[6]提出了无需设计候选矢量集合的混合预编码算法,计算复杂度低,但算法是基于全连接架构模型,导致所需天线数目和移相器数目远远超过部分连接架构模型,成本代价高;文献[7]中提出了衡量毫米波MIMO系统性能的新标准——系统总可达速率R,R的取值越大,通信系统的频带利用率越高;文献[8]中,以总可达速率R最大化为目标,提出了一种基于连续干扰消除(successive interference cancellation,SIC)的部分连接混合预编码算法,该算法要求输入系统的数据流数等于射频链路数,在很多情形下会损失一定的系统性能;文献[9]提出了一种基于等效信道增益的混合预编码算法JI-SIC,该方案不再要求输入系统的数据流数等于射频链路数,但因其基于奇异值分解(singular value decomposition,SVD)涉及大量高维度矩阵运算,计算复杂度高;文献[10]提出了一种几何均值预编码算法,该算法不需进行SVD分解就可以获得较好的性能,但对通信环境要求较高。文献[11]打破了对通信环境的限制,将信道转换成多个子信道进行通信,但只适用于单用户系统,在实际应用中存在极大的局限性。
为了解决上述文献所提方案中成本高、复杂度高、性能良、适用范围小等不足,提出了一种基于目标分解的低复杂度幂次迭代混合编码算法。该算法以获得系统最大总可达率为前提,采用部分连接架构模型,在确保系统性能的条件下,降低了成本;利用矩阵分割、迭代算法、数学归纳法降低编码方案计算复杂度,节省能耗;不再要求数据流数目等于射频链路数,适用范围更广。相对于现有的其他算法,所提算法对通信系统的性能、能耗和适用性进行了很好的均衡。
1 系统模型
1.1 传输模型
大规模毫米波(millimeter wave,mmWave)MIMO下行链路信道传输模型具有两种架构[5]:全连接型和部分连接型。图1所示为全连接型架构模型,其中每根发送天线与一个相加器、K个模拟移相器、K条射频链路(RF链)相连接[6]。当基站端配备MN根天线时,一共需要MN个相加器、KMN个模拟移相器、KMN条射频链路。图2所示为部分连接架构模型,图中每条射频链路仅通过M个模拟移相器和M根天线发射信号。当基站端配备MN根天线时,一共需要个MN个模拟移相器、N条射频链路。在部分连接架构模型中,整个通信过程不再需要相加器的参与,并且所需天线和射频链路数量较少,具有成本低、节能的优点,这些优势使得部分连接架构模型适用范围更广泛[1,5-6]。
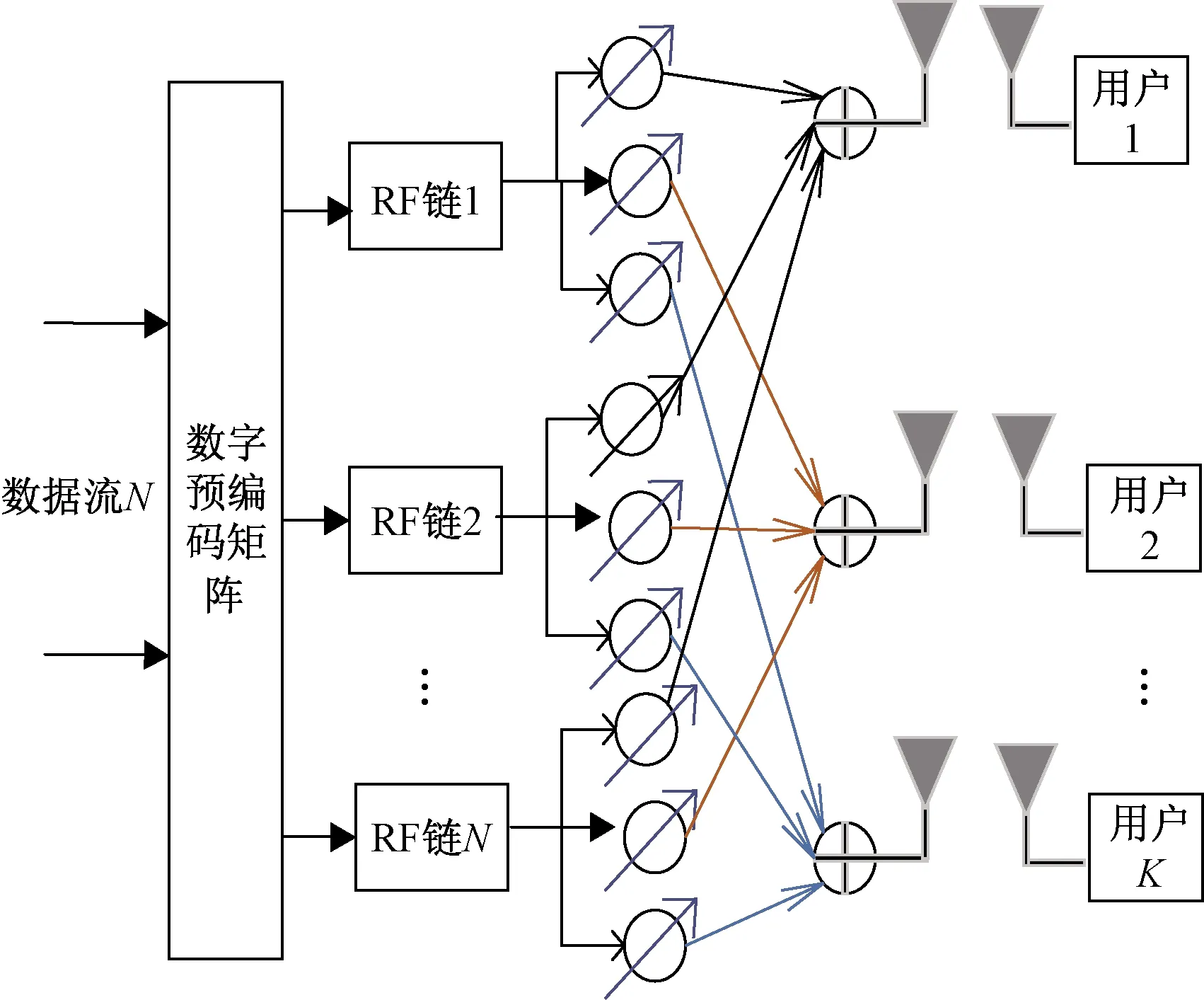
图1 全连接架构模型

图2 部分连接架构模型
在多用户大规模mmWave MIMO通信系统中,基站端利用毫米波频率高波长短的特性,可在相同的面积上配备大量天线,结合空分复用技术可实现系统增益的大幅增加[1,2,6-10],且通信系统模型中用户端接收设备简单[12],结合以上两点,用户接收信号可以直接视为基站端天线的发送信号。用户接收信号y可以表示为
y=ρHPs+n
(1)
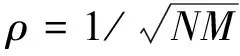
在图2所示的部分连接架构模型中,混合模数预编码矩阵P划分为数字预编码矩阵D和模拟预编码矩阵A两个模块分别独立地进行设计,即P=AD。其中数字预编码矩阵实现功率的分配,其值可变,模拟预编矩阵仅用于相位大小的调整,其模值不可改变[12]。系统总可达速率R可表示为
(2)
1.2 信道模型
在毫米波通信系统的传输环境中有着少量散射体的存在,传统的瑞利衰落信道模型中没有考虑散射体的存在,而低频通信模型中散射体的数量丰富[13],因此采用几何信道模型[8-11],信道中存在的散射体数目记为S,信道矩阵H可表示为
(3)
式(3)中:Arx(θ)、Atx(θ)分别为接收阵列响应矩阵、发射阵列响应矩阵;θi∈[0,2π]为第i条路径的到达角;φi∈[0,2π]为第i条路径的发射角;G表示路径增益,服从正态分布。使用均匀线性阵列(uniform linear array,ULA),阵列发射矢量、响应矢量进行归一化后可分别表示为
(4)
式(4)中:λ表示信号波长;d表示天线间距。
2 基于目标转换的低复杂度迭代混合预编码算法
2.1 设计过程中的目标转换
以获取系统最大总可达率R为目标,对混合模数预编码矩阵P进行设计。为降低算法复杂度,数字部分的预编码矩阵D可定义为一个对角阵[10],即D=diag[d1,d2,…,dNS]。对图2所示的部分连接架构模型进行模拟预编码时,每条射频链路仅与M个移相器相连接,则模拟预编码矩阵A可表示为
(5)
P=AD=
(6)
利用矩阵可分割性,将矩阵P分割为前NS-1项和第NS项,即P=[PNS-1,PNS],PNS∈CNM×1,PNS-1∈CNM×(NS-1),故式(2)可表示为

log2(|TNS-1IK|)+
(7)
log2(|TNS-1IK|)=log2(|TNS-1|)=
log2(|TNS-2|)+
(8)

R=R1+…+RNS=
(9)
根据式(9),可将系统总可达率R的优化问题转换为式(10)中预编码矩阵P的第n个矢量Pn∈CMN×1的优化问题,其中1≤n≤NS。
(10)
因子天线阵列中仅使用了M根天线,故矢量Pn和等效信道矩阵Gn-1可表示为
(11)
Gn-1=RHHTn-1-1HRH
(12)

(13)
式(13)中:Gn-1为Hermitian矩阵,具有以下两个性质:①Gn-1为对角阵;②Gn-1右奇异值与特征值相同,右奇异向量与特征向量相同。
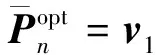
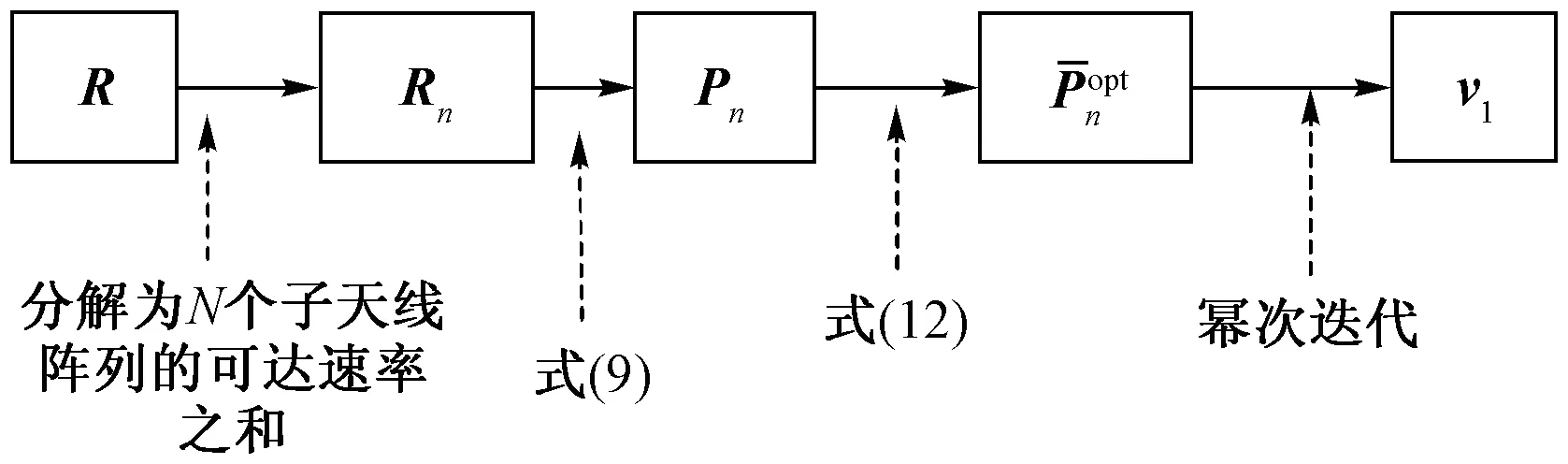
图3 算法目标转换流程图
2.2 混合预编码矩阵P的设计
通过低复杂度的幂次迭代算法获取Gn-1的第1个右奇异向量v1,避免了文献[9]提出的JI-SIC算法中涉及到的大量高维度矩阵求逆问题,具体步骤如下。
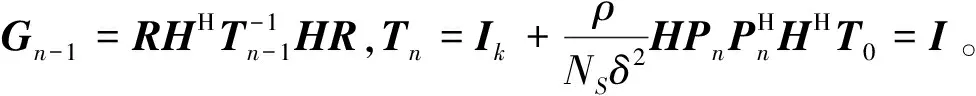
2.3.2 脉冲声辐射力成像 (acoustic radiation force impulse imaging,ARFI)脉冲声辐射力成像是通过超声给组织施加局部辐射力,利用声辐射力的聚焦,在特定的线上产生推力,组织受到推力产生相应的应变,然后突然停止声辐射力,在应变恢复过程中检测不同时间点的应变情况,从而反映组织的黏弹特性。由于ARFI是采用声能机械性激励的方式,依然是通过位移来估算形变,所以本质上是应变成像。
(14)

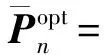
(15)
由式(15)可知
(16)
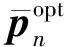
综上所述,提出的低复杂度混合预编码算法可描述为以下几个步骤。
步骤1输入T0=I,u(0)=[1,…,1]T,并对幂次迭代算法的迭代次数S赋初值。

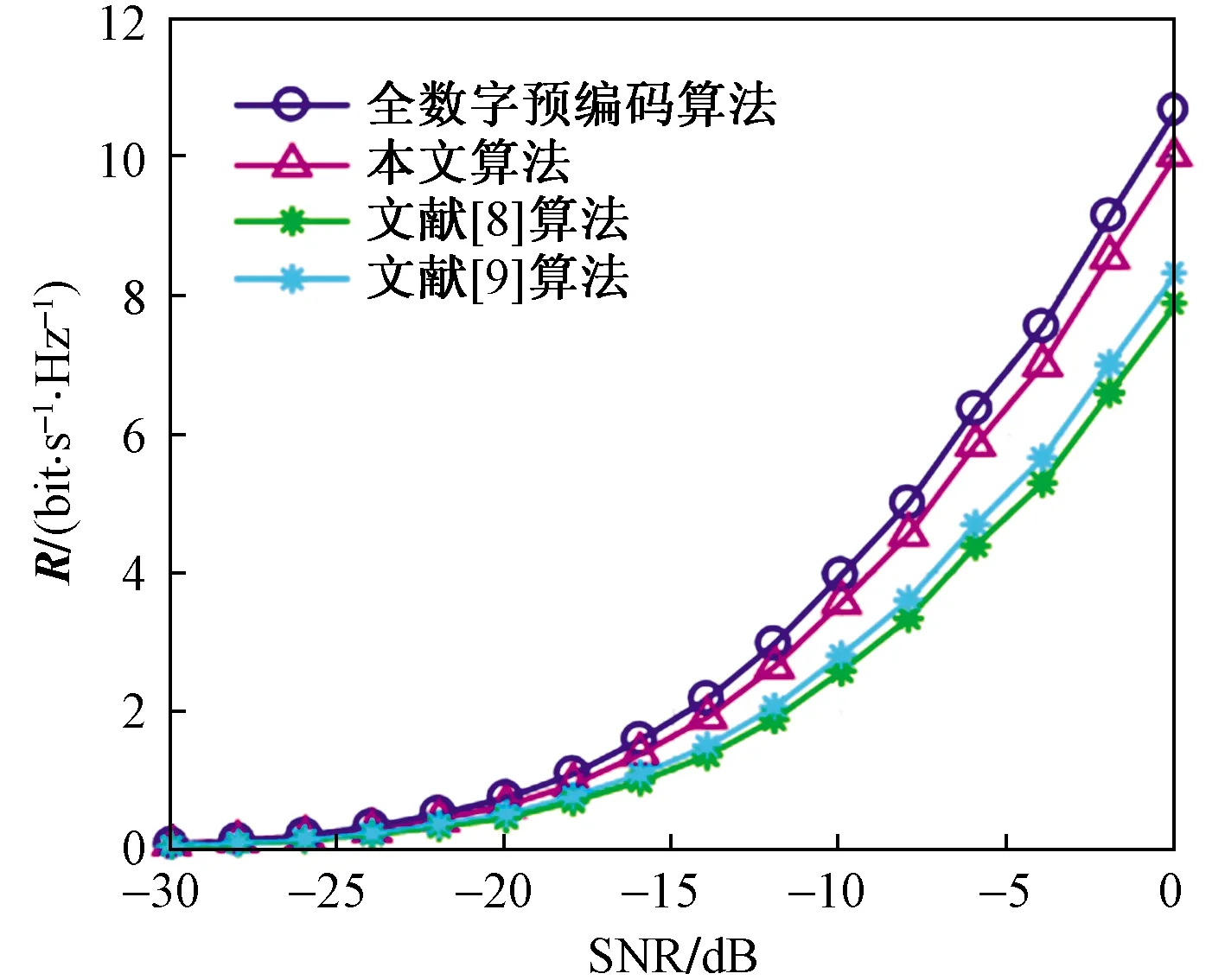
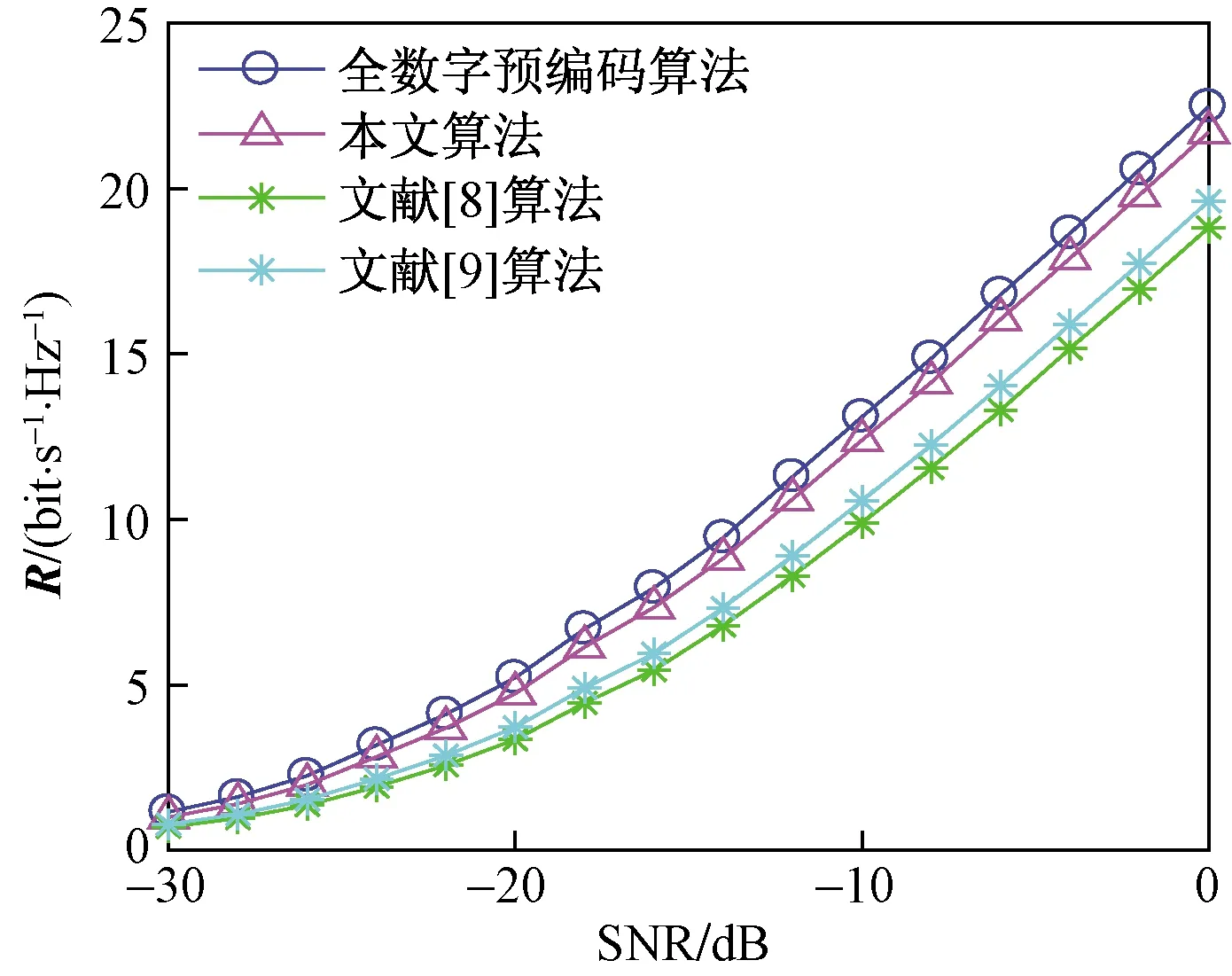
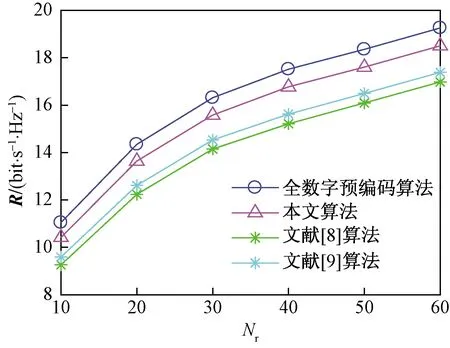
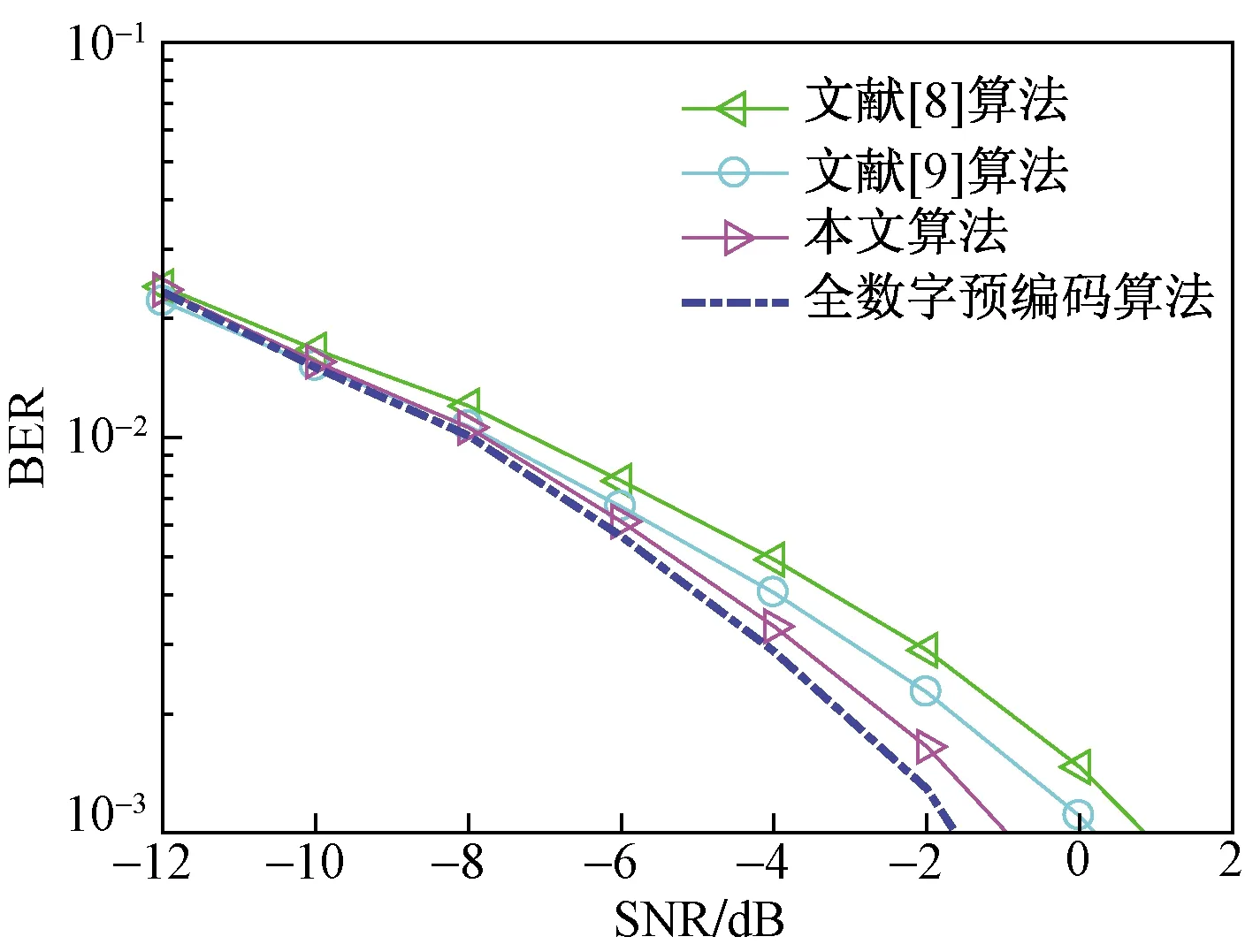
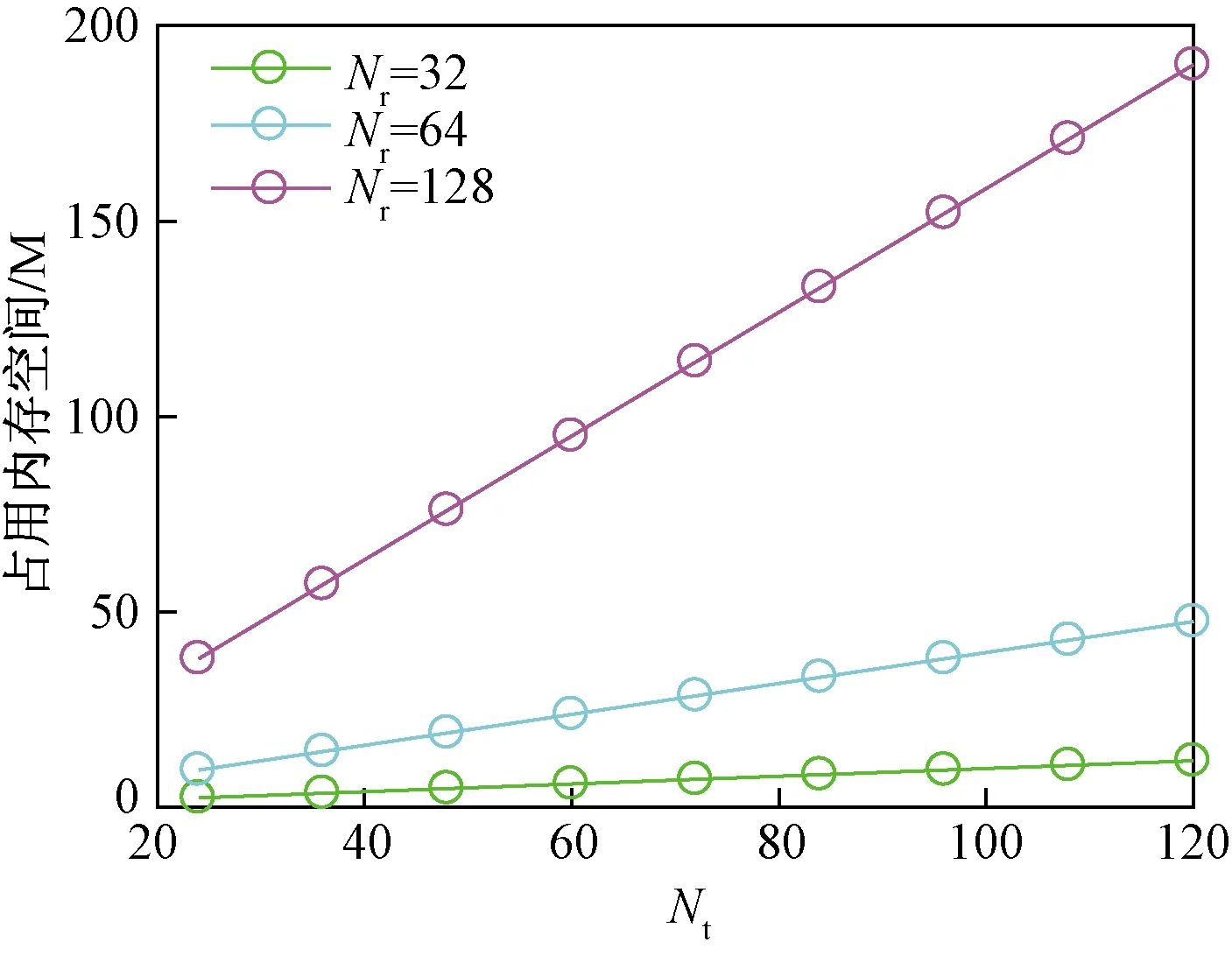
步骤3利用Aitken加速算法,加快步骤2中幂次迭代收敛。当1≤s≤2时,n(s)=m(s),当2 步骤4计算u(s)=Z(s)/n(s),对前一个u(s)进行更新,然后返回步骤3,直到s大于S时结束循环。 仿真环境采用大规模毫米波几何信道模型,载波频率为28 000 MHz,有效路径L=3,发射端和接收端均采用均匀线性天线阵列(ULA)。基站端天线全向发送信号,发送角在区间[0,2π]上服从均匀分布,用户端天线全向对信号进行接收,到达角在区间[0,2π]服从均匀分布。基站端天线间的间距d=λ/2,其中λ是信号的波长。为验证所提编码算法的有效性和可靠性,将其从系统总可达率和误码率两个维度分别与全数字预编码算法、文献[8]提出的基于SIC模数预编码算法、文献[9]中提出的JI-SIC预编码算法进行了比较。 图4所示为在毫米波通信环境下,系统参量Nt=64,Nr=16,NRF=8时,以上4种算法在相同信噪比(SNR)下的性能曲线图。由图4可得,随着输入信噪比的增大,通过预编码的方式均可实现系统通信性能的改善。编码方案越好,则系统的总可达率越高、性能曲线增长越快。显然,本文算法的系统性能优于文献[8]、文献[9]中的算法。 图4 信道参量为Nt=64,Nr=16,NRF=8且信噪比相同时,不同算法性能曲线 图5所示为在毫米波通信环境下,系统参量Nt=256、Nr=64、NRF=32时,各算法在相同信噪比(SNR)下的性能曲线。由5图可得,随着收发天线数目的增多,本文算法可获得比文献[8]、文献[9]中算法更高的系统增益,有效性更高。 图5 信道参量为Nt=256,Nr=64,NRF=32且信噪比相同时,不同算法性能曲线 通过图4和图5可得,当每条射频链路连接的天线数目M保持不变,增加射频链路NRF数目和接收天线Nr数目时,发送天线数目Nt=MNRF增大,且各算法的系统总可达率均得到明显地提升。 图6所示为各算法中接收天线数目与系统总可达率的关系。由图6可得,随着接收天线数目的增多,所有预编码算法都使通信性能都得到了改善。在接收天线数目相同条件下,本文算法的系统总可达率高于文献[8]、文献[9]中的算法的系统总可达率,逼近最优全数字预编码算法的系统总可达率,具有很好的有效性。此外,发现本文算法中Nr=60的点与全数字编码算法在Nr=50的点具有相同的总可达率,这说明了通过增加少量的用户接收天线就可以弥补本文算法因基于部分连接结构导致的性能损失,因此文中所提算法在大规模毫米波MIMO通信中具有很好的适用性。 图6 各算法中接收端的天线数目与系统总可达率关系图 图7所示为各算法中输入信噪比与系统误码率的关系图。由图7可得,各预编码算法的系统误码率随着输入信噪比的增大而减小。在相同输入信噪比的条件下,本文算法的系统误码率低于文献[8]、文献[9]中的算法,接近全数字预编码算法,具有很好的可靠性。 图7 各算法输入信噪比与系统误码率的关系图 对基于目标转换的迭代混合预编码算法的计算复杂度进行了分析,并同文献[8]、文献[9]中两种预编码算法的复杂度进行比较。本文算法的计算复杂度由以下几个部分组成。 (1)由步骤1获取Gn-1初值时,n=1,T0=I,G0=RHHHRH,RHH∈CM×K,HRH∈CK×M,由矩阵性质可得该部分存在KM2次乘法,0次除法。 (2)步骤2中共进行S次循环,循环体中Z(s)的每次更新有M2次乘法,Z(s)=Gn-1u(s-1)。 (3)步骤3 Aitken加速算法通分后需要两次乘法,一次除法。 (4)Ti进行更新时一共进行N次划分,结合(2)得共需NM2次乘法和N次除法。 综上所述,基于迭代的混合模数预编码算法约需M2(NS+K)次乘法、2SN次除法,计算复杂度为ο[M2(NS+K)+2NS]。文献[8]中提出的基于连续干扰消除的混合预编码方案计算复杂度为ο(M3N+KMN3),文献[9]中提出JI-SIC算法的复杂度为ο(KNSM2N2+M3N3)。 图8所示为系统变量为M=4,K=16,NRF=16,S=200时,各编码算法发送天线数目与迭代次数的关系。由图8可得,随着天线数目的增多,预编码算法对数据的处理变得更加复杂,各编码算法的复杂度均呈现增长趋势。预编码算法方案越好,曲线增长越缓慢,需要迭代的次数就越少。显然,本文算法复杂度远小于文献[8]、文献[9]中算法的计算复杂度,具有更好的有效性。 图8 M=4、K=16、NRF=16、S=200时,发送天线数与算法迭代次数关系 对基于目标转换的迭代混合预编码算法的空间复杂度进行分析,并给出不同规模运算下辅助变量占用的内存。算法的空间复杂度是由程序代码所占空间、输入数据所占空间、辅助变量所占空间3个部分组成。不同算法解决同一问题时,各个算法在运算过程中生成的辅助变量所占用的内存决定其空间复杂度。因此,本文算法的空间复杂度主要由以下几个部分组成。 (1)由步骤1中T0的初值,创建M×M维的辅助空间矩阵Gn-1。 (2)步骤2利用矩阵Gn-1和矢量u(n-1),创建M×1维的辅助矢量Z(s),并选取Z(s)矢量中最大的元素m(s)。 (3)步骤3利用Aitken加速算法创建空间用于存储奇异值变量n(s)。 (4)步骤4中利用变量n(s),创建M×1维的辅助矢量u(s)。步骤3和步骤4一共循环S次。 (5)步骤5结合u(s)创建M×1维辅助矢量v1。 Ti进行更新时一共进行N次划分,即产生了N个Nr×Nr的辅助矩阵Tn。 图9所示为系统变量M=6、S=5时,本文算法在不同规模收发天线中所占用的内存图。由图9可得,算法占用内存大小与收发天线的规模呈正相关。当接收天线数目Nr相同时,本文算法占用的内存随着发送天线数目Nt的增加而缓慢增大。当发送天线数目Nt保持不变时,本文算法占用的内存随着接收天线数目Nr的增加而急剧增大。因此,接收天线规模的大小对本文算法占用的内存起着关键性作用。在实际生活中使用的MIMO技术规模为64×64,即收发天线的数目均为64根,此时本文算法生成的辅助变量占用的内存不足50 M,占用内存小。在未来大规模MIMO场景下,本文算法可通过增加大量发送天线,达到以较小内存获得更大的系统增益的目的。 图9 M=6、S=5时,本文算法在不同规模下占用的内存 提出了一种基于目标转换的低复杂度迭代混合预编码算法。以获得系统最大总可达率为目标,对混合预编码矩阵进行分解设计。在获取矩阵右奇异矢量的过程中,利用幂次迭代算法替换传统的SVD分解算法,并在迭代过程中加入Aitken算法加速迭代,在保证系统通信性能的条件下大幅度地降低了计算复杂度。此外,本文算法不再要求输入数据流数等于射频链路数,打破了文献[8]中所提算法的局限性,适用范围更宽泛。仿真结果表明,本文算法比文献[8]、文献[9]中提出的算法具有更高的有效性和可靠性,且性能上逼近全数字预编码算法。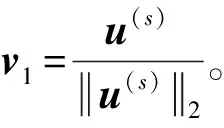
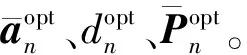
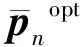
3 算法仿真与复杂度分析
3.1 算法仿真分析
3.2 计算复杂度分析

3.3 空间复杂度分析
4 结论
