北斗二号系统非核心区域定位精度影响因素分析

侯 睿,郭金运,周茂盛,刘 新,纪 兵,刘智敏

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.海军工程大学 导航工程系，湖北 武汉 430033)

中国北斗二号系统的建成和使用极大促进了中国导航定位事业的发展，北斗二号系统的研究和应用前景已经变得越来越广阔。目前，北斗二号系统主要服务于亚太地区，其服务的重点区域为东经55°～180°，南北纬55°之间[1]。

近年来，国内外学者开展了大量关于北斗二号系统定位精度影响因素的研究。Liu等[2]利用北斗区域导航系统，完成了北斗高精度定位任务，并对北斗解算方案中的参考站选择、站间距离等因素进行了研究。李森等[3]将北斗卫星系统应用于高精度工程控制测量，将北斗系统定位精度与全球定位系统(global positioning system，GPS)系统进行比较，认为可以将北斗系统应用在厘米级定位精度的测绘领域，并探讨了北斗系统精密星历对解算北斗数据的影响。吴仁攀等[4]利用天津、武汉和广东连续运行参考站(continuously operating reference stations，CORS站)网内的实测北斗卫星数据进行了北斗相对定位精度影响因素的研究。目前北斗二号系统的研究和应用区域主要局限于北斗二号系统服务的核心区域，对于非核心区域(服务区域55°E～180°E，55°S～55°N之外的区域)研究较少。因此，研究北斗二号系统非核心区域定位精度的影响因素，并针对这些影响因素制定最佳的数据处理策略对提高北斗二号系统在非核心区域的定位精度具有非常重要的意义。

为了探讨北斗二号系统非核心区域相对定位精度的影响因素。本研究将对精密星历和基线解算策略中4个参数(观测量选择、卫星高度截止角、干湿映射函数、对流层天顶延迟估计时间间隔)进行研究。探究这些因素对北斗二号系统非核心区域相对定位精度的影响，并根据这些影响因素给出最佳的北斗二号系统非核心区域数据解算策略。

1 数据及方法

1.1 研究区域和数据

为针对北斗二号系统非核心区域进行研究，选取20°W～180°W, 70°N～60°S作为研究区，主要包含美洲和东太平洋地区。

MGEX(Multi_global navigation satellite system(GNSS)experiment,多全球导航定位系统实验项目)2012 年由国际GNSS服务组织(International GNSS service,IGS)工作组提出[5-7]。研究数据取自MGEX机构，包括北斗导航星历(https://igs.bkg.bund.de/root_ftp/IGS/BRDC/)[8]，混合观测数据(ftp://igs.ign.fr/pub/igs/data/)[9]和混合精密星历(ftp://cddis.gsfc.nasa.gov/gnss/products/mgex/)[10]。共选取17个IGS站的观测数据作为实验数据，数据采样间隔为30 s，站点主要位于美洲地区和东太平洋地区，海陆及中高低纬度皆有分布，测站站点分布如图1所示。

图1 测站站点分布

1.2 研究方法

GAMIT作为一款高精度全球导航定位系统(GNSS)数据处理软件，由于其优良的解算精度，在国内外高精度GNSS数据处理中得到了广泛应用[11-12]。目前GAMIT可以进行北斗二号卫星系统数据的解算，因此采用GAMIT10.7作为北斗二号系统数据解算软件。

为了研究北斗二号系统在非核心区域的相对定位精度，将对17个IGS站数据设计5种实验策略。由于观测数据同时包含GPS数据和北斗二号系统数据，因此将相同测站同时段的GPS单天解作为参考值，GPS解算使用IGS精密星历，基线解算策略及参数设置如表1所示。

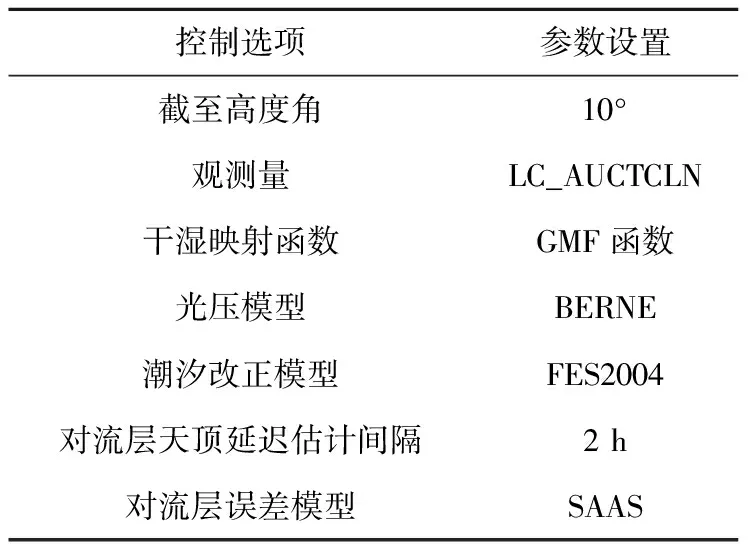
表1 基线解算策略

方案1，研究不同精密星历对北斗二号系统在非核心区域相对定位精度的影响。分别使用欧洲定轨中心(centre for orbit determination in Europe，CODE)、德国地学中心(geo forschungs zentrum，GFZ)和武汉大学(Wuhan university，WUM)三个分析中心提供的精密星历进行北斗二号系统数据解算，每组连续解算20天(2018年年积日007至026)，基线解算策略如表1所示。

方案2，研究解算策略参数中干湿映射函数参数对北斗二号系统在非核心区域定位精度的影响。分别使用3种干湿映射函数NMF(niell mapping function)、VMF1(vienna mapping functions 1)、GMF(global mapping function)进行北斗二号系统数据解算，共解算7天(2018年年积日020至026)，精密星历使用CODE精密星历，除干湿映射函数之外的其他基线解算策略采用表1中的参数。

方案3，研究解算策略中观测量选择参数对北斗二号系统在非核心区域定位精度的影响。分别采用基于伪距解算宽巷模糊度和利用电离层约束求解宽巷模糊度进行北斗二号系统数据解算，共解算7天(2018年年积日020至026)，精密星历使用CODE精密星历，除观测量选择之外其他基线解算策略采用表1参数。

方案4，研究解算策略中卫星高度截止角对北斗二号系统在非核心区域定位精度的影响。对北斗二号系统数据进行解算，将卫星高度截止角分别设置为0°、5°、10°、11°、12°、13°、14°、15°、20°、25°、30°、35°、40°，共解算7天(2018年年积日020至026)，使用CODE精密星历，除卫星高度截止角之外的其他解算策略采用表1中的参数。

方案5，研究解算策略中对流层天顶延迟估计时间间隔对北斗二号系统在非核心区域定位精度的影响。对北斗二号系统数据进行解算，将对流层天顶延迟估计时间间隔分别设置为每1 h解算一次、每2 h解算一次、每4 h解算一次，共解算7天(2018年年积日020至026)，运用CODE精密星历，除对流层天顶延迟估计时间间隔之外的其他解算策略采用表1中的参数。

2 结果和分析

2.1 不同精密星历对北斗二号系统在非核心区域定位精度的影响

为了分析不同精密星历对北斗二号系统在非核心区域定位精度的影响，分别使用CODE、GFZ、WUM三家机构发布的精密星历进行北斗数据解算，并将单天解中的北斗解算结果与GPS解算结果进行对比，统计测站北斗解算与GPS解算在N、E、U三方向上差值的最大值(MAX)、最小值(MIN)、平均值(MEAN)和标准差(STD)，统计结果如表2所示，并根据(1)式分析测站的标准差，统计结果如图2所示。

表2 不同精密星历解算精度统计

(1)

其中：STD总为点位误差，STDN为N方向标准差，STDE为E方向标准差，STDU为U方向标准差。

由表2知，在北斗非核心区域测站单天GPS解算值与北斗解算值的差值中，最大值达到米级，平均值达到厘米级，标准差精度达到分米级。由图2知，最优结果(点位误差最小)中76.4%使用CODE精密星历解算；最优解算结果中11.8%使用WUM精密星历解算；最优解算结果中11.8%使用GFZ精密星历解算。通过比较发现，使用CODE精密星历进行北斗二号系统数据解算的精度和稳定性较高，WUM次之，GFZ精度稍差，因此在非核心区进行北斗二号系统数据解算时建议使用CODE精密星历。

图2 不同精密星历测站点位标准差统计

2.2 干湿映射函数对北斗二号系统在非核心区域定位精度的影响

映射函数是对流层延迟改正中的重要组成部分，是将天顶方向延迟量准确转化为信号传播路径方向的关键。选择一个合适的映射函数对于提高数据处理精度具有十分重要的意义[13-14]。

表3为方案2中分别利用三种映射函数进行解算的精度统计表，通过统计发现，三种模型的测站单天GPS解算值与北斗解算值的差值中，最大值达到米级，平均值在厘米级，标准差在分米级。对三组实验分别以测站为单位绘制点位误差图，由图3知最优结果(点位误差最小)中的53%使用NMF函数；最优解算结果中的17.6%使用VMF1函数；最优解算结果中29.4%使用GMF函数。经过比较发现，VMF1函数精度和稳定性稍差，GMF函数次之，NMF函数精度和稳定性较好，因此在非核心区进行北斗二号系统数据处理时建议使用NMF映射函数。

表3 不同干湿映射函数解算精度统计

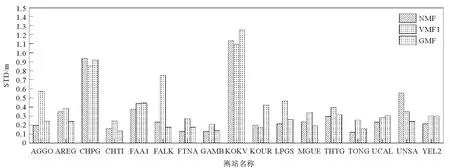
图3 不同映射函数测站点位标准差统计

2.3 不同观测量选择对北斗二号系统在非核心区域数据处理定位精度的影响

GAMIT软件在采用双差载波相位观测值解算长基线时提供了两种解算模式：一种是基于伪距解算宽巷模糊度; 另一种是利用电离层约束求解宽巷模糊度。由于基于伪距解算宽巷模糊度和利用电离层约束求解宽巷模糊度均为基于无电离层组合载波相位观测值，区别仅在于如何分解LC整周模糊度，地球不同区域电离层分布将会影响长基线解收敛速度和LC 模糊度分解精度[15]，因此观测量选择对于提高数据处理精度具有十分重要的意义。

表4为方案3分别使用基于伪距解算宽巷模糊度和利用电离层约束求解宽巷模糊度作为观测量进行解算的精度统计。结果表明分别使用两种不同观测量时，测站单天GPS解算值与北斗解算值的差值中，最大值达到米级，平均值为厘米级，标准差为分米级。对三组实验分别以测站为单位绘制点位标准差统计图，由图4知观测量使用电离层约束求解宽巷模糊度进行解算，测站点位标准差范围为0.102 0～1.071 0 m；观测量使用基于伪距解算宽巷模糊度进行解算，测站点位标准差范围为0.137 1～1.251 1 m。通过对比发现，观测量使用电离层约束求解宽巷模糊度解算精度较好。因此在非核心区进行北斗二号系统数据处理时，建议使用电离层约束求解宽巷模糊度进行解算。

图4 不同观测量选择测站点位标准差统计

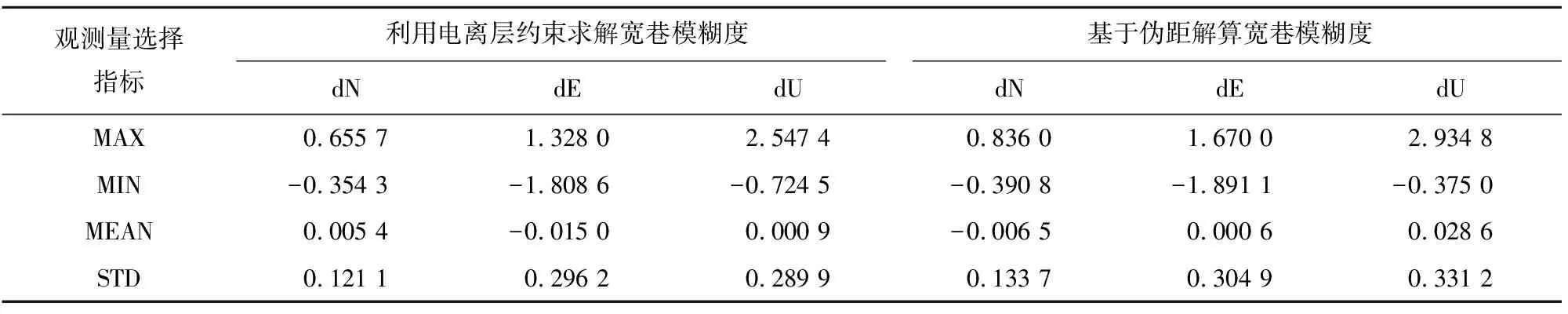
表4 采用不同观测量的解算精度统计

2.4 不同卫星高度截止角对北斗二号系统在非核心区域数据处理精度的影响

GNSS测量过程会受到多路径效应的影响，合理处理多路径效应误差的影响是提高定位精度的关键。采取合适的卫星高度截止角能有效消减多路径效应的影响[16]。

表5为方案4对不同卫星高度截止角作为解算策略进行解算的精度统计，图5为以卫星高度截止角为单位绘制的点位误差统计图。由于对不同截止角连续解算7天，因此将数据解算结果以卫星高度截止角为单位进行标准差统计,通过统计发现卫星高度截止角在0°、5°、10°时精度几乎相同，在12°达到最优，在25°以后有些测站由于卫星高度截止角太高，可用卫星数太少导致解算失败，在40°以后基本没有解算结果。通过统计连续7天解算结果，有1天在11°达到最优，4天在12°达到最优，2天在13°达到最优，因此在非核心区进行北斗二号系统数据处理时建议将卫星高度角设置为12°。

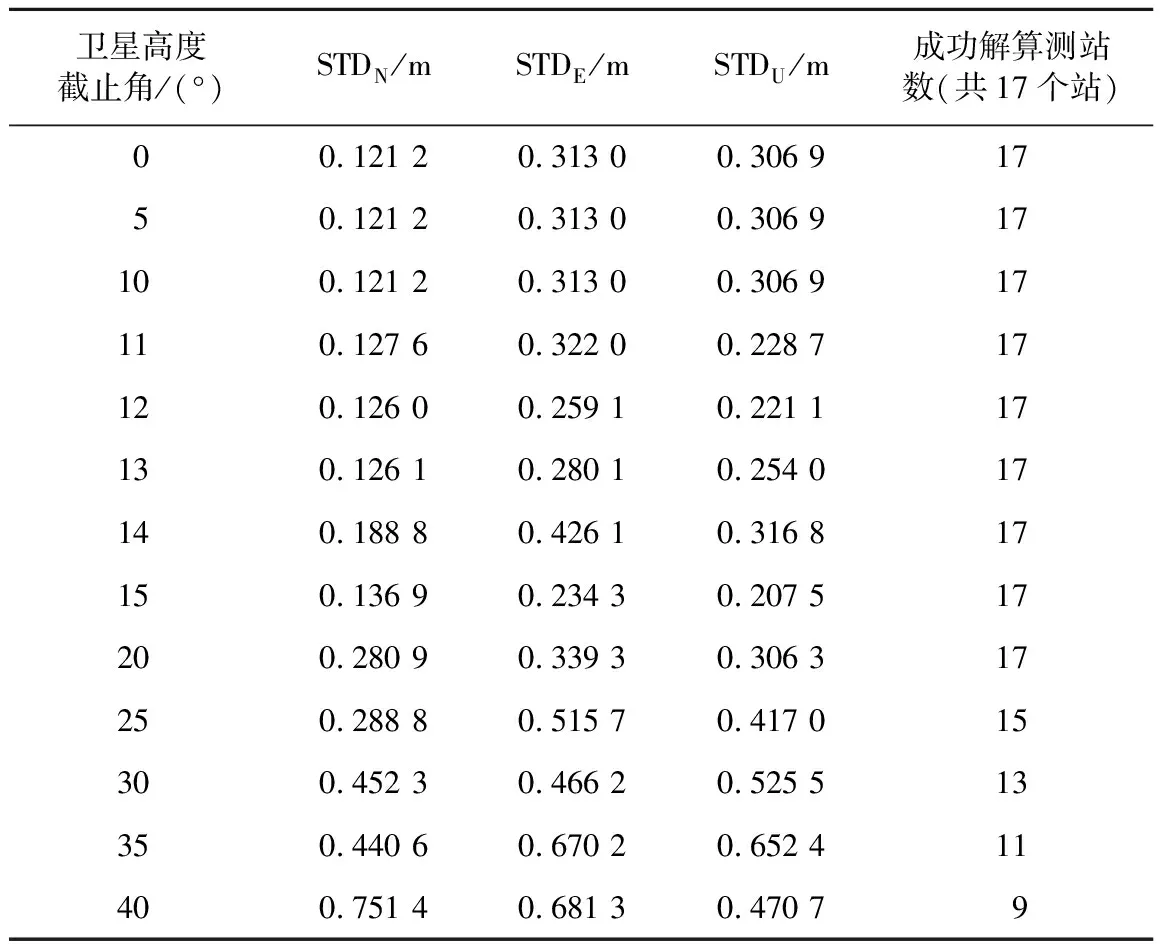
表5 不同卫星高度截止角解算精度统计

图5 不同卫星高度截止角点位标准差统计

2.5 对流层天顶延迟估计间隔对北斗二号系统在非核心区域数据处理精度的影响

GPS信号经过对流层时，传播路径和传播方向均发生变化，从而改变信号到达接收机的传播时间。对流层属于非弥散介质，对信号产生的延迟无法通过相位组合的方式消除。通过对对流层天顶延迟估计间隔时间的设置会影响不同长度的基线解算[17]。

表6为对流层天顶延迟估计时间间隔分别设置为每1、2、4 h各解算一次进行精度统计。结果表明，测站单天GPS解算值与北斗解算值的差值中，最大值达到米级，平均值为厘米级，标准差为分米级。对三组实验分别以测站为单位绘制点位误差统计图，由图6知，最优结果(点位误差最小)中的47.1%对流层天顶延迟估计时间间隔为1 h；最优解算结果中的29.4%对流层天顶延迟估计时间间隔为2 h；最优解算结果中的23.5%对流层天顶延迟估计时间间隔为4 h。通过比较发现，对流层天顶延迟估计间隔设置对于北斗二号卫星系统解算精度影响不明显，对流层天顶延迟估计时间间隔设置为1 h时统计结果较好，但会增加解算时间，因此对精度要求不高或解算测站过多时，可以使用2 h作为解算策略。

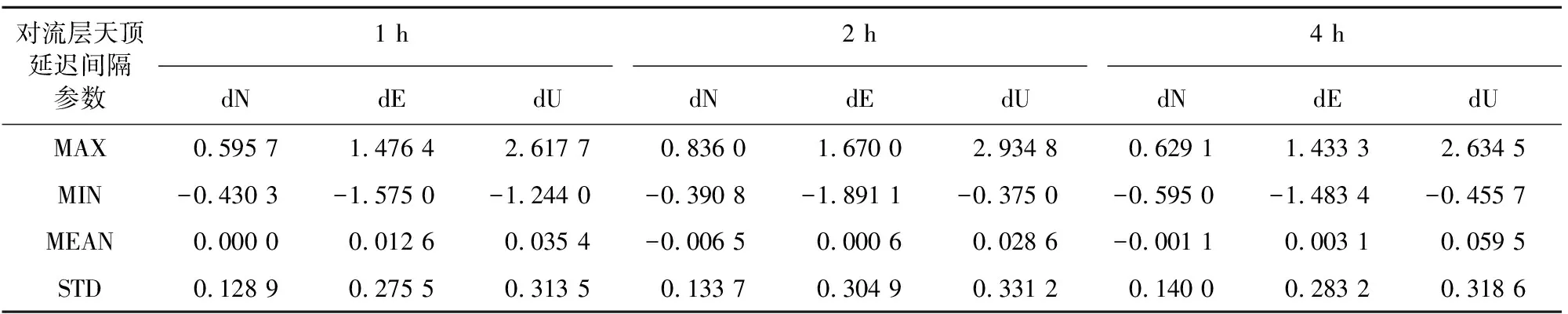
表6 不同对流层天顶延迟间隔解算精度统计

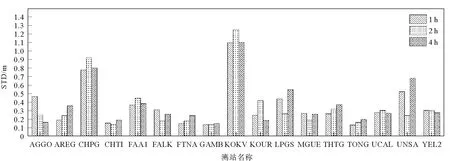
图6 不同对流层天顶延迟估计时间间隔点位标准差统计

3 讨论

卫星轨道精度是影响基线解算结果的重要因素之一，因此在进行高精度GNSS数据处理时，需要使用事后精密星历进行解算。方案1分别使用CODE、WUM、GFZ三个分析中心提供的的北斗二号精密星历进行基线解算，发现三个分析中心处理得到的精密星历不同，采用CODE分析中心提供的精密星历进行北斗二号系统数据解算的精度和可靠性较好。

基线解算策略是影响基线解算精度的又一重要因素。方案2对基线解算策略中的映射函数进行实验，NMF、VMF1、GMF映射函数都以对流层延迟变化为基础，利用全球探空资料、折射资料和相关的气象物理模型等构建，映射函数是影响由对流层模型得到的天顶延迟向传播路径延迟方向转化精度的重要因素，实验发现采用NMF函数解算的相对定位精度较高；方案3对观测量选择进行实验，由于两种观测量均为基于无电离层组合载波相位观测值，不同点在于如何分解LC整周模糊度，通过实验发现电离层约束求解宽巷模糊度的相对定位精度高于基于伪距解算宽巷模糊度；方案4对于不同卫星高度截止角进行实验，适当增大卫星高度截止角能有效消减多路径效应的影响，但太大的卫星高度截止角会减少可观测到的卫星数量，也会影响定位精度，因此通过方案4的研究发现卫星高度角设置为12°能达到较好的解算精度；方案5对于对流层天顶延迟估计时间间隔进行研究，卫星信号经过对流层时，传播路径和传播方向会发生变化。将对流层天顶延迟估计时间间隔分别设置为1、2、4 h进行研究，对流层天顶延迟估计时间间隔设置为1 h时精度较好，与设置为2 h时精度相差不大，但会增加数据处理时间，因此在精度要求不高或解算测站过多时，可以使用2 h作为解算策略。

通过对方案1至方案5的研究，北斗二号系统相对定位精度最大值达到米级，平均值为厘米级，标准差为分米级，目前在北斗二号系统非核心区域内GPS系统定位精度较北斗二号系统高。北斗二号系统作为区域性定位系统，卫星星历星座主要分布于亚太地区，处于非核心区域星历星座分布较少；GPS系统为全球性定位系统，卫星星历星座分布比较均匀。因此测站精度与测站可观测到的卫星数密切相关。

为探究北斗二号卫星系统非核心区域定位精度与测站可观测卫星数的关系。通过对方案1至方案5研究发现，FTNA TONG定位精度较高；CHPG、KOKV定位精度较差。因此将方案2中使用GMF映射函数解算结果中的FTNA、TONG、CHPG和KOKV 4个测站进行精度统计，结果如表7所示。同时对4个测站在观测时段内(2018年年积日020至026)观测到的北斗和GPS卫星数目进行统计，统计结果如图7所示。图7中，横向条带为4个测站在观测时段的卫星数目统计，C为观测到的北斗卫星数，G为观测到的GPS卫星数，右侧条带为观测到的卫星数目标尺，颜色越深表示观测到的卫星数目越多。统计发现测站可观测到的GPS卫星数远远大于北斗卫星数，FTNA和TONG可观测到的北斗二号卫星数目多于CHPG和KOKV，且FTNA、TONG定位精度优于CHPG、KOKV，因此测站观测到的卫星数会影响定位精度。北斗二号系统星历星座主要分布于亚太地区，处于非核心区域星历星座较少，因此在非核心区域制约北斗二号系统定位精度的一个重要因素是测站可观测到的卫星数目过少，从而降低了北斗二号系统在非核心区域的定位精度。

表7 TONG、KOKV、FTNA、CHPG测站信息

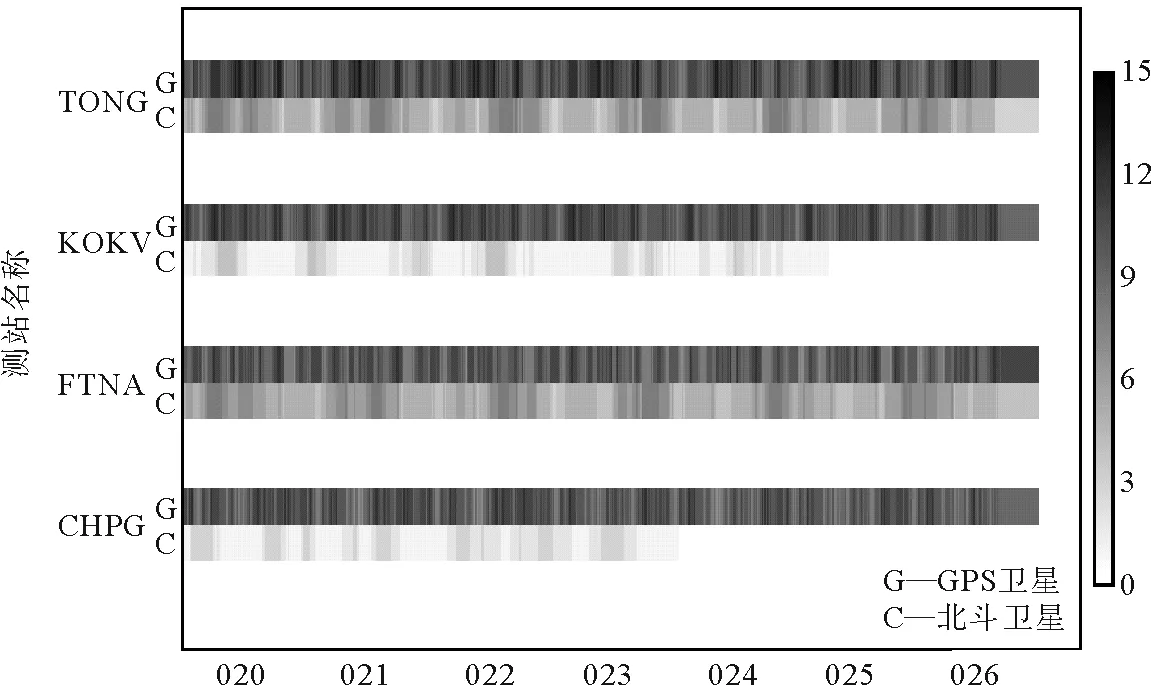
图7 TONG、KOKV、FTNA、CHPG测站观测时段内北斗卫星和GPS卫星数目统计

4 总结

通过对北斗二号系统非核心区域的17个IGS站数据进行解算，分别研究了精密星历和基线解算策略中的观测量选择、卫星高度截止角、干湿映射函数、对流层天顶延迟估计时间间隔对北斗二号非核心区域定位精度的影响，实验结果表明：

1)由于北斗二号系统布网形式及其服务范围主要在亚太地区，因此制约非核心区域定位精度的主要因素是测站可观测到的卫星数目过少。

2)北斗二号系统非核心区域定位精度最大值达到米级，平均值为厘米级，标准差精度达到分米级。

3)在非核心区域对北斗二号系统进行高精度数据解算时，建议使用CODE提供的精密星历，干湿映射函数使用NMF函数，观测量使用电离层约束求解宽巷模糊度，卫星高度截止角使用12°，对流层天顶延迟时间间隔设置为1 h。