近水面爆炸气泡—自由面动态耦合演化特征研究

2021-02-23那立民李炳南姚熊亮王志凯

兵器装备工程学报 2021年1期

那立民，古滨，孙波，李炳南，姚熊亮，王志凯

(1.中国人民解放军91439部队，辽宁大连 116041;2.西华大学土木建筑与环境学院，成都 610039; 3.哈尔滨工程大学船舶工程学院，哈尔滨 150001)

浅水爆炸时，爆炸产生的气泡会与自由面发生强烈的耦合作用，气泡在浮力和自由面的共同作用下，会形成指向或背离自由面方向的射流，形成复杂的水冢现象[1]。这种复杂物理现象在舰船抗爆与防护、水中兵器等国防领域得到了深切关注，对开展水下爆炸水幕反导、舰船抗冲击试验、武器系统设计、毁伤效能分析[2-4]等方面研究都具有指导意义和应用价值[5]。

目前针对浅水爆炸现象的模拟有多种数值方法，Blake等[6]利用边界元方法模拟了气泡距自由面一倍气泡最大半径时气泡的产生、发展和溃灭过程。Wang等[7]采用势流理论对气泡所在的流场进行假设，模拟了超近自由面条件下(半个气泡最大半径的距离)，自由面与气泡的耦合作用。鲁传敬[8]利用轴对称方法分别对两个空化气泡在自由表面附近的动力学特性进行了研究。Pearson等[9]在鲁传敬的基础上，模拟了自由面与单个气泡及两个气泡的相互作用。E.Klaseboer等[10]假设不同流体两侧为不可压缩势流，在交界面上法向速度与压力相等，进行了自由场水下爆炸气泡模拟。张阿漫等人[11]基于边界积分法建立了水下爆炸气泡与自由面耦合数值模型，讨论了基于Kelvin-impulse理论Blake准则的适用范围，并解释了Blake准则的失效原因。李帅等[12]采用边界元法对皇冠水冢出现珠化现象之前的过程进行模拟。Li等[13]利用Dytran软件，开展了近自由面水下爆炸气泡运动形态研究，并得到了较高的仿真精度。致斌伟等[14]通过对比Dytran和PAM-FLOW软件计算结果，发现了较为一致的结果现象。张阿漫等[15]利用电火花实验，发现了浅水条件下，近自由面水下爆炸会产生多种水冢形态，分别为破碎型、溅射型、皇冠型、冲天型、丘型和微鼓型。李梅等[5]进行了1 kg球形RDX装药在不同起爆深度下的海上爆炸实验，通过高速摄像机记录装药起爆后水柱的形成和成长过程，获得了喷射水柱形态的演变特征以及水柱高度、直径、水柱突出水面时间等参数的变化规律。崔杰[16]通过采用减压条件下的电火花试验方法，总结了不同浮力参数、距离参数下产生的水冢形态差异与诱因。唐廷[17]等通过综合近年来舰船结构对水下近距爆炸响应的研究成果，阐明了水下近距爆炸载荷的理论、实验和数值研究进展，并分类总结了水下近距爆炸时的流体结构相互作用与平板、圆柱壳、梁和舰船结构响应的研究现状。

目前，有关水下爆炸诱导水冢形态的公开文献发表成果主要集中在皇冠型和酒杯型，而对其他几种水冢形态研究较少，即使是在数值方面。一方面是水下爆炸气泡与自由液面的距离太近，气泡膨胀过程中会发生漏气和破碎现象，该现象的数值模拟比较困难；另一方面这些特殊的物理现象都是在气泡射流之后较长时间内发生的，而目前的数值模型多是集中在模拟环状气泡撕裂之前，而且气泡射流完成到涡环撕裂所用时间很短，水冢形态基本还处于简单的山峰形态。

本文借助LS-DYNA中ALE算法，充分利用Lagrange方法和Euler方法的优势，构建数值仿真模型，通过合理设置边界条件、网格参数等，保证模型具有较高的计算稳定性和多相流复杂界面的处理能力，进行爆炸气泡—自由面动态耦合计算。并以此为基础，研究了60 kg TNT距水面不同爆距比条件下，气泡与自由面的动态耦合演化情况，有助于提高对水冢形态、成长过程和形成机理的深入认识。

1 数值算法验证

1.1 ALE方法

本文采用LS-DYNA软件中自带的ALE算法，为方便指导开展自由面水冢与浮体间的相互作用研究，故对ALE算法进行简单介绍。ALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。这种方法兼具Lagrange方法和Euler方法二者的特长，在结构运动处理上结合了Larange方法，能够有效的跟踪物质结构边界运动；在内部网格的划分上，又融合了Euler法的优点，使内部网格单元独立于物质实体而存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，如图1所示，使得网格不致出现严重的畸变。这种方法在分析大变形问题时是非常有利的。

图1 任意的拉格朗日欧拉耦合网格移动示意图

ALE法共运用了3种坐标系，其中空间坐标系和物质坐标系是所熟悉的常规坐标系，网格坐标系才是ALE法最核心的思想所在，它将另外两个坐标系有机结合在了一起，网格坐标系可以如拉格朗日法在界面追踪物质的运动，也可以如欧拉法在内部与空间坐标重合，甚至可以做到在一方向运动而另一方向固定，因此可以求解像爆炸这种引起大变形的网格计算，并可以降低网格的扭曲程度。

在ALE法中，选某一参考体，记初始时刻t0和发生形变t时刻后的参考体分别为Δx和Δχ，引入另外的一个参考构型，用Δk代替。引入新的参考坐标系OK1K2K3，并使用该坐标系来描述Δk中相应参考点的位置坐标。从而，ALE算法下任意函数g的随体倒数表示为：

(1)

其中，对流速度为cα=uα-ωα，uα为质点X的物质速度；ωα为参考点κ的物质速度，即网格速度。这样，在ALE算法下所描述的控制方程主要有：

1) 质量守恒控制方程：

(2)

2) 动量守恒控制方程：

(3)

3) 能量守恒控制方程：

(4)

其中，ρ为密度；fα为单位质量的张力；σαβ为柯西应力张量；e为单位质量的内能；qα为热通量。

1.2 ALE算法常用欧拉体材料参数

在LS-DYNA软件中，把不同物体分成不同的PART建模，并给这些part赋予不同的材料，对于体材料我们还需要赋予状态方程，在水下爆炸计算中，常用的欧拉体材料有空气、水、炸药等，三者之间在空气中是相互独立的，在爆炸计算时，又会进行相互作用。主要是能量的相互渗透、力的相互作用、网格的相互穿插等。

1) 空气

空气与水界面交界处是发生反应的关键地方，当气泡半径大于炸药到自由液面的距离时，在该关键位置就会出现水冢现象，因此，空气介质在水下爆炸中也起着重要影响。空气的状态方程一般采用LINEAR-POLYNOMIAL MODEL方程表示，描述如下：

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(5)

(6)

式中：C0、C2、C3、C4、C5、C6为试验测得的常数；E为单位体积的能量。

根据γ定律空气系数：

C0=C1=C2=C3=C6=0

(7)

C4=C5=γ-1

(8)

将上述式(7)、(8)代入式(6)可得到新的状态方程形式：

(9)

该方程就是简化后需要的空气状态方程，其相关参数见表1。

表1 空气介质的相关参数

2) 水

水采用*MAT_NALL 材料模型，采用Gruneusen状态方程，即

(10)

表2 水的状态方程参数

3) 爆轰产物

用于描述炸药爆炸状态的方程形式有很多，其中应用较多的有γ律方程、LDJ、JWL等，本章中使用的炸药为TNT炸药，所用到的状态方程为JWL方程，表现形式为：

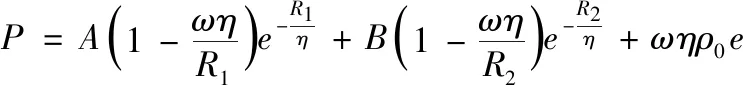
(11)

式中：r1为爆炸产物与初始炸药两者之间密度的比值，即η=ρ/ρ0；A、B、R1、R2、ω为炸药有关的参数，见表3；e为TNT炸药单位质量的内能。

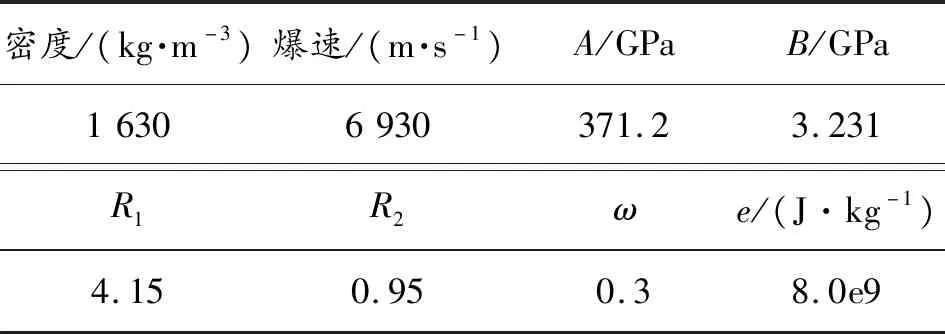
表3 TNT炸药状态方程参数

1.3 有限元模型

首先引入近水面水下爆炸气泡脉动的实验研究[13]，以验证有限元模型建立、边界条件以及算法的适用性。实验描述如下：4 g PETN混合炸药(成分为70%PETN，20%铝，10%遏制物质，可等效为5.2 g TNT炸药)在2 m长的钢制正方体水箱中进行自由场水下爆炸实验，爆心位于水下0.13 m。本文中有限元模型完全与实验模型相同，边界条件选择为4周及底面为刚性壁面边界条件，上方给与大气压力加载，重力场则是通过不同水深处的静水压力不同模拟出来的。具体工况示意图如图2。

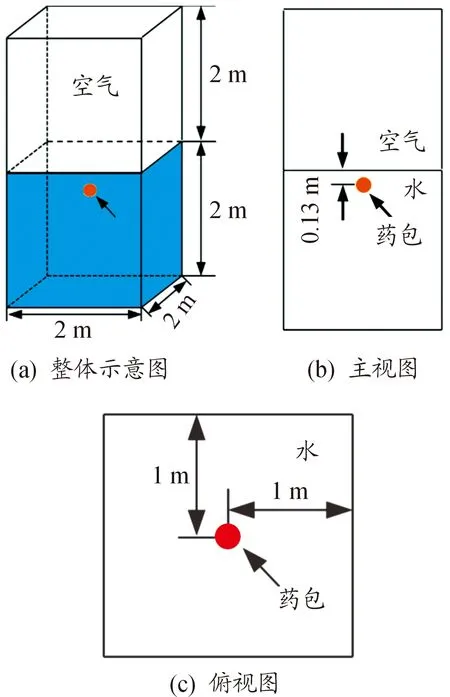
图2 4 g PETN炸药水下0.13 m处爆炸气泡工况示意图

由于在不同的工况，结构和流场的物理特性存在较大差异，使其具有较大的局限性。所以采用无量纲参数λ=d/r，其中，d为网格尺寸，r为药包半径，对水下爆炸气泡脉动网格尺寸效应进行初步探索。4 g PETN混合炸药在2 m×2 m×2 m的钢制正方体水箱中进行自由场水下爆炸实验，TNT采用球形装药(由炸药质量和密度可以求出药包半径)，r为药包半径为9.132 mm，在药包爆点附近各个方向0.5 m处为均匀网格，为了减小计算量，距药包爆点0.46 m(2倍气泡最大半径)以外处采用渐变网格(对气泡半径影响较小可忽略不计)，对于均匀网格，尺寸大小分别为λ=0.9(网格尺寸为8.219 mm)，λ=1(网格尺寸为9.132 mm)，λ=1.1(网格尺寸为10.045 mm)，λ=1.2(网格尺寸为10.958 mm)λ=1.3(网格尺寸为11.872 m)λ=1.4(网格尺寸为12.785 mm)渐变网格从里至外逐渐增大，在最外侧网格大小为0.1 m。

1.4 计算结果与实验结果对比

图3为4 g PETN炸药在水下0.13 m处文献[16]的实验结果与本文的数值计算结果图，观察气泡形态，当炸药爆炸后，在爆点位置处产生爆炸膨胀气泡，在19.66 ms体积达到最大，然后开始收缩，由于浮力小于自由面引起的Bjerknes力，故气泡被自由面击退，气泡中心位置远离自由面，在26.17 ms开始进行射流，汽水混合物开始从气泡底部流出，同时气泡的其他部分也开始被破坏，直到42.67 ms气泡体积达到最小值，并开始继续下一周期的膨胀。比较实验结果和数值仿真结果，发现数值结果的气泡形态以及产生相应形态所对应的时刻，两者具有高度的一致性，由此可以认为有限元模型的建立、边界条件设置的正确性，同时本次使用的ALE方法能够较好的模拟近水面条件下，爆炸气泡的膨胀、收缩、射流、溃灭等复杂现象，可以进行下一步更深层次的工作。

图3 4 g PETN炸药水下0.13 m处爆炸气泡实验结果与数值计算结果

2 近水面水下爆炸气泡强耦合运动特性研究

2.1 工况设置

E.Klaseboer[18]首先基于一定的假设总结出TNT炸药爆炸时，气泡最大半径的经验公式如式(12)所示，

(12)

式中：W为装药当量(kg);h为爆炸深度(m)。

因为本文主要是为了实际工程应用进行计算，选择比较大当量的60 kg TNT炸药为背景依据。查阅文献[15]，水冢形成主要与炸药质量和炸药距水面距离有关，故本文引入竖直无量纲距离参数γ=h/Rmax，h为气泡中心距离水面距离，Rmax为气泡最大半径。控制炸药质量不变，改变气泡距水面距离，代入(12)，计算出气泡最大半径，得到不同距离参数工况，约70余组，讨论距离参数对水冢的影响[18]。

2.2 水冢形态及演变特征分析

2.2.1 零碎型水冢

图4所示为零碎型水冢，此时自由液面距离气泡中心0.23 m，气泡最大半径为6.03 m左右，无量纲距离为γf=0.04。当在t=0.005 s时，气泡开始出现，但由于距离自由面过近，气泡内气体与自由面以上气体相通，在自由面与气泡接触处，形成少量四处飞溅的水幕，同时气泡大部分出现在空气中，由于静水压力的影响，气泡上粗下扁。此时气泡内压大于外压，气泡开始迅速膨胀，呈现出两头尖、中间扁的形状，并且空气中的气泡体积大于水中的气泡体积。在t=0.055 s时，气泡体积膨胀到最大值，开始收缩，并开始碎裂。t=0.195 s时可以看到气泡在空气中的部分已经碎裂成很多部分，大部分向上飞去，在水中的气泡重新组合成一个小的气泡，继续开始收缩运动，水面有水柱上升。为了便于在后续过程中，观察水面上的水冢现象，在以后的后处理中，将空气中影响观察的杂乱气体移除。t=0.395 s时下方气泡收缩到最小值，此时自由面形成细长水柱。t=0.555 s时气泡开始向下射流，射流速度为38 m/s。在t=1.035 s时，发现气泡已经碎裂成许多部分，小气泡由于浮力较小开始向下运动，大部分气泡由于Bjerknes力效应减弱，气泡受浮力作用效果更大，气泡中心位置开始持续上浮，此时自由面上方形成零碎型水冢。在t=1.615 s时，此时气泡底部上升到原自由面上方，下一时刻气泡开始碎裂，整个飞溅型水冢不再受气泡作用力，由于具有初速度，水冢碎裂更加严重。直到速度为0，最后由于重力，按竖直向下的速度开始做自由落体运动，直到整个水冢完全融入水中。

2.2.2 飞溅型水冢

图5所示为飞溅型水冢，自由液面距离气泡中心为0.5 m，气泡最大半径为5.98 m左右，此时无量纲距离γf=0.08，此时没有形成完整的气泡周期和气泡射流。t=0.005 s、t=0.06 s、t=0.12 s自由面与气泡变化形式与γf=0.04完全一致。气泡在t=0.06 s时膨胀到最大体积，并开始收缩，气泡发生碎裂。在收缩过程中，空气开始进入到水中原来气泡位置，并与原来的部分气泡一起形成一个新的与自由面联通的气泡，在t=0.12 s时，气泡体积收缩到最小，并开始膨胀，自由液面受其推动，形成向上方中间聚拢运动的水幕。为了便于观察水冢形态，在后续后处理时，将气泡移除不显示。在t=0.22 s时，气泡体积膨胀到最大值，开始收缩，自由液面上方形成圆锥形水幕，因为原有速度，并向中间上方聚拢。在t=0.46 s时，水幕在中心处合成一条水柱，并与气泡外部携带的水合在一起，水域中气泡封闭，与空气不在联通，闭合气泡继续收缩，水柱继续向上运动。在t=0.71 s时，气泡收缩到最小值，向上方移动，并发生射流，射流速度为4 m/s，形成t=0.91 s时刻的飞溅型水冢，此时新形成气泡破碎，与空气域联通，整个飞溅型水冢不再受气泡作用力，由于具有初速度，继续上升，直到上升到最高位置，最后按竖直向下的速度开始做自由落体运动，直到整个水冢完全融入水中。

图4 γf=0.04时爆炸气泡及自由面水冢演变过程示意图

图5 γf=0.08时爆炸气泡及自由面水冢演变过程示意图

2.2.3 酒杯型水冢

图6所示为酒杯型水冢，此时自由液面距离气泡中心3.23 m，气泡最大半径为5.55 m左右，无量纲距离γf=0.58，从上图可以看出，此时气泡具有完整的周期结构和明显的射流，在t=0.315 s时气泡体积达到最大值并开始收缩，自由面已经形成明显水冢，在t=0.575 s时刻气泡开始射流，射流速度为59.2 m/s。t=0.675 s时刻自由液面水柱高度继续增加，气泡坍塌到最小体积，并开始碎裂，每个碎裂的气泡并开始膨胀，此时自由面的Bjerknes力效应减弱，浮力对于气泡作用更明显，气泡中心位置开始持续上浮。在t=0.885 s时刻气泡体积膨胀到最大值，体积开始缩小，水冢继续上升，同时由于气泡坍塌后滞后流的强烈作用，在沿着环状气泡载荷的方向，自由液面中心附近的水柱周围形成薄壁台阶状的水冢，同时中心水柱和周围的薄壁水冢继续上升。在t=1.155 s时刻薄壁水冢上方开始脱离，并向四周呈飞溅状，最后形成t=1.345 s时的皇酒杯型水冢。

2.2.4 皇冠型水冢

图7所示为皇冠型水冢，此时自由液面距离气泡中心8.23 m，气泡最大半径为5 m左右，无量纲距离γf=1.65，此时气泡可以形成完整的周期结构和明显的射流。在t=0.006 s、t=0.67 s，对应气泡最大体积、最小体积时刻。t=1.102 s气泡开始向上射流，并推动自由面向上运动，射流速度与自由面运动速度几乎相同，速度为24.2 m/s，射流宽度为2 m，此时气泡开始开始缩小。在t=1.302 s时可以看到，与酒杯型水冢类似，伴随着气泡的第二次膨胀时刻，由于气泡坍塌后滞后流的强烈作用，在沿着环状气泡载荷的方向，自由液面中心附近的水柱周围形成薄壁台阶状的水冢，同时中心水柱和周围的薄壁水冢继续上升，上升初始速度约为12.9 m/s。在t=1.79 s时，气泡开始破碎，以后探讨中将其移除，中心水柱继续上升，周围皇冠围裙继续向上升，形成t=2.35 s 时的皇冠型水冢。

图6 γf=0.58时爆炸气泡及自由面水冢演变过程示意图

图7 γf=1.65时爆炸气泡及自由面水冢演变过程示意图

2.2.5 莲花型水冢

图8所示为莲花型水冢，此时自由液面距离气泡中心12.23 m，最大半径为4.68 m左右，无量纲距离γf=2.61，类似于皇冠型水冢，在t=0.006 s、t=0.966 s时刻，对应气泡最大体积、最小体积时刻，在t=0.966 s时气泡开始出现朝向自由面的射流，在t=1.27 s时刻气泡已经缩小到最小体积，开始继续膨胀，自由面由尖丘型逐渐变成椭圆形，此时在气泡的作用下，自由面出现台阶形状并获得一定的速度向上运动，气泡呈葫芦状，并在最顶方由于速度过大，带动少量水脱落一直向上运动，在t=1.766 s时刻气泡开始破碎，最后形成t=2.214 s时的莲花型水冢。

2.2.6 山丘型水冢

图9所示为山丘型水冢，此时自由液面距离气泡中心14.23 m，最大半径为4.55 m左右，无量纲距离γf=3.13，在t=0.006 s、t=0.966 s时刻，对应气泡最大体积、最小体积时刻，在t=0.966 s时气泡开始射流，类似于莲花型水冢，此时气泡中心距离自由液面太远，自由液面基本不受气泡影响。在t=1.27 s时刻气泡已经缩小到最小体积，并开始继续膨胀，在t=1.766 s时，气泡开始破碎，水冢在滞后流的影响下变窄变高，最后形成t=2.214 s时的山丘水冢。

2.3 水冢形态验证与主要影响因素

图10所示数值结果与实验结果水冢形态，上面为文献[16]的实验结果。下面为本次数值计算结果，通过对比，可以发现本次数值计算水冢形态与实验结果水冢形态具有高度的一致性，说明本次数值计算的有效性。

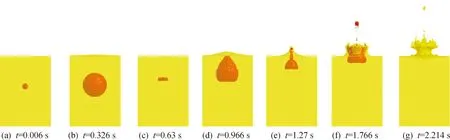
图8 γf=2.61时爆炸气泡及自由面水冢演变过程示意图

图9 γf=3.3时爆炸气泡及自由面水冢演变过程示意图

图10 文献[16]的实验结果与本文数值计算结果水冢形态示意图

由于本文是按照实际工程中工况进行计算，模拟的都是常压条件下的工况，而且每次工况时的浮力参数也几乎相同，所以本文并没有讨论浮力参数的影响，只是探讨无量纲距离参数γf对水冢形态与演变特征的影响。在不同距离参数γf情况下，由于产生的气泡的脉动情况及运动情况不同，导致自由面的变化也不相同。通过大量工况计算，总结出水冢形态与距离参数γf的关系如图11所示。

图11 水冢形态分布随距离参数γf变化示意图

2.4 水冢参数化研究

零碎型水冢和飞溅型水冢的形态不稳定，而酒杯型水冢、皇冠型水冢、莲花型水冢、山丘型水冢形态比较稳定，能够统计水冢形态主要参数。对于莲花型水冢和山丘型水冢由于距离自由面过远，产生现象并不明显，故本次只是统计酒杯型水冢和皇冠型水冢主要参数，参考文献[12]，为了方便分析，将其统一定义参数，将中心水柱定义为皇冠主峰，将水柱中心的台阶状水冢定义为皇冠围裙。李帅等给出的皇冠水冢参数示意图[12]如图12。

图12 李帅等人给出的皇冠水冢参数示意图

1978年，Swisdak[19]进行大量小当量水下爆炸实验，并总结实验数据，得出近水面水下爆炸形成水冢最大高度与药量和距水面爆距之间的关系。并总结出水冢最大高度与药量、爆距关系的经验公式：

(13)

(14)

式中，Hmax为水冢能上升的最大高度(m)；W为炸药质量(m);Y为爆心初始时刻所在深度(m)。对于酒杯型水冢和皇冠型水冢，水冢最大高度远低于Swisdak总结的经验公式计算结果，这主要是因为大当量近距离水下爆炸时，气泡浮力较大，很快就上升到自由面破碎，有许多能量浪费；随着爆距无量纲参数增加，围裙宽度和围裙高度变化不大，这是因为皇冠围裙是由于当气泡坍塌后滞后流和气泡膨胀时的气泡脉动压力的强烈作用，在沿着环状气泡载荷的方向形成产生的，故围裙宽度主要与气泡半径有关，围裙高度主要与气泡载荷有关，而各工况气泡半径和气泡载荷在上升到自由面附近时变化不大。随着爆距无量纲参数增加，皇冠主峰高度先减小后增大，且在距离较近时，高度迅速减小，在爆距比大于1.5时，皇冠主峰高度变化不大。这是因为距离较近时，皇冠主峰上升主要是气泡直接膨胀直接作用到自由面上，使自由面上升，随着距离变远，气泡脉动作用到自由面上的力减小。当爆距比达到1时，由于线性自由面的虚像理论：当气泡更接近自由面时，对浮体的压力和诱导速度势被自由面上方的虚像抵消的越多，气泡载荷对自由面的作用力反而随爆深的增加而增加，当爆距比大于1.5时，此时第二周期脉动力变化不大，皇冠主峰高度变化不大，爆距比再增加就会出现气泡第三周期脉动，形成莲花型水冢和山丘形水冢，不再是皇冠型水冢。