基于刚柔耦合模型的某手枪自动机动力学仿真研究
2021-02-23姚养无李树军
贺 磊,姚养无,李树军,丰 婧
(1.中北大学 机电工程学院,太原 030051; 2.宁波军鸽防务科技有限公司,浙江 宁波 315000;3.中北大学 信息与通信工程学院,太原 030051)
自动武器发射过程时间短,运动和受力复杂,使用UG和ADAMS软件对自动武器进行建模和仿真,可以较为全面地分析研究自动武器发射过程的动态特性[1]。但是,当自动武器中存在柔性件时,如果在ADAMS中仍将柔性件定义为刚体,则其在仿真过程中不会发生弹性变形,这会降低仿真精度甚至导致仿真失败。
1996年,ADAMS推出ADAMS Flex模块,实现了同时包含刚体和柔体的机构动力学分析。ADAMS中的柔性体分为离散式和模态式2种:离散式柔性体是把一个刚体构件离散为几个小刚性构件,小刚体构件之间通过柔性梁连接,离散式柔性体的变形是柔性梁的变形,并不是小刚体构件的变形,这种柔性体可以模拟物体的非线性变形,但只适用于简单结构;模态式柔性体是由ADAMS Flex模块或外部有限元软件生成,能根据构件的实际结构进行复杂建模,这种柔性体采用的是模态叠加法来模拟物体变形,故仅适用于线性结构的受力分析[2]。
本文首先使用三维绘图软件UG绘制某手枪各零部件的三维模型并将绘制好的三维模型按其位置关系装配,将装配好的三维模型以Parasolid格式导入多体系统动力学分析软件ADAMS中,在ADAMS中根据某手枪的受力关系施加载荷和约束,设置仿真参数,利用有限元分析软件ANSYS导出的.mnf文件替换模型中的压杆,利用ADAMS生成的离散式柔性体替换模型中的扳机簧,得到某手枪的刚柔耦合模型。通过对该刚柔耦合模型进行仿真分析,得到某手枪套筒、身管的运动特性曲线以及弹壳在抛壳过程中的运动轨迹,并分析了模态式柔性件压杆和离散式柔性件扳机簧的受力变形情况,为该手枪的进一步优化提供了依据。
1 某手枪发射过程分析
某手枪是一种半自动手枪,采用枪管短后坐自动方式、枪管偏移式闭锁机构、击锤式击发机构,有手动保险、握把保险和空仓挂机装置。击发后,火药气体通过推动套筒和枪管共同后坐一段距离(自由行程),枪管受到铰链限制停止运动,而套筒继续后坐并完成抽壳、抛壳、压倒击锤、压缩复进簧等动作;复进时,靠复进簧伸张推动套筒复进并完成推弹入膛,套筒撞击枪管尾端带动枪管一起复进完成闭锁。其结构原理简图如图1。

图1 某手枪自动机结构原理示意图
2 某手枪刚柔耦合虚拟样机的建立
为了便于仿真,在不影响模型合理性的前提下作以下基本假设:
1) 除压杆、扳机簧、弹簧外,其他运动构件均为刚体;
2) 不考虑子弹发射时作用在身管上的阻力,火药气体直接作用于套筒弹底窝中心;
3) 弹簧阻尼忽略不计。
某手枪由套筒、身管、套筒座、击发机构、弹匣等组成。根据各零件的尺寸参数,利用三维绘图软件UG绘制该手枪的三维实体模型,隐藏不涉及本文研究内容的零部件后,将装配好的模型导出为Parasolid格式(.x_t文件),然后将其导入多体系统动力学仿真软件ADAMS中。
在ADAMS界面中生成一段离散式柔性体以替代原模型中的扳机簧。在ANSYS Workbench界面中为压杆划分网格,以.dat文件形式导入ANSYS APDL界面中并为其定义外接点,然后输出.mnf文件。在ADAMS界面里导入.mnf文件使压杆柔性化以替代原模型的刚性压杆。建立好的虚拟样机模型如图2所示。

图2 某手枪刚柔耦合虚拟样机模型
根据某手枪的实际发射情况,考虑的载荷参数主要有扳机力、膛底合力、碰撞力、弹簧力和抽壳阻力:
1) 扳机力
单动手枪的扳机力一般为15~35 N[3],选取30 N作为虚拟样机模型中扳机力的大小。
2) 膛底合力
作用于膛底的火药燃气压力是某手枪自动机产生运动的原动力。运用经典内弹道计算模型在MATLAB中生成的平均压力随时间变化的计算曲线如图3虚线所示,试验测得的内弹道试验曲线如图3实线所示,计算曲线与试验曲线的拟合度较好,故可以作为某手枪发射时的膛内平均压力曲线。在MATLAB中将平均压力曲线上点的横纵坐标提取出来导入ADAMS中生成样条曲线,用AKISPL函数以力的形式加载到套筒弹底窝中心。通过经验公式将平均压力转化为膛底压力,从而求得膛底合力,相关公式为
(1)
Fgh=SpT
(2)
式中:φ1为次要功计算系数;ω为装药量;m为弹丸质量;Fgh为膛底合力;S为枪膛横截面积。
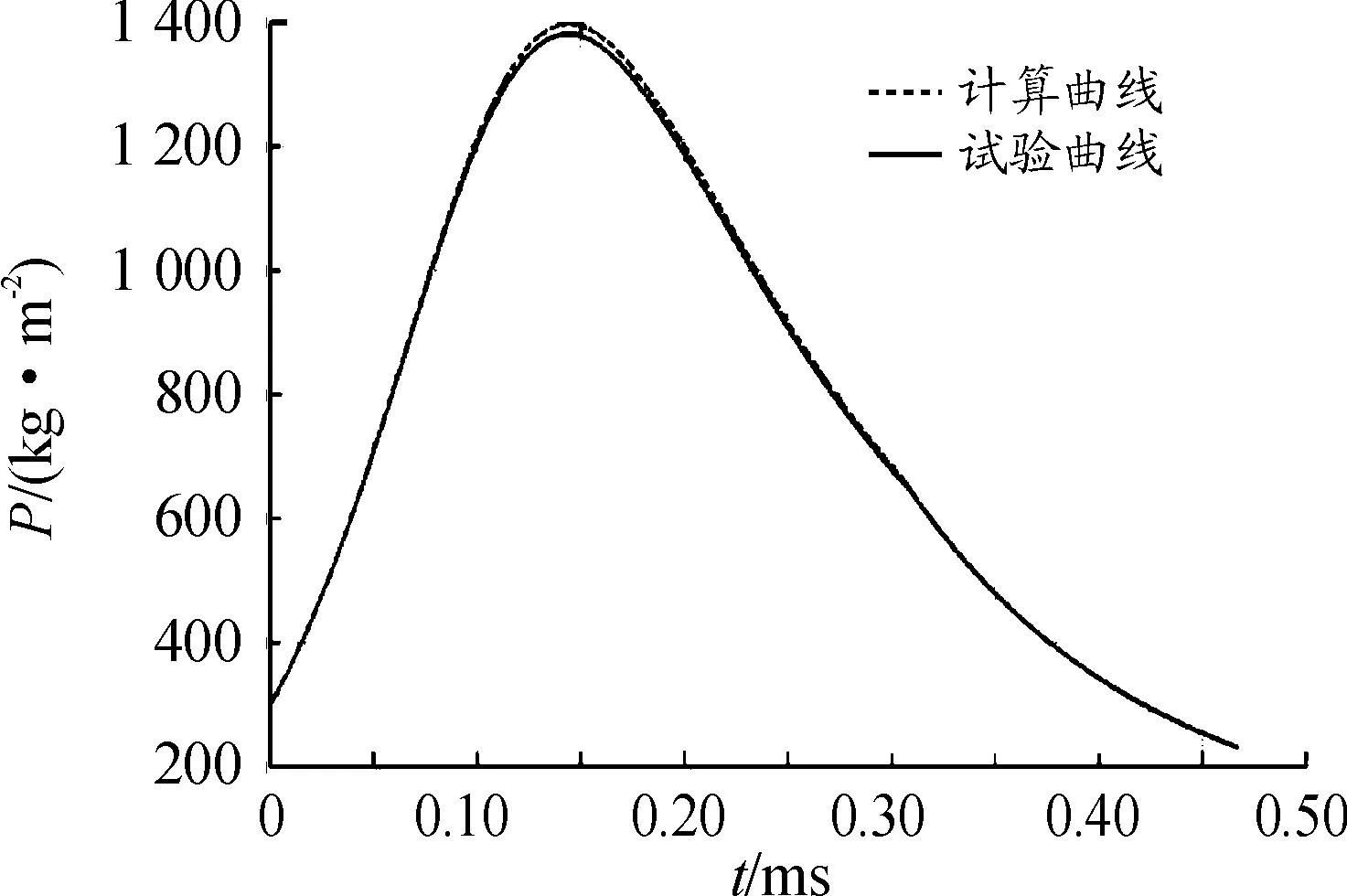
图3 某手枪内弹道曲线
3) 碰撞力
运用ADAMS提供的Impact给模型施加碰撞力,其力学模型为
(3)
式中:k为刚度;δ为穿透深度;C为阻尼;n为力指数。
4) 弹簧力
该手枪中的弹簧有复进簧、击针簧和击锤压杆簧,参数如表1所示。
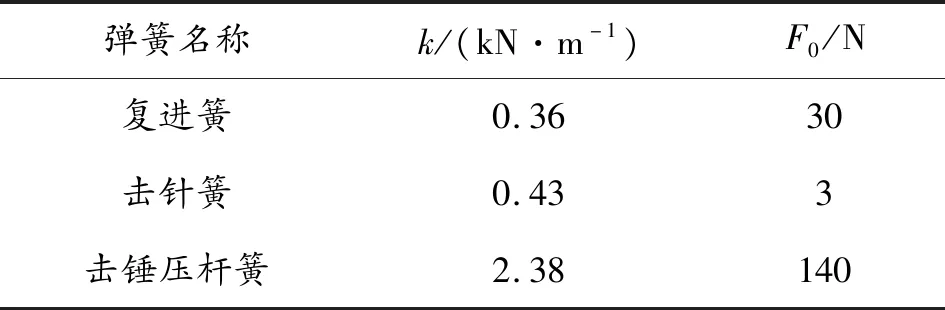
表1 弹簧参数
5) 抽壳阻力
抽壳阻力Fφ是指拉壳钩从身管中把弹壳拉出来时所遇到的阻力,可由拉壳阻力的近似公式得到:
(4)
式中:f0为弹壳与弹膛之间的摩擦因数;lk为弹壳在弹膛内的总长;d1为弹壳内径;E1为弹壳材料的弹性模量;δ为弹壳壁厚;Δ为弹壳外表面与弹膛壁间的相对紧缩量;dpj为弹壳的平均直径;α为弹壳锥型部的半锥度角;x为弹壳后退行程。
在添加完载荷之后,还要在各部件之间添加约束,各活动部件的约束关系如表2所示。
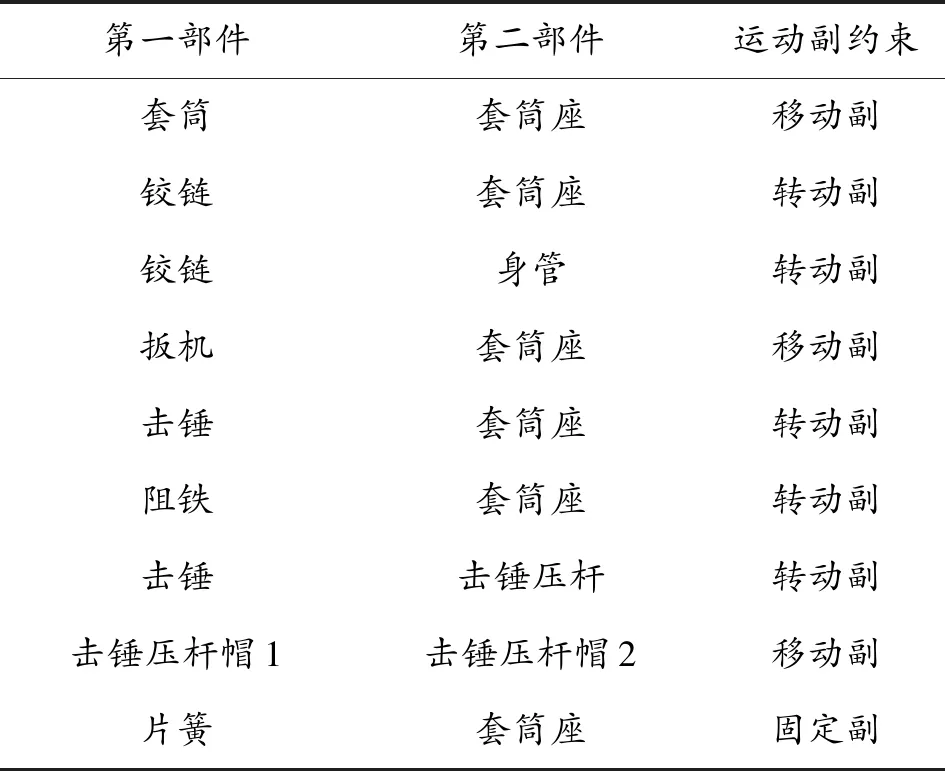
表2 活动部件之间的运动副约束
为了验证刚柔耦合模型的可信度,将虚拟样机的仿真结果与试验结果进行了对比。选取射击时套筒到达各关键位置的时间作为刚柔耦合模型的校核标准,仿真结果与试验结果进行对比,如表3所示。
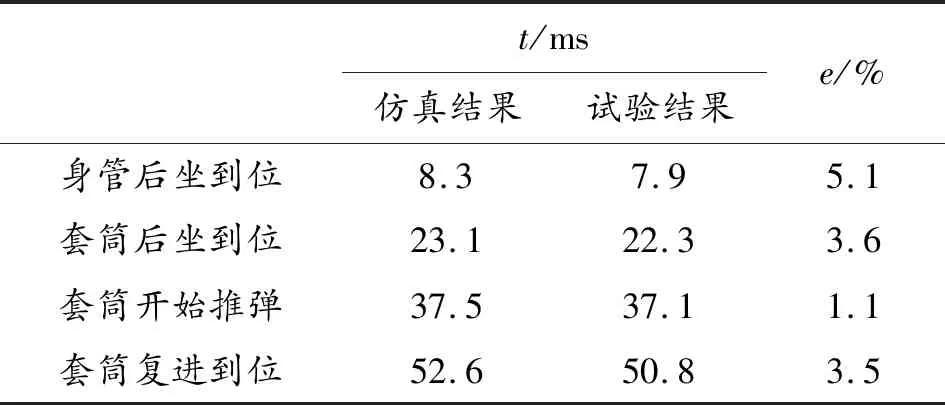
表3 仿真结果与试验结果对照
3 某手枪柔性件动力学特性分析
3.1 柔性压杆动力学分析
柔性压杆首先受到扳机横向力作用,受力变形后推动阻铁释放击锤;在后坐过程中柔性压杆受套筒内弧形槽作用向下运动,在运动过程中受到柔性片簧的支撑;在套筒复进到位后,柔性压杆再次被套筒施压,最后停留在套筒弧形槽内。图4为柔性压杆在Ansys Workbench中的网格模型,表4为柔性压杆在刚柔耦合模型仿真过程中的热点表。

图4 柔性压杆网格模型示意图
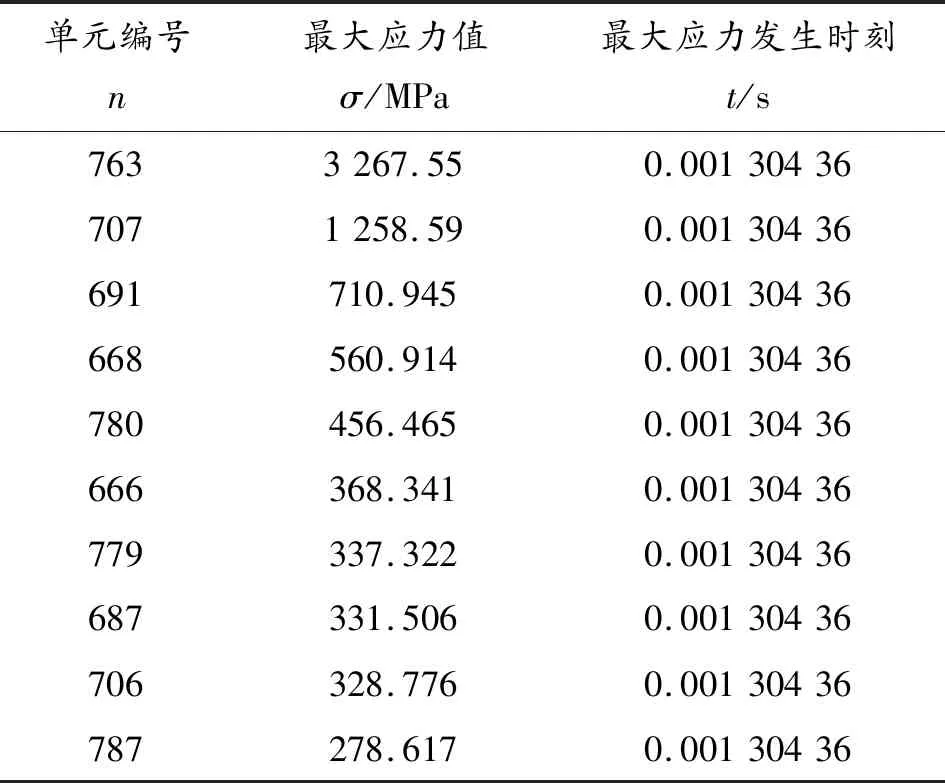
表4 柔性压杆仿真过程热点数据
如表4所示,柔性压杆在0.001 3 s时受力最大,其中,第763号单元受到的等效应力最大,为3 267.55 MPa。
3.2 柔性扳机簧动力学分析
柔性扳机簧被分为100个小矩形刚体,之间由柔性梁连接。在后坐过程中,柔性扳机簧在柔性压杆的推动下发生弯曲并支撑着柔性压杆,在套筒复进到位后推动扳机复位。图5为柔性扳机簧在ADAMS中的简化模型,图6为柔性扳机簧在刚柔耦合模型仿真过程中的变形曲线。

图5 离散式柔性扳机簧简化模型示意图
由图6所示,100号单元由于被固定,所以其在X轴的位移为0,1号单元在仿真过程中处于稳定状态时其X轴坐标为-53.10 mm,其在套筒复进到位后X轴的坐标为-49.98 mm,故柔性扳机簧在在X轴方向的最大位移为3.12 mm。

图6 离散式柔性扳机簧变形曲线
4 某手枪发射动力学特性分析
对某手枪刚柔耦合模型进行动力学仿真计算,得到其发射动力学特性。图7为身管速度、位移曲线,图8为套筒速度、位移曲线,图9为弹壳在抽、抛壳过程中的运动路径。

图7 身管位移、速度曲线
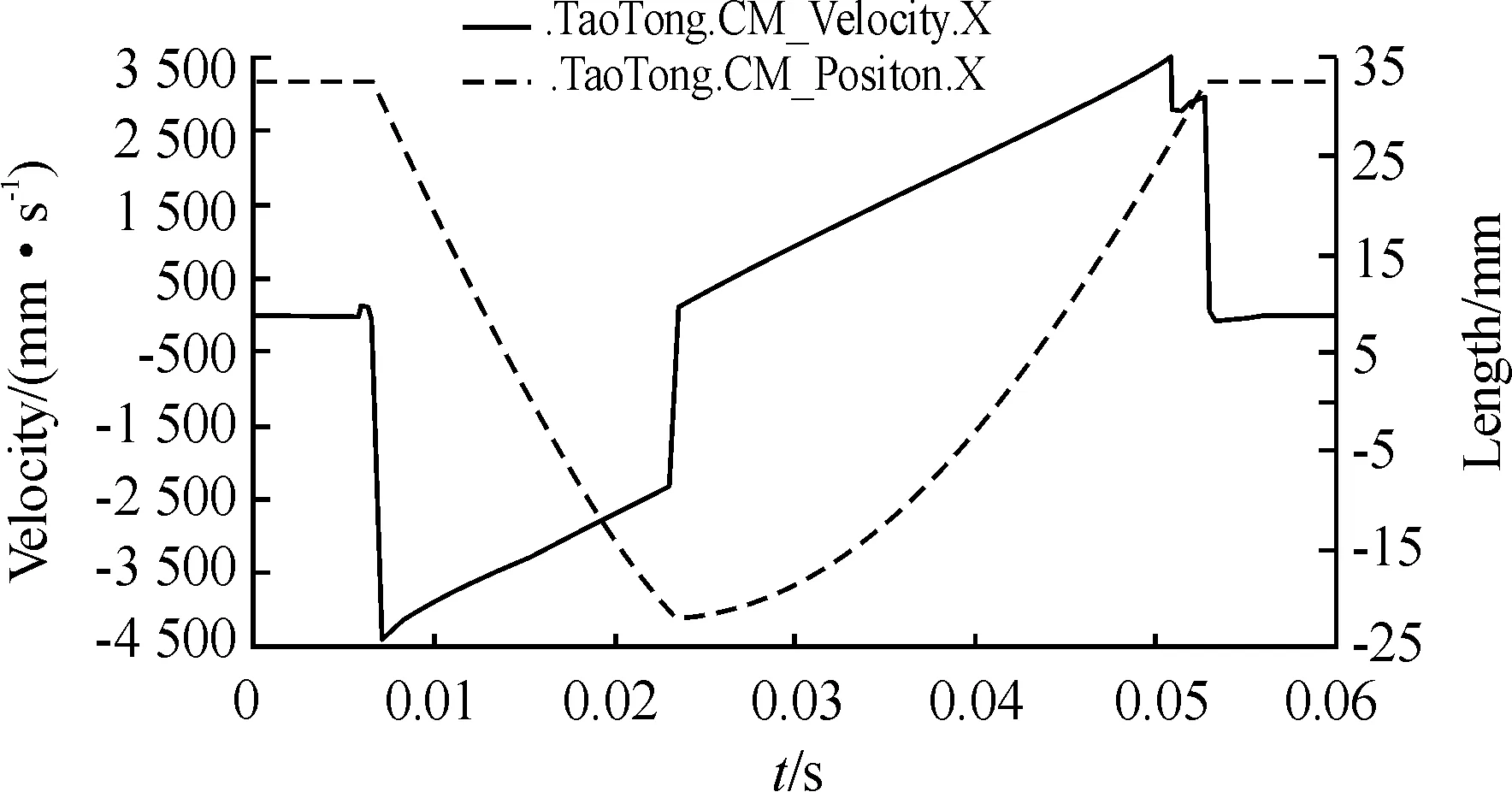
图8 套筒位移、速度曲线

图9 弹壳在抽、抛壳过程中的运动路径
由图8枪管、位移随时间变化的曲线可知:身管后坐时的最大速度为4.49 m/s,后坐到位的时间为0.008 4 s;复进到位时速度为2.83 m/s,复进到位的时间为0.052 9 s。
由图套筒位移、速度随时间变化的曲线可知:套筒后坐时的最大速度为4.41 m/s,后坐到位时的速度为2.26 m/s;复进时的初始速度为0.098 m/s,复进到位时的速度为2.96 m/s。整个自动循环过程持续了0.045 8 s。
图9为弹壳在抽、抛壳过程中的运动轨迹,从图中可以看出:弹壳在拉壳钩的作用下较平稳地运动到抛壳挺位置,在与抛壳挺撞击后,从抛弹窗翻滚地抛出。
5 结论
基于虚拟样机和有限元技术建立了手枪刚柔耦合模型,通过将仿真结果与试验作对比,证实了模型的合理性,为自动武器中的柔性件在ADAMS中仿真提供了思路,为该手枪进一步机构优化提供了理论依据。
