SEEMINGLY INJECTIVE VON NEUMANN ALGEBRAS*

Gilles PISIER

Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, USA E-mail: gilles.pisier@imj-prg.fr

Abstract We show that a QWEP von Neumann algebra has the weak* positive approximation property if and only if it is seemingly injective in the following sense: there is a factorization of the identity of M

Key words von Neumann algebra; injectivity; positive approximation property

A vonNeumann algebra M is called injective if there exists a Hilbert space H and an isometric normal*-homomorphism u:M →B(H) such that there is a projection P :B(H)→u(M) onto u(M) with ‖P‖ = 1, which by Tomiyama’s theorem (see [57]) is automatically a completely positive and completely contractive conditional expectation. Injective von Neumann algebras play a central role in operator algebra theory (see e.g. [57, 58]). Following the work of Connes [19], Choi and Effros [14, 16] proved that a C-algebra A is nuclear if and only if its bidual Ais injective. Injectivity is in some sense analogous to amenability for groups.Equivalently M is injective if and only if the identity Idadmits, for some H, a factorization of the form

where u: M →B(H) and v :B(H)→M are completely contractive maps. In fact, it suffices for injectivity to require u,v completely bounded (see Remark 1.4). The fundamental injective example is of course B(H) itself. The main non-injective example is the von Neumann algebra L(F) of a free group F with at least two generators. Actually, by known results (see [31])for any embedding L(F) ⊂B(H) as a von Neumann subalgebra there is no bounded linear projection onto L(F). Moreover when M = L(F) there is no factorization as above with u,v both completely bounded(see Remark 1.4). The initial motivation of this note is the observation that when M =L(F),the identity Idstill admits a factorization as above but with u merely a normal unital positive (linearly)isometric embedding and v still completely contractive. When this holds we say that M is “seemingly injective”. Actually, for this to hold it suffices to have such a factorization with u and v both positive, and u normal.

In Theorem 1.11,we show that this property characterizes the M’s that have a certain form of weak*positive approximation property(in short PAP).The latter was proved for M =L(F)in [11] following Haagerup’s well known work [28]. Our result can be viewed as analogous to the equivalence between injectivity and semidiscreteness (see [58, p. 173]). In [23, p. 12],Effros and Lance called“semidiscrete”the algebras M that have the weak*completely positive approximation property (in short weak* CPAP). Their paper contains many important forerunners of Connes’s later results on the equivalence of injectivity and semidiscreteness. Connes[19] proved the latter equivalence for factors and Choi and Effros [14] extended it to arbitrary von Neumann algebras. We develop further the parallelism between seemingly injective and injective in §6.

1 Main Result

Throughout this paper, we abbreviate “approximation property” by AP.

We start by introducing the weakening of injectivity, which is the center of interest of this paper:

Definition 1.1 We will say that a von Neumann algebra (or a dual operator space) M is “seemingly injective” if Idadmits, for some H, a factorization of the form

Remark 1.4 If u,v are both assumed completely bounded in (0.1) then M is injective(and here we do not need to assume u normal). This is due to Haagerup (see [52, Th. 23.7]together with[52,Cor. 22.19]),refining previous results by Christensen-Sinclair and the author independently showing that the existence of a completely complemented embedding M ⊂B(H)(as a von Neumann subalgebra)implies injectivity. See [52, §23.7]for more detailed references.We return to this topic in Remark 4.6.

Remark 1.5 We could also consider a variant with a constant c, and say seemingly cinjective if ‖v‖≤c. There is a natural notion of seemingly nuclear which we do not spell out involving the analogue of the completely positive AP. All this seems to deserve further study.

Remark 1.6 Let p be a projection in M. We may view pMp as usual as a von Neumann algebra with unit p. It is easy to check that if M is seemingly injective, so is pMp ⊕C(1-p).Moreover, if M is seemingly injective, so is any von Neumann (unital) subalgebra N ⊂M for which there is a unital positive (automatically c.p.) projection P : M →N onto N. By the last assertion in Theorem 1.11 “unital positive” can be replaced by “positive” in the preceding assertion. In particular pMp is seemingly injective.

Remark 1.7 One major dissemblance with injectivity is that it is unclear (and a priori unlikely to be true) whether the tensor product of two seemingly injective algebras N,M is seemingly injective, even if N = B(K) with K Hilbert. This is of course due to the fact that,unlike for c.p. maps, we cannot tensorize unital positive maps. Analogously, we do not know whether the commutant Mis seemingly injective if M is so.

Remark 1.8 Following[42, p. 275],given a constant c ≥1,an operator space Z ⊂B(H)is c-mixed injective if Z is the range of a projection P : B(H) →Z with ‖P‖ ≤c. With this terminology, any remotely injective von Neumann algebra M is isometric to a weak* closed subspace Z ⊂B(H) that is 1-mixed injective. Indeed, if (1.1) holds we can take Z = u(M)and P =uv.

We will use the weak expectation property(in short WEP)originally introduced by Lance.Recall that a C-algebra A is called WEP (resp. QWEP)if the inclusion i:A →Ainto its bidual factors via completely positive (in short c.p.) and completely contractive (in short c.c.)maps through some B(H) (resp. if it is a quotient of a WEP C-algebra).

Remark 1.9 Kirchberg proved that a von Neumann algebra M is QWEP if and only if there is (for some H) a u.c.p. map v :B(H)→M that is a metric surjection (i.e. v maps the open unit ball of B(H) onto the open unit ball of M). In particular, this shows the following.

Proposition 1.10 A von Neumann algebra M is seemingly injective if and only if there is (for some H) a u.c.p. metric surjection v :B(H)→M that admits a normal unital positive lifting u:M →B(H).

Our main result is as follows (see §2 for the definitions on the various forms of AP):

Theorem 1.11 The following properties of a von Neumann algebra M are equivalent:

(i) M is seemingly injective,

(ii) There is a net of integers n(α) and normal finite rank maps T:M →M of the form

such that u,vare both unital and positive (so that ‖u‖ ≤1, ‖v‖ ≤1), uis normal and T(x) = vu(x) →x weak* for any x ∈M (we then say that M has the matricial weak*PAP).

(iii) M is QWEP and there is a net (T) of normal finite rank unital positive maps on M such that T(x)→x weak* for any x ∈M (in which case we say that M has the weak*PAP).

Moreover,for M to be seemingly injective it suffices that there is a factorization of the form(1.1) with u normal and u,v both positive.

Remark 1.12 We do not know whether any M with the weak*PAP is QWEP,although the c.p. analogue holds. See [37] for an illuminating discussion on the latter assertion.

Remark 1.13 (On free groups) If G is a free group the metric AP for C(G) was discovered by Haagerup [28], as well as the existence of a sequence of completely contractive finite rank multipliers on the von Neumann algebra L(G) = C(G)that form a weak* approximation of the identity. Of course the completely positive analogue is excluded since it implies injectivity. Nevertheless, using very similar ideas, Haagerup and de Canni`ere [11, Th. 4.6]proved that there is a sequence of finite rank normal multipliers that are positive, unital and form a weak*approximation of the identity on L(G)(see also[36]for groups with property RD with respect to a conditionally negative definite length function). In fact they obtain, for any integer k ≥1 fixed in advance, a sequence of unital k-positive multipliers. By (iii) ⇒(i) this shows that L(G) is seemingly injective, and actually we can find a factorization with a u that is k-positive, unital and normal.

Remark 1.14 (On Jordan algebras) The ranges of unital positive projections P on B(H)(such as P = uv which projects onto u(M)) are described by Effros and Størmer in [25].They show that such ranges are Jordan algebras for the Jordan product defined by a ◦b :=P(ab+ba)/2. In the situation of Definition 1.1 the map u: M →P(B(H)) being isometric is a Jordan morphism, and hence satisfies P(u(x)u(y)+u(y)u(x))=u(xy+yx) for all x,y ∈M.

Perhaps, some version of Theorem 1.11 remains valid when M is only a unital JBW*algebra, for instance: if such an M is seemingly injective, does it have the weak* metric AP ?A variant of this question is as follows. Consider a unital weak* closed subspace Z ⊂B(H)which is the range of a unital contractive projection. Does Z have the weak* metric AP ?Perhaps one should consider the same question with B(H) replaced by a unital JBW* algebra satisfying some suitable variant of the weak* positive metric AP ?

Remark 1.15 Let M be seemingly injective as in Definition 1.1 with u normal unital positive and v unital c.p. Then it is easy to check that for any unitary U in M,since‖u(U)‖=1 and v(u(U))=U, u(U)must be in the multiplicative domain of v. See e.g. [52, §5.1]or[47]for background on multiplicative domains. It follows that u(M) is included in the multiplicative domain of v, and hence if P =uv, we have

Thus if we equip the range P(B(H)) (= u(M)) with the product defined by a ◦b := P(ab) as in [17, Th. 3.1], we find a copy of M.

Remark 1.16 The equivalence(i)⇔(ii)in Theorem 1.11 is analogous to the equivalence of injectivity and the weak* CPAP (also often called “semidiscreteness”) for von Neumann algebras. This is a celebrated result of Connes [19] and Choi-Effros [14] (see also [62] for an alternate proof). As mentioned by Connes [19, p. 104] part of his argument for injective ⇒semidiscrete is implicit in Effros and Lance’s[23,proof of Prop. 4.5]. More details on that kind of argument (that we also use below) can be found at least in the semi-finite case in [52, Th.8.12, p. 166] (where unfortunately the reduction to the semi-finite case is incorrect).

Remark 1.17(About“hyperfiniteness”) By Connes’s results[19],if M is a finite injective von Neumann algebra there is a net of completely positive normal unital finite rank projections(i.e. idempotent maps) T: M →M that tend pointwise weak* to the identity of M. One could wonder whether in the seemingly injective case the same holds with completely positive replaced by positive.

It is known (see [18]) that if we restrict to the non-nuclear and weak* separable case,all injective von Neumann algebras are isomorphic as Banach spaces. Actually any infinite dimensional injective operator system on a separable Hilbert space is isomorphic either to ℓor to B(ℓ) (see [54], and also [9] for a related result). Curiously, the same is true for the free group factors as in Remark 1.13, because of the following fact well known to specialists.

Proposition 1.18 If we restrict to the non-nuclear case, any von Neumann algebra M that is isomorphic (as a Banach space) to a complemented subspace of B(ℓ) is isomorphic (as a Banach space) to B(ℓ).

Fact (Decomposition method) Let B,M be Banach spaces such that each is isomorphic to a complemented subspace of the other. If we also assume B ≃ℓ(B) then M ≃B.

Applying this with B =ℓ(B) and M =B, we find B ≃ℓ(B). Then we can apply this again but with B =B and M unchanged. This yields the proposition.

We now include the proof of the above fact for the reader’s convenience. Assume that B,M,X,Y are Banach spaces such that B ≃M ⊕X and M ≃B ⊕Y. Since B ≃M ⊕X ≃B ⊕Y ⊕X, the isomorphism B ≃ℓ(B) implies B ≃ℓ(B ⊕Y ⊕X). By absorption (i.e.,since N ∪{0}≃N), we have

Since M ≃B ⊕Y, we conclude M ≃B.□

Corollary 1.19 The free group factors L(G) (or the factors described in Remark 1.13)are isomorphic (as Banach spaces) to B(ℓ).

Proof By Theorem 1.11 and Remark 1.3,L(G) is isometric to a complemented subspace of B.□

Remark 1.20 The assumption in Proposition 1.18 holds for any QWEP weak*separable M with the weak* BAP, meaning any M admitting a uniformly bounded net of finite rank maps tending weak* to the identity. See Remark 5.8.

For basic facts and undefined notions, we refer the reader to [57, 58] for operator algebras and to [24, 47, 51] for operator spaces.

2 Approximation and Lifting Properties

A Banach space X has the metric AP (in short MAP) if its identity Idis the pointwise limit of a net of finite rank contractions. If X is a dual space we say that it has the weak*MAP if there is such a net but converging pointwise to Idfor the weak* topology. Equivalently,assuming X = (X), this means that Xhas the MAP. Indeed, by local reflexivity the finite rank contractions on X may be assumed weak*continuous and, taking convex combinations,a pointwise weakly convergent approximating net of finite rank maps on Xcan be transformed into a norm convergent one.

An operator system X ⊂B(H) has the positive MAP (in short PMAP) if its identity Idis the pointwise limit of a net of finite rank positive contractive maps. If X is weak* closed in B(H) we say that X has the weak* PMAP if there is such a net formed of weak* continuous maps that converge pointwise to Idfor the weak* topology. In the particular case when X is a von Neumann algebra, the existence of a uniformly bounded net of positive normal finite rank maps tending pointwise weak*to the identity implies the weak*PMAP(see Lemma 5.11).If the net is formed of positive unital maps (as in Definition 2.1) these are contractive so the weak* PMAP is automatic.

To emphasize the parallel with the weak* CPAP of [23] we adopt the following definitions(it would be more precise to add “unital” to weak* PAP and weak* CPAP, but we choose to abbreviate):

Definition 2.1 We say that a von Neumann algebra M has the weak* PAP if there is a net of unital positive normal finite rank maps (T) that tend pointwise weak* to the identity on M.

We say that M has the matricial weak*PAP if in addition the maps(T)admit a matricial factorization as in (ii) in Theorem 1.11.

We say that M has the weak* CPAP (resp. matricial weak* CPAP) if in addition to the preceding properties the maps (T) (resp. u,v) are all c.p.

Remark 2.2 Let A be a C-algebra with a (self-adjoint 2-sided closed) ideal I so that A/I is a quotient C-algebra. Let q : A →A/I be the quotient map. We will denote by i: A →Athe canonical inclusion. It is well known that the bidual A(which is a von Neumann algebra) admits a decomposition as I⊕(A/I). In particular, there is a contractive lifting A/I→Aand a fortiori from A/I to A. The question whether,when A/I is separable, there is always a bounded (or even an isometric) lifting from A/I to A has remained open since the works of Andersen and Ando from the 1970’s. In the broader setting of M-ideals counterexamples are known (see [32]), but not for ideals in C-algebras. In §9 we propose an approach to this question based on the conjecture that there are QWEP von Neumann algebras that are not remotely injective.

We will use several facts due to Andersen[2,Th. 7](in the real linear setting)and Ando[3](in full generality), as follows. If A/I has the MAP and is separable there exists a contractive(and hence isometric) lifting r : A/I →A. More generally, if X ⊂A/I is a separable closed subspace with the MAP, the inclusion X ⊂A/I admits a contractive lifting r : X →A. In fact, Ando proved that any map T : X →A/I from a separable Banach space X that is the pointwise limit of a net of finite rank contractions from X to A/I admits a contractive lifting r :X →A, so that qr =T.

It seems to have remained open ever since Ando’s paper [3] whether this holds without the approximability assumption on A/I. This problem was studied in Ozawa’s PhD thesis [43](see also [44] and [41]).

If A/I is separable and has the PMAP, T.B. Andersen [2, Th. 7 (3)] proved that there exists a positive isometric lifting r :A/I →A. Moreover(see [2, Th. 7 (2)]), in the unital case if X ⊂A/I is a separable operator system with the PMAP, the inclusion X ⊂A/I admits a positive lifting r :X →A that is isometric on the self-adjoint elements of X. The proof consists in a reduction to the case when X is finite dimensional, which, incidentally, is sketched below in Lemma 2.6. By an elementary argument (see Lemma 2.5), one can obtain a unital positive lifting r :X →A.

Remark 2.3 The modern way to think of Ando’s theorem is through Arveson’s principle(see [5, p. 351]) that says that in the separable case pointwise limits of “nicely” liftable maps are “nicely” liftable. More precisely, assume given a separable operator system X and a net of maps u: X →A/I (A/I being a quotient C-algebra), if each uadmits a lifting in an admissible class (to be defined below) and converges pointwise to a map u : X →A/I then u itself admits a lifting in the same class.

A bounded subset F ⊂B(X,A) will be called admissible if for any pair f,g in F and any σ ≥0 in Ithe mapping

Then Arveson’s principle (see [5, p. 351]) says that for the topology of pointwise convergence on X we have

Actually we do not even need to assume F bounded if we restrict to the pointwise convergence on a countable subset of X.

Remark 2.4 In particular if X is finite dimensional,we do not need to assume F bounded.For instance, taking for F the class of positive maps, let X be a finite dimensional operator system. If a map u:X →A/I is the pointwise limit of maps that admit positive liftings, then u itself admits a positive lifting.

The classes of positive contractions, unital positive maps, unital c.p. maps, contractions(resp. complete contractions) are all admissible and in the latter case X can be an arbitrary Banach (resp. operator) space. More generally, for each fixed k ≥1, the class of unital kpositive maps on an operator system and that of k-contractions on an operator space(meaning maps u such that Id⊗u is contractive) are admissible.

The proof uses quasi-central approximate units in I. By this we mean a non decreasing net(σ) in the unit ball of Isuch that for any a in A and any b in I

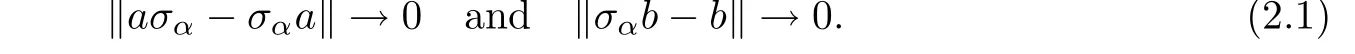
The reasoning is formally the same in all cases as can be checked in the presentations [21, p.266] or [51, p. 46 and p. 425]. Using this principle, one can reduce the lifting problem of an approximable map u:X →A/I roughly to that of lifting finite dimensional subspaces of A/I.

The next lemma is a simple well known fact describing how to obtain unital liftings when the map to be lifted is itself unital.

Lemma 2.5 Let E be an operator system and let u : E →A/I be a unital positive mapping. If there is a positive lifting r :E →A then there is a unital positive one r:E →A.

Proof Let (σ) be a quasi-central approximate unit in I. Let f be a state on E. Let r(x)=f(x)σ+(1-σ)r(x)(1-σ). Then r(1)-1=(1-σ)[r(1)-1](1-σ)and ris still a positive lifting. In particular q(r(1)) = 1. Since r(1) - 1 ∈I we have‖r(1)-1‖ →0 by (2.1). Choosing and fixing α large enough we may assume that r(1) is invertible. We then set for any x ∈E

The next Theorem 2.6 is the basic ingredient used in [2] by T.B. Andersen to prove that positive maps admit positive liftings when E is separable with the PMAP.

Theorem 2.6 (Vesterstrøm [60]) Let E be a f.d. operator system and let u : E →A/I be a unital positive mapping. Then u admits a unital positive lifting r : E →A (i.e. a map such that qr(x)=u(x) for any x ∈E).

In [53] Robertson and Smith give a quick direct proof of Theorem 2.6. Moreover, using an averaging argument their proof shows that, for any fixed n, Theorem 2.6 remains valid if“positive” is replaced by “n-positive” (see also [38] for a different argument).

3 Standard Forms

We call it normalized if s(1,1)=1.

To any normalized such form s we associate a state φdefined by φ(x)=s(1,x).

We will use the following basic property of the standard form.

Theorem 3.6 Let φ be a faithful normal state on a (σ-finite) von Neumann algebra M in standard form. Then the sesquilinear form sdefined for y,x ∈M by

Moreover, a form ψ ∈Msatisfies 0 ≤ψ ≤λφ (λ ＞0) if and only if there is a (uniquely defined) y ∈M with 0 ≤y ≤1 such that ψ(x)=λ〈ξ,JyJxξ〉 for all x ∈M.

See [52, Th. 23.30 p. 398] for detailed indications of the references.

We make crucial use of the following fact, for which the main idea goes back to Effros and Lance in [23, proof of Prop. 4.5].

We will also make use of the following fundamental property of self-polar forms due to Woronowicz and Connes.

See [52, Cor. 23.20] for details.

We will use the following consequence of Theorem 3.8.

Lemma 3.9 For any finite set (x) in a von Neumann algebra M, we have

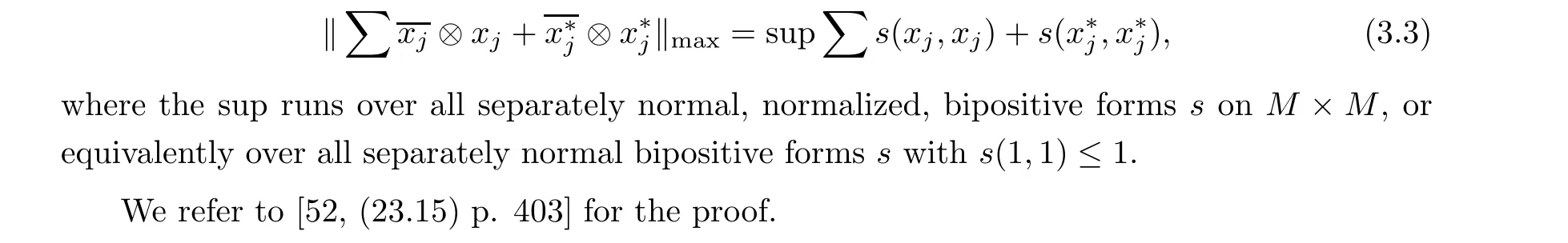
4 Pietsch-type Factorization

The next statement is a variation on the Pietsch-type factorization for oh-summing maps described in [50]. We say that an embedding j : B →B(H) has infinite multiplicity if H =

H ⊕H ⊕··· and j(b)=b ⊕b ⊕··· (b ∈B).

Proposition 4.1 Let B ⊂B(H)be an operator space embedded with infinite multiplicity and let(M,τ)be a tracial probability space. Let us denote by Cthe set of finite rank operators h ∈B(H)such that h ≥0 and‖h‖=1. Let v :B →M be a linear map such that v(b)=v(b)

Then using the fact that B is represented on H with infinite multiplicity one can obtain a net for which (4.7) holds (see e.g. [52, Prop. 4.23] for details).□

Moreover,if v is c.p. with ‖v‖≤1 then (4.5) holds for any (x) in B by Remark 4.2.

Remark 4.5 Let R and C denote as usual the row and column operator spaces. It is known(see[52,Rem. 22.20])that if v :B →D is such that‖Id⊗v :X⊗B →X⊗D‖≤1 both for X = R and X = C then v satisfies (4.3). Therefore, by Choi’s generalization of Kadison’s inequality ([12, Cor. 2.8]), any 2-positive contraction satisfies (4.3). Given this, the preceding lemma is not so surprising. In particular, any complete contraction v satisfies (4.3).See [52, Cor. 22.19] for a detailed proof.

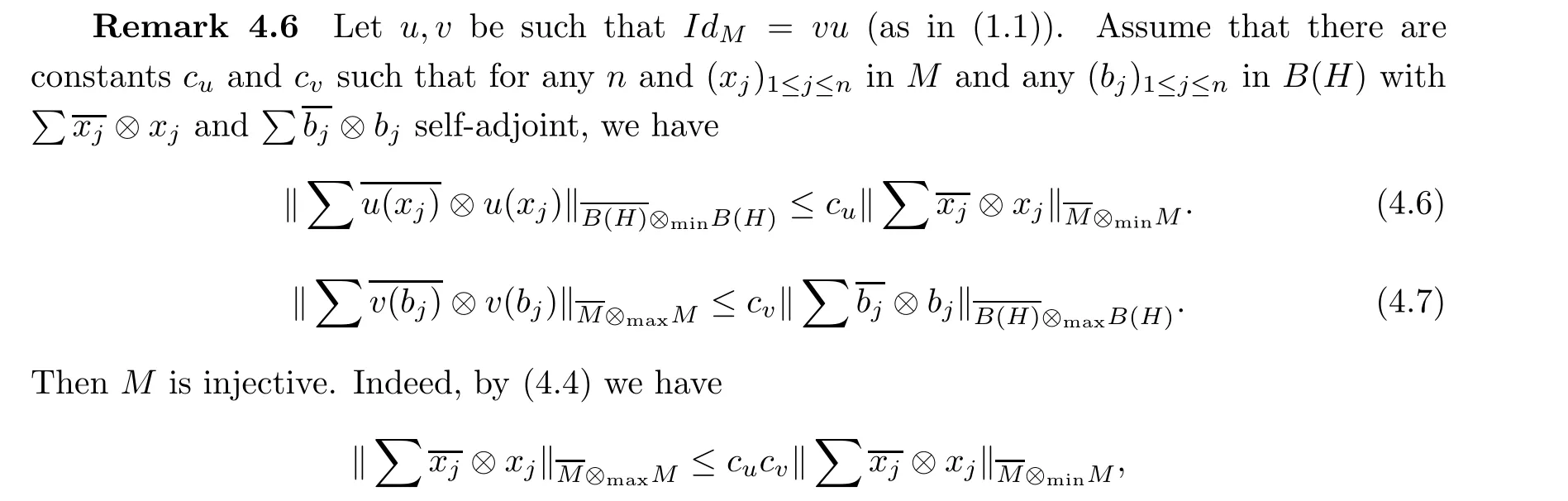
which by a theorem due to Haagerup (see [52, Th. 23.7]) implies that M has the WEP and hence (being a von Neumann algebra) that M is injective.

In particular this shows that if Id=vu with u c.b. and v c.p. then (4.6) and (4.7) hold(see Remark 4.2) and hence M is injective. Actually, much less suffices, as we now explain.

Let X be an operator space,for example R or C. Let us say that v :B →D is X-bounded if ‖Id⊗v :X ⊗B →X ⊗D‖＜∞. It is known (see [52, p. 375, Rem. 22.20]) that if v is X-bounded both for X = R and X = C, or equivalently for X = R ⊕C, then v satisfies(4.7) (the contractive case is discussed in Remark 4.5).

5 Proof of Main Result

We start by some simple preliminary elementary propositions.

Proposition 5.1 Let T : M →N be a linear map between von Neumann algebras.Assume that there is a net of pairs of positive contractions u:M →B(H),v:B(H)→N,with unormal, such that vu→T pointwise-weak*. Then there is (for some H) a pair of positive contractions u : M →B(H), v : B(H) →N, with u normal, such that vu = T. The construction is such that if the u’s and v’s are all unital then so are u,v, and if the v’s are all c.p. then so is v.

Proof Let B = ⊕B(H). Let u : M →B be defined by u(x) = ⊕u(x) (x ∈M).Let p: B →B(H) be the α-th coordinate mapping. We define v : B →N by setting v(b)=weak*limvp(b)=weak*limv(b) for any b=(b)∈B, where U is an ultrafilter refining the net. Clearly,vu=T and all the announced properties hold. Lastly, as the identity of B factors through B(H) with H = ⊕Hvia unital c.p. normal maps, we may replace B by B(H).□

The next lemma is elementary.

Lemma 5.2 Let u : M →B(H) and v : B(H) →M be positive maps (resp. with u normal). Let θ = vu : M →M. Let ε ＞0 and 0 ≤δ ＜1. If ‖θ(1)-1‖ ≤δ, there are unital positive maps u:M →B(H) and v:B(H)→M (resp. with unormal) such that

Since 1 - δ ≤η(1) ≤1 + δ + ε‖v(1)‖, we have ‖η- 1‖ ≤(δ + ε‖v‖)and ‖η‖ ≤(1+δ+ε‖v‖)≤2. The announced bound follows.□

Remark 5.3 Let M be a von Neumann algebra. Assume that we have a net of pairs of maps u:M →B(H), v:B(H)→M (here for convenience ε is used for the index of the net)such that the composition θ= vusatisfies ‖θ(1)-1‖→0 and θ(x) →x weak* for any x ∈M.

Note that this holds in particular if vu=Idindependently of ε.

Assume moreover that u, uare both positive, that sup‖v‖＜∞and that uis normal.Then there is a factorization Id=vu as in (1.1)with u normal and u,v both unital positive.Indeed, this follows from Lemma 5.2 and Proposition 5.1.

In particular,having Id=vuas in(1.1)with u,vmerely positive and unormal implies the existence of Id=vu as in (1.1) with u normal and u,v both unital positive.

Furthermore we will show at the end of the proof of Theorem 1.11 that the latter factorization implies that Idadmits the seemingly injective factorization of Definition 1.1.

As before, for any map u:A →M from a C-algebra to a von Neumann one we denote by¨u:A→M the canonical normal extension of u to A, so that ¨ui=u.

We next state an easy fact that will help us to relate our main topic to lifting problems.

Lemma 5.4 If a von Neumann algebra M is QWEP,there is a unital C-algebra W and a surjective unital *-homomorphism q :W →M that admits for some H a factorization of the form

where u is normal, finite rank with ‖u‖=‖T‖and v is a unital c.p. map (and hence ‖v‖=1).

If T is in addition unital positive, then we can ensure that u is also unital positive.

Proof Let W,q,w,wbe as in the preceding lemma. Let E = T(M) ⊂M = q(W).By Corollary 2.6 there is a contractive unital positive lifting r : E →W. Let u = wrT and v = w. Then since T is normal (resp. and unital positive) and dim(E) ＜∞the map u is normal (resp. and unital positive) with ‖u‖ ≤‖T‖, while v is u.c.p. and T = vu. The latter implies ‖T‖≤‖v‖‖u‖≤‖u‖.□

Before proving Theorem 1.11, we start by some preliminary remarks.

Remark 5.6 Consider the implication (i) ⇒(ii) in Theorem 1.11. By structural results we may assume that M is σ-finite. Indeed, by [57, Chap. 5, prop. 1.40] a general M is isomorphic to a direct sum of a family of algebras of the form M =B(H)¯⊗N with N σ-finite.For such an M, there is a net of projections (p) in M tending weak* to 1 such that pMpis σ-finite, or equivalently the unital subalgebra M= pMp⊕C(1-p) is σ-finite and is the range of a unital normal c.p. projection Qdefined by Q(x) = pxp+f(x)(1-p) where f is a normal state on M. Then Qtends pointwise weak* to Idand the range of each Qis σ-finite. Moreover, if M is seemingly injective, so is Q(M) by Remark 1.6. Thus to show that M has the weak* PAP it clearly suffices to show that each Q(M) has it, and the latter are σ-finite.

Remark 5.7 Consider again the implication (i) ⇒(ii) in Theorem 1.11. Assume M σ-finite. A tempting approach to prove this without using standard forms is to first prove this assuming M finite, from which the semi-finite case follows easily (using pMp for finite projections p), and then to invoke Takesaki’s duality theorem to pass from the semi-finite case to the general one. This roughly produces a general σ-finite algebra as the range of a unital c.p.projection on a semi-finite one. However since the latter projection is in general not normal,this route does not seem to go through to prove the weak* PAP. (We fell into that trap in a previous version of this paper.) In [62], to show that injectivity implies the weak* CPAP,Wassermann uses this path to prove that injectivity implies (iii) in Theorem 6.1 and then he relies on (iii) ⇒(i) in Theorem 6.1 (previously proved by Effros-Lance [23]). In the seemingly injective context, the analogue of the latter implication is what we are after, so this approach no longer seems to work. This explains our recourse to standard forms. Using the latter, we can give an argument covering the case of a general σ-finite algebra. Nevertheless, we include the finite case in the proof below because we feel it will be much easier for the reader to follow the general case after this warm up.

Proof of Theorem 1.11 Assume (i). Then M is isometric to a (Banach) quotient of some B(H) and hence is QWEP by Kirchberg’s results (see e.g. [45] or [52, Th. 15.5]). We will derive the matricial weak*PAP by the same kind of argument as the one which shows that injective von Neumann algebras have the weak* CPAP (see Remark 1.16 for references).

By Remark 5.6 we may assume that M is σ-finite.

We will first prove (i) ⇒(ii) in the finite case. Then in the second part of the proof we will show how the argument can be adapted to cover the general case using the standard form of M.

Thus we first consider a tracial probability space(M,τ). Let B(H),u,v be as in(1.1)with u,v both unital and positive (or equivalently unital and contractive). Let H = H ⊕H ⊕···.We may embed B(H)in B(H)acting diagonally with infinite multiplicity,and we have a unital c.p. projection from B(H) to this copy of B(H). By Proposition 4.1 (with B = B(H)) and Remark 4.4 we may assume that we have an ultrafilter U refining a net of finite rank operators h∈Csuch that for all b ∈B(H)

for any x ∈M, b ∈B(H) and hence denoting by j : M →Mthe canonical embedding we have V(b)-j(v(b)) →0 with respect to σ(M,M) or equivalently weakly in M. Passing to convex combinations of the V’s we may assume that ‖V(1)-j(1)‖→0 (and also that ‖V(b)-j(v(b))‖→0 for any b ∈B(H)). Assume for a moment that V(1)exists and lies in M. Then if we set

This shows that T(b) →v(b) for σ(M,M) and hence since M is dense in Mand (T) is equicontinuous, T(b)→v(b) for σ(M,M).

Now let H⊂H be the (finite dimensional) range of hand let p∈B(H,H) denote the orthogonal projection onto H. We define u:M →B(H) by setting u(x)=pu(x)p,and v(y) = T(pyp). Note that since pph= hpp= h, by (5.5) and (5.6) we have T(ppbpp) = T(b) for any b ∈B(H), and hence v(u(x)) = T(u(x)) for any

where v,u are unital positive contractions (and u is normal). Indeed, when x ∈M and (a)∈ℓ({M}), we may take u(x)=(u(x)) and v((a))=weaklimv(a) for some suitable ultrafilter U. It follows that M is isometric to a quotient Banach space of some B(H)and hence by a result of Kirchberg (see [52, Th. 15.5]) M is QWEP. Thus (ii) ⇒(iii).

For the last sentence in Theorem 1.11, suppose:

(i)’ We have Id=vu assuming merely that u and v are positive maps, with u normal.

Then, by Remark 5.3, Idhas a factorization as in (1.1) with unital positive u,v and u normal. A fortiori‖u‖=‖v‖=1. As we already observed,the mere positivity of v is enough to guarantee(5.2). But the latter was the only assumption needed on v to complete the preceding argument for (i) ⇒(ii). This shows (i)’ ⇒(ii) and hence (i)’ ⇒(i), and since the converse is trivial the proof is complete.□

Remark 5.8 The preceding proof of(iii)⇒(i)shows that any QWEP M with the weak*BAP is isomorphic to a complemented subspace of B(H). More precisely, in the weak* BAP case, Lemma 5.5 gives us a factorization as in (1.1) but in which the map u is merely bounded and normal.

We end this section with a characterization of the weak*PAP.It is not clear that it is really different from that of Theorem 1.11, because we do not know whether the weak* PAP implies QWEP, as is the case in the c.p. case for injectivity.

Theorem 5.9 Consider a σ-finite von Neumann algebra M ⊂B(H) in standard form.Let φ be a faithful normal state on M and let s be the associated self-polar form on M. The following are equivalent:

(i) M has the weak* PAP.

(ii) There is a net of bipositive, separately normal finite rank forms stending pointwise to s.

Proof Assume (i). Let (T) be a net of unital positive finite rank normal maps tending to Idpointwise weak*. Let s(y,x) = s(T(y),T(x)). Since s is separately weak* continuous, we have s(x,x) ≤lim inf s(x,x). (Indeed, we have by Cauchy-Schwarz |s(x,x)|=lim|s(x,T(x))|≤lim inf|s(x,x)||s(T(x),T(x))|.) Thus if U is an ultrafilter refining the net we have s(x,x) ≤s(x,x) with s(x,x) = lims(x,x). Since sis a bipositive normalized sesquilinear form we have s=s by Theorem 3.8 whence (ii).

Assume (ii). We will repeat the proof of the implication (i) ⇒(iii) in Theorem 1.11,so we just sketch the argument. We replace the net(s)by s(y,x)=(1+ε)(s(y,x)+εφ(y)φ(x)).Let φ(x) = s(1,x). We define the unit vector ξ∈Pby φ(x) = 〈ξ,xξ〉.Then, using Corollary 3.7,we define the unital positive(and hence contractive)finite rank map V:M →M by

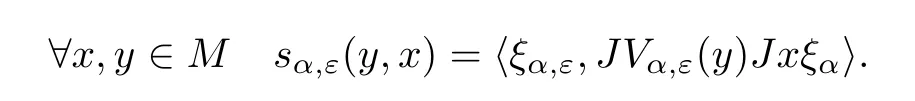
We have φ→φ weakly in M. Passing to convex combinations, we may assume that φ→φ in norm in M. By [27, Lemma 2.10]we have ξ→ξ in norm in H. This allows us to pass from lim〈ξ,JV(y)Jxξ〉=s(y,x) to

By (5.11)again we conclude that V(y)→y for the weak*topology of M,which yields(i). □

Remark 5.10 In [20], Connes and Jones studied an analogue of property (T) for a von Neumann algebra M. When M is equipped with a standard finite trace τ the latter property(T)is an obstruction to the existence of certain approximations of the identity on L(τ)formed of compact c.p. maps. More generally, in Theorem 5.9 if M has (T) then (ii) cannot hold if each bipositive form sdefines a compact c.p. map from M to M. We suspect that some examples of M with property (T) can be found that enjoy a stronger property ruling out the same for compact positive maps; such examples would then fail the weak* PAP.

For completeness, we record here the following simple fact.

Lemma 5.11 Let M be a von Neumann algebra. Assume that there is a uniformly bounded net of positive finite rank maps (T) that tend pointwise weak* to Id. Then M has the weak* PAP.

6 Comparison with Injectivity

Our goal here is to highlight the analogy of our results to the previous ones on injectivity and semidiscreteness, that came out of [19]. Connes’s ideas [19] also led to the equivalence of injectivity with approximate finite dimensionality (also called hyperfiniteness) and also with the weak* CPAP (also called semidiscreteness). Since we have no analogue of approximate finite dimensionality(see however Remark 1.17),for which we refer to chapter XVI in[58]or to[4, chap. 11], we will concentrate on the parallel between weak* CPAP⇔injective and weak*PAP⇔seemingly injective. We will focus on a result due to Effros and Lance from [23, Prop.4.5], with the refinement (i) ⇔(ii) proposed in [14].

Theorem 6.1 ([23]) The following properties of a von Neumann algebra M ⊂B(H) are equivalent:This fact a posteriori clarifies the equivalence between the weak* CPAP and (6.1), which boils down to (i) ⇔(iii) in Theorem 6.1. This was proved by Effros and Lance in [23] which circulated (in preprint form) before Connes and Choi-Effros proved in [16, 19] its equivalence with injectivity. At the time Effros and Lance proved that the weak* CPAP implies injectivity but could not prove the converse. After the Connes paper[19]it could be proved that injectivity implies (iii) in Theorem 6.1 (see [62]), and that gave the desired converse.

Theorem 6.2 Let M be a von Neumann algebra. The following are equivalent, where in(iii) we assume M σ-finite in standard form, and in (iii)’ we assume M finite with a faithful,normal and normalized trace τ.

where the sup runs over all H and all unital positive normal maps u:M →B(H).

Remark 6.5 In sharp contrast with the c.p. case, we do not know whether the weak*PAP implies the matricial weak*PAP,or equivalently whether the weak*PAP implies QWEP.

7 Counterexamples

Remark 7.2 Proposition 5.1 obviously remains valid if {B(H)} is replaced by a family{M} of seemingly injective von Neumann algebras.

Remark 7.3 This shows in particular that if M is seemingly injective then any von Neumann subalgebra M ⊂M admitting a unital positive (surjective) projection P : M →M is also seemingly injective. Note that when M is finite there is automatically a conditional expectation and hence a u.c.p. projection P :M →M.

where the N’s are σ-finite (=countably decomposable), the H’s are Hilbert spaces and ¯⊗denotes the(von Neumann algebra sense)tensor product. We claim that,under our assumption,any QWEP M is seemingly injective. Using Remark 7.2 we can reduce this to the case when I is a countable (or even finite) set and the H’s are separable (or even finite dimensional). In the latter case M is weak* separable, so the first part of the argument completes the proof of the claim. Since we know (by [56]) that M = B(H)contradicts this, our initial assumption does not hold.□

8 Remote Injectivity

We remind the reader that M is called remotely injective if we have a factorization as in(1.1) but where we only assume u normal and isometric, and v completely contractive. Let us first observe that this implies that M is QWEP. In fact it suffices for this to assume that u,v are both contractions. Indeed, this implies that Membeds isometrically into B(H), and hence that Mis finitely representable in B(H)and this implies by Kirchberg’s results (see[52, §15]) that M is QWEP.

The next statement gives a nice sounding reformulation of remote injectivity in terms of maximal operator spaces. The latter were introduced by Blecher and Paulsen [8] (see e.g. [51,§3] for more on this) . Given a Banach space X the operator space max(X)is characterized by the property that it is isometrically isomorphic to X and for any map u:max(X)→B(H) we have‖u‖=‖u‖. One way to produce a completely isometric realization of max(X)is like this:let C denote the collection of all contractions v :X →B(H) (with Heither of cardinality at most that of X or simply finite dimensional) and then consider the embedding

factors completely contractively through B(H) for some H.

Ozawa connected in[43]and[44]the lifting problems described in Remark 2.2 with maximal operator spaces in the sense of Blecher and Paulsen[8]and local reflexivity in the sense of Effros and Haagerup (see [24] or [51, §18]). Within operator spaces, it is convenient to introduce constants relative to these properties, as follows.

Definition 8.2 An operator space (o.s. in short) X ⊂B(H) is called λ-maximal if any bounded linear map u:X →Y into an arbitrary operator space Y is completely bounded and satisfies ‖u‖≤λ‖u‖.

For example for any Banach space X the o.s. max(X) described above is 1-maximal.

Definition 8.3 An o.s. X ⊂B(H)is called λ-locally reflexive if for any finite dimensional(f.d. in short)subspace E ⊂Xthere is a net of maps u:E →X with‖u‖≤λ that tend pointwise-weak* to the inclusion E ⊂X.

To make the link with Ozawa’s questions,we will use the following simple lemma. Whether an analogous lemma is valid with Y finite dimensional (possibly in some variant involving factoring the inclusion E ⊂X through Y) is the central open question discussed by Oikhberg in[41]. It is closely linked to Ozawa’s question whether all maximal spaces are locally reflexive.

Lemma 8.4 Let E ⊂X be a f.d. (or merely separable)subspace of a maximal o.s. There is a separable maximal subspace Y, such that E ⊂Y ⊂X.

Proof This is stated as Lemma 3.4 in [44]. For a detailed proof see Exercise 3.8 in[51,p.80], with solution in [51, p. 429]. The latter is based on Paulsen’s description of the unit ball of M(X) when X is maximal (see [46]or e.g. [52, p. 72]). This lemma can also be checked by a routine duality argument.□

An o.s. X has the OLLP if any complete contraction u : X →C/I into an arbitrary quotient C-algebra is locally liftable in the following sense: for any f.d. subspace E ⊂X there is a complete contraction u:E →C that lifts u.

Let us say that an o.s. X is strongly λ-maximal if X is the union of an increasing net of f.d.λ-maximal subspaces Esuch that X =∪E. In[43]and[44]Ozawa observed that any strongly 1-maximal X has the OLLP. Motivated by this observation, he asked whether any 1-maximal o.s. has the OLLP. By Lemma 8.4, the question reduces immediately to the case when X is separable. We think that the answer is negative and that there are 1-maximal o.s. that are not strongly λ-maximal for any 1 ≤λ ＜∞. In fact the space X = max(B(ℓ)) is a natural candidate for a counterexample. This question is related to our main topic via the following.

Proposition 8.5 Let M be a QWEP von Neumann algebra. If max(M) has the OLLP then M is remotely injective.

Let us say that a surjective *-homomorphism q : W →M (here between C-algebras)admits contractive (resp. bounded) liftings if for any separable Banach space Y and any contractive map u : Y →M there is a contractive (resp. bounded) map ˆu : Y →W that lifts u, meaning that qˆu = u. As discussed already in Remark 2.2 there are no known examples of surjective *-homomorphism q :W →M that fail this. This motivates the next statement.

Proposition 8.6 Let M be a QWEP von Neumann algebra. Let W be a WEP C-algebra and let q : W →M be a surjective *-homomorphism. If q admits contractive liftings then M is remotely injective.

Proof Let U :M →B(H) be as in the preceding proof. We again identify max(M) with U(M). By Lemma 8.4, for any f.d. E ⊂max(M) there is a separable Y ⊂max(M) such that E ⊂Y that is a maximal o.s. i.e. we have max(Y) = Y. Let u : Y →M be the inclusion map of Y into M. By our assumption, u admits a lifting ˆu : Y →W with ‖ˆu‖ ≤1. Then‖ˆu‖= 1 by maximality of Y. By the injectivity of B(H), the map wˆu admits an extension w: B(H) →B(H) with ‖w‖= 1. Let w= ww: B(H) →M. Note w(x) = u(x) = x for any x ∈Y, and a fortiori for any x ∈E. At this point we can conclude as in the preceding proof.□

The same argument shows that if q admits bounded liftings then the isometric embedding M ⊂B(H) is complemented, i.e. there is a bounded projection P :B(H)→M.

Remark 8.7 We failed to prove an analogue of Proposition 8.6 for positive contractive liftings to conclude that M is seemingly injective. We suspect the description in [48] of the analogue of max(X) when X is an operator system should be useful, but the analogue of the normal embedding U seems to be missing.

Remark 8.8 Let M be a QWEP C-algebra. Then there is a normal embedding M⊂B(H)with a unital completely positive projection from B(H)onto M(see [52, p. 207]),and the projection can be chosen normal by [52, p. 148]. If M is a von Neumann algebra there is a normal (non-unital) embedding M ⊂M(this is not the canonical one) with a unital completely positive normal projection from Monto M. Therefore we have a factorization

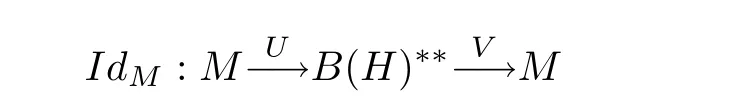
where U,V are normal unital c.p. maps. Thus, if B(H)was remotely (resp. seemingly)injective, the same would be true for any QWEP M.

Corollary 8.11 If max(B(H)) is 1-locally reflexive then B(H)is remotely injective.

Proof Indeed, B(H) is injective and hence has the WEP.□

9 Some Questions

By a well known result (see [14, 14]) a C-algebra is nuclear if and only if Ais injective.One could name “seemingly nuclear” the C-algebras A for which Ais seemingly injective.Unfortunately at this stage we do not have any valuable information on this notion.

Similarly, a discrete group G could be called “seemingly amenable” if M =L(G) is “seemingly injective”. By Remark 1.13 this would lead to the shocking assertion that free groups are seemingly amenable!

At the moment we do not have any example of a group that is not seemingly amenable but we suspect that such examples exist, for instance among property (T) groups (for which we refer the reader to [6]).

As for von Neumann algebras, it would be nice to exhibit more examples of M’s that are QWEP but not seemingly injective, without relying on Szankowski’s construction [56].

Another puzzling question is whether it is really essential that the map u in Definition 1.1 should be normal. It seems essential for the proof of Theorem 1.11. So we ask: does any QWEP von Neumann algebra M admit a factorization as in (1.1) with u isometric and ‖v‖=1 ? Is any non-nuclear QWEP von Neumann algebra M isomorphic as a Banach space to B(H) for some H ?

Unfortunately, we could not decide the following (which were our original motivation):

Conjectures:

(i) Any remotely injective von Neumann algebra M has the (Banach space sense) weak*MAP (equivalently Mhas the MAP).

(ii) B(H)(say for H =ℓ) is not remotely injective.

(ii)’ There is a QWEP von Neumann algebra that is not remotely injective.

(iii) There exists an ideal in a separable C-algebra with no contractive lifting, and hence with lifting constant ＞1.

We will show(i)⇒(ii)⇔(ii)’⇒(iii). Obviously(i)implies(ii)by Szankowski’s results on the failure of the AP for B(H) or a fortiori for any non-nuclear von Neumann algebra. Indeed,his results imply that B(H)fails the MAP, and hence that B(H)fails the weak* MAP. (ii)⇒(ii)’ is trivial since B(H)is QWEP (see [52, p. 205]). In fact (ii) and (ii)’ are actually equivalent by Remark 8.8.

The fact that (ii) implies (iii) follows from Proposition 8.6.

This argument shows that if (iii) fails then any QWEP M is remotely injective, or equivalently (ii) fails.

In conclusion,if there exists a QWEP von Neumann algebra M that is not remotely injective(which boils down to M =B(H)), then there exists an ideal in a separable C-algebra with no contractive lifting, and max(B(H)) is not locally reflexive (with constant 1). This would answer (at least for the constant 1 case) some of the questions raised in [43] and [44], and also in [41].

Lastly, we should mention that according to the recent very long preprint [35] there are von Neumann algebras that are not QWEP.