THE BEREZIN TRANSFORM AND ITS APPLICATIONS*

Kehe ZHU

Department of Mathematics and Statistics, State University of New York, Albany, NY 12222, USA

Abstract We give a survey on the Berezin transform and its applications in operator theory.The focus is on the Bergman space of the unit disk and the Fock space of the complex plane.The Berezin transform is most effective and most successful in the study of Hankel and Toepltiz operators.

Key words reproducing kernel; reproducing kernel Hilbert space; Hardy space; Bergman space; Fock space; Berezin transform; Toeplitz operator; Hankel operator;composition operator

1 Introduction

If H is a reproducing kernel Hilbert space on Ω and w ∈Ω,then by the Riesz representation theorem in functional analysis,there exists a unique function K∈H such that f(w)=〈f,K〉for all f ∈H. The function K :Ω×Ω →C defined by K(z,w)=K(z)is called the reproducing kernel of H.

If {e} is an orthonormal basis for the RKHS H on Ω, then it can be shown that

In particular, the reproducing kernel K(z,w) is independent of the choice of the orthonormal basis {e}. There are only a few cases where the formula above can be used to yield a closedform formula for K(z,w).

We assume that the RKHS in our discussion has the additional property that for every w ∈Ω there exists some f ∈H such that f(w)/=0. In this case, it is clear that

These are called the normalized reproducing kernels of H. It is easy to see that the set of all finite linear combinations of (normalized) kernel functions is dense in H.

In functional analysis, we often encounter linear operators induced by functions; these include pseudo-differential operators, Hankel operators, Toeplitz operators, and composition operators. The inducing function is usually called the symbol of the resulting operator. Conversely, in many situations, a linear operator on a Hilbert space H also gives rise to a function on Ω. For example, any square matrix A = A, which is a bounded linear operator on the finite dimensional Hilbert space C, generates a characteristic polynomial p(λ)=det(λI-A).In the infinite dimensional case, many other important functions can be constructed from the operator λI -A.

The Berezin transform was first introduced in [13, 14] as a tool in quantization [15-18].It has since found applications in many areas of mathematics and mathematical physics. See[6, 38, 44, 46, 47, 53, 65, 71, 77, 84, 85] for some expository work about the Berezin transform in mathematical analysis and[39,40, 48,50, 57,68,70,85]for some applications of the Berezin transform in quantization and mathematical physics. The purpose of this article is to give a brief survey of the mathematical theory of the Berezin transform, especially regarding its applications to operator theory. Our main focus will be on problems related to the Bergman space of the unit disk and the Fock space of the complex plane.

2 Hardy, Bergman, and Fock Spaces

Let D be the open unit disk in the complex plane C. We use T to denote the boundary of D. There are three canonical reproducing kernel Hilbert spaces we want to consider; these are defined on T, D, and C, respectively.

On the unit circle T, each function f ∈L(T,dt) has a Fourier expansion

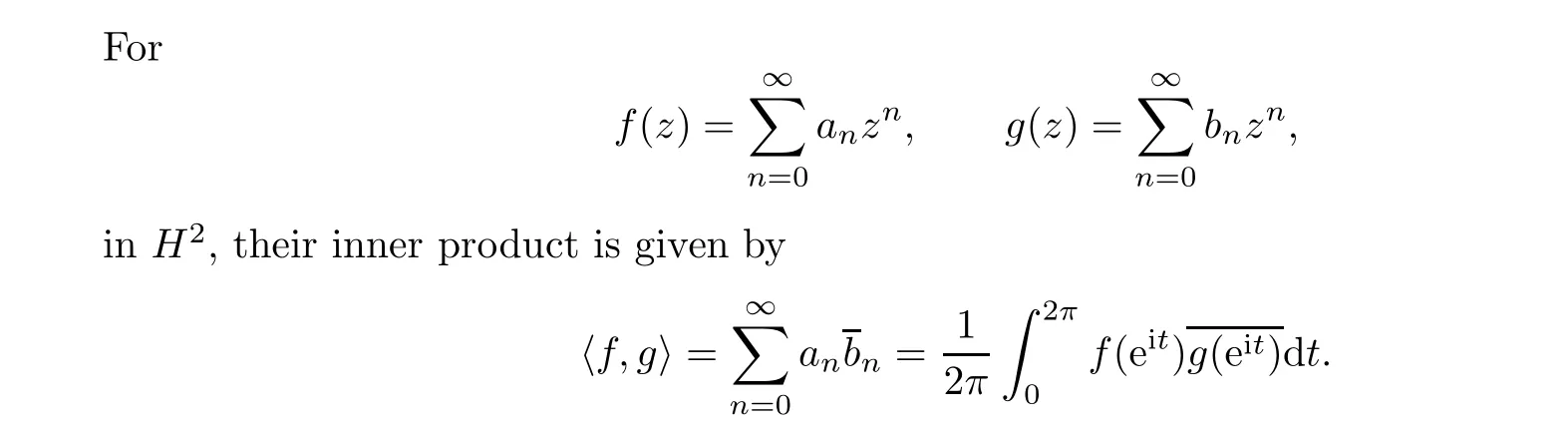
The experienced reader will have no trouble with us moving freely between the unit circle T and the unit disk D when we study issues involving the Hardy space H. Fortunately, there will be no such ambiguity when we study the Bergman space on D and the Fock space on C.

The Bergman space Ais the closed subspace of all analytic functions in L(D,dA), where

which is called the Bergman reproducing formula.

The Bergman space Ais a very popular and important setting for operator theory. See[84] and references therein for major developments in the past few decades. Despite the very simple definition, the function theoretic structure of the Bergman space Aremains mostly mysterious. This is in sharp contrast to the Hardy space H, where a mature function theory exists. The books [35, 46] contain the most noticeable progress in recent years regarding the function theory of Bergman spaces.

which is again called the reproducing formula for f. See [85] for an introduction to analysis on Fock spaces.

A common feature of the three analytic function spaces introduced above is that each of them is contained in an Lspace, so there is an orthogonal projection P from the containing Lspace onto the particular RKHS H. With the help of this projection, we can then define the notions of Toeplitz and Hankel operators on each of H =H,A,F. More specifically, for each of the three cases,there is also a corresponding space L(of the unit circle,the unit disk,the complex plane, respectively), and if φ ∈L, we define a linear operator T: H →H by T(f)=P(φf). Traditionally,Tis called the Toeplitz operator induced by φ, or the Toeplitz operator with symbol φ.

Similarly, for each φ ∈L, we can also define a linear operator H: H →L⊖H by H(f) = (I -P)(φf) = φf -P(φf), where I is the identity operator on L. We call Hthe Hankel operator induced by φ, or the Hankel operator with symbol φ. Since each orthogonal projection is an operator with norm equal to 1,we see that both Tand Hare bounded linear operators with ‖T‖≤‖φ‖and ‖H‖≤‖φ‖.

The integral representation for the orthogonal projection P : L→H allows us to extend the domain of P to a space much larger than L. For example, in the case of Hand A, the natural domain of P as an integral operator is L. With this extension of P,we can sometimes densely define Tand Hfor certain unbounded functions φ in the respective contexts. It is actually easy to produce examples of unbounded functions φ that will induce bounded operators Tand H(except the case of Toeplitz operators on H). In fact, if we use a symbol function φ ∈L, then the operators Tand Hare densely defined on H, with their domain containing the closed linear span of all normalized reproducing kernels which is dense in H.

The most successful application of the Berezin transform in operator theory occurs in the study of Hankel and Toeplitz operators, and this will be the focus of this survey. See [84, 85]for an introduction to Hankel and Toeplitz operators on Bergman and Fock spaces. We will not touch the subject of quantization, although that was the original physical motivation for the Berezin transform. Since the Berezin transform of an operator T : H →H is defined in terms of the normalized reproducing kernels, the following simple result is critical when we study compactness properties for operators on H:

To illustrate how the Berezin transform can be used in the study of operators on reproducing kernel Hilbert spaces, we begin with the following immediate consequence of Lemma 2.1:

In many situations, as we will see in the next few sections, the converse of the above is also true, but there are very simple examples to show that this is false in general. In fact, the operator T : A→Adefined by Tf(z) = f(-z) is clearly unitary (so not compact), but its Berezin transform

as |w|→1.

In addition to Toeplitz and Hankel operators(together,they are sometimes called Ha-plitz operators),we will also use composition operators as an important example. More specifically,if φ:D →D is an analytic self-map of the unit disk,we can define linear operators C:H→Hand C: A→Aby C(f) = f ◦φ. It follows from the classical Littlewood subordination principle that Cis bounded on both Hand A. See [84] for an introduction to composition operators on Hand A.

For an analytic self-map φ: C →C (namely, any entire function φ), we may also define a composition operator C: F→Fby C(f) = f ◦φ. Unfortunately, composition operators in this context are not always bounded, but it is known (and relatively easy to prove) exactly which entire functions φ induce bounded composition operators on F. We will not discuss composition operators on F.

3 The Classical Poisson Transform

We begin with the most classical example of the Berezin transform, namely, the Berezin transform associated with the Hardy space. Thus we take a function φ ∈L(T,dt)and consider the Toeplitz operator T:H→H. Since the normalized reproducing kernels of Hare given by

on D for any function φ ∈L(T,dt) without going through the notion of Toeplitz operators. In other words, we can define the Berezin transform of any function φ ∈L(T,dt) as the Poisson transform of φ.

As an application of the Berezin/Poisson transform on H, we obtain the following characterization of bounded and compact Toeplitz operators on the Hardy space:

Theorem 3.1 Suppose that φ ∈L(T,dt) and that Tis the densely defined Toeplitz operator on H. Then we have the following:

(a) Tis bounded on Hif and only if φ ∈L(T);

The simple result above is a good illustration of how the Berezin transform can be used to tackle problems in operator theory. We will consider two other similar applications: one involving Hankel operators and the other involving composition operators.

By Garcia’s Lemma (see [45]), f is in BMOA,the space of all analytic functions with bounded mean oscillation on the unit circle.

On the other hand, if f is in BMOA, we can write f = P(φ) for some φ ∈L(T). After the Poisson extension to D, we can write φ = φ+φ, where each φis analytic in D with φ(0)=0, which gives P(φ)=φ. It follows that φ=φ+f and H=H+H=H. This shows that His bounded with ‖H‖≤‖φ‖.

Therefore,with the help of the Berezin/Poisson transform and using some results from the theory of BMO, we are able to characterize all bounded Hankel operators on H. The same arguments also lead to a corresponding characterization for compact Hankel operators on H.Thus we have shown that, for f ∈H, the Hankel operator His bounded (or compact) on Hif and only if f belongs to BMOA (or VMOA). Since every function on T consists of an analytic part and a conjugate analytic part, we can restate the result above as follows:

4 The Berezin Transform for the Bergman Space

Let f ∈L(D) and consider the Toeplitz operator T:A→A. It is easy to see that the Berezin transform of Tis

which is easy to verify.

In the case of the Hardy space, the Berezin transform of a function f on T is simply the Poisson harmonic extension of f to the unit disk D. This, together with some classical results in complex/harmonic analysis, implies that T: H→His bounded ifff is bounded, and that T:H→His compact ifff =0. It is easy to see that this is no longer true for Toeplitz operators on the Bergman space. The difference stems from the fact that a function on the unit circle has a relatively simple structure (it consists of an analytic part and a conjugate analytic part), while a function on the unit disk is much more complicated (it has an analytic part, a conjugate analytic part, and a third component that is very difficult to describe).

Let φ ∈L(D,dA) be any unbounded function with compact support in D. It follows from the integral representation for T:A→A,

The result above is false in general without the positivity assumption. However, if we assume that the function f is already bounded,then the compactness part remains true without the assumption f ≥0.

The characterization of bounded and compact Hankel pairs Hand Hin terms of the Bergman metric BMO and the Berezin transform began in[81]and continued in[12]and many other papers.

We have now seen several natural and successful applications of the Berezin transform in operator theory, but the Berezin transform can also be studied as an operator itself. This is certainly the case for the Poission transform (i.e., the Berezin transform in the context of the Hardy space), which has been a classical tool in complex and harmonic analysis, independent of operator theory.

This shows that all (complex) harmonic functions in L(D,dA) are fixed-points of the Berezin transform. It turns out the converse is also true.

Theorem 4.6 Suppose that f ∈L(D,dA). Then Bf =f if and only if f is harmonic.

The characterization of fixed-points for the Berezin transform in the context of the Bergman space over the unit disk was an open problem for almost a decade before the theorem above was finally proved by Ahern, Flores, and Rudin in [2]. The characterization for Bf = f when f ∈L(D) was done earlier in [36]. Despite the extremely elementary and elegant statement of Theorem 4.6,its proof in [2] was highly non-trivial;a lot of complex analysis was carried out with the help of certain special functions and some numerical computations. This is another remarkable theorem regarding the Berezin transform.

The Poisson transform of any function f ∈L(T)is a harmonic function on D. The Berezin transform Bf of any function f ∈L(D,dA) is clearly real-analytic. It is natural to wonder what other regularity properties Bf may have. In other words,is there a way to determine the range of the Berezin transform? Some partial results can be found in [1, 66]. Here we mention a Lipschitz estimate for the Berezin transform of functions in BMO; see [12, 84].

Theorem 4.7 For any f ∈BMOwe have

for z,w ∈D, where β(z,w) is the hyperbolic metric (or Bergman metric) between z and w.

As an integral transform,we can certainly apply the Berezin transform iterately many times to a “reasonably good” function. In particular, Bf is well defined for any f ∈L(D) and any positive integer n. More generally, for any p ∈(1,∞), it can be shown that the Berezin transform B is a bounded linear operator on L(D,dA). Thus we can also consider Bf for f ∈L(D,dA), p ＞1, and n ≥1. A natural question then is this: is there anything we can say about Bf as n →∞? We mention one particular result in this direction; see [4, 84].

Theorem 4.8 Suppose that f ∈C(D). Then

Note that the result above is not true without some assumption on f. For example, if f(z)=log(1-|z|), then Bf is defined for all positive integers n. In fact, it is elementary to check that Bf = f +1, so Bf = f +n for every positive integer n. It is then clear that the sequence {Bf} does not converge. As a first step, we can ask to determine the convergence properties of {Bf} for a general function f ∈L(D).

The assumption that f be smooth with compact support in D can be relaxed somewhat,but the current form of the theorem is usually strong enough for applications and it follows easily from Green’s formula. We also mention that it is possible to express the Berezin transform as a function of the invariant Laplacian (see [65] for example).

5 The Berezin Transform for the Fock Space

is the fundamental solution of the heat equation. Any solution of the heat equation can be built from the fundamental solution using the heat transforms.

One of the reasons why the Berezin/heat transform plays a more prominent role in the theory of Fock spaces than its counterpart in the theory of Bergman spaces is that the heat transform has the following semi-group property (see [85] again):

Theorem 5.2 We have HH=Hfor all positive parameters s and t in the sense that H(Hf)=Hf for any f ∈L(C).

The assumption f ∈L(C) can easily be relaxed, but that is only a technical point which is not essential in most situations.

for all z,w ∈C.

where the supremum is taken over all arcs I in T with |I| being the dt-measure of I and fbeing the mean of f over I with respect to dt.

In the theory of Bergman spaces, we have a similar space BMO, which can be described either geometrially or in terms of the Berezin transform. Thus for the theory of Fock spaces,we define a space BMOconsisting of all functions f on C such that

It is easy to see that in each of the three cases above, Lis a proper subspace of the corresponding BMO space (on the unit circle, the unit disk, and the complex plane, respectively).The following result gives another Lipschitz estimate for the Berezin transform in the Fock space setting:

Theorem 5.4 For any t ＞0 there exists a positive constant C,depending on t only,such that

for all f ∈BMOand all z,w ∈C.

In a fashion similar to the Hardy and Bergman space settings,the Berezin transform is also a very useful tool in the study of Hankel and Toeplitz operators in the Fock space setting. In particular, we have the following two natural results:

We believe the first usage of the Berezin transform in the theory of Hankel and Toeplitz operators was in the Fock space setting (see [19, 20, 85]).

6 Sarason’s Toeplitz Product Problem

Finally,we mention a recent success story for the Berezin transform in the study of Ha-plitz operators. This concerns the following interesting problem raised by Donald Sarason in [67]:

Problem 6.1 Characterize analytic functions f and g on D such that the product TTof Toeplitz operators on Hor Ais bounded.

Although Sarason originally only asked the question for Toeplitz operators on the Hardy and Bergman spaces,it is clear that the problem also makes sense for Toeplitz operators on the Fock space. Note that the order of multiplication in TTis important. When Sarason raised the problem above, he also formulated the following conjecture in [67] in terms of the Berezin transform and provided a proof for the “only if” part:

More can be said on this; in fact, if the function in (b) or (c) above is bounded, then the same function must be constant (see [59] for more details).

Sarason’s original problem for Toeplitz products on both the Hardy and Bergman spaces remains unsolved. Although there is a very rich function theory for the unit disk, the analysis in the Fock space setting is easier because there is a prominent rigidity theorem on the complex plane (i.e., Liouville’s theorem) that helps us to determine bounded Toeplitz products, Hankel products, and mixed Ha-plitz products on the Fock space.