QUANTIZATION COMMUTES WITH REDUCTION,A SURVEY*

2021-02-23XiaonanMA

Acta Mathematica Scientia(English Series) 2021年6期

Xiaonan MA

Institut de Math´ematiques de Jussieu-Paris Rive Gauche, Universit´e de Paris, UFR de Math´ematiques, Case 7012, 75205 Paris Cedex 13, France E-mail: xiaonan.ma@imj-prg.fr

Abstract We review the themes relating to the proposition that “quantization commutes with reduction” ([Q,R]=0), from symplectic manifolds to Cauchy-Riemann manifolds.

Key words index theory; Dirac operator; geometric quantization

From September 1989 until July 1993,I was a student at the Sino-French mathematics class in Wuhan University founded by Professor Jiarong Yu. As a young person from the countryside,it was the most precious chance of my life, and the starting point of my mathematical career.I am very lucky to have witnessed Professor Yu’s great contribution to the development of modern mathematical education in China.

In this note,we will review some recent progress on the idea“Quantization commutes with reduction”,or briefly,that“[Q,R]=0”,which first appeared as the famous Guillemin-Sternberg conjecture for compact symplectic manifolds.

Note that the phase space of a classical mechanical system is a symplectic manifold. Geometric quantization,introduced in the 1960’s by Kostant and Souriau,gives a geometric method to properly quantize classical mechanical systems. To quantize a compact symplectic manifold,i.e., to associate a Hilbert space, we need a (prequantum) line bundle whose first Chern form equals the symplectic form.

Bott suggested that the Hilbert space appearing in the quantization should be the kernel of the Dirac operator acting on spinor bundles twisted by the line bundle. The way in which symmetries of the classical systems are reflected in the quantization has been formulated into the principle that “quantization commutes with reduction”.

Let (M,ω) be a symplectic manifold with a prequantum line bundle L. Assume that a compact connected Lie group G acts on M,and that the action lifts to L. Then the quantization of M should be a G-virtual representation, and it is interesting to determine the multiplicity of the irreducible representations of G.

The Guillemin-Sternberg conjecture that “quantization commutes with reduction” gives a precise geometric answer to this problem. By using the associated moment map when M is compact, roughly, they conjectured that the following diagram commutes:

New difficulties appear when the manifold M is no longer supposed to be compact,since in this case the index of the Dirac operator is not well defined. In her ICM 2006 plenary lecture,Mich`ele Vergne proposed to replace this by a certain transversal index introduced by Atiyah,under the natural hypothesis that the moment map is proper,and that the zero-set of the vector field induced by the moment map is compact. She conjectured that the idea that“quantization commutes with reduction” still holds in this case.

This note is organized as follows. In Section 1, we review the principle that “quantization commutes with reduction” in the symplectic case; in particular, we discuss our solution with Zhang [11, 12] on Vergne’s conjecture. In Section 2, we review our recent work with Hsiao and Marinescu [7], on the principle “quantization commutes with reduction” for Cauchy-Riemann(CR) manifolds. An important difference between the CR setting and the symplectic setting is that the quantum spaces in the case of compact symplectic manifolds are finite dimensional,whereas for the compact strictly pseudoconvex CR manifolds that we consider, the quantum spaces consist of CR functions and are infinite dimensional.

Due to space limitations, we only cite few references. One can find more comments, references and motivations in [9, 10] and [25].

1 Quantization Commutes with Reduction on Symplectic Manifolds

This Section is organized as follows. In Section 1.1, we recall the definition of the Dirac operator on an almost complex manifold and the Atiyah-Singer index theorem. In Section 1.2,we review the Guillemin-Sternberg conjecture for compact symplectic manifolds. In Section 1.3,we explain our solution to Vergne’s conjecture regarding noncompact symplectic manifolds. In Section 1.4, we give the refinement of [Q,R]=0 in the compact K¨ahler case.

1.1 Dirac operators

Let M be a manifold of real dimension 2n with a compatible almost complex structure J.We endow M with a Riemannian metric gcompatible with J, i.e., g(J·,J·)=g(·,·).Let (E,h) be a Hermitian vector bundle on M with Hermitian connection ∇and curvature R=(∇).

Let dvbe the Riemannian volume form of (T M,g). The L-Hermitian product induced by g,hon the space Ω(M,E) of smooth sections of Λ(TM)⊗E is given

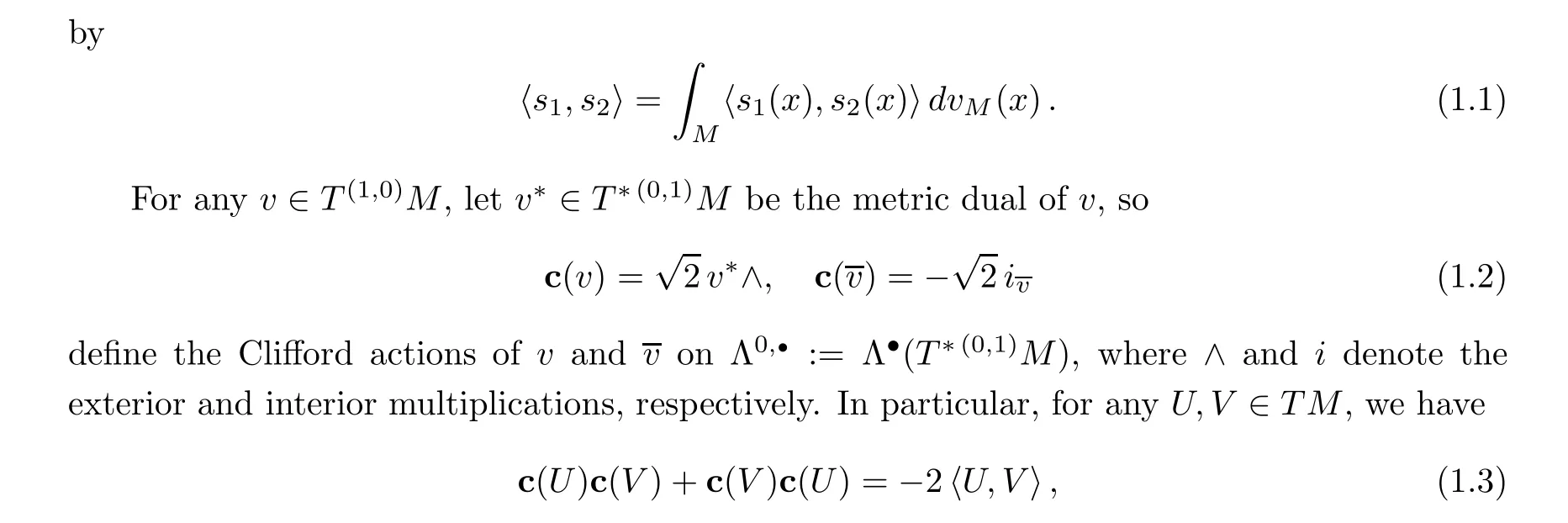
where 〈U,V〉 is the scalar product of U,V in (T M,g).

Consider the Levi-Civita connection ∇of (TM,g) with associated curvature R.Let ∇be the connection on TM induced by projecting ∇; ∇induces the connection ∇on det(TM) := Λ(TM). The Clifford connection ∇on Λis induced canonically by ∇and ∇(cf. [10, §1.3]). Finally, let ∇be the connection on Λ⊗E induced by ∇and ∇.

We recall briefly the construction of the Clifford connection ∇here. Let {w}be a local orthonormal frame of TM with dual frame {w}. Then

To explain the Atiyah-Singer index theorem which computes the virtual dimension of Q(E)by using characteristic numbers, we need to introduce first some characteristic classes. For any Hermitian (complex) vector bundle (F,h) with Hermitian connection ∇and curvature R

1.2 Quantization commutes with reduction

We explain now the idea of the geometric quantization introduced by Kostant [8] and Souriau [21].

Let (M,J,ω) be a compact symplectic manifold of real dimension 2n with a compatible almost complex structure J, i.e., g=ω(·,J·) is a J-invariant metric on TM.

Let (L,h) be a Hermitian line bundle over M endowed with a Hermitian connection∇with curvature R= (∇). We assume that (L,h,∇) satisfies the prequantization condition, that is, that In this case, we say that (L,h,∇) is a prequantum line bundle on M.

Let G be a compact connected Lie group with Lie algebra g. We assume that G acts on the left on M and that this action lifts to L. Moreover, we assume that G preserves g, J,hand ∇.

It is not easy to read offQ(L)directly from the Atiyah-Bott-Segal-Singer equivariant index theorem for its character. Guillemin and Sternberg [4] suggested a geometric way to compute Q(L)by using the associated moment map.

Definition 1.3 The moment map μ:M →gis defined by the Kostant formula [8]By the classical shifting trick (i.e., by working on M×O, where O=G·γ is the orbit of the co-adjoint action of G on g), we only need to prove (1.14) for γ =0.

This conjecture was proved by Meinrenken [14] and Vergne [24] when G is abelian, and by Meinrenken[15]and Meinrenken-Sjamaar[16]for non-abelian groups G,by using the symplectic cut technique of Lerman.

Tian and Zhang [22] gave an analytic proof of the Guillemin-Sternberg conjecture using a deformation of the Dirac operator which is associated with the function |μ|, and also the analytic localization technique in the local index theory developed by Bismut-Lebeau[3]. Their approach works for a general vector bundle E satisfying certain positivity conditions[22,(4.2)](used afterwards by Paradan [17, p.445]), and also for manifolds with boundary [23]. Paradan[17]developed later a K-theoretic approach by making use of the theory of transversally elliptic operators; see [25] for a survey and complete references on this subject.

1.3 [Q,R]=0: the noncompact case

Note that the most difficult part of the proof of Theorem 1.4 is to show that the shifting trick(i.e.,by working on M×Oto reduce to the case γ =0)still works in the current situation.

A new twist was introduced by Paradan and Vergne [20], who considered so-called spin quantization and established a version of [Q,R] = 0 in the compact setting. Hochs and Song[6] then established a version of [Q,R]=0 in the noncompact setting along the lines of [12].

Thus the next natural step is to consider [Q,R]=0 for noncompact groups and manifolds.Such a generalization is relevant to physics, since most classical mechanical phase spaces are noncompact, and to representation theory, since the representation theory for noncompact groups is much more intricate than for compact groups. Besides the problem of how to define the index,we need to work on the multiplicities of an infinite dimensional irreducible representation of G (Cf. [5, 13] and their recent works for the progress in this direction).

1.4 [Q,R]=0: the K¨ahler case

Let J,ω,h,∇be the objets on Minduced by J,ω,h,∇on M as in Section 1.2.

Theorem 1.5 If G acts freely on μ(0),then(M,J,ω)is also a K¨ahler manifold,and(L,h) is a holomorphic Hermitian line bundle over M, and ∇is the Chern connection on (L,h).

2 Quantization Commutes with Reduction on CR Manifolds

This Section is organized as follows. In Section 2.1, we recall in detail the definition of Cauchy-Riemann manifolds. In Section 2.2,we explain an important example of CR manifolds:the circle bundle of a holomorphic line bundle on a complex manifold. In Section 2.3,we present our recent work [7] on [Q,R]=0 for CR manifolds.

2.1 CR manifolds and CR functions

Let (X,TX) be a compact, connected and orientable Cauchy-Riemann (CR) manifold of dimension 2n+1, n ≥1, where TX is a CR structure of X; that is, TX is a complex vector sub-bundle of rank n of the complexified tangent bundle CTX :=TX ⊗C satisfying

A CR manifold X is said to be strictly pseudoconvex if, for every x ∈X, the Levi form Lis positive definite (negative definite). By (2.6) we see that the definition does not depend on the choice of the characteristic 1-form ω. By a change of sign of ωwe can and shall assume in the sequel that the Levi form is positive definite. If X is strictly pseudoconvex,then ωis a contact form and the Levi distribution HX is a contact structure.

Let T ∈C(X,TX) be a vector field, called characteristic vector field, such that

Note that in contrast to holomorphic functions, a CR function does not even need to be continuous. Here is a trivial example: consider a compact complex manifold M, such that X = S×M is a compact CR manifold with the CR structure defined by TM. Now a function f on X is CR if and only if there is a function h on the circle Ssuch that f(t,m)=h(t)for any t ∈S, m ∈M.

2.2 An important example: Grauert tube

2.3 [Q,R]=0 on CR manifolds

Let (X,HX,J) be a compact connected and orientable CR manifold of dimension 2n+1,n ≥1, and let ωbe a characteristic 1-form.

Let G be a d-dimensional compact Lie group with Lie algebra g. We assume that G acts smoothly on X and that the G-action preserves J and ω.

Definition 2.1 The moment map associated to the characteristic 1-form ωis the map μ:X →gdefined by

Let ι : Y := μ(0) →X be the natural inclusion and let ι: Ω(X) →Ω(Y) be the pull-back of differential forms by ι. Let π :Y →Y/G be the natural projection.

Theorem 2.2 If G acts freely on Y = μ(0) and the Levi form is positive on μ(0),then the reduced space X=Y/G is a strictly pseudoconvex manifold with contact form ωsatisfying ιω= πω. Moreover, we can choose the characteristic vector field T (cf. (2.7),(2.8)) such that T|∈C(Y,TY) and T is G-invariant.

The space Xis called the CR reduction. Under our hypotheses, if dim X≥3, Xis a strictly pseudoconvex CR manifold with characteristic 1-form (in this case also the contact form)ωinduced canonically by ω. If dim X=1,then each of the finitely many components of Xis diffeomorphic to a circle.

We will mainly work in the following setting:

This operator σcan be thought as a Guillemin-Sternberg map in the CR setting. It maps the “first quantize and then reduce” space (the space of G-invariant Sobolev CR functions on X) to the “first reduce and then quantize” space (the space Sobolev CR functions on X).

Under Assumption 2.3 (i), the hypothesis that dim X ≥5 is used in order to have local subelliptic Sobolev estimates on the set where the Levi form is positive definite and leads to the fact that the G-invariant Kohn Laplacian has closed range in L. Note also that the Kohn Laplacian on strictly pseudoconvex CR manifolds of dimension greater than or equal to five always has closed range in Lbut this is not true for all three dimensional strictly pseudoconvex CR manifolds.

We turn now our attention to Sasakian manifolds. Let(X,TX)be a compact connected Sasakian manifold,i.e.,the metric cone(C(X)=R×X,dr+rg)is a K¨ahler manifold. We fix a contact form ωand an associated Reeb vector field R (defined by iω=1, idω=0).

We assume that