L2 extensions with singular metrics on Kähler manifolds

In[11],Demailly proved an Lextension theorem for holomorphic line bundles with smooth metrics on weakly pseudoconvex K¨ahler manifolds. In [36], Yi proved an Lextension theorem for line bundles with singular metrics on compact K¨ahler manifolds,where the singular metrics are required to have analytic singularities or have trivial multiplier ideal sheaves when restricted to certain submanifolds. In [20], Guan and Zhou proved several general and unified optimal Lextension theorems with singular metrics on almost Stein manifolds, including projective manifolds and projective families (see [46] and [6, 17-19] for earlier results). In [7], Cao proved an optimal Lextension theorem with singular metrics on weakly pseudoconvex K¨ahler manifolds.In[14], Demailly proved several general Lextension theorems with singular metrics on weakly pseudoconvex K¨ahler manifolds. In [41] (see also [42]for a more general result), we established a method for proving an optimal Lextension theorem with singular metrics on weakly pseudoconvex K¨ahler manifolds (see also [37] for an earlier result with smooth metrics). The key step in our proof is the discovery of the generalized Siu’s lemma (formally formulated later on in [38]) for plurisubharmonic weights with nontrivial multiplier ideal sheaves. Our proof of the generalized Siu’s lemma is based on the strong openness property of multiplier ideal sheaves(conjectured by Demailly in [12] and [13] and by many others, and solved in [21]). The reader is referred to [43] for further studies on the generalized Siu’s lemma. These studies on the generalized Siu’s lemma constitute a key element of the proofs of our main results outlined in the present paper, being combined with many known ideas, results and techniques.

In [3], Berndtsson and P˘aun proved the log-plurisubharmonicity of the fiberwise Bergman kernel with singular metrics for projective fibrations (see [1] for earlier results with smooth metrics). In[20,22],Guan and Zhou found the optimal Lextension theorem and its geometric meaning, and consequently gave a new proof of this result. One can use this new method to prove the log-plurisubharmonicity of the fiberwise Bergman kernel in the K¨ahler case as an application of optimal Lextension theorems with singular metrics in the K¨ahler case.

In [4] (see also [5]), Berndtsson and P˘aun established an iteration method to obtain Lextension theorems (0 ＜q ＜2) from Lextension theorems, where the constants in the final estimates are consistent. One can use this iteration method to obtain optimal Lextension theorems (0 ＜q ＜2) with singular metrics in the K¨ahler case from optimal Lextension theorems with singular metrics in the K¨ahler case (the reader is referred to [20] for projective cases, and to [7, 41, 43] for general K¨ahler cases).

The positivity of twisted relative pluricanonical bundles and their direct images with singular metrics for projective fibrations was proved in [3, 5] and[31]. The positivity of the direct images of twisted relative canonical bundles with multiplier ideal sheaves for projective fibrations was proved in [23] by using the optimal Lextension theorem and its geometric meaning.The positivity of twisted relative pluricanonical bundles and their direct images with singular metrics in the K¨ahler case was discussed in [7, 41] and [43] with the applications of optimal L(0 ＜q ≤2) extension theorems with singular metrics in the K¨ahler case.

In the 1990s, applying the Ohsawa-Takegoshi Lextension theorem, Siu proved a lower limit property about integrals of plurisubharmonic weights with trivial multiplier ideal sheaves;this was called Siu’s lemma in [32]. In [43], by developing the method established in [41], we proved a general version of Siu’s lemma for plurisubharmonic weights with nontrivial multiplier ideal sheaves (see also [38] for an earlier result), and used it to prove a refined optimal Lextension theorem with singular metrics in the K¨ahler case. As an application, we gave a positive answer to a comparison question posed by Berndtsson-P˘aun [5] and P˘aun-Takayama[31] about singular metrics of twisted pluricanonical bundles.

In [8], Cao, Demailly and Matsumura proved an extension theorem for cohomology classes from non-reduced analytic subspaces in holomorphically convex K¨ahler manifolds (see also[14]for an earlier result on compact K¨ahler manifolds), where the defining function of the subspace is assumed to have neat analytic singularities. They asked whether this assumption can be replaced by arbitrary singularities. In [45], we gave a positive answer to this question. As applications,we unified a few well-known injectivity theorems and proved a vanishing theorem.We also obtained an optimal Lextension theorem for holomorphic sections defined on analytic subvarieties which generalizes and optimizes a general Lextension theorem in [14].

2 Preliminaries

Let us first recall some definitions and notations (see [9, 13, 14, 28, 29, 34], etc.).

Let X be a complex manifold. A function ψ : X -→[-∞,+∞) is said to be quasiplurisubharmonic (quasi-psh) if ψ is locally the sum of a plurisubharmonic (psh) function and a smooth function.

ψ is said to have neat analytic singularities if every point x ∈X possesses an open neighborhood U on which ψ can be written as

where U is an open coordinate neighborhood of x, and dλ is the Lebesgue measure.I(ψ) is just the usual multiplier ideal sheaf I(ψ).

In terms of the singular metric h of L, we will denote I(ψ) (k is a positive integer) by the global notation I(h), where ψ is the local weight of h. We also write I(h) as I(h) for simplicity.

The following result is the Ohsawa-Takegoshi Lextension theorem (a version on Stein manifolds was established in Section 3 in [30]):

Theorem 2.1 ([30]) Let Ω be a bounded pseudoconvex domain in C, let φ be a psh function on Ω, and let s be a holomorphic function on Ω. Let

where dVis the volume form on H induced from the Euclidean metric on C, and dλis the 2n-dimensional Lebesgue measure.

Now we recall some of the results used in the proofs of extension theorems with singular metrics in the K¨ahler case.

The following result is an Lexistence theorem for solving ¯∂equations with error terms:

Theorem 2.2 (Remark 3.2 in [11], Remark 12.5 in [13], Proposition 3.12 in [14]) Let(X,ω)be a complete K¨ahler manifold equipped with a(not necessarily complete)K¨ahler metric ω, and let (Q,h) be a holomorphic vector bundle over X equipped with a smooth metric h.Assume that τ and A are smooth and bounded positive functions on X and let

where C is the same constant as in the Ohsawa-Takegoshi Lextension theorem, dVis the volume form on H induced from the Euclidean metric on C, and dλis the 2n-dimensional Lebesgue measure.

The following result is the strong openness property of multiplier ideal sheaves for psh functions:

Theorem 2.5 (Theorem 1.1 in [21]) Let p ∈(0,+∞). Let φ be a psh function on the unit polydisk Δ⊂C. Assume that F is a holomorphic function on Δsatisfying

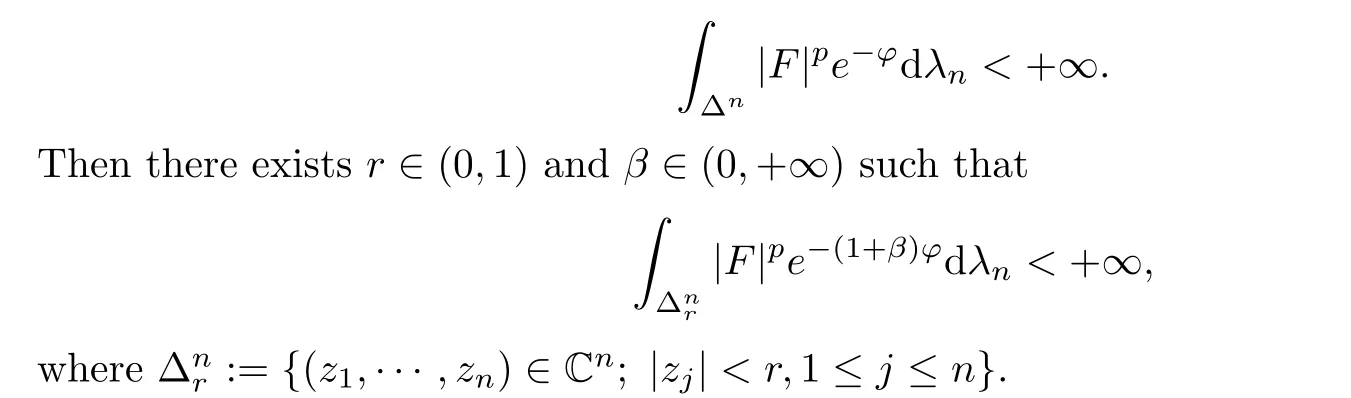
3 An Optimal L2 Extension Theorem with Singular Metrics in the K¨ahler Case

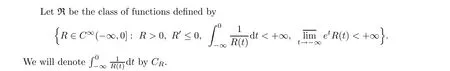
In [41], we established a method to prove the following optimal Lextension theorem with singular metrics on weakly pseudoconvex K¨ahler manifolds(one can also see[36]and[7,14]for some related results):

Theorem 3.1 Let R ∈ℜ. Let (X,ω) be a weakly pseudoconvex complex n-dimensional manifold possessing a K¨ahler metric ω, let φ be a plurisubharmonic function on X, let E be a holomorphic vector bundle of rank k over X equipped with a smooth metric h(1 ≤k ≤n),and let s be a global holomorphic section of E. Assume that s is transverse to the zero section,and let

Unlike the case of Stein or projective manifolds, a difficulty arose when one dealt with singular metrics of holomorphic line bundles on weakly pseudoconvex K¨ahler manifolds, since there is a loss of positivity in the regularization process of singular metrics on such manifolds(see Theorem 2.3).

In order to overcome this difficulty we need to use Theorem 2.3 and the error term method of solving ¯∂equations (see Theorem 2.2), and we also need to construct local holomorphic extensions satisfying a key limit property for Lintegrals of singular metrics; i.e., roughly speaking, we need to consider the following limit problem:

If φ is continuous, the conclusion of Problem A is obvious. The difficulty to obtain a holomorphic extension with such a limit property comes from the case when φ is a general plurisubharmonic function with arbitrary singularities.

Such a limit property is some kind of generalized Siu’s lemma for psh weights with nontrivial multiplier ideal sheaves on the center fiber. The original Siu’s lemma concerns those psh weights with trivial multiplier ideal sheaves on the center fiber (we will discuss Siu’s lemma and its generalizations more explicitly in Section 4).

In [36], Yi used a version of the original Siu’s lemma as one of the key tools to obtain an Lextension theorem on compact K¨ahler manifolds in the case in which the singular metric h of L has a trivial multiplier ideal sheaf when restricted to Y.

In[41],by constructing a family of holomorphic extensions with some kind of estimate rather than a fixed holomorphic extension, we obtained a limit property similar to the conclusion of Problem A (see Proposition 3.2). Then, by using this limit property and the strong openness property of multiplier ideal sheaves(see Theorem 2.5)as the key tools,we overcame the difficulty in dealing with singular metrics in the proof of Theorem 3.1.

The log-plurisubharmonicity of the fiberwise Bergman kernel for projective fibrations was proved in [1] in the smooth metric case, and in [3] in the singular metric case. In [20],Guan and Zhou discovered a relation between the optimal Lextension theorem and the logplurisubharmonicity of the fiberwise Bergman kernel, and consequently gave a new proof of Berndtsson’s and Berndtsson-Paun’s results. As another application of Theorem 3.1 and the method in [20], one can prove the following log-plurisubharmonicity of the fiberwise Bergman kernel in the K¨ahler case (see [7] and [41]):

Theorem 3.4 Let Π : X →Y be a surjective proper holomorphic map from a K¨ahler manifold X of dimension n to a complex manifold Y of dimension k. Denote by Ythe set of points which are not critical values of Π in Y. Set X=Π(Y). Let L be a holomorphic line bundle on X equipped with a singular metric h such that

(i) the curvature current of (L,h) is semipositive on X;

(ii) H(X,K⊗L|⊗I(h|))/=0 for some point y∈Y.

Then the logarithm of the fiberwise Bergman kernel of the line bundle (K⊗L)|is plurisubharmonic on X, and hence it defines a singular metric on (K⊗L)|with semipositive curvature current, which is called the fiberwise Bergman kernel metric. Furthermore,this metric extends across XXto a metric with semipositive curvature current on all of X.

The extension in Theorem 3.1 is from submanifolds. In [42], we discussed the extension from subvarieties and proved an optimal Lextension theorem for holomorphic line bundles with singular metrics to weakly pseudoconvex K¨ahler manifolds that optimizes one of the main theorems in [14] (see Theorem 2.8 and Remark 2.9 in [14]). The key ideas in [42] for dealing with singular metrics are similar to those in [41], so we will not discuss them here.

4 Siu’s Lemma and a Refined Optimal L2 Extension Theorem with Singular Metrics in the K¨ahler Case

As shown in Section 3,the limit property we obtained in the proof of Theorem 3.1 concerns a family of holomorphic extensions,while the limit property in Problem A concerns the existence of one fixed holomorphic extension. It is interesting to study Problem A further. To begin with, Problem A is related to the following result:

which implies that Siu’s lemma holds with C =1.

In [43], by developing the method established in [41] and using the iteration method established in [4] and [5], we obtained the following more general version of Siu’s lemma for psh weights with nontrivial multiplier ideal sheaves, which solves Problem A:

Moreover, any holomorphic extension F of f satisfying (4.3) has the property (4.4).

As an application of Theorem 4.1 and Theorem 2.5,we obtained in[43]the following refined optimal Lextension theorem with singular metrics in the K¨ahler case:

Theorem 4.2 Let R ∈ℜ, where ℜ is the same as in Theorem 3.1. Let Π : X -→S be a surjective proper holomorphic map from a K¨ahler manifold (X,ω) of dimension n to a Stein domain S contained in the unit ball B⊂C(1 ≤k ≤n), where ω is a K¨ahler metric on X. With respect to the coordinate functions on C, we regard Π as a k-dimensional vector of holomorphic functions s = (s,··· ,s) on X. Assume that 0 ∈S and ds := ds∧···∧dsis nonvanishing on

and assume that there exists a holomorphic extension Fof f to an open neighborhood of Xin X. Then there exists a positive number β and a holomorphic section F ∈H(X,mK+L)such that F =f on X,

Theorem 4.3 refines Theorem 3.3 by adding(4.8)and(4.10)to the conclusion and removing(3.2) from the assumption.

The improvement that Theorem 4.3 removes (3.2) from the assumption of Theorem 3.3 plays an important role in our proof of the next theorem on the positivity of twisted relative pluricanonical bundles with singular metrics in the K¨ahler case(see Section 6 in[43]);the reader is referred to [3, 5, 31] for the projective case, and to [7] for a related result in the K¨ahler case.

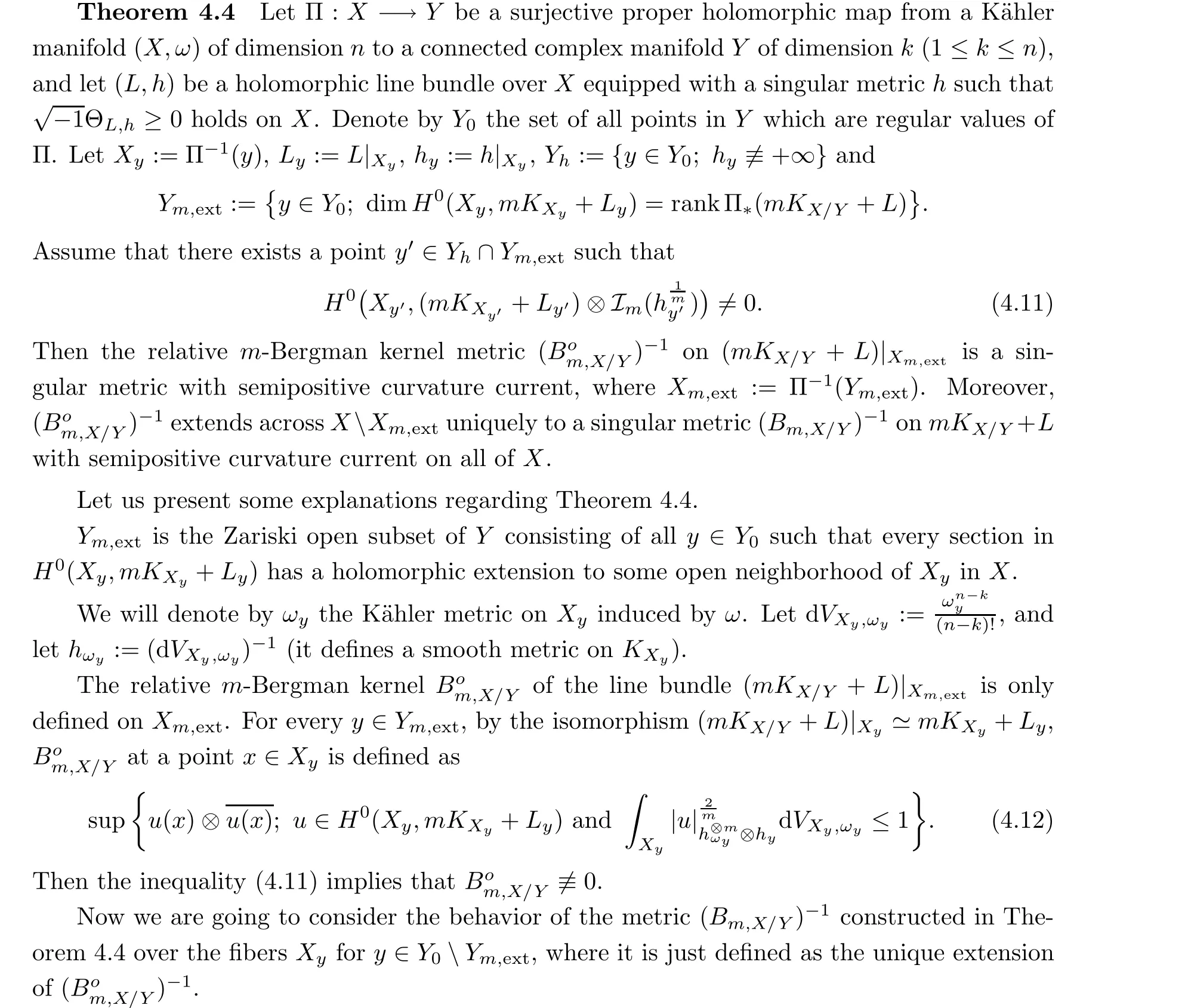
Another application of Theorem 4.2 and Theorem 4.4 is to prove the positivity of the direct images of twisted relative pluricanonical bundles with singular metrics for K¨ahler fibrations(see Section 8 and Section 9 in [43]). One can also see [3, 31] and [23] for the projective case.

Theorem 4.4 can also be used to study the subadditivity of Kodaira dimensions for K¨ahler fibrations. In [44], we introduced the notion of the generalized Kodaira dimensions with multiplier ideal sheaves, and proved the subadditivity of these generalized Kodaira dimensions for certain K¨ahler fibrations as an application of Theorem 4.4 and a general Lextension theorem with singular metrics on K¨ahler manifolds (see Theorem 2.8 and Remark 2.9 (b) in [14]). One can also see [35] for some related results.

5 Extension Theorems in the K¨ahler Case for Cohomology Classes with Values in Quotients of Multiplier Ideal Sheaves

If X is Stein, this problem is solved by Cartan’s Theorem B. For other cases, various advanced techniques have been developed.

In this section, φis required to be quasi-psh for a singular metric of a holomorphic line bundle when it is expressed locally as eon a local coordinate chart U (note that φis only required to be in Lfor a singular metric in other sections in this paper).

In [8], Cao, Demailly and Matsumura proved the following general extension theorem for cohomology classes on non-reduced analytic subspaces of holomorphically convex K¨ahler manifolds:

Theorem 5.1 Let X be a holomorphically convex complex n-dimensional manifold possessing a K¨ahler metric ω, let ψ be a quasi-psh function with neat analytic singularities on X,and let (L,h) be a holomorphic line bundle over X equipped with a singular metric h. Assume that α ＞0 is a positive continuous function on X, and that the following two inequalities hold on X in the sense of currents:

is surjective for every q ≥0.

Note that ψ is required in Theorem 5.1 to be a quasi-psh function with neat analytic singularities (see Section 2 for the definition). The general case when ψ is a quasi-psh function with arbitrary singularities was posed as a question in Remark 3.10 in [8].

In [45] (see also [39] for an announcement), we proved the following extension theorem for cohomology classes defined on a not necessarily reduced analytic subvariety of a holomorphically convex K¨ahler manifold, which gives an affirmative answer to the above question posed by Cao-Demailly-Matsumura:

A key point in our proof of Theorem 5.2 is that we introduce an idea to approximate two weight functions simultaneously (see Lemma 5.3 below). The constructive proof of Theorem

2.3 plays a key role in the proof of Lemma 5.3.

is injective for every q ≥0.

In the proof of Theorem 5.4,we take ψ =2 log|s|in Theorem 5.2. A key point is that ψ is neither required to have analytic singularities nor required to be quasi-psh in Theorem 5.2.

Theorem 5.2 was also used to obtain a vanishing theorem (see Theorem 2.2 in [45] for details).

For the above extension problem, it is desirable to obtain an optimal Lestimate. First,let us recall some notions and notations.

Let (X,ω) be an n-dimensional K¨ahler manifold, let ψ be a quasi-psh function on X, and let (L,h) be a holomorphic line bundle over X equipped with a singular metric h.

As in[14](Definition 2.11),the restricted multiplier ideal sheaf I(h)is defined to be the set of germs f ∈I(h)⊂Osuch that there exists a coordinate neighborhood U of x satisfying

is surjective.

In Theorem 5.6, we do not assume that ψ has analytic singularities. Theorem 5.6 was proved in [14] for an explicit function R with a non-optimal Lestimate in the case when ψ =(m-m)φ for a quasi-psh function φ on X with neat analytic singularities, where mare jumping numbers(see Theorem 2.13 in[14]for details,and see also[24]for a related result).

The integral in the inequality (5.2) depends on the property of h near {ψ = -∞} ⊃Y(see Definition 5.5), while the integral in the inequality (3.1) depends on the property of h on Y. In [44], we proved a limit property (Theorem 1.3 in [44]) for Lintegrals of holomorphic functions with psh weights near a subvariety, which is a more general version of Siu’s lemma for nontrivial multiplier ideal sheaves near a subvariety. This limit property gives a relation between (5.2) and (3.1), and then gives a relation between Theorem 3.1 (or the more general version in [42]) and Theorem 5.6 (see Section 7 in [44]).