Derived sequences and the factor spectrum of the period-doubling sequence

we define ω[i,j]=ω[i;j-i+1]=xx···xx. By convention,ω[i]=ω[i,i]=ω[i;1]=xand ω[i,i-1]=ω[i;0]=ε(the empty word). We call ω[i,j]a factor of ω,denoted by ω[i,j]≺ω.The position of factor ω[i,j] in ω is defined to be i. Let ρ be a recurrent sequence and let P be a property. Then, a fundamental problem is finding out all factors ω in the sequence ρ and positions n ∈N such that the occurrence of ω starting at position n fulfills the property P. For solving this problem, we have introduced the factor spectrum [16], as follows:

Definition 1.1 Letting ρ be a recurrent sequence and letting P be a property,the factor spectrum related to ρ and P is defined as

where Ωis the set of all factors in ρ.

Notice that there is a slight difference from the definition of the factor spectrum given in Huang-Wen [16]. The definition here is more convenient for broad application.

For a given sequence ρ and a property P, determining the factor spectrum is a difficult problem in general. We need not only find all positions of each factor ω ∈Ωin the sequence ρ, but we should know if the occurrence of ω starting at position n satisfies the property P. Wen-Wen [23] considered some special factors of the Fibonacci sequence, called singular words,and discussed the recurrent structure and derived sequence for each singular word,then established a decomposition by the singular words. By these results, we can determine the factors having given properties,but we do not discuss the corresponding factor spectrum. For a general primitive substitution, Durand[5] introduced return words and a derived sequence,but that is not enough to determine the factor spectrum, since we need to know the structures and properties of the return words and derived sequences. Based on the singular words,Huang-Wen[13]considered general factors of the Fibonacci sequence and introduced the notion of the kernel word,which plays an essential role in these studies. By developing some new ideas and related techniques, some typical factor spectra were determined, and some interesting applications obtained [12, 15, 17]. Huang-Wen generalized the results to the Tribonacci sequence [14]; for some other cases, see [12, 17].

1.1 Example 1: about two variables of the factor spectrum

This example shows that, given a property P and a factor ω,at some position, ω fulfils the property P, and for some other positions, ω does not fulfil the property P. Thus, whether a factor fulfils a property depends on its position.

Let A = {a,b} be a binary alphabet. The period-doubling sequence D is the fixed point of the substitution σ(a) = ab and σ(b) = aa beginning with the letter a, which is a recurrent sequence. Let Pbe a property called a“square”such that(ω,n)∈Spt(P)means D[n;2|ω|]=ωω. Take ω = ab for instance. It is easy to check that ωω = abab is a square in D. However,not all occurrences of ab in D satisfy property P. Using factor spectrum, we can distinguish the occurrences of the same factor in different positions:

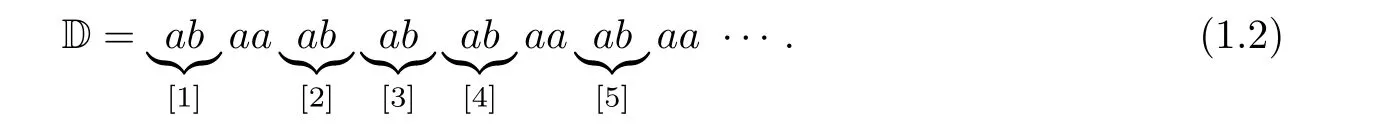
We let notations [1] to [5] denote the first five occurrences of ω in Equation (1.2). Thus the

1.2 Example 2: visualization of the factor spectrum

In Figure 1(a), we visualize the factor spectra for factor ω = ab and properties P(i =1,2,3), which are colored grey, orange and red, respectively. For instance, the grey cell in line 1 column 1 means that a factor ω = ab occurs at position n = 1. Moreover, the cell in line 2 column 1 is white; this means the factor ω = ab that occurs at position n = 1 is not followed by another ω =ab, i.e., square ωω =abab does not exist at this position. Notice that,if (ω,n) ∈Spt(P), then (ω,n) ∈Spt(P) for i = 2,3. Thus we can put the three lines in Figure 1(a) in just one line. Therefore we obtain a more simple visualization of the factor spectra; see Figure 1(b).

Figure 1 (Color online) The factor spectra for a fixed factor and several progressive properties

The above analysis is about a fixed factor and several progressive properties. We can also study the factor spectrum for a fixed property and several factors. In Figure 2, we consider several prefixes of D and property P. Obviously,there exist some relations among the positions n where they occur. In particular, the set {n | (ω,n) ∈Spt(P),ω = abaaaba[1,h]} is the same for 4 ≤h ≤7.

Figure 2 The factor spectrum for property P1 and several prefixes of D

1.3 Organization of the paper

In this paper, we will study the factor spectrum of the period-doubling sequence; this is a typical sequence generated by 2-automatons and appears often in number theory,mathematical physics and dynamical systems. For this sequence, the methods mentioned in Wen-Wen [23]and Huang-Wen [13, 14] are not valid. In Sections 2 to 6, some new ideas, containing new terms such as envelope word and envelope of a factor,and techniques will be introduced. These can be used to give the structure and some important properties of return words and derived sequences of the period-doubling sequence D. Then we will find the local structure near each occurrence of ω in D. In Section 7, using the results obtained, we determine the factor spectra in D for some typical properties. Section 8 is devoted to establishing the reflexivity property of derived sequences which characterise the structure of the derived sequences.

2 The Return Word and Derived Sequence of D

Wen-Wen [23] and Huang-Wen [13, 14] proved that for any factor, a derived sequence of the Fibonacci sequence (resp. the Tribonacci sequence) over any factor ω is still the Fibonacci sequence (resp. the Tribonacci sequence) itself. Using these properties, we determined the numbers of palindromes, squares and cubes occurring in each factor of F and T; see [15] for more details. These topics are of great importance in computer science.

For the period-doubling sequence D though, there are two difficulties. First, the main tool of [13, 14] is the kernel word. However, in the study of the period-doubling sequence D, the technique of kernel words fails. In fact, there is no well-defined kernel set in D. To overcome this difficulty, we introduce two new notions: the envelope word and the envelope of a factor(see Equations (3.3) and (3.4)). Second, the derived sequences of D over two distinct factors may be different (see examples in Equations (3.1) and (3.2)). Fortunately, we can divide set Ωinto two types, each type corresponding to one derived sequence.

2.1 The return word and derived sequence

We call a non-empty word ν a prefix(resp. suffix)of a word ω if there exists a word u such that ω = νu (resp. ω = uν), which is denoted by ν ◁ω (resp. ν ▷ω). In this case, we write νω = u (resp. ων= u), where νis the inverse word of ν such that νν= νν = ε.A palindrome is a finite word that reads the same backwards as forwards. Let ρ be a recurrent sequence,and let ω and W be two factors of ρ. We let ωdenote the p-th occurrence of ω,and we let(ω)denote the position of ω. We note that ω=Wif ω =W and(ω)=(W). Moreover,we note that ω≺Wif ω ≺W and that (W)≤(ω)＜(ω)+|ω|-1 ≤(W)+|W|-1.

The definitions of both the return word and the derived sequence are from Durand [5].We recall them below. Notice that Durand gave these notions for all prefixes of any recurrent sequence (but we find these notions are fit for all non-empty factors).

Let ρ be a recurrent sequence and let ω be a non-empty factor of ρ. We call ρ[(ω),(ω)-1] the p-th return word over ω, denoted by R(ω). Denote by Hthe set of return words over factor ω ≺ρ. Then the sequence ρ can be written in a unique way as a concatenation ρ=ρ[1,(ω)-1]R(ω)R(ω)···,where R(ω)∈H. By convention,we denote R(ω)=ρ[1,(ω)-1], which is not a return word. Let us give to Hthe linear order defined by the rank of the first occurrence in ρ. This defines a one to one and onto map Λ: H→{1,...,Card(H)}=:N, and the sequence

This sequence of alphabet Nis called a derived sequence of ρ. Notice that we omit the prefix ρ[1,(ω)-1]. Moreover, we let Θ:N→Hdenote the reciprocal map of Λ.

The main result of Durand [5] is that a sequence ρ is substitutive primitive if and only if the number of its different derived sequences is finite. The other property is that for any ω ≺ρ and v ≺D(ρ), there exists a factor μ ≺ρ such that derived sequence is D(D(ρ)) = D(ρ);see Proposition 6(5) in [5]. By the two properties, for any ω ≺ρ, the derived sequence D(ρ)is still substitutive primitive.

2.2 The period-doubling sequence

Let A={a,b}be a binary alphabet. We define·:A →A by a=b and b=a. The perioddoubling sequence D has been heavily studied in mathematics and computer science. Damanik[7] determined the numbers of palindromes, squares and cubes of length n occurring in D.Allouche-Peyri`ere-Wen-Wen[2] proved that all the Hankel determinants of D are odd integers.We also refer readers to [1, 4, 6, 8-11, 18, 22]. We denote A= σ(a) and B= σ(b)for m ≥0. Then |A| = |B| = 2. Let δ∈{a,b} be the last letter of A. Obviously,δ=a if and only if m is even,and δis the last letter of B. Moreover Aδ=Bδ.Let Rand Rbe two words over the alphabet A. The period-doubling sequence over the alphabet{R,R} is denoted by D(R,R). The sequence D can be written in a unique way as a concatenation D = R(ω)R(ω)R(ω)···. The sequence D(D) = {Λ(R(ω))}is the derived sequence over factor ω.

3 Research Ideas, Definitions and Main Results

As mentioned earlier, derived sequences of D over two distinct factors may be different.Take factors b and aa for instance. By the definition of a return word, R(b) = baaa and R(b) = ba. Furthermore, we denote Λ(R(b)) = α and Λ(R(b)) = β. Then the derived sequence over factor b is D(D)=D(α,ββ); see Equation (3.1).

Obviously, The derived sequences D(D) and D(D) are different. In order to accurately describe the derived sequence D(D) for any factor ω,we give two types of special factors in D,called the envelope words (see Definition 3.1). These satisfy the following properties: (1) The derived sequence over any envelope word of type 1 is D(α,ββ)and the derived sequence over any envelope word of type 2 is D(αβ,αγαγ) (see Theorem 3.2); (2) There exists a unique envelope for each factor, denoted by Env(ω), and the difference (ω)-(Env(ω))=(ω)-(Env(ω))is independent of p (see Theorem 3.5).

Table 1 The first few letters of D, D(α,ββ) and D(αβ,αγαγ)

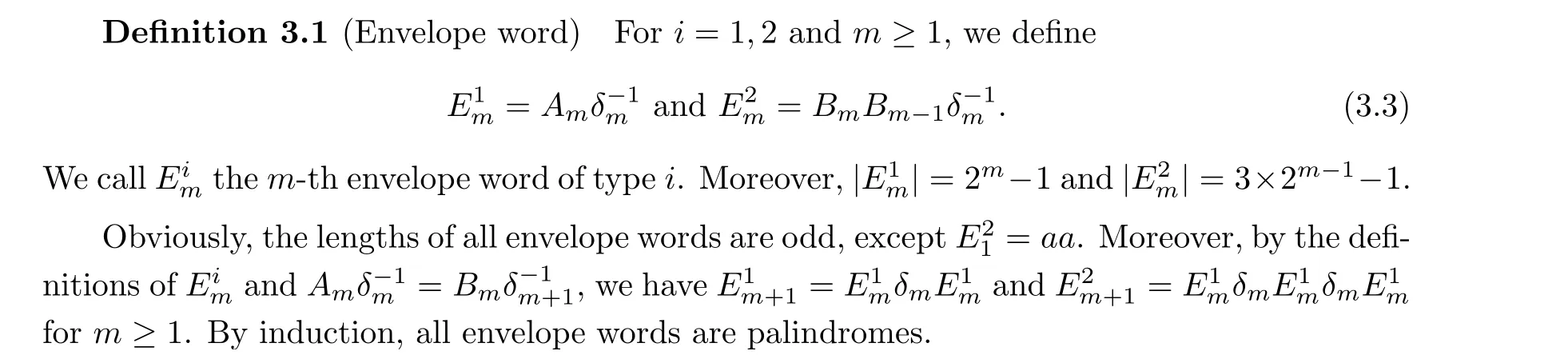
Table 2 The first few values of Am, Bm, E1m and E2m

Theorem 3.2 (Derived sequence over envelope word) For any m ≥1, we have the derived sequence D(D)=D(α,ββ) and the derived sequence D(D)=D(αβ,αγαγ).

where 0 ≤j ≤|Env(ω)|-|ω|, |u| =j, u ◁Env(ω) and ν ▷Env(ω). In fact, j is unique for any fixed ω, i.e., each factor ω in D occurs exactly once in Env(ω) (see Lemma 5.3).

Figure 3 The relation between Env(ωp) and Env(ω)p, where ω =baa and Env(ω)=E13 =abaaaba

Theorem 3.5 (The relation between Env(ω) and Env(ω))

For all (ω,p)∈Ω×N, Env(ω)=Env(ω).

Theorem 3.5 plays an important role in our studies. Using Theorem 3.5, we can extend derived sequences of D from envelope words (Theorem 3.2) to general factors (Theorem 3.6).The proof of Theorem 3.5 will be given in Section 5.

Theorem 3.6 (Derived sequence over any factor) For any factor ω ≺D, we have that:(1) if there exists an integer m ≥1 such that Env(ω) = E, we get the derived sequence D(D) = D(α,ββ); (2) if there exists an integer m ≥1 such that Env(ω) = E, we get the derived sequence D(D)=D(αβ,αγαγ).

The proofs of Theorem 3.6 will be given in Section 6,as well as the more accurate expressions of R(ω) for ω ≺D and p ≥1. As an application of Theorem 3.6, we give the positions of all occurrences of ω in D.

The other two results in this paper are as follows:

(1) Using the structures of derived sequences, we determine the factor spectra for some combinatorial properties (see Section 7).

(2) For any ω ≺D and v ≺D(D), the derived sequence D(D(D)) is still D(α,ββ) or D(αβ,αγαγ). We call this the reflexivity property of a derived sequence (see Section 8).

4 Proof of Theorem 3.2

Our goal in this section is to prove a more accurate form of Theorem 3.2 as below, which determines the derived sequences for all envelope words. We can see Equation (3.2) as an example.

Let ω be a factor of a sequence ρ. How do we determine all occurrences of ω in ρ? An immediate method is to check whether or not ρ[i,i+|ω|-1]is equal to ω for all i ≥1. Letting u be a proper factor of ω, we have that 0 ＜|u| ＜|ω|, and there exist two words μ and ν subject to ω = μuν. If we already know all positions of u in ρ, we can discover all ω by a simpler method, called the factor extending method. This method works due to the fact that if ω occurs at position L, then u occurs at position L+|μ|; i.e.,

Thus an occurrence of u can extend to ω if and only if this u is preceded by the word μ and followed by the word ν. In this case, we say the factor u at this position can extend to a ω.

Lemma 4.1 Aoccurs exactly twice in both AAand ABAfor m ≥0.

Proof The result is clearly true for m = 0. Assume that the result is true for m. Then all positions of Ain AAand ABAare shown with underbrace, as below.

Among these, only the Aat positions [1], [2], [3] and [6] are followed by B. By the factor extending method, A= ABoccurs twice in both AAand ABA.Thus the conclusion holds for m ≥0, by induction.□

(2) The proof can be obtained by an analogous argument.□

5 Proof of Theorem 3.5

Theorem 3.5 is equivalent to stating that the difference

is independent of p, where integer j is given in Equation (3.5).

By Equation(3.5),for all p ≥1,there exists an integer q ≥p such that(ω)-(Env(ω))=j.In fact, if a word Env(ω) occurs at position L, a word ω occurs at position L+j. In order to prove Theorem 3.5, i.e., q =p, we only need to prove Proposition 5.1, below.

Proposition 5.1 Every occurrence of ω in the period-doubling sequence is preceded by word u and followed by word ν, where the words u and ν are given in Equation (3.5). This means that every occurrence of ω can extend to a Env(ω).

We first list all factors with envelope E(m = 1,2). We can check them one by one to prove Proposition 5.1 for m=1,2.

In order to prove Proposition 5.1 for m ≥3, we first give two lemmas.

Lemma 5.2 Let ω be a factor of D. (1) If there exists an integer m ≥3 such that Env(ω)=E, then ω must contain at least one element in set

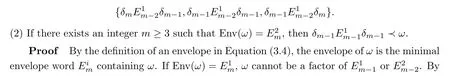
Figure 4 Fine structures of E1m and E2m for m ≥3

This completes the proof.□

Lemma 5.3 Each factor ω in the period-doubling sequence D occurs exactly once in Env(ω). Thus, for each factor ω, there exists one and only one integer j such that ω =Env(ω)[j+1,j+|ω|].

Proof This conclusion can be checked easily for m = 1,2. For m ≥3, we first consider the case that Env(ω) = E. By Lemma 4.1, all positions of Ain Eare shown with underbrace, as below.

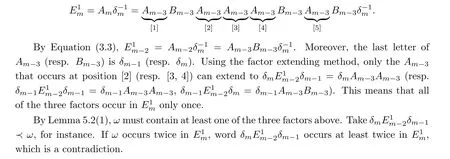
The proofs of other cases can be obtained by analogous arguments.□

By Lemmas 5.2 and 5.3 above, in order to prove Proposition 5.1 for m ≥3, we only need to prove Proposition 5.4 for m ≥3, as below.

(2) The proof can be obtained by an analogous argument.□

6 Proof of Theorem 3.6

In this section, we let W denote Env(ω), for short. For all p ≥1,the p-th return word of ω(resp. Env(ω)=W) is R(ω)=D[(ω),(ω)-1] (resp. R(W)=D[(W),(W)-1]).Let ω ≺D have the expression in Equation (3.5), i.e., ω =W[j+1,j+|ω|] and W =u·ω·ν,where 0 ≤j ≤|W|-|ω| and |u|=j. By Figure 5, |R(W)|＞|u|=j. Thus u ◁R(W) for all p ≥1.

Figure 5 If |RD,p(W)|≤|u| for some p ≥1, both ωp and ωp+1 occur in Wp+1,contradicting Lemma 5.3

By Theorem 3.5, (ω)-(W)=j for all p ≥1. Thus

An immediate corollary of Equation (6.1) is (ω)-(ω)= |R(ω)| = |R(W)| for p ≥1 (see Figure 6 for instance, where j =1 and u=a).

Figure 6 The first few return words of ω =baa and W =Env(ω)=abaaaba

Since u is only dependent on ω, R(ω) = R(ω) if and only if R(W) = R(W)for any p /= q. By the definitions of a derived sequence and map Λgiven in Section 1,D(D)=D(D).

Thus we extend Theorem 3.2 to Theorem 3.6.□where D(α,ββ)[1,p-1]is the prefix of sequence D(α,ββ)with length p-1,and|D(α,ββ)[1,p-1]|is the number of letter α occurring in D(α,ββ)[1,p-1]. The second equality holds by Theorem 3.6’. The third equality holds by |D(α,ββ)[1,p-1]|+|D(α,ββ)[1,p-1]|=p-1.(2) By an analogous argument, we obtain the conclusion for Env(ω)=E.□Taking ω =b and Env(b)=E, for instance, {(b)|p ≥1}={2,6,8,10,14,18,22,24,...},by Proposition 6.1. We can check this conclusion by Equation (3.1).

7 The Factor Spectra of D

Obviously, property Pis the same as P(called a “square”) defined in Section 1.

In Section 7.1, we first find out all ωsatisfying these properties using the structure of derived sequences(Theorem 3.6’). Thus we can refine some classical conclusions. In Section 7.2,using the positions of all occurrences of ω (Proposition 6.1), we give the factor spectra of properties P(i=1,2,3) for all factors with length 2for m ≥0.

7.1 Three combinatorics properties

Figure 7 Several subsets of (ΩD,N)

Theorem 7.1 (1) ω∈Pif and only if (ω,p)∈S∪S∪S;

(2) ω∈Pif and only if (ω,p)∈S; (3) ω∈Pif and only if (ω,p)∈S∪S.

Similarly, we can obtain the conclusion in other cases.□

7.2 The factor spectra

Using the factor spectra of properties P(occurrence), P(square), P(cube), we can refine these classical conclusions. In Figure 8,we visualize the factor spectra for all factors with lengths 2(m=0,1,2) and properties P(i=1,2,3), these are colored grey, orange and red,respectively.

Figure 8 (Color online) The factor spectra for all factors with lengths 2m (m=0,1,2) and properties Pi (i=1,2,3)

7.3 Further research

So far, we have found the factor spectrum by the structure of derived sequences. The process is quite complicated. Notice that the visualization of the factor spectrum has some fractal properties,in particular,has some self-similar structure. We wish,in future research,to find out a finite generation rule of the factor spectrum, and to treat more general sequences by more general methods.

8 The Reflexivity of Derived Sequences

Define three alphabets A = {a,b}, B = {α,β} and C = {α,β,γ}. Define map τ: A →B by τ(a) = α and τ(b) = ββ. Define map τ: A →C by τ(a) = αβ and τ(b) = αγαγ.Obviously, τ(D)=D(α,ββ) and τ(D)=D(αβ,αγαγ). Thus we can rewrite Theorem 3.6.

Theorem 3.6” For ω ≺D and Env(ω)=E(k =1,2),the derived sequence is D(D)=τ(D).

Table 3 The first few values of kEim for k,i=1,2

We omit the proof, which is quite simple but tedious in terms of notation. More accurate expressions are given in Proposition 8.3. For ease of understanding, we show the reflexivity relations among D, τ(D) and τ(D) in Figure 9, and give four examples in Figure 10.

Figure 9 The reflexivity of derived sequences. For instance, the edge“Dτ1(D)=D(α,ββ)” means that for any ω ≺D, if Env(ω)=E1m,then the derived sequence is Dω(D)=τ1(D)=D(α,ββ)

Figure 10 Four examples of derived sequences in τ1(D) and τ2(D)