基于同位模式的北京城市职住要素研究
2021-02-22陈思宇孟斌李梦天
陈思宇 孟斌 李梦天

[摘要]空间同位模式是指在一定空间范围内频繁发生并且位置相邻的事件集合,对于研究不同空间要素之间交互关系具有重要意义。城市中职住要素的研究是很典型的同位模式。基于Ripley′s K函数基础上变形的双变量K(r)函数和双变量g(r)函数,对获取到的北京市五环内职住要素和交通要素进行空间同位模式分析,最终得出:1)住宅区和写字楼之间的同位模式较为复杂,低价位住宅区与写字楼之间不存在同位模式;中等价位住宅区和高价
位住宅区与写字楼存在同位模式,但尺度范围不同;2)不同价位住
宅区与地铁站之间都在0~2 km范圍上具有空间同位模式,并且随着距离的增加,住宅区与地铁站的空间同位模式强度在不断减弱;3)写字楼与地铁站点同样在中距离范围内具有空间同位模式,并且随着距离的增加,空间同位模式的强度均在减小。
[关键词]空间同位模式;Ripley′s K函数;职住关系
[中图分类号]TU 984[文献标志码]A[文章编号]10050310(2021)01002009
Research on the Elements of Beijing′s Urban JobsHousing
Based on the Colocation Model
Chen Siyu, Meng Bin,Li Mengtian
(College of Applied Arts and Science, Beijing Union University, Beijing 100191, China)
Abstract: Spatial colocation mode refers to a collection of events that frequently occur within a certain spatial range and are located adjacent to each other, which is of great significance to the study of the interaction between different spatial elements. The research on the elements of the urban jobshousing is a typical colocation model. Based on the deformed bivariate K(r) function and bivariate g(r) stemming from Ripley′s K function, this paper analyzes the spatial colocation pattern of the acquired elements of jobshousing and traffic within the Fifth Ring Road of Beijing, and finally obtains: 1) The colocation pattern between residential buildings and office buildings is complicated. There is no colocation pattern between lowpriced residential areas and office buildings; mediumpriced residential areas and highpriced residential areas have colocation patterns relationship with office buildings, but the scale ranges are different. 2) There is a spatial colocation pattern between residential buildings of different prices and subway stations in the range of 0~2 km. As the distance increases, the intensity of the spatial colocation pattern between residential buildings and subway stations constantly weakens. 3) Office buildings and subway stations also have spatial colocation patterns in the middledistance range. As the distance increases, the intensity of the spatial colocation patterns decreases.
Keywords: Colocation pattern; Ripley′s Kfunction; Relationship of jobshousing
引言
空间同位模式是指频繁地出现在同一区域的一组空间要素或事件[12]。例如,生态学中的尼罗鳄与埃及燕鸻、经济学中的供应商与制造商的分布,均是典型的同位模式[3]。空间同位模式的挖掘是空间关联性挖掘的一种,逐渐成为空间挖掘中的一项重要任务[45],有助于揭示地理现象或事件的分布规律。空间同位模式挖掘的方法主要可分为空间统计方法和数据挖掘方法两类[6],其中,空间统计方法是通过关联性指标去描述不同类空间要素之间的关系,这些指标包括交叉K函数、平均最近邻距离、空间回归模型、同位系数、Q 统计等[712]。
居住和就业是城市活动的两大基本功能,城市居住与就业分布及关系的研究对城市的规划和管理有极大的影响[13]。由于改革开放以来我国经历了快速的城市化,城市居民职住分离现象日趋严峻,职住过度分离对城市个体和整体都会产生严重影响[14]。城市职住空间是城市空间结构与形态特征的重要方面,也是影响城市功能正常运行与居民生活质量的重要内容[15]。在职住关系研究中,以距离或通勤时间的研究成果较多,但对居住地和就业地及交通节点等职住要素的布局模式关注相对较少,张景秋等对北京写字楼的空间集聚模式进行了系统研究,得出各行业总体呈“大分散,小聚集”“大分散、大聚集”和“小分散、大聚集”3种分布模式[16];牛方曲等对住宅的空间布局进行了分析,在综合考虑
政策限制和市场规律模拟开发商决策行为后,构建了FDM模型,为城市空间模拟分析提供了良好的解决方案[17]。研究居住地与工作地两种要素在空间上是否同位,能够有效揭示城市职住要素的分布规律,极大地优化城市职住空间结构,保障城市功能正常运行。利用空间模式研究中的同位模式,可以定量研究城市职住要素的同位模式,推进城市职住要素的研究。
在特大型城市中,考虑到城市功能分区,居住和就业分区布局成为一种常态,一般通过交通节点将居住要素和就业要素进行连接。本文基于空间同位模式,利用Ripley′s K函數对北京市五环内的住宅区、写字楼以及地铁站点进行分析,为促进城市职住平衡、合理配置城市要素提供理论和实证支持。
1研究区概况与数据来源
1.1研究区概况
北京市五环内区域是北京城市的中心区域,包括东城区、西城区的全部以及朝阳区、海淀区、石景山区、丰台区的大部分区域。根据国家统计局在2015年发布的北京环路人口分布数据显示,北京市五环内有1 054万常住人口,占全市人口的48.9%。北京市五环内有CBD、金融街、中关村、三元桥、望京、总部基地、亚运村等就业集聚区,根据《2018年北京区域统计年鉴》,仅东城区、西城区、朝阳区和海淀区的生产总值就为17 746亿元,占北京市当年生产总值的63.3%。北京市五环内常住人口众多、地铁网络密集、经济发达、职住问题突出,是研究职住关系的重点区域,因此,本文将研究区选择为北京市五环内区域。
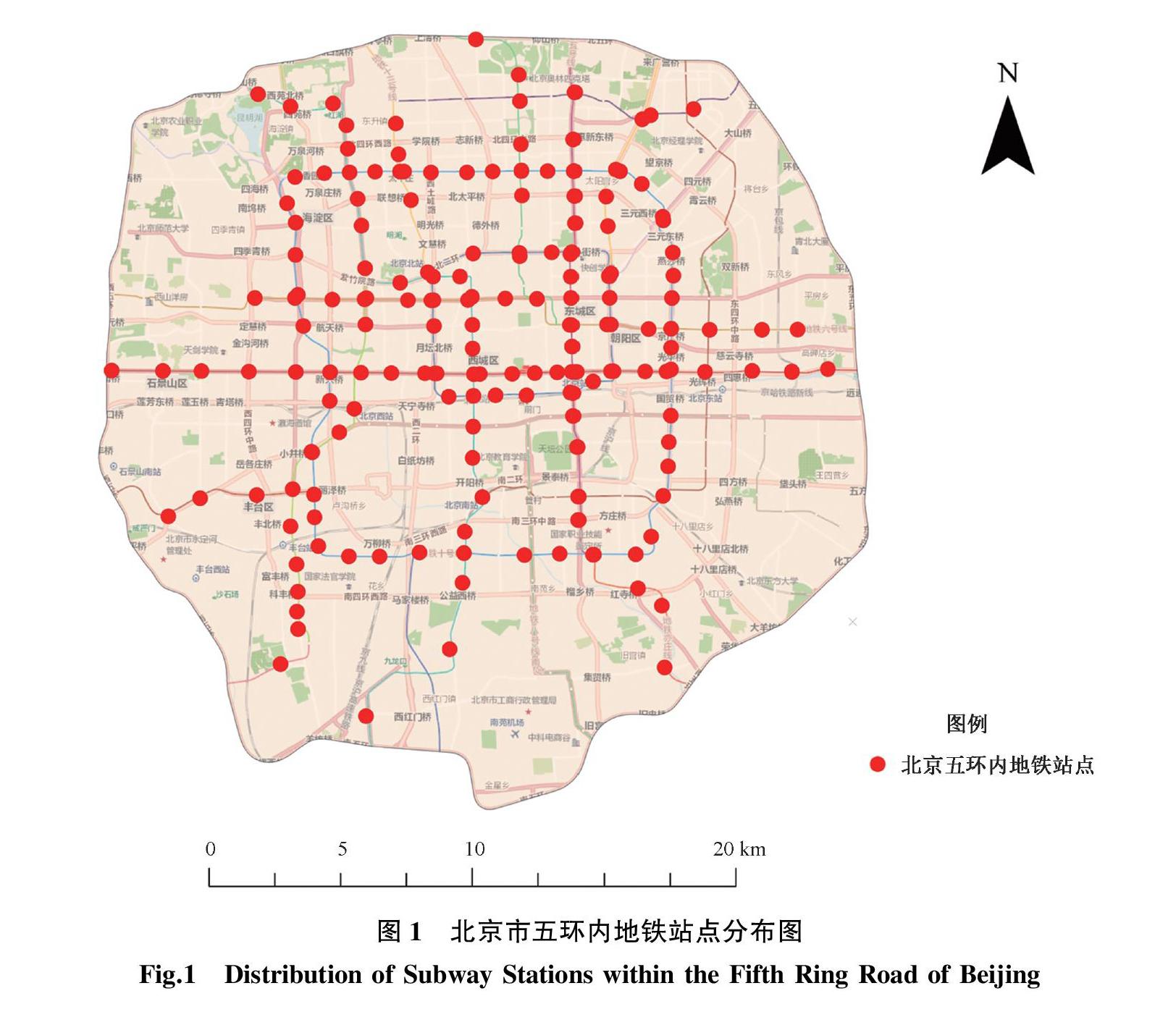
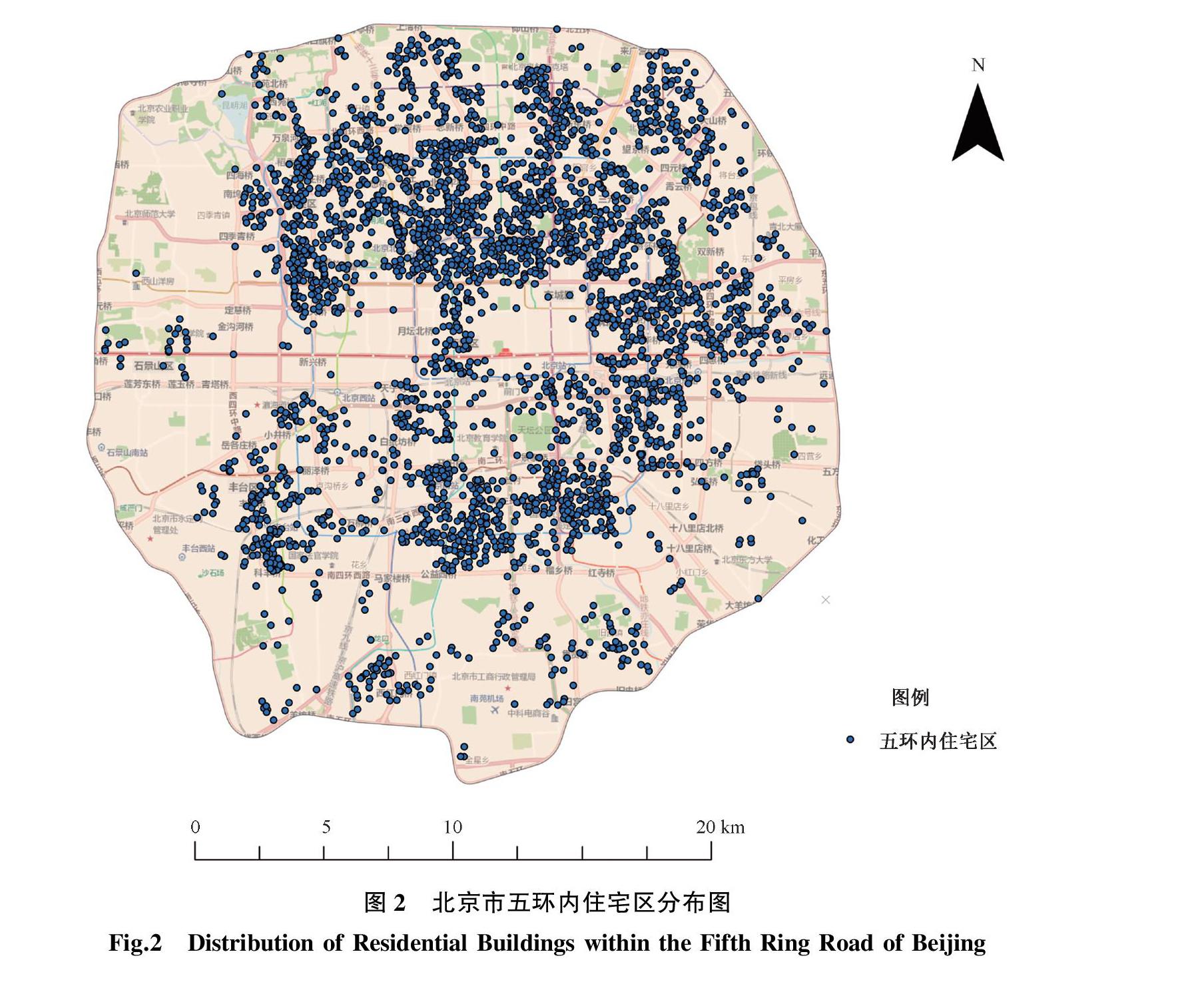
本论文以北京市五环内的写字楼、住宅区、地铁站点为研究对象,其中,通过对北京市租房网站使用八爪鱼软件抓取2016年带有经纬度坐标信息的写字楼数据和住宅区数据,并结合2016年北京市五环内地铁站点数据进行分析,共获得北京市五环内住宅区数据4 905条,写字楼数据3 171条,地铁站点数据186条(见图1、图2、图3)。
由于对于住宅区中高低价位标准有不同划分,本文采用均价正负一个标准差的方式将住宅区数据分为高价位住宅区、中等价位住宅区及低价位住宅区3类,其中,高价位住宅区价格≥59 614元/平方米,共544条数据;中等价位住宅区价格为27 816元/平方米~59 613元/平方米,共3 938条数据;低价位住宅区价格≤27 815元/平方米,共423条数据。
本文采用R 3.5.3软件对获得的数据进行分析和统计。本文中Ripley′s K(r)函数、g(r)函数、双变量K(r)函数、双变量g(r)函数皆采用R软件中的ads软件包进行分析。
2研究方法
对实际的地理对象点集进行集聚模式分析时,仅仅使用最邻近距离会掩盖结果中的其他模式[12],为了解决这一问题,Ripley对事件之间的所有距离进行研究,提出了K函数方法。与其他单一距离分析工具不同,Ripley′s K函数最大的优势在于可以研究不同尺度上的空间分布模式。本文使用基于Ripley′s K 函数变形的双变量K(r)函数和双变量g(r)函数进行研究。
2.1双变量K(r)函数分析法
Ripley′s K(r)用于分析不同空间尺度上的聚集程度是否一致,发现是否存在聚集及聚集的空间尺度。公式为
Kr=An2ni=1nj=1IrUijWiji≠j。(1)
式中,当要素i与要素j之间的距离Uij≤r时,Ir为1,否则为0。Wij为权重,是以i为圆心
、Uij为半径的圆周长在样地面积A中的比例;A为面积,n为面积内要素的总数;r为空间尺度。
因为Ripley′s K(r)函数只适用于研究一类要素随距离变化所呈现出的空间模式,所以Diggle在此基础上进行了改进并提出双变量K函数[18],使改进后的双变量K函数能对两类要素进行分析。其公式为
K12r=An1n2n1i=1n2j=1IrUijWiji≠j。(2)
式中,n1和n2分别代表样地面积内两类要素的总个数;i和j分别代表第一类要素和第二类要素,而
A、Ir(Uij)、Wij的含义与公式(1)相同。
使用蒙特卡罗(Monte—Carlo)拟合检验,计算上下包迹线,即置信区间。当实际的要素分布数据计算得到的K12(r)值高于置信区间时,则代表要素1与要素2之间在此尺度下具有空间同位模式。
2.2双变量 g(r)函数分析法
Ripley′s K(r)函数及双变量K函数在多尺度空间分布格局和空间关联性的研究中有着广泛的应用,但其也存在着一些不足之处:Ripley′s K(r)函数是计算以指定距离为半径的圆中的所用信息,但随着距离的不断增加,大尺度上的计算结果包含了小尺度的信息,这种累积效应使大尺度上的效应与小尺度上的效应相混淆。
g(r)函数通过对Ripley′s K(r)函数的改进,从而避免了以上问题。g(r)函数与Ripley′s K(r)函数最大的不同在于,Ripley′s K(r)函数是计算以r为半径的圆内的要素,而g(r)函数计算以r为半径,dw为面积的圆环内的要素(图4和图5)。g(r)函数能有效地消除大尺度格局在分析时容易受小尺度上信息影响的缺点,是与Ripley′s K(r)函数成对使用的重要函数。同理,双变量g(r)函数公式为
g12r=
dK12(r)2πdr。(3)
与K(r)函数相同,采用蒙特卡罗(Monte—Carlo)模拟检验计算置信区间,以检验两类要素之间是否具有显著性。若实际的要素分布数据计算得到的g12(r)值高于置信区间,则代表要素1与要素2之间具有空间同位模式。
3结果与分析
3.1住宅区与写字楼空间同位模式分析
基于双变量K、g函数计算结果得到,低价位、中等价位和高价位住宅区与写字楼在不同尺度下的同位模式不同:低价位住宅区与写字楼之间不存在同位模式;中等价位住宅区与写字楼在0~2 km范围内有同位模式;高价位住宅区与写字楼在4.8~6.3 km范围内有同位模式。
K、g函数图,其中,纵坐标是数据归一化后的表达;横坐标则是构建的圆的边界到住宅区的距离。
如图6(a)、6(c)、6(e)所示,观察不同价位住宅区与写字楼的K(r)函数发现,虽然3种价位住宅区与写字楼的实际值在一定距离内与高置信值相距较近,并且实际值都有上升趋势,但总体来看都没有超过置信区间,因此都不具有同位模式;如图6(b)、6(d)、6(f)所示,观察不同价位住宅区与写字楼的g(r)函数发现,中等价位住宅区与写字楼在0~2 km范围内的实际值高于置信区间;高价位住宅区与写字楼的实际值在4.8~6.3 km范围内高于高置信值,即中高价位住宅区与写字楼在不同距离范围内具有空间同位模式。
3.2不同价位住宅区与地铁站点空间同位模式分析
基于双变量K、g函数计算结果得到,低价位、中等价位和高价位住宅区与地铁站点在不同距离范围下的同位模式不同:不同价位住宅区与地铁站之间都在0~2 km范围上具有空间同位模式,并且随着距离的增加,不同价位住宅区与地铁站的空间同位模式强度在不断减少。
如图7(a)、7(c)、7(e)所示,观察不同价位住宅区与地铁站的K(r)函数发现,低价位住宅区与地铁站的实际值完全位于置信区间内,因此不具有空间同位模式;中高
价位住宅区都无限趋近于高置信值,但并不能说明其具有空间同位模式。同样,
如图7(b)、7(d)、7(f)所示,观察不同价位住宅区与地铁站的g(r)函数发现,不同价位住宅区与地铁站都会在小于2 km的某些距离范围上的实际值高于高置信值,即在这些范围内具有同位模式。
3.3职住要素与地铁站空间同位模式分析
基于双变量K、g函数计算结果得到,住宅区与地铁站和写字楼与地铁站都在中距离范围内具有空间同位模式,随着距离的增加,空间同位模式的强度在减小。同时,写字楼与地铁站空间同位模式的强度要大于住宅区与地铁站。
如图8(a)、8(c)所示,观察住宅区与地铁站和写字楼与地铁站的K(r)函数发现,住宅区与地铁站和写字楼与地铁站的实际值都只是接近于高置信值,但是并没有超过,即住宅区与地铁站和写字楼与地铁站均不具有同位模式。
如图8(b)、8(d)所示,观察住宅区与地铁站和写字楼与地铁站的g(r)函数发现,住宅区与地铁站和写字楼与地铁站的实际值都存在高于高置信值的现象,即具有空间同位模式。但是,对比住宅区与地铁站和写字楼与地铁站的数据发现,两者之间集聚的程度有较大的区别。写字楼与地铁站比住宅区与地铁站在更短的距离上有空间同位模式,并且写字楼与地铁站存在同位模式的距离比住宅区与地铁站远且持续,住宅区与地铁站虽在0~4 km范围内具有空间同位模式,但也只是零星存在。
4结论与讨论
4.1方法评述
通过对以上结果分析,可以发现K(r)函数与g(r)函数在进行空间同位模式分析时结果差异明显,这主要是由于方法本身的计算所导致的。K(r)函数与g(r)函数的最大不同之处在于,K(r)函数是用半径不断增加的圆去计算不同空间尺度下的格局,具有一定的累积效应,这使得在不同距离内的信息会相互干扰。g(r)函数则是计算给定距离周围所构成的圆环内的密度比例,对其进行空间同位模式分析,所以g(r)函数在3 km范围内反映格局的变化,而在10 km范围内波动较少。总之,使用K(r)函数去描述要素的空间格局全貌会较快捷,且较能反映其整体特征,但K(r)函数忽略了空间格局及其关联性细节的变化特征。所以,若要研究要素空间格局与生态过程有联系的“关键尺度”,即空间格局的局部变化特征时,g(r)函数分析得到的结果将更加接近实际情况[22]。在研究空间格局及空间同位模式时,结合K(r)函数与g(r)函数各自的长处,能够更充分地探索空间格局。
4.2结论与建议
本文运用在Ripley′s K(r)函数的基础上进行改进和提升的双变量K(r)函数、双变量g(r)函数,对北京市五环内的职住要素和地铁站点数据进行空间同位模式分析,最终得出:
1) 职住要素空间同位模式分析的结果表明:低价位、中等价位和高价位住宅区与写字楼在不同距离范围内的同位模式不同,低
价位住宅区与写字楼不存在同位模式,中等价位住宅区与写字楼在0~2 km范围内有同位模式,高价位住宅区与写字楼在4.8~6.3 km范围内有同位模式,这个结果说明北京五环内的写字楼大多分布在中高价位住宅区附近,中高價位住宅区与写字楼之间呈现集聚分布的现象,并且中等价位住宅区与写字楼之间的距离比高价位住宅区更近。
2) 居住地与地铁站点同位模式分析的结果表明:不同价位住宅区与地铁站之间都在0~2 km范围内具有空间同位模式,并且随着距离的增加,不同价位住宅区与地铁站的空间同位模式强度在不断减少,表明无论什么价位的居住地,地铁站点都会是影响其选址的因素之一。
3) 职住及地铁站点空间同位模式分析的结果表明: 虽然住宅区与地铁站和写字楼与地铁站都在中距离范围内具有空间同位模式,并且
随着距离的增加,空间同位模式的强度均在减小。但是,写字楼与地铁站点空间同位模式的强度要大于住宅区与地铁站点,这说明北京五环内的写字楼分布比住宅区更加靠近地铁站点,职业地的选择比居住地更加倾向于地铁站点。
综上所述,北京市五环内职住要素之间的同位模式以及职住要素与地铁站点之间的同位模式研究,为全面理解职住关系提供了新的视角,未来北京市在城市规划中应在注重功能分区的同时,要有意识
地鼓励在低价位住宅区附近配备写字楼,通过职住要素布局的优化配置,有效缓解职住不平衡的现象。
[参考文献]
[1]LOTWICK H W,SILVERMAN B W. Methods for analyzing spatial processes of several types of points[J]. The Royal Statistical Society,1982(B44):406-413.
