基于插值方法的温室温度场可视化仿真分析*
2021-02-22肖雪朋程曼袁洪波王起帆
肖雪朋,程曼,袁洪波,王起帆
(河北农业大学机电工程学院,河北保定,071000)
0 引言
温室是设施农业的重要组成部分,其内部小气候环境因子有温度、湿度、CO2浓度,光辐射强度等,其中温度是一个主导因素。温室内保持适宜的温度对作物健康生长非常重要,但是温室内温度空间分布不均衡,不同位置处的温度分布差异性大,复杂的温度分布模式不但导致其对热能的利用率也相对较低,而且还会使不同区域的作物生长情况产生差异,甚至降低综合产量。对温室温度的空间分布进行可视化仿真,可以直观的描述温度的空间分布状态,对于提高温室作物管理效率、环境调控和温室的结构优化的具有重要的现实意义[1]。
近些年,国内外学者进行了大量温室温度变化的研究,并建立了丰富的温室环境模型。总体来说,对于温室内温度变化的研究可以分为机理分析法和试验测量法[2]两种方法。机理分析法是一种基于理论的方法,机理分析法一般根据质量守恒方程和能量守恒方程,利用计算流体力学(Computational Fluid Dynamics,CFD)技术[3]进行分析和计算;主要用于研究温室在通风[4-6]、加温[7-9]、降温[10-12]等过程中温度场的变化情况,以及在此基础上的温室结构优化改进[13-14]如温室墙壁厚度及材料选择[15-18]、温室跨度选择[19-20]、排气孔结构和开口尺寸选择[21-23]等。机理分析法主要通过数值运算来进行温室小气候的模拟和仿真,计算过程繁琐且需要确定的参数众多,很多参数很难通过传感器进行测量,只能通过估算的方式进行近似计算,所以其计算精度直接受到这些参数取值的影响[24]。此外,温室在长期的使用过程中,有些参数如透光率、围护结构导热系数等参数会发生一定的改变[25],而这些变化难以量化,这些因素都会影响到机理法的计算结果。试验测量法主要通过各种测量仪器或传感器进行温室环境信息的获取,在此基础上对温室的墙体[26]、地面和空气的热传递[27],温室的温度分布[28]的进行研究。试验法得到的结果与其获取信息的传感器的精度和数量直接相关,为了得到较为精确的模型,需要搭建相对复杂的试验环境,对于不同的条件,可能还需要多次重复试验,成本投入大、试验周期长。将试验测量和机理分析方法结合,可以简化温室温度场分析的过程,简单快速根据温室数据构建模型研究温室温度环境的变化规律。
本文利用传感器采用数据,基于不同的插值方法对温室温度场分布进行了计算,并进行了温度场可视化仿真分析,比较了不同插值方法的优劣及其适用条件,为温室温度场分布规律研究提供了一种有益的方法。
1 材料与方法
1.1 试验地点与时间
试验地点为河北省保定市河北农业大学东校区,属于暖温带大陆性季风气候区。试验用温室为一面坡型钢架结构玻璃温室,坐北朝南,南偏西3°,东西方向长10 m,跨度为2.5 m,前屋面高2.1 m,后屋面高3.3 m。覆盖物为4mm浮法玻璃,透光率大于83%,地面水泥硬化,栽培模式为槽式基质栽培。温室主要能量来源为太阳辐射,试验时间为2019年7—9月,根据室外小型气象站气象数据选取典型晴天和阴天环境进行瞬时,短期,中长期的温度场的绘制。其中,8月11—12号为典型的阴天天气,温度为21 ℃~29 ℃,9月1—2号为晴天天气,温度为15 ℃~31 ℃,8月8—16号为短期的天气数据,包含晴天及降温的天气类型,8月30号—9月10号为长期的天气数据,包含多种天气情况。
1.2 试验环境构建
温室内温度采集使用温湿度传感器SHT20(湿度测量范围:0~100%RH,测量精度:±3%RH,湿度分辨率:0.1%RH;温度测量范围:-40 ℃~125 ℃,测量精度:±0.3 ℃,温度分辨率0.1 ℃)采集数据,测试之前对传感器进行校正。以温室东西方向1/2处温室剖面为主要测量平面,在垂直方向共设置了0 m、0.35 m、1.2 m、2 m四个高度层面,水平方向设置0 m、0.4 m、0.8 m、1.2 m、1.6 m、2 m、2.5 m七个层面。每层均匀分布7个传感器,温室顶部均匀分布5个传感器,共33个温度传感器,同时测量1.8 m处太阳辐射强度。玻璃温室示意图如图1所示。温室内部太阳辐射由JTBQ-2总辐射传感器(光谱范围:280~3 000 nm,测量范围:0~2 000 W/m2,准确度±2%,灵敏度7~14 μV/(W/m2))采集。外界温度与光照由气象站采集记录。
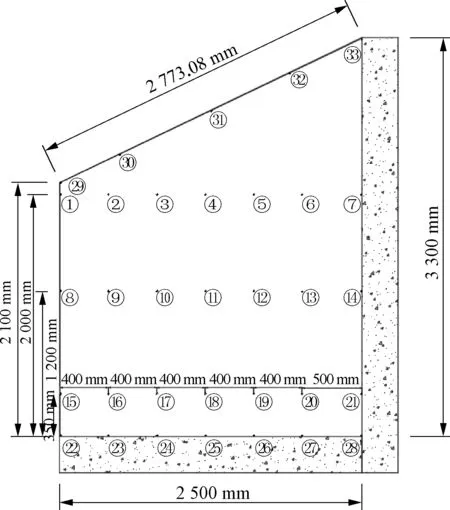
图1 传感器部署示意图
1.3 试验环境构建
温度采集与处理功能主要由STM32单片机实现,单片机通过引脚控制传感器采集数据,然后将信号处理后通过串口输出环境参数数据。所有测量数据的采集间隔为10 min,数据上传至电脑储存。电脑将数据储存为txt文件,可以实时储存数据及查阅历史数据。
1.4 数据分析方法
数据处理采用Matlab2018a,运算平台计算机的配置为:CPU为AMD R-2600主频3.8 GHz,内存为DDR4频率3 000 Hz容量16 G。根据采样点收集的温度数据,使用插值算法对数据进行扩充,实现温度场的拟合和图像绘制。
插值是在一组已知数据点的范围内添加新数据点,而且函数运算结果穿过样本数据点的技术。使用插值算法可以实现填充缺失的数据、对现有数据进行平滑处理以及进行预测等功能。根据样本数据的结构,插值分为两类:插入网格数据(meshgrid),数据部分为轴对齐网格格式的样本数据,数据格式要求为有序数据。内插散点数据(griddata),数据部分为散点格式的样本数据,数据中的点没有结构或其相对位置间的顺序要求。由于网格上的数据插值运算时,数据不能缺失,要求数据为标准的矩阵。也不容易按实际比例显示空间温度分布。当数据类型标准时采用网格的数据点和散点数据点插值结果相同。散点插值方便查询坐标上的数据灵活性更强。综合考虑采用散点插值的方式。
插值运算过程分为几个步骤:(1)创建散点数据集。(2)创建Delaunay三角剖分,并查询插值点位置(查询点是griddata执行插值的位置)。(3)选择插值方式计算。通常情况下,整个插值过程通过一次函数调用完成,插值结果曲面始终穿过x、y和z定义的数据点即样本值v。
散点插值中数据样本点的样本值v与坐标中x、y和z空间位置对应,样本点唯一。以温室的地面东北角为空间原点,建立传感器的空间坐标,确定传感器的空间位置。
在进行散点插值前对数据预处理进行划分,构建三角剖分数据结构体使数据相对合理的分配以求包围查询点。三角剖分是指几何中将平面对象细分为三角形,并且可以通过类似的扩展将高维度的几何图像细分为二维的三角形。划分结果满足所有的面均为三角面且没有相交的边、三角面内不含数据点(端点除外)、所有三角面组成数据的凸包。
根据插值数据的需求,在划分的三角形中找到查询点位置,计算值取决于后续步骤的插值算法。散点插值提供5种运算方式,如表1所示。
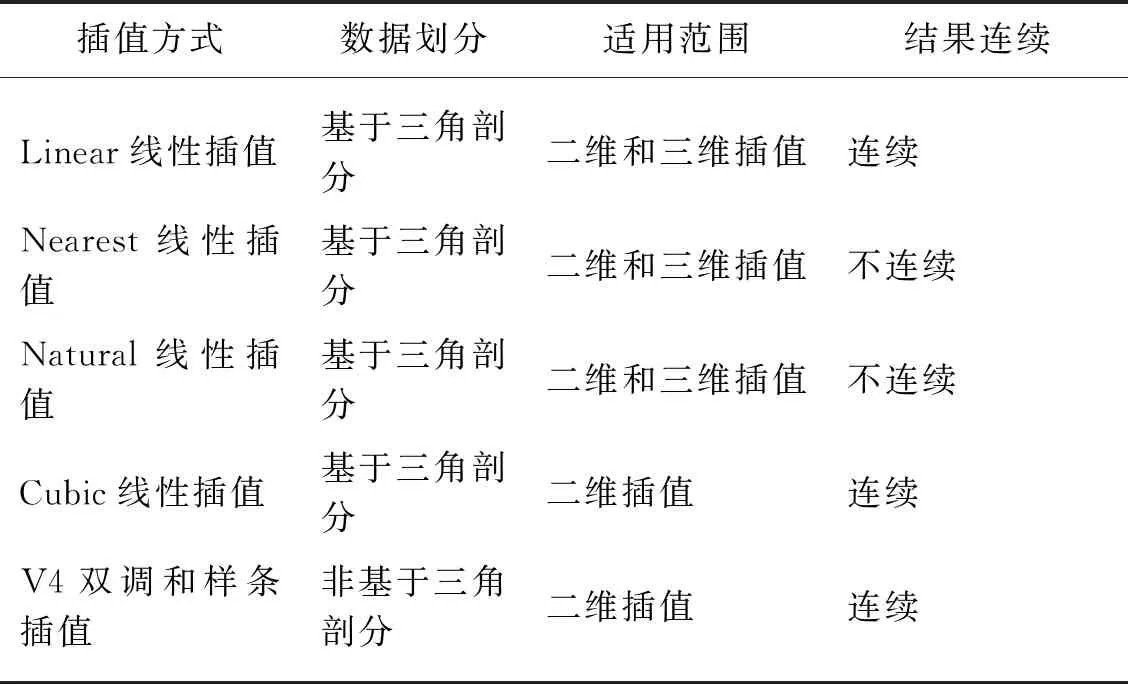
表1 散点插值方式区别
1.5 插值运算结果
在MATLAB中调用插值函数将空气温度数据3×5差值为6×10,对比实际测量值与插值数据区别。MATLAB编程:vq=griddata(x, y, z, v, xq, yq, zq, method),method可以根据插值方式选择‘Linear’、‘Nearest’、‘Natural’、‘Cubic’或‘V4’。

表2 原始数据
Linear线性插值在查询点插入的值是基于三角网结构体顶点样本邻点数值的线性插值。已知两数据点坐标用直线连接,以求在直线上其他的点进行插值计算。表3为Linear插值数据结果。

表3 Linear插值数据
Nearest最近邻点插值在查询点插入的值是距三角网结构体顶点样本最近的值。已知插值点的坐标与两数据点间的空间位置,选取与插值点距离近的数据点数值为插值结果。表4为Nearest插值数据结果。

表4 Nearest插值数据
Natural自然邻点插值在查询点插入的值是基于三角网结构体临近点对查询点的贡献率计算的插值结果。自然邻点插值时先对所有样本点创建泰森多边形,当对未知点进行插值时,就会修改这些泰森多边形并对未知点生成一个新的泰森多边形。表5为Natural插值数据结果。

表5 Natural 插值数据
Cubic三次插值在查询点插入的值基于三角网结构体顶点样本邻点数值的三次卷积插值结果。根据已知数据构造出三次多项式,用构造多项式的极小点逼近寻求已知点函数的极小点的方法,求构造多项式导数为零的根,作为已知点函数的极小点的近似,重复应用这一方法进行迭代计算,直到得出满足事先给出的精度要求为止,然后进行插值。表6 为Cubic插值数据结果。

表6 Cubic 插值数据
V4插值方式数据划分非基于三角剖分,采用的是MATLAB自定义的4个样本点进行样条函数插值方式。表7为V4插值数据结果。

表7 V4插值数据
Cubic和V4方法生成平滑曲面,而Linear和Nearest分别具有零阶导数和一阶导数不连续的特性。Nearest插值方式不符合空气温度渐变的规律,最后选择Cubic,Linear,Natural,V4这四种方式对比。
试验过程:(1)将储存的环境数据由TXT转换成Excel文档。(2)在Matlab编程,导入传感器空间分布数据,环境数据。(3)设置多核并行运算,插值运算类型,运算精度等参数。(4)输出温度场平面图,运算时间,及数据保存。
2 结果与分析
2.1 插值数据量确定
将温度数据经过图像化处理形成温度分布图片,可以直观、迅速、准确地呈现出温室内部温度的分布规律,为进行温度调节研究提供方便。数据量的大小决定着画面的清晰度和预测数据的准确性,同时影响着运算速度。首先需要确定适宜的插值后数据量,插值数据量可以由式(1)计算得到。
Number=(T_max-T_min)/Scale
(1)
式中:Number——插值数据量;
T_max——进行插值计算时传感器测量的最高温度;
T_min——进行插值计算时传感器测量的最低温度;
Scale——传感器分辨率。
选取2019年9月1日温室的环境数据,同一时刻测量平面最高温度和最低温度最大差值20 ℃,根据传感器分辨率0.1 ℃,由于试验温室主要测量面近似方形,最高温度出现在南侧附近和最低温度出现在北侧墙体,横向、纵向插值产生的200×200数据生成图片。然后分别生成7×7,25×25,50×50,100×100,400×400的数据量生成图片,将图片保存成相同大小。在Matlab中将图片灰度化化,逐像素点比较相似。结果如图2不同算法插值数据量与数据可视化后相似度关系曲线,当数据为200×200时四种方式相似度均超过95%。图3为不同插值方式200×200与400×400灰度图,从图片中已经看不到差别,可以认为200×200的数据量满足图形绘制要求。

图2 不同算法插值数据量与数据可视化后相似度关系曲线
2.2 相同天气下不同插值方式的温度数据的比较
为了比较不同插值方式的温度数据的准确性,采用插值与实际采集值对比的方式。9月1—2日为典型的晴天天气(2019-09-01日最高温度31 ℃最低温度15 ℃晴南风微风;2019-09-02日最高温度31 ℃最低温度15 ℃西南风2级),8月11—12日为典型的连阴天天气(2019-08-11日最高温度26 ℃最低温度21 ℃,东北风4级;2019-08-12日最高温度29 ℃最低温度21 ℃东北风3级)将数据中各点依次删除。利用剩余数据对该点进行预测,计算值与测量值差值反映运算方式的准确性,由于删去1个数据点时对图片的整体影响过小,采用坐标点取值的方式,取值与采集值做差,得到的数值取绝对值,最后计算每个点不同时间段的平均值,间隔半小时计算一次。数据处理结果如表8所示,晴天数据中最大值61.9 ℃,数据中最小值24 ℃,平均值38.8 ℃,阴天数据中最大值37.0 ℃,数据中最小值25.3 ℃,平均值30.2 ℃。结果显示:空气温度尤其是空间中心位置的插值数据误差较小,地面、墙体、覆盖物周围的温度数据插值数据误差较大,可能由于壁面温度与气温相差较多,导致经过插值运算误差较大。Cubic插值方式误差最小,V4插值方式误差最大,Natural和Linear相似。地面附近数据误差较大。
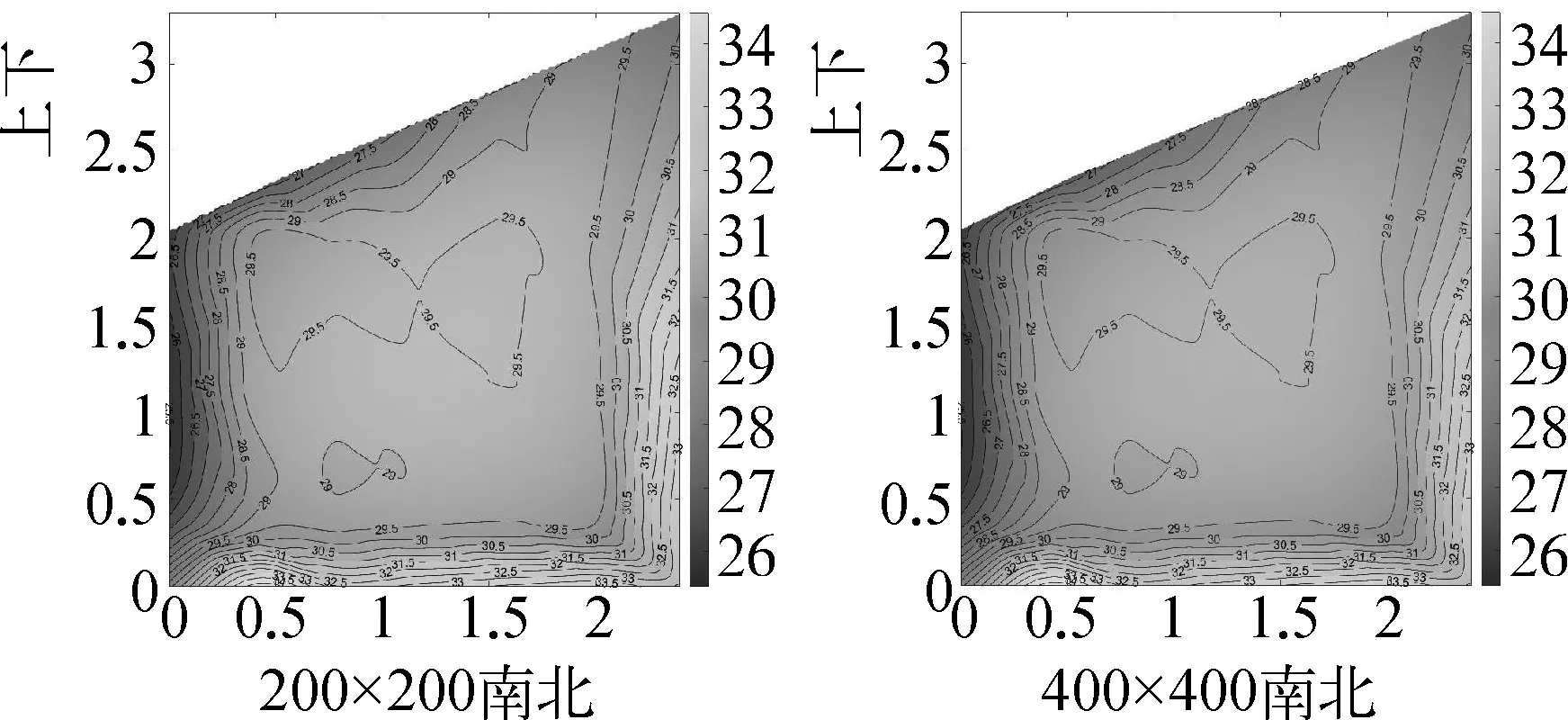
(a) Cubic插值方式200×200与400×400灰度图
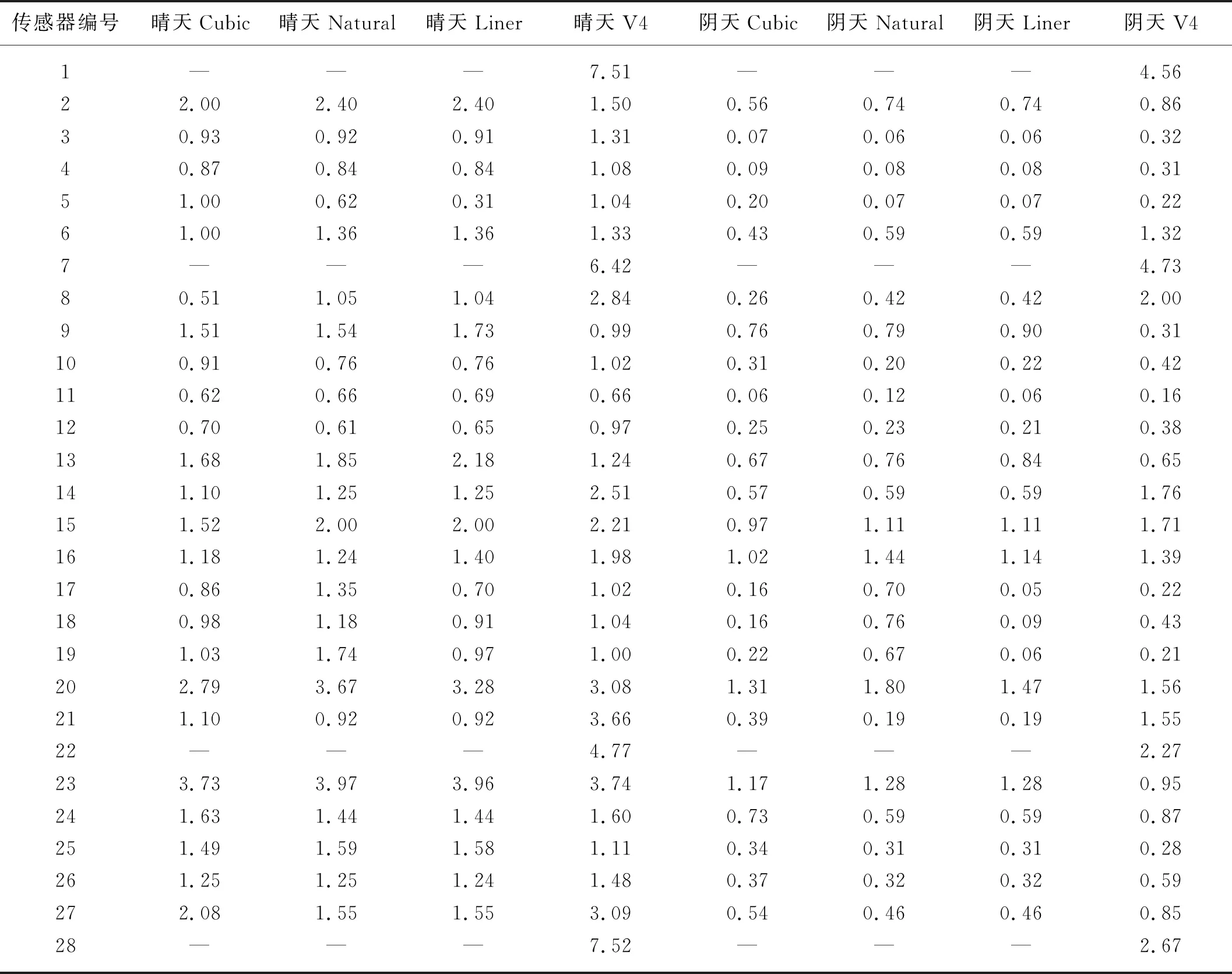
表8 不同插值算法数据误差
2.3 不同天气数据下不同插值方式的温度数据误差平均值的比较
误差平均值如表9所示,晴天时由于阳光充足温室效应明显,温度变化较剧烈。不同部位的温室壁面接受到的辐射不同,空气与壁面温差较大,导致误差的平均值增大。阴天温度变化平缓,温室空气、壁面温度在小范围内变化,误差平均值小。晴天两天,一周、两周、三种环境预测数据误差平均值相似。总体四种环境预测数据误差平均值中:Cubic、Natural、Liner误差平均值明显小于V4误差平均值。数据中最小值25.3 ℃,平均值30.2 ℃。结果显示:空气温度尤其是空间中心位置的插值数据误差较小,地面、墙体、覆盖物周围的温度数据插值数据误差较大,可能由于壁面温度与气温相差较多,导致经过插值运算误差较大。Cubic插值方式误差最小,V4插值方式误差最大,Natural和Linear相似。地面附近数据误差较大。
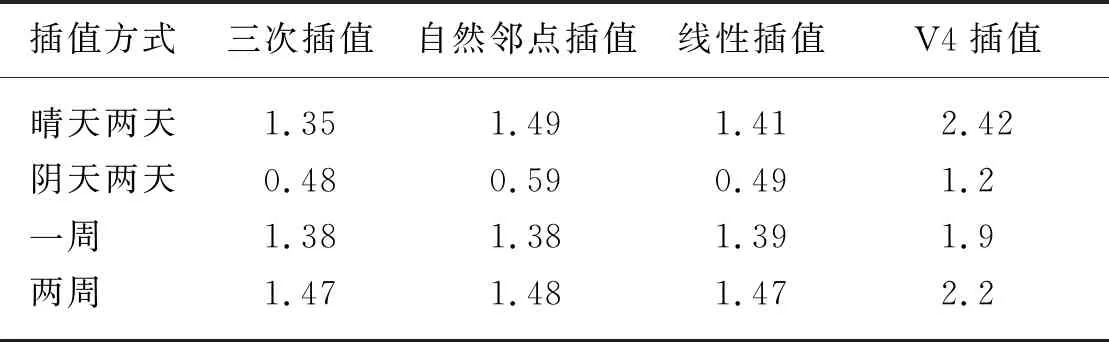
表9 误差平均值
2.4 不同插值方式运算时间的比较
不同插值方式运算对计算机的资源占用存在差别。Matlab中并行运算可以减少运算时间,但是选择合适的运算方式也十分重要。采用相同的程序框架,读取环境数据、传感器位置数据、对数据加工形成矩阵、设置图片的输出样式、只改变插值方式,比较运算时间。数据量采用200×200大小,运算三次取平均值,运算时间结果如表10所示。结果显示夜晚温度差异较小、运算温度范围小、计算量小时间短,中午温室内温度分布不均,中午温度差异较大、运算温度范围大、计算量大运算时间较夜晚运算时间长。总体运算时间Liner运算时间最短,V4运算时间最长,Cubic和Natural处于两者之间。
2.5 不同插值方式可视化比较
图4为温室不同插值方式温度场分布。Cubic插值方式结果等温线平滑,温度变化平缓。Liner插值方式结果等温线粗糙,等温线存在突变情况。Natural插值方式结果处于两者之间, V4生成的温度场分布图与其他三种方法的结果有着显著的不同,壁面与空气之间没有变化趋势,与实际情况存在较大差距,表明该方法不适用于温度场插值化的可视表达。
图5为2019年9月1日玻璃温室不同插值方式温度最低时刻温度场分布。夜晚,没有加温时,热源是地面、墙体的蓄热。热损失主要有三部分:通过地面沿横向传到室外地面;通过缝隙传到室外空气;温室内的空气以对流辐射和凝结等方式,向覆盖材料的内壁面传导,通过热传导方式再扩散到覆盖材料的外表面,之后再以辐射方式散失到周围。形成地面、墙体附近温度高,覆盖物玻璃附近温度低温,室内部大部分空气温度均匀的情况。Liner和Natural插值结果相似,靠近墙体部分出现了温度变化梯度,Cubic插值结果在温室上部出现了温度分布温度变化梯度,符合热空气上升的自然规律,V4插值结果温室范围内,顶部出现高温区域不符气温变化规律。

(a) Cubic插值温度场
(a) Cubic插值温度场
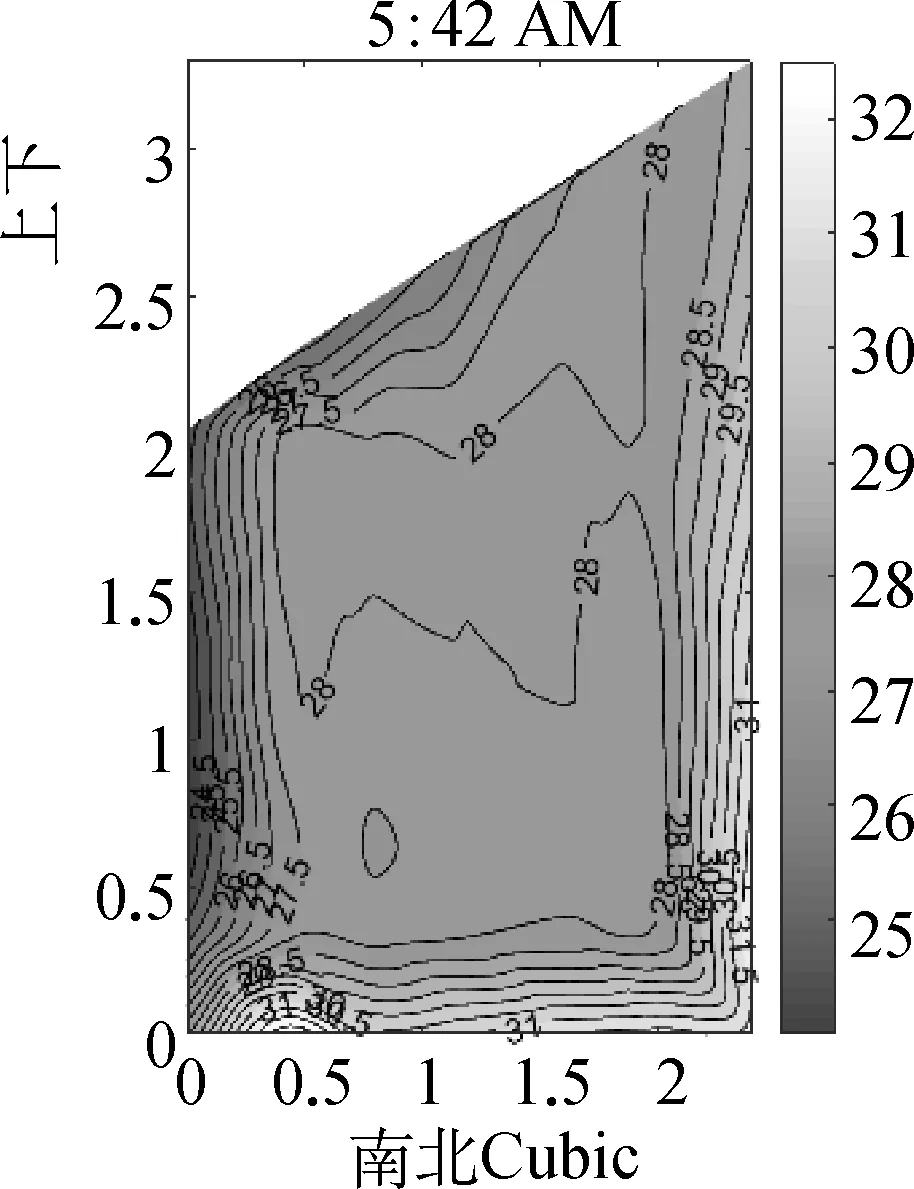
图6为2019年9月1日玻璃温室不同插值方式早上日出时刻温度场分布。早晨太阳升起,温室效应使温室内渐渐升温,升温从温室下部地面附近开始。温室内部的空气温度基本相同,内部的温度分布较为稳定。对比夜晚的温度数据,壁面与空气均有明显的温度升高。Liner和Natural插值结果相似,地面附近温度较高,室内空气大部分温度均衡,Cubic插值结果在南侧出现了部分高温区域,空气升温从南部开始, V4插值结果温室范围内,顶部、南部出现高温区域。
图7为2019年9月1日玻璃温室不同插值方式中午温度最高时刻温度场分布。
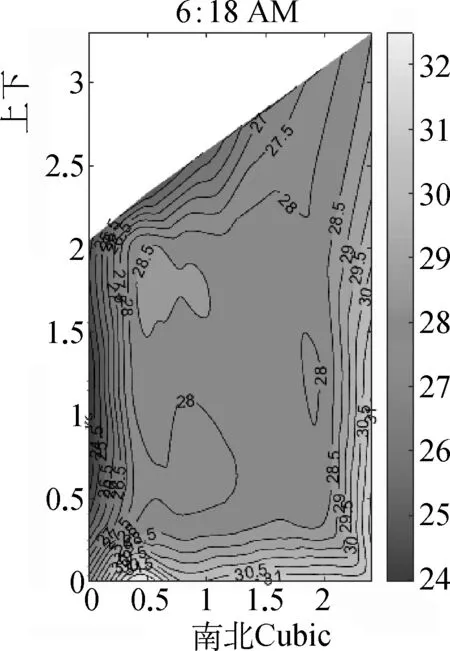
(a) Cubic插值温度场

(a) Cubic插值温度场
从图7可以明显看出温室南侧靠近玻璃区域为高温聚集区,而北侧墙体的位置温度较低,说明在中午,南侧位置由于优先接收太阳辐射而且辐射较强,空气温度明显高于墙体;温室上部温度较低的原因可能是由于温室上部的建筑物遮挡,影响了光照条件,温度在水平方向上中间高、北侧较低,在竖直方向上部高、地面较低,Cubic、Liner和Natural三种方式插值结果相似,V4上部同样出现高温与其他三种方式存在差别。
图8为2019年9月1日玻璃温室不同插值方式下午日落时刻温度场分布。傍晚时,太阳下落太阳辐射减少。温室内地面、墙体温度大于覆盖物的温度,室内空气处于降温的状态,温度较为均匀。Cubic插值结果在下部出现了部分高温区域,空气接近地面和墙体时温度较高。Liner和Natural插值结果相似,Liner插值结果出现温度突变,V4上部墙体同样出现高温,中下部出现低温。
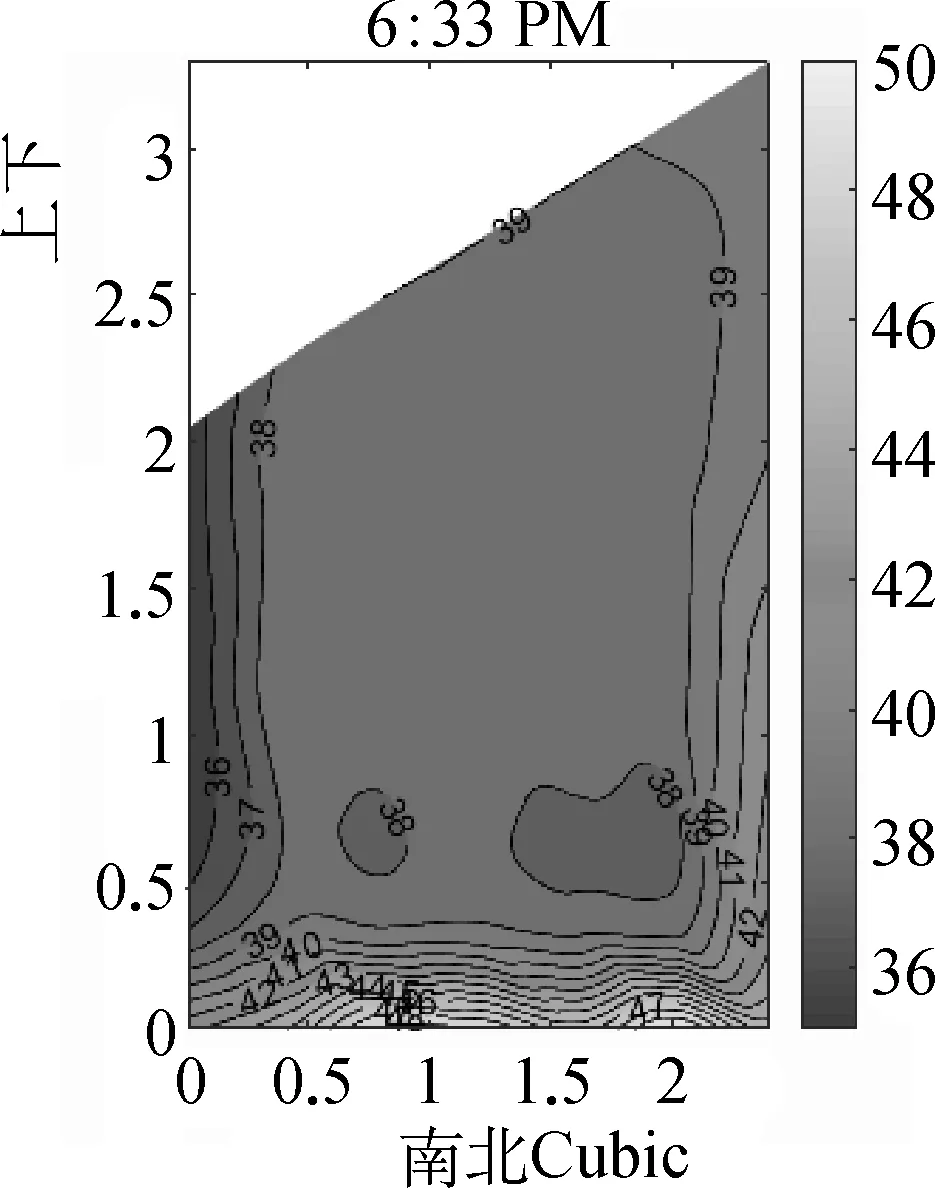
(a) Cubic插值温度场
3 结论
借助MATLAB平台高效的数值计算及完备的图形处理功能,对获取的大量温度数据进行批预处理。将数字数据经过图像化处理转化为温度分布图,是数据可视化方面重要的方式。不同插值运算结果的温度场研究总结如下。
1) 插入数据量以传感器精度和温度差为依据,插值结果可以反应温室内的温度场细节,图片边缘较为顺滑,运算量适宜。
2) 不同的天气情况对插值的误差影响较大,与温度的波动范围有关。Cubic、Natural、Liner插值运算的误差结果近似,平均误差均在1.5 ℃内,且均小于V4。
3) Cubic、Natural、Liner三种插值方式中,Cubic运算时间最长,Natural运算时间其次,Liner运算时间最短,平均每次运算2.816 s,需要大量温度场图运算时Liner插值方式较为适宜。
4) Cubic插值运算输出图片温度变化平滑,且具有温度的水平梯度,接近温室温度的变化规律效果好。图片能够较好地反映出温室的温度场。Cubic插值方式适用于展示研究某一时刻的温度场。
