考虑计算延迟的Boost变换器异步切换控制方法
2021-02-22王荣浩
王荣浩
(中国人民解放军陆军工程大学国防工程学院,南京 210007)
电能是保障电气设施设备有效运行的最重要的能量形态,是电气设备正常工作的基础能源. 不同的电气设备对电压等级的需求也不同,直流供电系统中电压等级的变换主要依靠直流DC-DC变换器. Boost电路作为直流变换器的主要拓扑结构,具有体积小、效率高等优点. 此外,为了提高电能质量,电气设备输入侧普遍采用功率因数矫正技术,而Boost电路是常用的功率因数矫正装置的主拓扑电路. Boost电路拓扑在供配电系统及电气设备中的应用越来越广泛. 文献[1]根据混杂切换理论建立Boost功率变换器的混杂模型,分别讨论变换器在连续模式(CCM)和断续模式(DCM)两种工作模式下的切换控制方法. 文献[2]阐述了利用分段仿射切换模型对Boost变换器进行建模的方法,并概括了以此模型为基础的公共Lyapunov函数、多Lyapunov函数以及模型预测控制方法. 文献[3]建立了用于储能节能系统的双向DC-DC变换器切换系统模型,构造了系统的Lyapunov函数,通过Lyapunov函数推导出系统切换控制律. 文献[4]引入混杂系统理论,建立了基于切换系统的开关变换器统一模型,基于该模型的参数矩阵,提出系统Lyapunov 函数的构造方法,通过构造Lyapunov 函数得出系统切换律,分析该切换律条件下系统在切换平衡点的稳定性,并总结出建立该统一模型的一般方法和具体步骤. 文献[5]建立了Boost变换器的切换仿射线性系统模型,然后根据凸组合稳定条件及无源性理论,基于公共Lyapunov函数方法构造切换律,保证系统在任意切换下的二次稳定性. 文献[6]基于Lyapunov稳定性理论,利用线性矩阵不等式(LMI)优化方法设计了Boost变换器的切换控制器参数,相比于传统PI控制方法,所提出的切换策略具有更强的参数鲁棒性和暂态过程的快速性. 文献[7]研究了一种有限时间弹性切换控制方法并用于Boost变换器电路模型的控制,实验结果表明电压能够在有限时间内收敛至平衡态附近,比渐近稳定控制具有更加良好的暂态特性. 文献[8]基于切换系统的公共Lyapunov函数方法研究了Boost变换器电路的二次稳定性,基于该稳定性的控制器允许电路参数在一定范围内波动,具有较强的鲁棒性.
综上,目前采用切换系统建模及分析方法是研究Boost变换器电路稳定性的有效手段. 基于切换系统处理方法进行Boost变换器的分析和设计相较于传统的小信号平均模型方法更能够体现变换器的本质特征. 然而,实际的Boost变换器控制电路广泛采用数字控制器,目前已有的基于状态切换控制理论的Boost变换器分析和设计均不考虑占空比控制律的计算时间. 由于数字控制在计算占空比时需要计算时间,当前开关周期计算所得到的占空比可能用于下一个开关周期,因此会产生数字延迟. 若在设计控制器时对此估计不足,在实际应用中输出电压很可能会出现较大纹波甚至产生混沌分岔现象[9],使得理想状况下的分析和设计方法失去原本的稳定控制效果. 已有文献在用切换系统处理方法研究Boost变换器控制电路时很少考虑控制作用和模型切换之间的这种延迟现象. 对于控制的延迟效应在切换系统研究领域称为异步切换控制模式[10]. 此外,数字控制延迟效应的存在会导致系统稳定时间变长,甚至状态失稳,而有限时间控制能很好地提升系统的暂态性能指标,且确保系统响应的快速性[11]. 因此,利用有限时间异步切换控制方法研究Boost变换器的稳定性问题具有重要意义.
本文根据切换系统异步控制理论对Boost变换器进行建模并控制,检测电感电流值和电容电压值,并利用多Lyapunov函数和平均驻留时间方法计算占空比来控制功率开关器件的动作,从而实现Boost变换器的有限时间混杂状态切换. 当控制律所依赖的电路模型的切换和晶体管的开关动作之间存在延迟时,利用异步切换控制方法对延迟效应进行了分析与估计,进而减少了输出电压的高频振动,具有良好的控制性能.
1 Boost功率变换器异步切换建模
Boost开关变换器电路结构如图1所示,其中L为电感值,iL为流经电感的电流瞬时值;C为电容值,uC为电容两端的电压瞬时值;R为电阻阻值,v0为电阻两端的瞬时电压;D和T分别为钳位二极管和晶体管;E为外部输入电压值. 当晶体管处于导通状态时电路的拓扑如图2所示. 此时电感两端产生输入电流,电源通过电感向电容两端充电. 位于电容和电感之间的钳位二极管可防止电容对地放电. 在直流电输入作用下,电源对电容的充电

图1 Boost变换器电路原理图

图2 Boost电路充电过程
过程使得流经电感的电流会成比例地线性增加,通常这个比例由电感值来决定. 流经电感的电流不断增加使得电感处于持续储能状态.
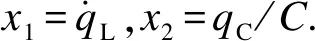

(1)

(2)
当晶体管处于截止状态时,此时由于电感中储存了一定能量,电感会通过钳位二极管向电容两端充电,电感自身处于放电过程,由于流经电感两端的电流不会发生突变,因此电流值不会瞬间变为零,而是由充电过程结束时的电流值缓慢降到零. 电感自身的放电过程使得电容两端电压不断升高,最终导致输出电压值超过输入电压,至此升压过程完毕. 晶体管截止时的等效电路如图3所示.

图3 Boost电路放电过程

(3)
综合式(2)和(3)可得
(4)
式中,u在{0,1}上取值. 定义拉格朗日函数
(5)
代入拉格朗日方程
(6)

(7)
整理得
(8)

(9)
由此可得,Boost开关变换器在晶体管导通和截止时具有2种不同的电路状态模型,通过控制晶体管的通断,Boost电路在2个不同的状态方程间切换,即
当u=1时
(10)
当u=0时
(11)
Boost开关变换器模型可以用更一般的切换系统方程描述,即
(12)
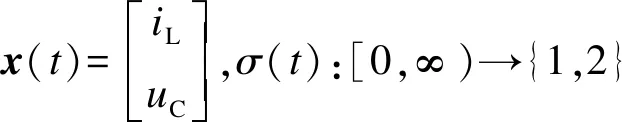
S′={(t0+Δ0,σ(t0)),(t1+Δ1,σ(t1)),…,
(tk+Δk,σ(tk)),…}
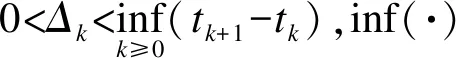
(13)
与式(12)不同的是,模型式(13)考虑了由切换控制律计算时间导致的晶体管开关触发动作的延迟效应,该异步切换模型更具有实际意义.
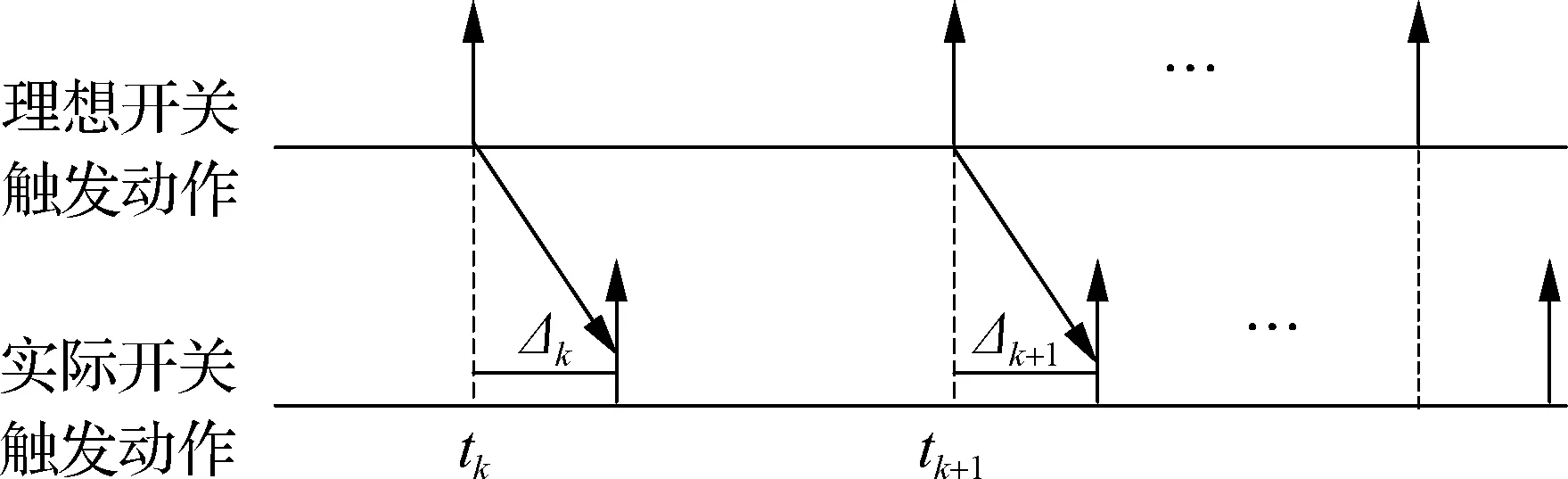
图4 开关电路异步触发模式
2 有限时间异步切换控制方法
针对式(10)和(11)所描述的切换状态方程,已有文献多采用传统的基于状态切换控制方法研究输出电压的稳定性问题,即依赖实时检测到的iL和uC值构造系统的切换律,从而控制晶体管的导通或截止. 这种方法最大的缺陷是无法获取系统切换的时间信息,基于状态的切换假定状态量的检测和控制律的计算是瞬时完成的,在实际应用中计算时间延迟会导致当前的控制律和系统模型切换之间出现不匹配,经过控制作用的周期性累积,最终使得系统出现无法预知的控制效果. 而依赖时间的切换控制方法基本思想是通过限定切换频率达到系统稳定的效果,由于其建立在时间度量基础上,因此能够对计算时间做出估计并实施控制,可以有效避免计算延迟带来的控制效果恶化以及由此产生的无法预知的后果.
不失一般性,针对式(13)讨论系统的稳定性. 首先给出系统驻留时间和有限时间稳定的相关定义.
定义1[12]对于任意的切换信号σ(t)和t2>t1≥0,用Nσ(t1,t2)表示在时间段[t1,t2]上σ(t)的切换次数,对于给定的N0≥0和τa>0,若有如下关系式成立:
则正常数τa称为平均驻留时间,非负常数N0称为振动幅度. 由于N0是固定常数,如文献[13]所述,本文选择N0=0.
平均驻留时间反映了开关电路在一段时间内的切换频率,其定义表明为了保持稳定性,系统在某个时间段内切换频次需限定在一定范围内,不宜过高. 实际上过高的切换频率是导致开关电路产生混沌的根本原因[14].
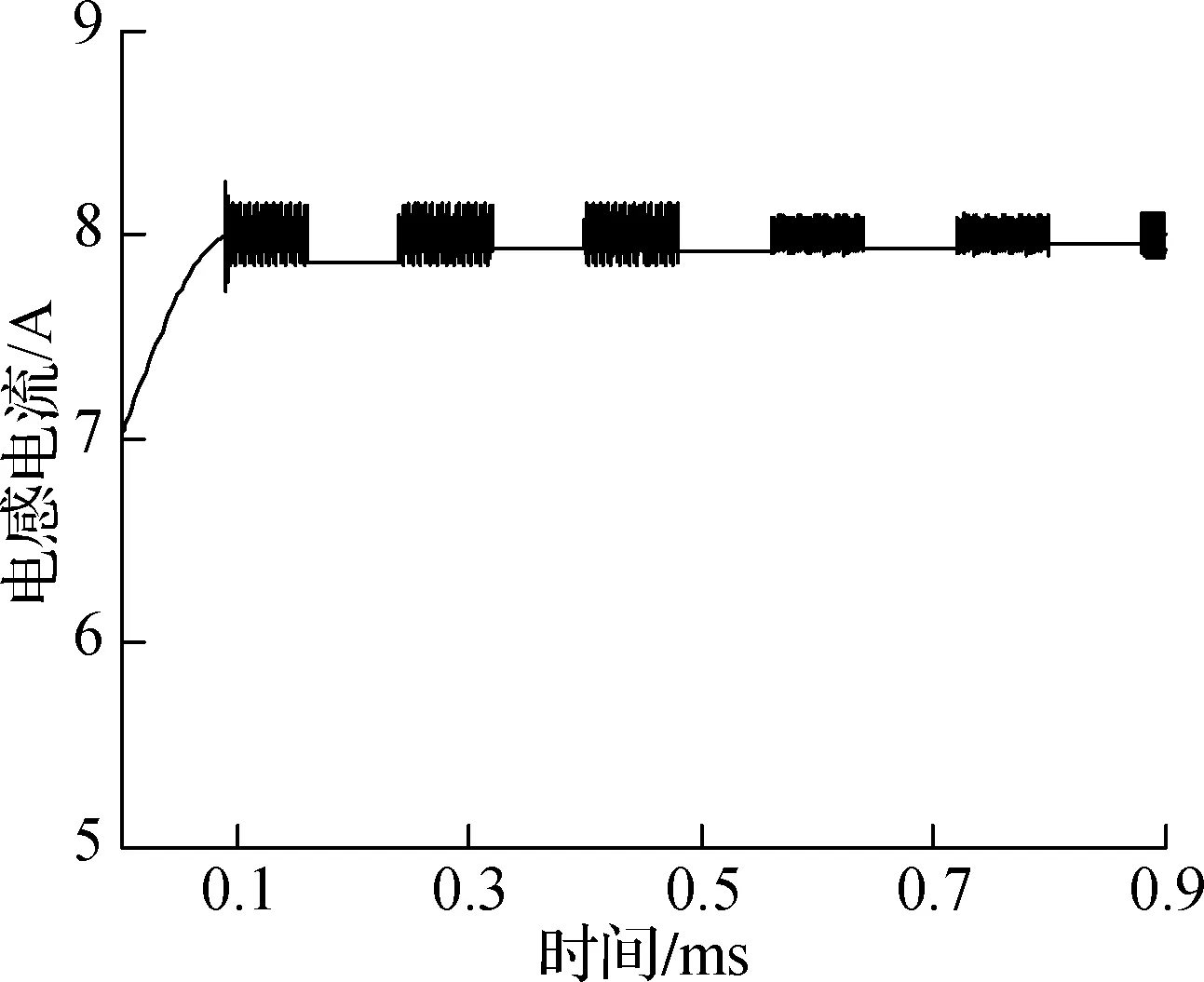
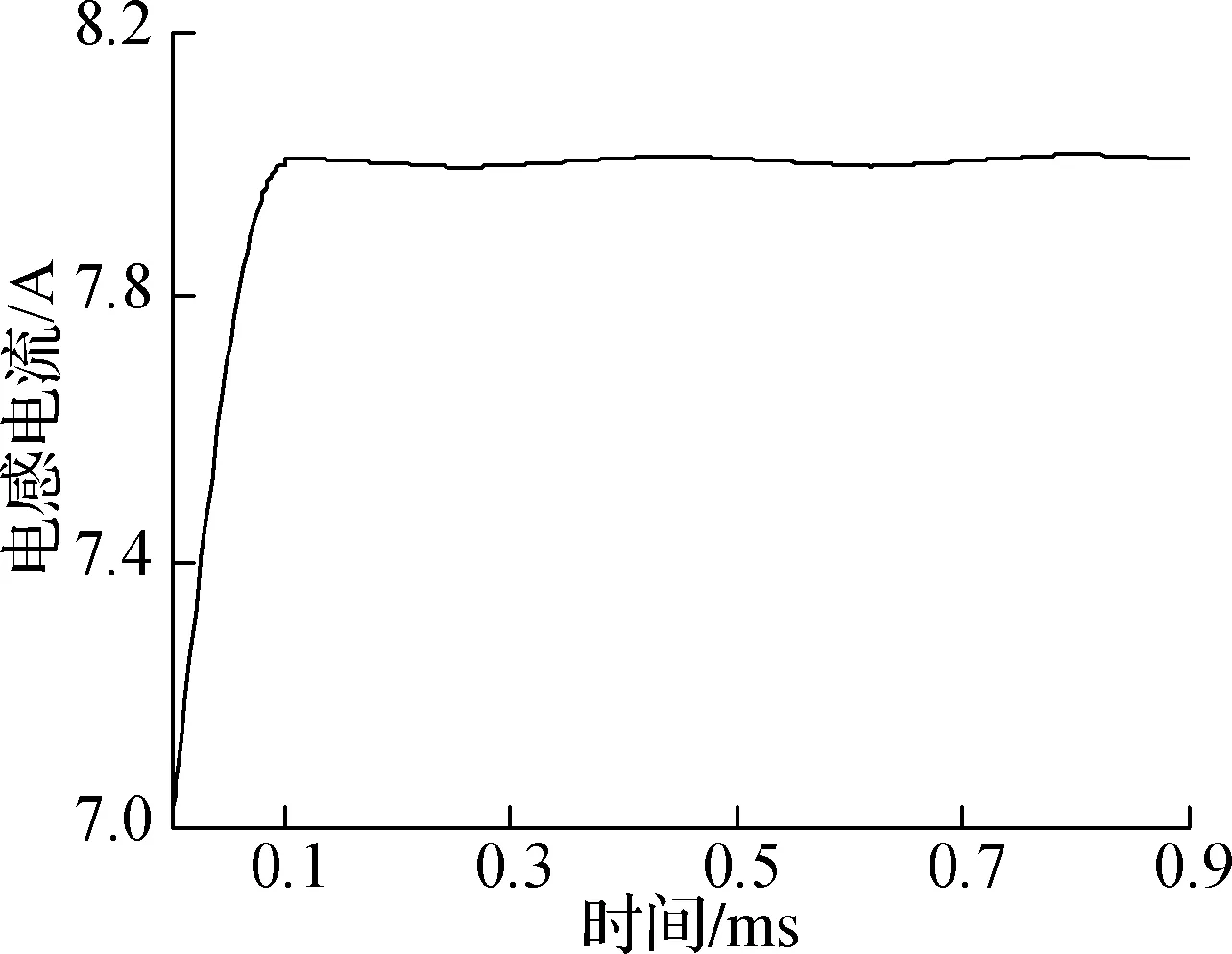
定义2给定正常数c1、c2、Tf和切换信号σ(t)(c1 (14) 式中,fi(·):Rn→Rn(∀i∈N)为非线性连续函数,若系统状态满足‖x(0)‖≤c1⟹‖x(t)‖ 有限时间稳定性定义给出了电路系统在指定时间段内的状态特性,相较于传统的渐近稳定性更关注于系统暂态性能指标,且能够确保电路输出响应的快速性. 考虑式(13)的非切换形式: (15) 式中,A∈Rn×n,B∈Rn×1为非切换形式下的系统参数矩阵.式(15)的行为轨迹可由如下结论来描述. 引理环C1:={x:xTx≤c1}和C2:={x:xTx≤c2}是系统式(15)的给定状态域,若存在正常数ξ>0、正定矩阵P>0使得 ATP+PA≤ξP (16) 且参数c1、c2满足 (17) 式中,λmax(·)和λmin(·)分别表示矩阵的最大和最小特征值,则当 (18) 对于初始状态x0∈C1,x0=x(0),式(15)的所有轨迹满足x(t)∈C2,∀t∈[0,Tf]. 证明对于系统式(15),构造候选Lyapunov函数 V(t)=xT(t)Px(t) 则所构造的Lyapunov函数关于时间t的导数满足 ξλmax(P)‖x‖2+2‖x‖‖PB‖ (19) 在状态域C2:={x:xTx≤c2}中,对式(19)两边积分可得 (20) 当t∈[0,Tf],‖x0‖≤c1时,有 λmax(P)‖x0‖2+c2[ξλmax(P)c2+2‖PB‖]Tf≤ (21) ‖x‖≤c2 (22) 由此可得 (23) 因此‖x(0)‖≤c1⟹‖x(t)‖≤c2,∀t∈[0,Tf]. 证毕. 式(23)针对一般的非切换系统给出了系统稳定运行时间与系统运行状态界之间的定量关系,作为特例当切换系统只含单个子系统时,系统稳定运行时间随允许的运行状态界c2的增大(减小)而增大(减小). 引理中的式(16)和(17)揭示了单个系统有限时间稳定时系统参数需要满足的条件,该条件将被扩展至切换系统的情形,且引理证明中式(21)所揭示的单个系统Lyapunov函数任意时刻值与初始值之间的关系将被用于切换系统有限时间稳定定理的证明. 进一步讨论切换情形下的有限时间控制方法,对于切换系统式(13),给出如下有限时间异步切换控制律的设计定理. 定理环C1:={x:xTx≤c1}和C2:={x:xTx≤c2}是系统式(13)的给定状态域,若存在正常数ν+,ν->0,ρ1,ρ2>1和正定矩阵Pi,Pj,Pij>0(i,j∈N,i≠j)使得 (24) (25) Pj<ρ1Pij,Pij<ρ2Pi (26) 且有 (27) 式中 式中,Δ[0,Tf]表示在时间段[0,Tf]上占空比的总计算时间,且系统平均驻留时间满足 (28) 则对于初始状态x0∈C1,式(13)的所有轨迹满足x(t)∈C2,∀t∈[0,Tf]. 证明由开关电路异步触发模式可知,当第i个子系统在时刻tk切换到第j个子系统时,有σ(t)=i,t∈[tk-1,tk)和σ(t)=j,t∈[tk,tk+1),则实际开关触发动作可表示为σ′(t)=i,t∈[tk-1+Δk-1,tk+Δk)和σ′(t)=j,t∈[tk+Δk,tk+1+Δk+1). 选择如下分段类Lyapunov函数: (29) (30) 式中,Vj为第j个子系统在时间段tk+1-tk-Δk内的类Lyapunov函数;Vij为第i个子系统切换到第j个子系统时在时间段Δk内的类Lyapunov函数;Θk-=‖PjBj‖,Θk+=‖PijBj‖. 根据切换信号σ(t)和σ′(t)与子系统序号的关系可得 Vσ′(tk+Δk)(tk+Δk)≤ρ1Vσ(tk-1)σ(tk)((tk+Δk)-) (31) 记ζk-=ξ-c2+Θk-,ζk+=ξ+c2+Θk+,则由式(26)和(30)得 V(t)≤V(tk+Δk)+c2ζk-(t-tk-Δk)≤ ρ1ρ2[V(tk-1+Δk-1)+c2ζ(k-1)-(tk-tk-1- Δk-1)]+ρ1c2ζk+Δk+c2ζk-(t-tk-Δk)≤ (ρ1ρ2)ρ1V(tk-1)+ρ1ρ2ρ1c2ζ(k-1)+Δk-1+ ρ1c2ζk+Δk+c2ζk-(t-tk-Δk)+ρ1ρ2c2ζ(k-1)-· (tk-tk-1-Δk-1)≤…≤(ρ1ρ2)kρ1V(0)+ (ρ1ρ2)kρ1c2ζ0+Δ0+(ρ1ρ2)kc2ζ0-(t1-t0-Δ0)+ (ρ1ρ2)k-1ρ1c2ζ1+Δ1+(ρ1ρ2)k-1c2ζ1-(t2-t1- Δ1)+…+ρ1c2ζk+Δk+c2ζk-(t-tk-Δk) (32) 记Θ-=max{Θ0-,Θ1-,…,Θk-},Θ+=max{Θ0+,Θ1+,…,Θk+},则由式(32)可得 (33) 由平均驻留时间的定义,在时间段[0,Tf]内系统的总切换次数为k+1=Nσ(0,Tf)=Tf/τa,则在时间段[0,Tf]内有 (34) 基于式(29),对于∀i,j∈N,i≠j有 (35) 且 (36) 由于 ‖x(0)‖≤c1 (37) 则有 (38) 由式(34)和(38),如下关系式成立: (39) 由式(39)可知,若 (40) 则可确保‖x(t)‖ 特别地,当Δ[0,Tf]=0,即理想状况下不考虑占空比控制律的计算时间,则有如下推论. 推论环C1:={x:xTx≤c1}和C2:={x:xTx≤c2}是系统式(13)的给定状态域,若存在正常数ν>0,ρ>1和正定矩阵Pi,Pj>0(i,j∈N,i≠j)使得 (41) Pi<ρPj (42) 且有 (43) (44) 则对于初始状态x0∈C1,式(13)的所有轨迹满足x(t)∈C2,∀t∈[0,Tf]. Boost升压电路的控制框图如图5所示. 图中,iL为流经电感的电流实际测量值;uC为电容两端的电压实际测量值;iref和uref分别为变换器的稳态电流值和稳态电压值. 基于数字计算机的控制器以一定的采样周期采集Boost变换器的电量参数,并将采集到的数据进行量化处理,基于量化后的处理数据计算控制律,通过数字驱动电路实施对Boost变换器的控制. 由于控制器检测信号和计算的延迟,控制器检测到电感电流值和电容电压值再计算控制律需要经过一定的时间,然后再发出指令 图5 Boost电路控制框图 信号控制晶体管的导通和截止,因此实际控制律所依赖的Boost变换器电路模型的切换和晶体管的开关动作之间存在一定的时间延迟,由此导致了异步切换现象的发生. 电路中各器件参数为:电感L=12 μH,电容C=180 μF,电阻R=6 Ω,输入电压E=12 V. 将式(10)和(11)写成标准切换系统式(13)的形式,则系统参数为 切换信号为 为了便于比较,分别利用同步切换控制方法(不考虑计算延迟)和异步切换控制方法(考虑计算延迟)设计Boost变换器的控制律. 从仿真图中可以看出,在0.9 ms内随着时间的推移,电压和电流值最终维持在平衡状态值附近. 然而,从电流和电压接近平衡态时的曲线可以看出,在平衡态附近,电流及电压均出现了高频振动现象,原因是所采用的控制方法假定计算机中控制律的计算所依赖的电路模型切换与实际的晶体管开关导通/截止动作是同步发生的. 由于实际系统中存在0.05 ms的控制器检测信号和计算延迟,计算机依赖当前电参量uC与iL所得到的控制律实际控制的是0.05 ms后的电路模型,这种不匹配使得电流与电压值在平衡点处发生了频率较高的振动. (a) 系统切换信号时序图 (b) 电流变化曲线图 (c) 电压变化曲线图 依据定理设计Boost电路的异步切换控制律,为便于比较,系统运行指标参数与同步切换控制律一致,设置为c1=1,c2=10,Tf=1 ms,控制器设计参数调整为ρ1=ρ2=1.005,ν-=0.01,ν+=1.02. 通过对式(28)进行计算,系统的平均驻留时间可取为τa=0.18 ms,根据平均驻留时间的取值为系统选择切换周期为0.18 ms的周期切换律,脉冲信号频率为17 kHz. 图7(a)给出了电路系统的切换与实际控制律切换信号的时序图,两者之间存在0.05 ms的时间延迟. 图7(b)和(c)分别给出了异步切换控制下电流和电压的变化曲线图. 对比同步切换控制方法和异步切换控制方法可以看出,异步切换控制的驻留时间长于同步切换下的驻留时间,这是由于计算机检测信号和控制律计算延迟的存在导致基于计算机实施的控制方法中电路模型的切换与实际的晶体管切换时间不一致,因此电路的切换频次不宜过高,系统需要在每个子系统中停留足够长的时间来稳定电参量. 虽然2种方法在过渡阶段电容输出电压均经过1次切换便达到了平衡态,但考虑在0.9 ms运行时间内异步切换所实施的控制方法的总切换次数为5,明显少于同步切换所实施的控制方法的总切换次数11,未出现高频振动的现象,控制性能更优. (a)系统及控制律切换信号时序图 (b) 电流变化曲线图 (c) 电压变化曲线图 1) 本文提出了一种有限时间异步切换控制方法来处理Boost开关变换器电路的稳定性问题,该方法依赖于驻留时间切换条件,并给出了驻留时间与系统运行状态界之间的定量关系. 为了确保系统稳定性,除了控制律的设计,占空比的计算时间与切换信号驻留时间之间的关系也通过研究予以确立. 2) 本文通过分析变换器电路结构的混杂模型,指出在Boost电路分析和设计时计算延迟效应是不可忽略的因素,所提出的基于时间切换的Boost变换器控制方法能够有效克服计算延迟给电路稳定性带来的影响. 3) 比较了应用同步切换和异步切换2种控制方法的效果,在0.9 ms运行时间内,电路系统的切换与实际控制律切换信号之间存在0.05 ms的时间延迟时,异步切换所实施的控制方法的总切换次数为5,少于同步切换所实施的切换控制的总切换次数11,且未出现高频振动的现象. 仿真结果表明异步切换控制方法能够有效抑制电路输出响应在平衡点附近的高频振动,所提出的有限时间异步控制方法在电路的被控电参量输出上具有良好的控制性能,对工程应用具有实际的指导意义.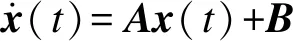
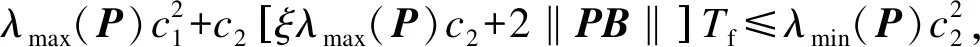







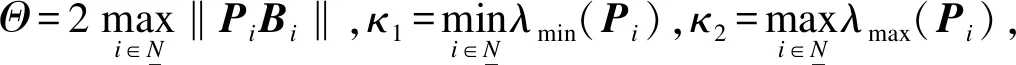
3 基于时间切换的Boost电路仿真


3.1 同步切换控制



3.2 异步切换控制


4 结 论
