斜心墙土石坝稳定—非稳定渗流分析与评价
2021-02-22宋昊
宋 昊
(上海市崇明区农村水利管理所,上海 202150)
1 引言
土质防渗斜心墙坝是我国20 世纪中期发展起来的一种土石坝坝型,随后在我国小浪底等土石坝中广泛采用这种坝型[1]。相比传统的心墙坝,土质防渗斜心墙坝具有坝坡稳定性强,上游防渗效果好等优点[2]。为评价土石坝的渗透性能,一般要进行稳定-非稳定渗流分析,进而对土石坝的渗透稳定性进行评估。通常相关学者的评价指标包括渗流量与出逸点渗透坡降。然而,传统土石坝渗流计算分析,一般主要针对均质土坝、心墙坝、混凝土面板堆石坝的渗流计算分析较多,对黏土斜心墙坝稳定—非稳定渗流研究报道较少[3]。因此,本文以某壤土斜心墙坝为工程背景,开展渗透稳定计算,基于计算指标来评价渗透稳定及渗漏损失是否满足安全要求。
2 工程概况
某水库为一灌溉、供水和防洪的综合利用水利枢纽工程,水库设计总库容为528 万m3。挡水建筑物由非过水土坝和过水土坝两坝段组成,3 级建筑物。设计标准为百年一遇洪水设计、千年一遇洪水校核。土坝全长163.5 m,其中过水土坝坝段位于河床部位,长72.0 m,溢流前沿净宽50.0 m。左右两岸为非过水土坝坝段,累计长度为91.5 m。最大坝高36.8 m。土坝防渗墙采用壤土斜心墙,上游侧边坡为1∶3,下游侧边坡1∶2.55。防渗斜墙顶部最小有效厚度为1.5 m,底部有效厚度为4.5 m。土坝坝壳由砂砾料填筑,壤土斜心墙上游侧砂砾料坝壳厚1.2 m,上游坝坡与壤土斜心墙上游侧边坡相同,为1∶3。下游侧砂砾料坝壳边坡非过水土坝坝段为1∶2,过水土坝坝段为1∶3。
3 计算分析方法
3.1 计算原理
(1)渗流计算原理
符合达西定律的二维非均质各向异性土体非稳定渗流的基本方程为:

稳定渗流的基本方程为:

式中:h为水头函数;x、y为计算坐标;t为时间;kx、ky为以x、y轴为主轴方向的渗透系数;为给水度。
式(1)~式(2)即为二向稳定和稳定渗流计算的基本微分方程和定解条件,联立求解即可确定土体的稳定渗流场和非稳定渗流场。
(2)渗流压力计算原理
根据渗流计算的流网可以得到水头损失的沿程变化,绘制出沿地下轮廓的渗流压力分布图。
(3)渗透坡降计算原理
根据《水利水电工程地质勘察规范》流土型的渗透变形的判别可采用以下方法:

式中:Jcr为土的临界水力比降;Gs为土粒比重;n为土的孔隙率。
设计时采用的容许水力比降等于临界水力比降除以安全系数:安全系数一般取1.5~2.0;当渗流稳定对水工建筑物的危害较大时,取2.0 的安全系数;对特别重要的工程也可用2.5 的安全系数。
3.2 计算模型
本论文中采用有限元法对大坝进行渗流计算,运用Geo-Stvdio软件中seep/w模块,建立大坝现状最大横断面的二维有限元模型。根据大坝现状最大横断面(桩号0+100)建立有限元模型,模型范围为:大坝向上游与下游各取40 m,建基面以下取40 m。采用四边形单元为主、辅以三角形单元来进行有限元网格剖分,共包括5321 个单元,5409 个节点,得到的有限元网格见图1。

图1 大坝渗流计算有限元网格划分
3.3 计算参数
坝壳砂砾料、坝基砂砾石、坝体防渗斜墙、防渗心墙、坝体反滤层、坝基片麻岩、回填碎石渣及堆石排水体等渗流计算材料参数见表1。

表1 坝体和坝基渗流计算参数表
3.4 计算工况
参考《碾压式土石坝设计规范》(SL 274-2001)规定,渗流计算应考虑运行中出现的不利工况条件,按稳定渗流考虑,并考虑以下渗流计算工况:
(1)正常蓄水位工况:上游正常蓄水位288.80 m,下游对应水位取248.00 m;
(2)设计洪水位工况:上游设计洪水位290.30 m,下游对应水位取248.00 m;
(3)校核洪水位工况:上游校核洪水位291.60 m,下游对应水位取248.00 m;
(4)水位骤降工况Ⅰ:上游水位按水位降落速度0.5 m/d由正常蓄水位288.80 m骤降至死水位265.00 m,下游对应水位取248.00 m;
(5)水位骤降工况Ⅱ:上游水位按水位降落速度1.0 m/d由正常蓄水位288.80 m骤降至死水位265.00 m,下游对应水位取248.00 m。
4 计算结果分析
本次正常蓄水位工况、设计洪水位工况及校核洪水位工况下渗流计算的渗透坡降、渗流量及坝体出逸点计算成果见表2,计算的浸润线位置及等势线图见图2~图4。由表2 及图2~图4 可以看出,在上下游水位差的作用下,渗流区域主要集中在斜心墙区域,没有出现明显的集中渗流。由于防渗墙的作用,坝体内部的浸润线大致沿着斜墙部位快速下降,坝后浸润线很低,正常蓄水位、设计洪水位和校核洪水位工况的坝体出逸点高程变化正常,随着上游水位的升高略有增大。同时,计算结果表明,随着上游水位增大,正常蓄水位工况、设计洪水位工况及校核洪水位工况下坝体渗流量分别为29.91 m3/(d·m)、30.05 m3/(d·m)、30.95 m3/(d·m),表现为逐渐增大的趋势。此外,坝体出逸段的渗透坡降也随着上下游的水位差逐渐增大,坝体出逸面是坝基片麻岩,故坝体出逸点渗透稳定。坝体及坝基与堆石排水体接触面的渗透坡降小于允许值,故坝体及坝基渗透稳定。

图2 正常蓄水位工况浸润线位置及等势线图
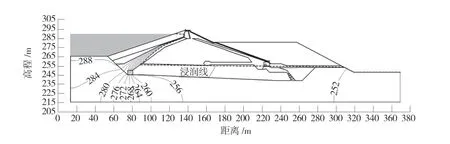
图3 设计洪水位工况浸润线位置及等势线图

图4 校核洪水位工况浸润线位置及等势线图
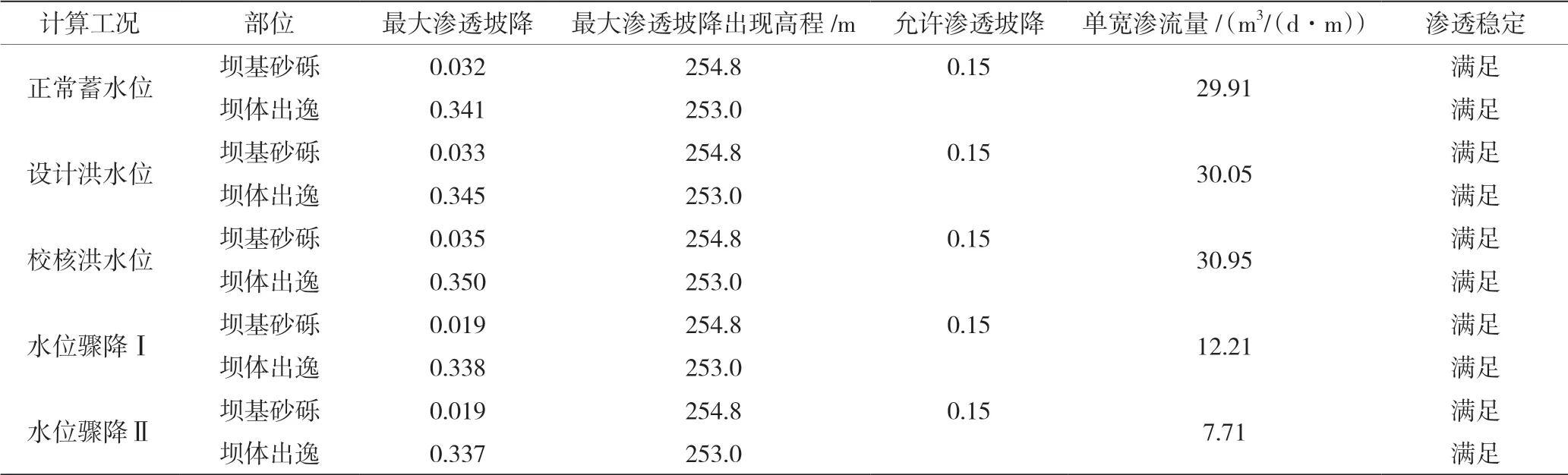
表2 各工况渗流分析结果
本次水位骤降工况Ⅰ、Ⅱ工况下渗流计算的渗透坡降、渗流量及坝体出逸点计算成果见表2,取计算时间段任意时刻的浸润线位置及等势线图见图5~图6。由表2及图5~图6可以看出:降落水位即为浸润线与上游坝坡交点的高程。不同时段上游坝体内的浸润线基本与水位降落速度同步,基本均呈现为“Z”字形斜线;相比较而言,水位骤降工况Ⅰ的上游坝体内浸润线高于水位骤降工况Ⅱ的浸润线,且随着降落水位的逐步降低,两者浸润线的高差相应增大。当降至死水位时,骤降工况Ⅰ和工况Ⅱ的浸润线相同。根据以上分析可以得出,随着上游水位降落速度由0.5 m/d增加至1.0 m/d,坝体渗流量减小36.8%,渗透坡降基本一致,均满足渗透稳定要求。

图5 水位骤降工况Ⅰ等势线及浸润线位置图
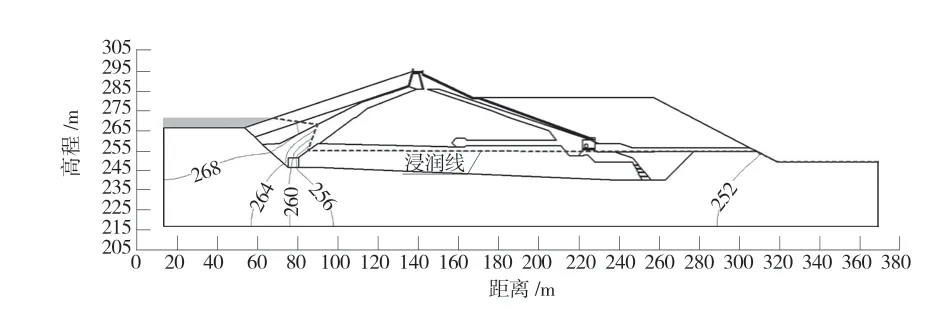
图6 水位骤降工况Ⅱ等势线及浸润线位置图
5 结论
(1)通过分析不同工况下的水头等值线、浸润线、渗流量等结果,发现正常蓄水位、设计洪水位及校核洪水位工况下随着上下游水头差的增大,渗流量与出逸点渗透坡降均有所增大。水位骤降工况下,随着上游水位降落速度增加,坝体渗流量增大,渗透坡降变化不大。
(2)由于斜墙坝坝体内部设置了壤土斜墙,有效地降低了浸润线,各工况下坝体浸润线和出逸点的位置正常,坝体满足渗透稳定要求。
