基于虚拟孔径扩展的稀疏嵌套阵设计

闫肃

(北京理工大学 信息与电子学院，北京 100081)

近年来稀疏阵列因其在减少阵元和增加自由度方面的优势而备受关注[1-2]. 通过对接收信号的协方差矩阵矢量化，能生成一个等效的差分共阵(difference co-array,DCA)，其自由度(degree of freedom,DOF)从O(N)增大到O(N2)[1]. 在虚拟阵列上使用子空间方法[2]或压缩感知方法[2]，可以检测到空间中的更多信源，获得更高的空间分辨率. 基于该方法，许多稀疏结构[1-6]及应用[7-10]相继被提出，其中最著名的是嵌套阵[1]和互质阵[2-3].

基于子阵的阵元间距和阵元数的互质性，提出的互质阵列[2-3]，被用来避免空间混叠，降低阵元间耦合，其自由度没有明显提升. 嵌套阵列(nested array,NA)[1]由N1+1个位于Sd={l|l∈[1,N1+1]}且阵元间距为1个单位的密集阵元，与N2个位于Ss={(N1+1)l|l∈[2,N2+1]}且相邻阵元间距为N1+1个单位的稀疏阵元组成. 其任意两阵元的位置差可以产生任意非负整数v=v1(N1+1)+v2，其中v1∈[0,N2]，v2∈[0,N1]. 因此，其DCA连续长度为N2(N1+1)+N1. 由于受到其无孔特性的限制，如果不扩展物理孔径，嵌套阵将无法获得更高自由度. 为解决这个问题，文献[7]提出的ANAI结构，将密集子阵分为两个子阵R11和R12(R11∪R12=Sd)，并把R12移到稀疏子阵的右侧. 因此，在[0,N2(N1+1)+N1]范围内的虚拟阵元仍然是连续的. 此外，由v=N2(N1+1)+v2(其中v2∈R11⊕R12)产生的额外虚拟段会使自由度增加. (符号⊕代表两个子阵的直和. )基于ANAI概念，进一步提出了改进的嵌套阵列(improved nested array,INA)[9]和ANAI-2[5]. 本文将这种中间具有稀疏均匀线阵(uniform linear array,ULA)且两侧具有两个稀疏非均匀线阵的嵌套阵列，称为三段式嵌套阵(3-segment nested arrays,3sNA). 此结构能有效地增大DOF. 但由于R11和R12中的最大元素不大于N1，其最大自由度不会超过(N1+1)N2+2N1-1. 为突破这一限制，需要放宽R11∪R12=Sd这个条件.

本文根据v=v1(N1+1)+v2=(v1-1)(N1+1)+(N1+1+v2)这种变形表示，提出了通过减少中间子阵传感器数目和扩大N1+1单侧子阵阵元间距来生成非负整数v，构造分布更加稀疏的嵌套阵列方法. 基于该方法，本文进一步提出一种新型稀疏结构——单侧稀疏嵌套阵(one-side sparse nested array,OS-SNA). 与最大阵元间距约束(maximum inter-element spacing constraint,MISC)[10]结构不同的是，OS-SNA的N1既可以是奇数也可以是偶数. 并且提供了更高的DOF和完整的结构解析表示.

1 差分共阵概念

(1)

(2)

DS=S-S={Δp=pi-pj|∀pi∈S,∀pj∈S}

在{Δp|Δp∈[-Lu,Lu]}处提取等效的ULA，其中Lu为自由度，并且在z中平滑相应的行，可获得虚拟单快拍

(3)

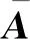
2 稀疏嵌套阵策略及OS-SNA结构

2.1 稀疏嵌套阵策略

定义一个整数ξ和集合A的加法：ξ±A={ξ±a|ξ∈Z,a∈A}. 为了后续研究方便，本文用相对位置代替物理位置表示稀疏阵.

定义1相对位置(relative position，RP) 对于中心子阵有N2个元素位于(N1+1)l,l∈[2,N2+1]的三段式嵌套阵，相对位置定义为

(4)

式中物理传感器的位置为S,其相对位置可以表示为{l,l∈S}.

注意0∈R11且0∈R12. 根据相对位置表达式，可以通过S={N1+1-r|r∈R11}∪{(N1+1)r|r∈[2,N2]}∪{(N1+1)(N2+1)+r|r∈R12}获得相应的传感器物理位置. 如图1所示，在一个N1=5，N2=3的ANAI-2结构中，物理传感器位于S={1,2,4,6,12,18,24,25,27},其相对位置为R11={0,2,4,5},R2={6,12,18},R12={0,1,3}.

(5)

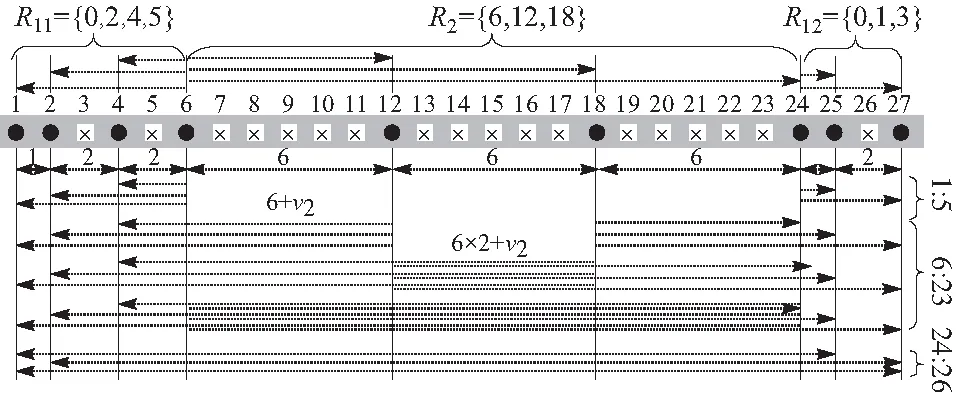
图1 N1=5和N2=3的ANAI-2结构的虚拟段和RP表示Fig.1 The RP representation and the virtual lags generation of ANAI-2 with N1=5 and N2=3

为了突破上述极限，一个可行方法是增大阵元的间距，增大R1和R2中的最大数. 但阵元的稀疏分布可能会造成差分共阵的不连续. 为了获得尽可能大的连续范围，本文提出了以下稀疏嵌套策略. 当v1∈[1,N2],v2∈[0,N1]时，将v=v1(N1+1)+v2重新写成v=(v1-1)(N1+1)+(v2+N1+1). 可以发现v3=v2+N1+1是v2的有效替代. 这说明可以在中间子阵放置较少的传感器和增加两侧子阵的离散度，在差分共阵中生成一个无孔的Vbody. 例如，对于N1=10的情况，数字12可以代替1获得整数11n+1，其中的n可以是从1开始增大的任一整数. 也就是说，如果在R11或R12中存在1，那么23可以由11×2+1表示；如果R11或R12中没有1，23也可以由11×1+12表示. 对于以上所述的稀疏嵌套阵的相关概念，只要在R[R11∪R12]N1+1中的余数能够包含的[0,N1]所有整数,虚拟段[N1+1,(N1+1)(N2+1)-1]就是连续的.R[N]m是{n/m|n∈N}的余数. 因此，大可不必将传感器放置得很密集，更广的稀疏度依然可以生成连续段.

2.2 单边稀疏嵌套阵结构

基于之前的策略，本文提供一种解析结构，该结构将右侧子阵元素从v2∈[0,N1]拓展到N1+1+v2∈[N1+1,2N1+1]，用以生成更长的连续范围.

定义2单边稀疏嵌套阵(one-side sparse nested array,OS-SNA)对正整数N1=2l，l≥5且N2≥1，OS-SNA由整数集合定义为

(6)

对N1=2l-1，l≥6的结构，整数集合具有下列形式：

(7)

该结构具有下列性质.

定理1对N1≥10的偶数，OS-SNA的自由度可以表示为Lu=(N1+1)N2+3N1-3. 对N1≥11的奇数，OS-SNA的自由度可以表示为Lu=(N1+1)N2+3N1-2.

证明

1) 考虑偶数N1=2l≥10，根据上述的相对位置表达式,可以推断：

②R[R11∪R12]N1+1={0,l∶2l-3,2l,1∶l-1,2l-2,2l-1}=[0,N1]；

③R11⨁R12={0,l,l+2∶2l-3,2l‖l+1,2l+1,2l+3∶3l-2,3l+1‖2l+2,3l+2,3l+4∶4l-1,4l+2‖2l+3,3l+3,3l+5∶4l,4l+3‖…‖3l,4l,4l+2∶5l-3,5l‖4l-1,5l-1,5l+1∶6l-4,6l-1‖4l,5l,5l+2∶6l-3,6l}⊃[2l+2,6l-3]=[N1+1,3N1-3].

所以,上述的相对位置表达式能够使正向差分共阵在[0,(N1+1)N2+3N1-3]范围内连续. 自由度Lu=(N1+1)N2+3N1-3.

2) 考虑奇数N1=2l-1≥11，则

②R[R11∪R12]N1+1={0,l-1,l+1,2l-3∶2l-1,1∶l-2,l,l+2∶2l-4}=[0,2l-1]=[0,N1].

③R11⨁R12={0,l+1,2l+1∶3l-2,3l,3l+2∶4l-4‖l-1,2l,3l∶4l-3,4l-1,4l+1∶5l-5‖2l-3,3l-2,4l-2∶5l-5,5l-3,5l-1∶6l-7‖2l-2,3l-1,4l-1∶5l-4,5l-2,5l∶6l-6‖2l-1,3l,4l∶5l-3,5l-1,5l+1∶6l-5}={0,l-1,l+1}∪[2l,6l-5]⊃[2l,6l-5]=[N1+1,3N1-2].

所以,上述相对位置表达式的OS-SNA结构能够使正向差分共阵在[0,(N1+1)N2+3N1-2]范围内连续. 自由度Lu=(N1+1)N2+3N1-2.

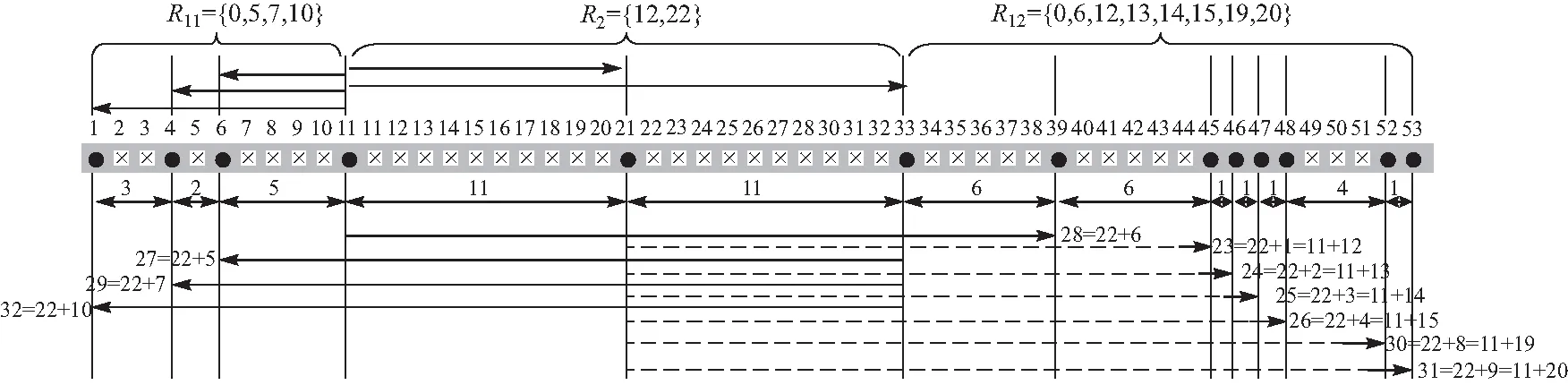
图2 N1=10，N2=2时的OS-SNA的结构示意Fig.2 The SNA concept illustrated by the proposed OS-SNA with N1=10 and N2=2

3 仿真实验

3.1 自由度

首先，将NA、ANAI-2、INA、MISC的自由度与提出的OS-SNA的自由度进行比较. 假设以上所有结构中有N2个元素位于(N1+1)l，l∈[2,N2+1] 的子阵中. 如表1所示，OS-SNA 的自由度是最大的，其次是MISC、INA、ANAI-2和NA. 对于MISC，在N1为偶数时表达式不存在. 对这几种不同的结构分别能达到的自由度上限来说，本文提出的策略在理想情况下有可能自由度达到(N1+1)N2+3N1. OS-SNA结构可以识别比上限少2～3个数量的信源. MISC实际上是SNC概念的框架，它满足定理1，但是自由度比OS-SNA低.

表1 不同的三段式嵌套阵的自由度比较

3.2 DOA估计

在NA、INA、ANAI-2、MISC、MRA和提出的OS-SNA 6种结构中，假设有D=23个不相关信源均匀入射在-30°～30°的区间内. 图3给出了这6种嵌套阵的单次DOA估计结果. 传感器数N=13,N1=11,N2=1.Smra={1,2,3,9,16,17,27,37,47,50,54,56,59}. 信噪比为10 dB. 蒙特卡洛次数K=2 000. 本文进行了200次蒙特卡洛试验. 可以看出，NA、INA、ANAI-2、MISC的MUSIC估测结果中，DOA估计是有明显错误的. 只有OS-SNA和MRA有着更高的自由度，能够得到正确的预测.

图3 6种结构的DOA估计Fig.3 DOA estimations for six kinds of nested arrays

然后，考虑了14个传感器11个信源的情况(N1=11,N2=2). 其他参数与上述实验相同. 图4(a)为在-15～20 dB的信噪比和快拍数为2 000下的均方根误差结果；图4(b)为固定信噪比为10 dB时的快拍数与均方根误差的变化. 如图4所示，OS-SNA比其他4种嵌套阵均方根误差更小且更接近MRA.

图4 均方差估计Fig.4 RMSEs

4 结 论

为了在三段式嵌套阵中扩展连续段的长度，本文提出了一种策略，该策略通过将中心子阵借出N1+1长度到两侧子阵来使阵形更加稀疏化. 在此基础上，本文提出了一种新的具有完整解析表达式的结构，该结构具有比现有嵌套阵列更高的自由度. 仿真结果验证了其有效性.