基于同一个情境开发课后作业的尝试
2021-02-21蔡钳陈信余
蔡钳 陈信余


摘 要:课后作业是左右学生学业负担是否过重的重要因素,也是广大教师、学者普遍关注的教学问题之一。文章尝试以学业质量水平为基础,创设一个真实情境,并基于此情境开发不同水平的作业,试图通过提高作业的质量和针对性减轻学生的学业负担,并促进不同层次学生的思维发展。
关键词:课后作业;分层作业;学业质量水平;真实情境;思维发展
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2021)1-0016-3
学业质量是《普通高中物理课程标准(2017年版)》[1](以下简称课标)中提到的一个重要内容,学业质量水平的划分为教学、考试命题和课后作业设计都提供了依据。其中提到:“创设真实而有价值的问题情境,采用主体多元、方法多样的评价方式,客观全面了解学生物理学科核心素养发展状况,找出存在的问题,明确发展方向,及时有效地反馈评价结果,促进学生全面而有个性地发展。”
课标对生产生活中的物理情境试题命制流程做了示范:(1)确定考核目标;(2)描述情境的各项任务;(3)根据考核目标和任务确定问题。
学生作业负担过重一直是教育界普遍关注却无法解决的问题。笔者所在的团队对这个问题也有过多年的研究,结合对学业质量水平内涵的理解和课标关于试题命制的做法,尝试在学完某一知识内容后,创设一个真实的情境,并基于同一个情境开发不同水平、适合不同思维层次学生的问题,并在评价方面进行“不仅仅拘泥于知识本身”的尝试。下面通过三个案例介绍这种做法。
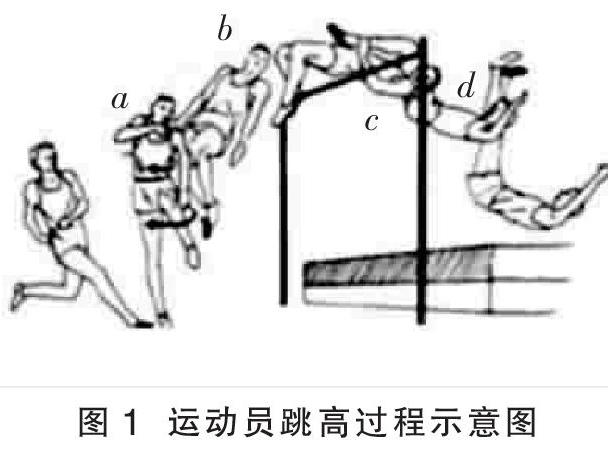
案例1 设计《牛顿第二定律》课后作业。创设真实情境:跳高运动员从蹬地起跳,到横跨过杆,最后落地的过程(图1)。
考核目标:考查对质点的认识、超重与失重的认识、作用力与反作用力的认识;应用牛顿第二定律、匀变速直线运动规律等解决问题的观念;考查科学思维中的分析、推理能力。
任务描述:(1)跳高运动员蹬地起跳,与地面相互作用,地面支持力大于重力;(2)跳高运动员斜向上运动,做减速运动,加速度向下;(3)跳高运动员下落,做加速运动,加速度向下;(4)跳高运动员在最高点的速度不为零。
水平1:下列可将运动员视为质点的是( )
A.研究运动员的跳高方式时
B.研究运动员的跳高成绩时
C.研究运动员跳离地面的转体动作时
D.研究运动员落在垫子上的部位时
该题考查学生对模型的基本认识,属于科学思维水平1的要求。
水平2:运动员在b、d位置的状态分别为( )
A.超重、超重 B.超重、失重
C.失重、失重 D.失重、超重
通过实验,认识超重和失重现象,了解所学的物理概念和规律,能解释自然现象,解决简单的实际问题。属于物理观念水平2的要求。
水平3:运动员在a处起跳瞬间( )
A.地面对人的作用力等于人对地面的作用力
B.地面对人的作用力大于人对地面的作用力
C.地面对人的作用力大于人的重力
D.人对地面的作用力等于人的重力
理解牛顿运动定律,能用牛顿运动定律解释生产生活中的有关现象、解决有关问题。并运用力与运动观念分析、推理、解决问题。属于物理观念、科学思维水平3的要求。
水平4:运动员在a处从开始蹬地到离地过程(视为匀加速),加速过程中重心上升的距离为“加速距离”。离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。某同学身高1.8 m,质量80 kg,在某次跳高比赛时“加速距离”为0.5 m,起跳后身体横着越过(背越式)2.15 m高的横杆。试估算人的起跳速度v和起跳过程中地面对人的平均作用力F(g取10 m/s2)。
理解牛顿运动定律,能用牛顿运动定律解释生产生活中的有关现象、解决有关问题;通过理论推导和实验,理解动量定理,能用其解释生产生活中的有关现象。能将实际问题中的对象和过程转换成所学的物理模型;能对综合性物理问题进行分析和推理,获得结论并作出解释。属于物理观念、科学思维水平4的要求。
水平5:运动员在a处开始蹬地,离地瞬间速度大小为v1,方向与水平方向夹角为θ。落地瞬间速度大小为v2,方向与水平方向夹角为α。已知运动员受到的阻力与速率成正比,假设落地点与起跳时重心高度相等,重力加速度为g,求运动员从离开地面到落地所经历的时间t。
能在受线性变化阻力这种新的情境中对问题进行分析和推理,应用微元法结合力与运动观念分析、解决问题。属于高中阶段的最高要求。
在一个情境中开发五个不同水平的作业题,让学生在有限的课余时间中进行思维进阶通關游戏,水平低的学生完成前3题,努力思考第4题;水平中上的学生完成前4题;水平极高的学生完成5道题。这样处理,既节省了时间,又再一次让学生经历知识建构、问题进阶的全过程,其优点不言而喻。
案例2 设计《平抛运动》课后作业。创设真实情境:沿水平方向匀速运动的飞机,每隔相同时间释放一颗炸弹(图2)。
考核目标:考查对平抛运动规律的理解,运用力与运动观念解决平抛运动问题的能力;考查运用平抛运动规律解决问题的观念;考查科学思维中应用物理规律对具体问题进行分析、推理的能力。
任务描述:(1)飞机每隔相同时间释放一颗炸弹,每颗炸弹做平抛运动;(2)炸弹的水平速度与飞机相同,因此落地前与飞机在同一竖直线;(3)炸弹运动过程中,相邻炸弹的距离越来越大,且呈现一定规律;(4)能运算炸弹投中各类目标的相关数据。
水平1:关于每颗炸弹离开飞机后,对其运动的描述正确的是( )
A.做自由落体运动
B.向下做匀速直线运动
C.做平抛运动
D.向下做匀加速直线运动
水平2:请解释炸弹落地前排出一条竖直线的原因。
水平3:在所有炸弹落地前,第n颗炸弹释放瞬间,下列分析正确的是( )
A.相邻炸弹之间的距离保持不变
B.相邻炸弹之间的距离越来越大
C.第n颗、n-1颗、n-2颗、n-3颗炸弹之间的距离的比是1:3:5
D.第1颗、2颗、3颗、4颗炸弹之间的距离的比是1:3:5
水平4:以初速度v0=100 m/s沿水平方向匀速运动的飞机A,每隔t=3 s时间释放一颗炸弹, 记最先释放的炸弹为第1颗,以后释放的炸弹依次是第2、3、4……已知当第1颗炸弹落地时速度与水平方向夹角与第6颗炸弹速度与竖直方向夹角相同,第3颗炸弹在某高度处垂直击中一飞机B的机身,被击中飞机的机身与水平方向夹角为30°,求:
(1)投弹飞机A所在的高度H;
(2)飞机B被击中时离第1颗炸弹落地点的水平距离。
案例2从水平1向水平4发展的设计与案例1相似,其作用不再赘述。下面通过案例3介绍在评价方面进行改进的做法。
案例3 创设情境:如图3所示,一个小球从半径R=0.8 m的光滑1/4竖直圆弧轨道底端滑入,小球的初速度v0=4 m/s,请选择一种你认为合适的方法求小球到达圆弧顶端的时间。
这是一个极简单的情境,却是一个不容易解决的问题,通过这样的问题,可以让学生尽最大努力“搜索”解题思路,嘗试解决问题。而对学生的答案,不该以简单的“对错”进行评价,还应该考虑学生答案所体现的思维层次。
层次三:将小球的运动分为两段,从开始运动到经过一半圆弧长时间为t1,剩下一半圆弧长运动时间为 t2,设小球到达轨道中点的速度为v1,由机械能守恒定律:
层次四:将小球的运动分为三段,从开始运动到经过三分之一圆弧长时间为t1,中间三分之一圆弧长运动时间为 t2,最后三分之一圆弧长运动时间为t3,设小球到达第一段三分之一圆弧末端的速度为v1,到达第二段三分之一圆弧末端的速度为v2,由机械能守恒定律:
(评价:将圆弧分段处理的思想,已经接近处理非线性问题的微积分思想,可给满分)
层次五:采用微积分严格求解。
如图4所示,小球从最低点以初速度v0滑入光滑圆弧后,小球运动的路程对应的圆心角为θ时,小球的速度为v=Rω=R■(角速度大小等于角度对时间的导数)
总结与反思:基于一个真实情境开发整节课(整章)作业不仅能够节约学生完成作业的时间,提高效率,还能够较好地落实学业目标要求。主要有三个优点:(1)能够让学生经历从低阶思维向高阶思维发展的全过程,有利于不同层次的学生通过作业得到不同层次的提高;(2)能够让学生经历理解物理规律到应用物理规律解决问题的全过程,较好地培养物理观念;(3)能够让学生经历从认识模型、模型建构到应用模型解决问题的全过程,较好地培养科学思维。
参考文献:
[1]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[2]廖伯琴.普通高中物理课程标准(2017年版)解读[M].北京:高等教育出版社,2018.
(栏目编辑 赵保钢)
