美国加州Ridgecrest地震的地震动特性分析

张琪 陈希 郑向远

摘   要：为研究同一地震序列中两场震源相近，发震时间间隔较短的主要地震活动中获取的地震动时频特性的异同，选取了2019年7月美国加州Ridgecrest地震序列中震级分别为MW 6.4和MW7.1的两场地震，对比研究了两次地震中地震动参数随着震中距的衰减趋势，并与俞言祥模型进行了对比;讨论了这两个相近事件中地震动三要素（峰值加速度、反应谱和持时）的异同，重点分析了两条不利地震动的反应谱;通过希尔伯特-黄变换（HHT）获得地震动的HHT谱，分析了地震动能量在时间和频率成分上的分布特征. 结果表明：大部分地震动参数的衰减趋势与俞言祥模型吻合较好;两场地震的反应谱基本相似;地震动HHT谱最大能量所对应的瞬时频率和地震动时程峰值加速度所在循环的峰-谷频率很接近;两次大地震相继发生可能会对结构造成更大的损坏.

关键词：地震序列;地震动特性;衰减关系;地震动三要素;希尔伯特-黄变换

中图分类号：P315.9                          文献标志码：A

文章编号：1674—2974（2021）01—0108—09

Abstract：In order to figure out the different temporal and spectral characteristics between two earthquakes with close hypocenter and short time interval in the same seismic sequence， two main shocks，MW 6.4 and MW 7.1 among the 2019 Ridgecrest earthquakes at California USA in July are selected. The attenuation trend of ground motions parameters with the change of epicentral distance for these two earthquakes is compared with Yu's model.  The difference of three key elements of ground motions between these two earthquakes，including peak ground acceleration， response spectrum and duration，are analyzed. The potential seismic damage to structures is discussed by the response spectrum analysis of the selected two severest ground motions. The Hilbert-Huang transform（HHT） is adopted to obtain the HHT spectrum of ground motions for identifying the energy distribution in temporal and spectral domains. It shows that the attenuation trend of most of data agrees with Yus model. The response spectra of the two earthquake events are similar. The instantaneous frequency corresponding to the largest energy of HHT spectrum is close to peak-trough frequency corresponding to the time series cycle with peak ground acceleration. Structures may be severely damaged subjected to two earthquakes occurred successively.

Key words：seismic sequence;ground motion characteristics;attenuation trend;three key elements of a seismic motion;Hilbert-Huang transform

基于地震動工程特性，选取适当的地震动进行结构物的动力响应分析，对于土木工程结构抗震设计和安全评估具有重要意义. 目前世界范围内各地震活跃国家或地区正逐渐建立起覆盖整个区域的强震观测台网，这些观测台网的布设为地震动研究提供了丰富的数据来源. 长期以来，地震动的研究主要集中在研究地震动三要素（峰值加速度、反应谱和持时）等时频域工程特性，以及基于地震动数据研究不同场地条件下的地震动衰减关系等.

近年来，基于实际地震动数据，冀昆等人[1]结合震害调查，对云南鲁甸MS 6.5地震从幅值特征、衰减关系等方面对地震动参数加以分析. 在此基础上，戴嘉伟等[2]将云南鲁甸MS 6.5和云南景谷MS 6.6地震进行对比，发现鲁甸地震地震动参数衰减快于景谷地震，该现象可能与Q值（介质品质因子）的区域差异性相关. 王恒知等[3]采用H/V单台谱比法分析了地震的场地放大效应，表明台站场地对地震动存在明显的放大现象. 夏坤等[4]对汶川地震部分台站记录进行分析，研究了传播距离和场地条件对远场地震动的影响. 国内外多年来涌现出与上述成果类似的研究[5-6]，不一一列出.

2019年7月4日和7月6日，在美国加州同一地点相隔不到34 h相继发生6.4级和7.1级强震，是一个较为特殊的事件. 这两次强震同属于一个地震断裂带，且震源相近，属于同一个地震序列. 因此，对这两个事件的地震动特征及其影响进行梳理和分析研究具有重要意义. 本文基于美国工程强震数据中心（CESMD）获取的地震动信息，首先对地震动衰减关系进行研究;其次，鉴于它们震源相近，本文还对比研究了两次地震动PGA、反应谱和持时等时频域特性的差异，并利用希尔伯特-黄变换研究了地震动能量在时-频域的分布特征.

1   数   据

1.1   地震信息

2019年7月4日10时33分，美国加利福尼亚州南部科恩县里奇克莱斯特（Ridgecrest）附近发生6.4级地震，震中位于瑟尔斯谷西南12 km处，震源深度10.7 km. 相隔不到34 h，该地区再次发生强震，震级达7.1级，震源深度8.0 km，震中与早前发生的6.4级地震震中十分接近，仅相距17 km. 虽然二者震级仅相差0.7级，但基本上不属于双震型事件. 目前一致的看法是，后者为主震，前者为前震[7]. 事实上，在二者之间还发生过一个5.4级前震.

这是加州近20年来破坏性最强的两次地震，均发生在长约45 km、宽约15 km的利特尔莱克断裂带上，震中附近地表出现大量裂痕及偏移，房屋倒塌，道路损毁，甚至引起火灾等次生灾害，造成1人死亡，数十人受伤，及超过50亿美元的较严重经济损失[8-9]. 图1[10]和图2[11]展示了由7.1级地震造成的地表开裂和房屋损坏情况. 同时，距离震中约300 km的洛杉矶和周边城市以及内华达州拉斯维加斯都有明显震感.

1.2   数据选取

本文中强震动记录数据来源于美国工程强震数据中心（CESMD）. CESMD自7月4日至7月11日，包括主震及次大地震（7.1级和6.4级）在内，共记录到105次地震（≥MW 3），剔除震源深度小于等于0（可认为是地面塌陷或人为引起的震动）的数据后，得到94次地震. 各地震震中分布如图3所示. 图4所示为各次地震震级随时间变化曲线，从图中可看出，在6.4级的次大地震和7.1级的主震之间发生的地震，震级主要集中在MW 3 ～ 4.5，余震震级主要集中在MW 4 ～ 5.5. 图5为地震震级与相应的震源深度分布散点图，从图中可知，震源深度主要集中于0～13 km，均属于浅源地震（震源深度小于70 km），因此对地面建筑物带来的破坏较为严重.

2   衰减关系

6.4级和7.1级地震震级均较大且相差仅0.7级，在同一地震序列中能量较接近，因此以这两次地震动记录为例，进行地震动参数衰减关系的讨论. 在给定震级、震中距等条件下，利用地震动参数的衰减曲线能够对地震动进行参数估计，从而用这些估计参数作为结构抗震和安全评估计算的输入[12-15].

鉴于这两次地震在加州的台站均有记录，本文分别选取了两次地震动中峰值加速度（PGA）和峰值速度（PGV）较大的地震动记录，7.1级地震中选取前49条水平地震动记录，6.4级地震中选取前34条水平地震动记录，并分别与已有模型对比. 该模型为俞言祥[16]基于美国西部NGA 强震数据库建立的基岩场地水平衰减关系模型，结果如图6所示.

从图6中可看出，对于7.1级和6.4级地震的PGA和PGV的实际记录值，俞言祥模型曲线基本从这些散点中间穿过. 这些记录数据能够较好地反映出PGA和PGV随震中距的增大而衰减的趋势. 其中，6.4级地震对应的PGA、PGV的残差平方和（SSR）均小于7.1级地震，如表1所示. 这说明该模型对6.4级地震的地震动参数预测更加准确. 此外，值得注意的是，在7.1级地震中，震中距R=34.5 km的台站CLC，其PGA和PGV均远远高于俞言祥模型的预测值，造成此差异的原因有二：1）台站CLC虽然震中距较大，但是其断层距Rrup = 2.8 km远远小于其余台站，说明该台站与发震断层十分接近，地震波传播路径较短，因而地震动参数较大;2）台站CLC所处场地条件为C类（软基岩），不满足俞言祥模型的基岩场地条件，可能存在较大程度的场地放大效应，因而地震动参数较大.

3   地震动三要素

为了研究该地震活动中地震动的时频域特性，本文从6.4级和7.1级两次较大地震中分别選择了137条和126条地震动记录，并按照震中距的大小分为<100 km，100～200 km以及>200 km三类（见表2），研究两次主要地震中震中距所造成的差异.

3.1   PGA和持时

表3给出了6.4级和7.1级地震中不同震中距下水平和竖向地震动峰值加速度（PGA）平均值，同时也给出了竖向和水平PGA的比值关系. 从表3中可看出在同一次地震中，随着震中距的扩大，无论是水平还是竖向地震动PGA都减小，这与PGA随震中距变化的一般规律相同[17]. 同时，竖向和水平PGA的比值PGAV /PGAH也随着震中距变大而减小. 对于不同震级（MW 6.4 vs. 7.1）同一震中距分类地震动而言，震级越大则PGA越大;另外，震级增大时，PGAV/PGAH也会增大.

表4列出了6.4和7.1级地震中不同震中距下水平和竖向地震动持时的平均值. 本文采用90%能量持时[18-20]来确定地震动持续时间（一般又称为强震持时），是由于这种方法能够更充分地反映地震动的原始特征. 该持时定义为地震动能量从总能量的5%累积到95%所经历的时间，见式（1）和式（2）.

式中：T为总持时，其分为3段，分别是0～T1，T1～T2和T2 ～ T，T1、T2分别是总能量的5%和95%所对应的时间点，Td表示90%能量持时. 从表4中可以看出，随着震中距增加，地震动加速度持时也相应增加，尤其在震中距大于200 km时，无论是水平向还是竖向地震动，加速度持时增幅最大. 另外，对于竖向和水平持时比值TV /TH，震中距在100 ～ 200 km内最大，震中距小于100 km最小. 值得注意的是，与PGA水平和竖向数值大小关系不同的是，对于地震动90%能量持时而言，竖向持时始终大于水平向持时. 不同的震级也会影响持时大小，在本地震事件中，震级大地震动持时也变大，但是TV /TH却略有减小.

3.2   反应谱

利用精确法计算地震动的5%阻尼比加速度反应谱[21-22]，并将所有反应谱归一化处理，计算每一类别的平均反应谱，从而对比研究其差异.

图7（a）（b）分别表示两次地震中不同震中距类别的水平和竖向地震动加速度反应谱，纵坐标β为归一化的加速度反应谱值. 从图中可看出，无论是水平还是竖向反应谱，对于同一次地震（6.4级或者7.1级），随着震中距增大，其谱值向长周期偏移，对于震中距超过200 km的地震动反应谱，其特征周期超过0.8 s，这反映出地震动传播距离越远，高频部分被削弱越多，而低频成分则不断扩大. 另外，对于同一震中距分类，不同震级的2条反应谱的差别较小，尤其是对应第一类和第二类震中距（皆小于200 km）的地震动. 造成如此结果的原因是这两次地震属于同一个地震序列，同时两次地震震源相近.

为了对比7.1级和6.4级地震中最显著反应谱的差别，本文选择了获取的所有地震动数据中7.1级地震PGA最大的地震动，以及对应于该地震动观测台站记录得到的6.4级地震的地震动数据，分别为R1和R2，具体信息见表5. 图8（a）（b）分别表示R1和R2的水平和竖向地震动反应谱（β为归一化的加速度反应谱值）. 对于水平方向的反应谱，在周期0.2 s < T < 0.5 s时，R1反应谱值显著大于R2，因此考虑到7.1级地震在6.4级之后发生，如果在此场地上的结构经受6.4级地震的地震动荷载后产生结构损伤，自振周期变长，在此情况下遭受7.1级地震，结构会受到更加严重的破坏. 此外，从竖直方向的反应谱也可看出，R1的反应谱峰值要大于R2.

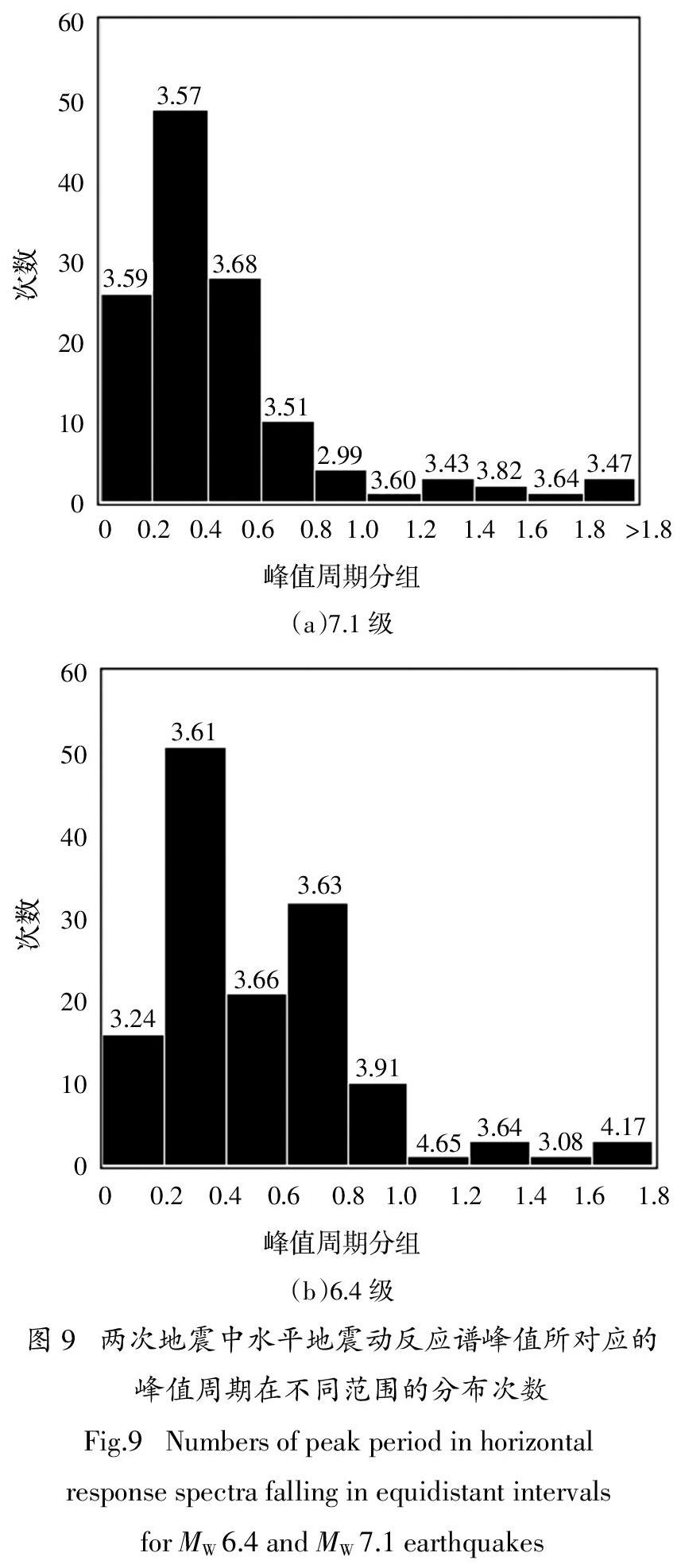
图9（a）（b）分别给出了7.1级和6.4级地震中水平地震动反应谱峰值所对应的周期（下称峰值周期）在不同范围的分布图. 除了图9（a）中最后一个柱形代表周期大于1.8 s的数据量，其他直方柱的周期间隔都是0.2 s. 直方柱的高度表示峰值周期落在某一周期范围内的地震动数量，直方柱顶端数据表示落在此周期范围内的各地震动反应谱峰值的平均值. 从图中可看出，无论是7.1级还是6.4级地震，两者大部分地震动峰值所对应的周期都落在0.2～0.4 Hz，在此周期内，7.1级地震的地震动平均反应谱峰值为3.75，比6.4级的平均反应谱峰值3.61略大. 另外两个差别是，对于6.4级地震，落在0.6～0.8 s范围内的地震动反应谱峰值个数超过30次，明显多于7.1级地震的地震动;对于7.1级地震的地震动，存在3条峰值周期大于1.8 s的较长周期地震动，而6.4级地震则没有.

4   HHT谱分析

4.1   希尔伯特-黄变换

针对地震动频域特征所采用的方法一般是傅里叶变换[23]，它更适用于平稳随机过程，即假设频率不随时间变化. 然而实际中地震动记录的幅值和频率成分不断随时间变化，在严格意义上是一个非平稳随机过程[24]，传统的傅里叶变换方法无法对地震动特性进行精细化研究. 为了较好地描述地震动从开始激发到强震段，然后衰减结束的全过程，本文采用希尔伯特-黄变换（HHT）[25-26]，研究地震动能量在时间和频率成分中的分布情况.

为了利用HHT谱对7.1级和6.4级地震动进行特征分析，本文从收集的地震动数据库中选择了2组数据进行研究. 每组中共2条地震动，其中第一组中一条是7.1级地震中记录到的最大水平地震动，该条地震动由“China Lake”地震台站记录得到，编号记为R1，另一条是该强震观测台站所获取的6.4级地震的水平地震动，编号记为R2，该组数据可以用来对比不同震级对地震动造成的影响差异. 由于该组地震动是两次地震中分别记录的最大和次最大地震动，研究它们的差异是很有意义的. 第二组是为了对比不同场地条件地震动HHT谱的差异，包含了7.1级和6.4级地震中不同台站获取的水平地震动数据，它们对应的震中距分别是116.3 km和115.4 km，十分接近，编号分别记为R3和R4，具体信息见表5.

4.2   HHT谱

4.2.1   第一组

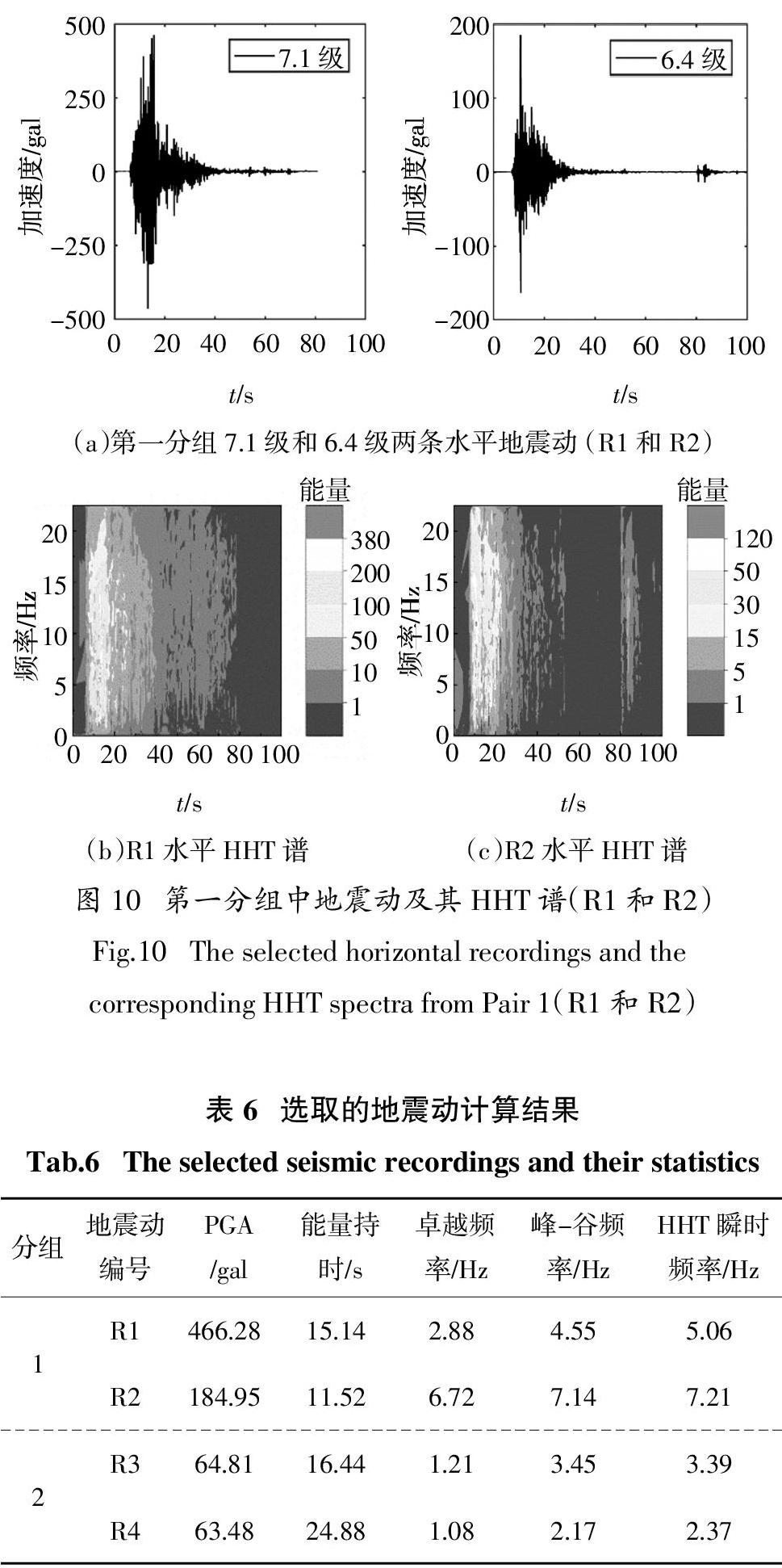
图10（a）分别给出了第一组中7.1级和6.4级地震中记录的两条地震动R1和R2的时程和HHT谱. 由于这两条地震动都是从同一个强震观测台站获取的，因此它们所在的场地条件是相同的，属于B类场地，不同的是震级以及震中距的差别. 从图中可看出，R1的PGA为466.28 gal，而R2的为184.95 gal，这主要是因为R1的震级比R2的震级大所致，而且震中距明显偏小. 另外，R1的能量持时也比R2的大，分别是15.14 s和11.52 s.

图10（b）（c）反映了R1和R2的能量在时间和频率上的分布情况. 其中，R1的HHT谱中显示最大瞬时能量为442.7 gal2，所对应的瞬时频率为5.06 Hz，发生在地震动时程的第15.6 s. R2的HHT谱中最大瞬时能量为209.2 gal2，比R1最大瞬時能量小很多，这也体现在两者的PGA的大小上，其所对应的瞬时频率为7.21 Hz，大于R1的瞬时频率. 由此可见，该台站所记录的7.1级地震的地震动与6.4级地震动相比，主要能量偏向于更低频成分. 考虑到7.1级地震在6.4级之后，这会对结构造成更严重的破坏，这与针对它们反应谱的分析结果一致.

由于通常情况下针对地震动特性的讨论是利用传统傅里叶变换进行频域分析，本文同样用该方法计算了地震动的卓越频率，即地震动功率谱中最大谱值对应的频率. 另外，进一步在时程上计算了各地震动PGA所在那个循环的峰-谷频率，具体结果见表6. 从表6中可看出，卓越频率是三者中最低的，而峰-谷频率更接近于HHT瞬时频率.

4.2.2   第二组

图11（a）给出了第二组中7.1级和6.4级地震中记录的两条地震动R3和R4的时程和HHT谱. 这两条地震动对应的震中距分别为116.3 km和115.4 km，基本一致，而强震观测台站所在场地分类不同，分别是D类和C类场地. 从图中可看出，R3的PGA为64.81 gal，R4为63.48 gal，两者的PGA基本相同，但是考虑到R3和R4的震级不同，一般来说，震级越大则PGA越大，如第一组地震动数据一样，但是这一组地震动PGA却十分接近，主要原因在于其场地条件的差异.

图11（b）（c）是R3和R4的HHT谱. 其中，R3的HHT谱中显示最大瞬时能量为62.36 gal2，所对应的瞬时频率为3.39 Hz，而R3的卓越频率为1.21 Hz，峰-谷频率为3.45 Hz，故而与第一组数据类似，峰-谷频率和HHT譜中最大能量对应的瞬时频率更加接近，而卓越频率是三者中最小的. R4的HHT谱中最大瞬时能量为55.28 gal2，略小于R3，与PGA的大小关系一致，其所对应的瞬时频率为2.37 Hz，小于R1的瞬时频率. 其卓越频率、峰-谷频率和HHT谱瞬时频率的关系与R3一致，见表6.

5   结   论

近期美国加州Ridgecrest发生的较大地震中，同一地震序列中存在6.4级和7.1级两次较大震级的地震活动，且两者的发生时间及震源较接近，本文分别收集了二者的地震动记录，研究它们相应的地震动特性，得到以下主要结论：

1）两场地震中所选地震动的PGA、PGV的衰减趋势与俞言祥模型吻合较好，其中6.4级地震的地震动参数与模型的吻合度更高. PGA和PGV大致随震中距的增大而衰减，但是断层距和场地条件的差异也可能造成PGA和PGV数值的异常. 另外，地震动的能量持时随震中距和震级的增大而增大，同一观测台站记录的竖向地震动能量持时大于水平向持时. 对于同一次地震，随着震中距增大，其反应谱值向长周期偏移. 同一地震序列中的两次地震（如本文6.4级和7.1级），它们的反应谱基本相似，尤其是在震中距小于200 km的情况下.

2）HHT变换可以获得地震动的HHT谱，从而用来分析地震动能量在时间和频率上的分布情况. 从频率成分来看，地震动HHT谱最大能量所对应的瞬时频率和地震动时程PGA所在循环的峰-谷频率很接近，卓越频率明显小于HHT瞬时频率和峰-谷频率. 由于两次地震的震中和发震时间比较接近，因此两次地震中地震动的时-频特性基本相似. 但也注意到，二者存在着差异，比如在震中的相同场地条件下，7.1级地震中所测记录（R1）的卓越频率和HHT瞬时频率都明显小于6.4级地震的记录（R2），因而对所处区域内的结构的动力响应自然也造成不同程度的影响.

3）通过对上述地震动分析可知，结构若经历6.4级地震之后产生损伤，其自振周期会变长，如果再次遭受主要能量更偏向长周期成分的7.1级地震的地震动作用，就可能会对结构造成更为严重的破坏. 这将通过后续的具体震害调查予以进一步确认和深入分析.

参考文献

[1]    冀昆，温瑞智，崔建文，等. 鲁甸 MS 6.5级地震强震动记录及震害分析[J]. 震灾防御技术，2014，9（3）：325—339.

JI K，WEN R Z，CUI J W，et al. Observation of strong motion and damage investigation for MS  6.5 Ludian earthquake[J]. Technology for Earthquake Disaster Prevention， 2014， 9（3）： 325—339. （In

Chinese）

[2]    戴嘉伟，冀昆，温瑞智，等. 云南景谷 MS  6.6级地震地震动特征分析[J]. 地震工程学报，2015，37（4）：969—975.

DAI J W，JI K，WEN R Z，et al. Ground motion characteristics of the Jinggu MS 6.6 earthquake in Yunnan[J]. China Earthquake Engineering Journal，2015，37（4）：969—975. （In Chinese）

[3]    王恒知，俞言祥，何斌，等. 高邮-宝应4.9级地震地面运动特征分析[J]. 地震地质，2018，40（6）：1349—1361.

WANG H Z，YU Y X，HE B，et al. Ground motion characteristics of Gaoyou-Baoying M4.9 earthquake[J]. Seismology and Geology，2018，40（6）：1349—1361. （In Chinese）

[4]    夏坤，张令心，董林. 汶川地震黄土地区远场地震动特征分析[J]. 防灾减灾工程学报，2018，38（1）：178—184.

XIA K，ZHANG L X，DONG L. Far-field ground motion characteristics of loess area in Wenchuan earthquake[J]. Journal of Disaster Prevention and Mitigation Engineering，2018，38（1）：178—184. （In Chinese）

[5]    汪梦甫，汪帜辉，唐毅. 近场脉冲型地震对结构非弹性位移比谱的影响[J]. 湖南大学学报（自然科学版），2014，41（6）：9—15.

WANG M F，WANG Z H，TANG Y. Influence of near-fault pulse-type ground motions on inelastic displacement ratio spectra[J]. Journal of Hunan University （Natural Sciences），2014，41（6）：9—15. （In Chinese）

[6]    潘毅，王忠凯，时胜杰，等. 尼泊尔8.1级地震加德满都-樟木沿线民居震害调查与分析[J]. 湖南大学学报（自然科学版），2017，44（3）：35—44.

PAN Y，WANG Z K，SHI S J，et al.Investigation and analysis on seismic damage of residential buildings along the highway from Kathmandu to Zhangmu in MS  8.1 Gorkha earthquake[J].Journal of Hunan University （Natural Sciences），2017，44（3）：35—44.（In Chinese）

[7]    ANSS. M7. 1- 2019 Ridgecrest earthquake sequence [EB/OL]. （2019-07-06） [2019-09-05].https：//earthquake.usgs.gov/earthquakes/eventpage/ci38457511/executive/.

[8]    ERIKA M，ERIC S. 1st fatality in Ridgecrest earthquake may be man found dead under jeep 100 miles from epicenter：investigators[EB/OL]. （2019-07-09）[2019-09-05].https：//ktla.com/2019/07/09/1st-fatality-in- ridgecrest -earthquake-may-be-man-found-dead-under-jeep-100-miles-from-epicenter-investigators/.https：//ktla.com/2019/07/09/1st-fatality-in-ridgecrest-earthquake-may-be-man-found-dead-under-jeep-100-miles-from-epicenter-investigators/

[9]    Los Angeles Times. Ridgecrest quake damage estimated above $5 billion at massive China Lake naval base [EB/OL]. （2019-08-14） [2019-09-05]. https：//ktla.com/2019/08/14/ridgecrest-earthquakes-left-up- to-5- billion-in-damage-to-massive-china-lake-naval-base/.

[10]  USGS. Update：magnitude 7.1 earthquake in Southern California [EB/OL]. （2019-07-06）[2019-09-05]. https：//www.usgs.gov/news/update- magnitude-71-earthquake-southern-california？qt-news_science_products=7#qt-news_science_products.

[11]  JESSICA M. California suffers earthquake damage，rockslides [EB/OL]. （2019-07-06）[2019-09-05]. https：//heavy.com/news/2019/07/ trona-earthquake-damage-photos/.https：//heavy.com/news/2019/07/trona-earthquake-damage-photos/.

[12]  陳鲲，俞言祥，高孟潭，等. 利用强震记录校正的芦山7.0级地震峰值加速度震动图[J]. 地震地质，2013，35（3）：627—633.

CHEN K，YU Y X，GAO M T，et al. Shakemap of peak ground acceleration with bias correction for the Lushan，Sichuan earthquake on April 20，2013 [J]. Seismology and Geology，2013，35（3）：627—633. （In Chinese）

[13]  LIU K S，TSAI Y B. Attenuation relationships of peak ground acceleration and velocity for crustal earthquakes in Taiwan [J]. Bulletin of the Seismological Society of America，2005，95（3）：1045—1058.

[14]  SADIGH K，CHANG C Y，EGAN J，et al. Attenuation relationships for shallow crustal earthquakes based on California strong motion data[J]. Seismological research letters，1997，68（1）：180—189.

[15]  YOUNGS R，CHIOU S J，SILVA W，et al. Strong ground motion attenuation relationships for subduction zone earthquakes[J]. Seismological Research Letters，1997，68（1）：58—73.

[16]  俞言祥，汪素云. 中国东部和西部地区水平向基岩加速度反应谱衰减关系[J]. 震灾防御技术，2006，1（3）：206—217.

YU Y X，WANG S Y. Attenuation relations for horizontal peak ground acceleration and response spectrum in eastern and western China[J]. Technology for Earthquake Disaster Prevention，2006，1（3）：206—217. （In Chinese）

[17]  张皎. 场地条件对地震动峰值及衰减关系的影响研究[D]. 北京：北京工业大学建筑工程学院，2008：17—23.

ZHANG J. Study on the effect of site condition to ground motion amplitude and attenuation relations [D]. Beijing：College of Architecture and Civil Engineering of BJUT，2008：17—23. （In Chinese）

[18]  白玉柱，徐锡伟. 由强震动数据分析芦山地震地面运动持时及周期特征[J]. 地震地质，2017，39（1）：92—103.

BAI Y Z，XU X W. Analysis on the characteristics of duration and period of ground motion of the Lushan earthquake based on the station records[J]. Seismology and Geology，2017，39（1）：92—103. （In Chinese）

[19]  潘志宏，洪博. 地震動频谱特性和持时对IDA结果影响的研究[J]. 振动与冲击，2014，33（5）：155—159.

PAN Z H，HONG B. Influence of spectral characteristics and duration of ground motions on results of IDA[J]. Journal of Vibration and Shock，2014，33（5）：155—159. （In Chinese）

[20]  TRIFUNAC M D，BRADY A G. A study on the duration of strong earthquake ground motion [J]. Bulletin of the Seismological Society of America，1975，65（3）：581—626.

[21]  BIOT M A. A mechanical analyzer for the prediction of earthquake stresses [J]. Bulletin of the Seismological Society of America，1941，31（2）：151—171.

[22]  NIGAM N C，JENNINGS P C. Calculation of response spectra from strong-motion earthquake records [J]. Bulletin of the Seismological Society of America，1969，59（2）：909—922.

[23]  BRACEWELL R N. The Fourier transform and its applications[M]. New York：Mcgraw-Hill Book Compay，1986：6—7.

[24]  欧进萍，牛荻涛，杜修力. 设计用随机地震动的模型及其参数确定[J]. 地震工程与工程振动，1991，11（3）：45—54.

OU J P，NIU D T，DU X L. Random earthquake ground motion model and parameter deternation used in a seismic design[J]. Earthquake Engineering and Engineering Vibration，1991，11（3）：45—54. （In Chinese）

[25]  HUANG N E，SHEN Z，LONG S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A：Mathematical，Physical and Engineering Sciences，1998，454（1971）：903—995.

[26]  HUANG N E. A new spectral representation of earthquake data：Hilbert spectral analysis of station TCU129，Chi-chi，Taiwan，21 September 1999[J]. Bulletin of the Seismological Society of America，2004，91（5）：1310—1338.