饱和土中非完全黏结管桩纵向振动特性研究

官文杰 吴文兵 蒋国盛 梁荣柱 刘浩

摘   要：基于Biot動力固结方程和Kelvin模型，考虑了土体三维波动效应及土塞与管桩之间的小变形相对滑移，研究了饱和土中非完全黏结管桩的纵向振动特性. 首先，引入势函数，结合桩侧土及土塞的初始和边界条件，采用Laplace变换技术、Helmholtz分解法及分离变量法，分别求解出桩侧土和土塞的纵向振动解. 结合桩土系统的耦合条件，进一步求解出管桩顶部的复刚度、速度响应频域解析解及速度响应时域半解析解. 将本文解分别退化为实心桩解和无相对滑移解，并与已有研究进行对比，验证了本文解的合理性. 然后，采用参数分析法初步确定了Kelvin模型参数的合理取值区间. 最后，分别分析了管桩桩长和土塞的渗透系数、孔隙率、剪切模量以及黏性阻尼系数对饱和土中非完全黏结管桩纵向振动特性的影响规律. 研究结果表明，桩长越短，土塞与管桩之间的黏结程度对饱和土中非完全黏结管桩纵向振动特性的影响越明显;土塞的孔隙率和黏性阻尼系数对饱和土中非完全黏结管桩的纵向振动特性有明显影响，土塞的剪切模量和渗透系数对饱和土中非完全黏结管桩的纵向振动特性的影响较小，可以忽略不计.

关键词：饱和土;端承管桩;Biot动力固结方程;Kelvin模型;相对滑移

中图分类号：TU 473                               文献标志码：A

文章编号：1674—2974（2021）01—0046—13

Abstract：Based on the Biot dynamic consolidation equation and the Kelvin model， the vertical vibration characteristics of the incompletely bonded pipe pile in saturated soil are investigated by considering the three dimensional effect of soil and the relative slip between the soil plug and pipe pile. Firstly， by introducing the potential functions and combining with the initial conditions and boundary conditions of the pile surrounding soil and soil plug， the vertical vibration solutions of the pile surrounding soil and soil plug are obtained by the Laplace transform method， Helmholtz decomposition method and separation variable method， respectively. Then， combining with the coupling conditions of pile-soil system， the complex stiffness， the frequency domain solution of the velocity and the semi-analytical solution of the velocity in the time domain of pipe pile top are obtained. Next， the degenerate solutions of this paper are compared with the corresponding existing solution to verify the rationality of the solution of this paper. Similarly， a parametric sensitivity analysis of the Kelvin model is conducted to preliminarily obtain the suitable values of the parameters of Kelvin model. Finally， the influence of the length of pipe pile， the permeability coefficient， porosity， shear modulus and viscous damping coefficient of soil plug on the vertical vibration characteristics of the incompletely bonded pipe pile in saturated soil are studied. The results show that， the shorter length of pipe pile leads to more obvious influence of the degree of bond between the soil plug and pipe pile on the vertical vibration characteristics of pipe pile in the saturated soil. The porosity and viscous damping coefficient of the soil plug have obvious influence on the vertical vibration characteristics of incompletely bonded pipe pile in saturated soil， and the influence of shear modulus and permeability coefficient of soil plug are too small to be neglected.

Key words：saturated soil;end-bearing pipe pile;Biot dynamic consolidation equation;Kelvin model;relative slippage

基桩动力特性一直是工程界的热点问题之一[1-2].随着我国海洋强国战略的推行，各类大直径管桩凭各自的特点和优点而被广泛应用于高桩码头、海洋平台、跨海桥梁、风电机组、输电塔等海洋工程中. 在大直径开口管桩沉桩过程中，管桩内部会形成土塞， 与桩侧土相比，土塞由于受到管桩内壁的约束，使土塞与管桩内壁间的相互作用更加复杂. 国内学者针对大直径管桩的静动力特性展开了大量的研究，刘汉龙等[3-4]提出了振动沉模现浇混凝土管桩 （Large Diameter Pipe Pile by using Cast-in-place Concrete，PCC）技术，并对其静动特性展开了一系列的理论及模型试验研究[5-6]. 基于刘汉龙等的研究，费康等[7-8]对PCC桩的单桩承载性能、荷载传递机理及其在低应变检测中的三维效应等问题进行了研究. Ding等[9-10]针对低应变检测法在PCC桩中的适用性和管桩的纵向振动特性等问题进行了研究. Zheng等[11-12]研究了不同土体本构模型下管桩的纵向及水平振动特性. 吴文兵等[13-17]考虑了土塞质量的影响及土塞与管桩之间位移的相位差，提出了附加质量模型来模拟土塞与管桩之间的动力相互作用，采用模型试验对该理论模型进行了验证，并系统研究了管桩的纵向及扭转振动特性，研究表明单相介质中管桩与土塞之间存在相对位移差的假设具有合理性.

但上述研究均将土体视为单相介质，在海洋工程中，土体处于完全饱和，不能简单地假设为单相介质，而是由固相-液相组成的两相介质. 刘林超等[18]结合饱和多孔介质理论与平面应变模型，研究了成层饱和土中管桩的纵向振动特性;郑长杰等[19]基于Biot动力固结方程，研究了饱和土中管桩的水平振动特性;靳建明等[20]基于Biot动力固结方程，研究了饱和土中管桩的扭转振动特性;Zheng等[21]研究了土体的横观各向同性对饱和土中管桩的扭转振动特性影响规律. 以上关于饱和土体中管桩动力特性的研究均假设桩侧土和土塞与管桩之间完全接触，无相对滑移. 然而，当管桩沉桩时土塞呈完全闭塞状态，土塞与管桩黏结程度极强，此假设符合工程实际，但当管桩沉桩时土塞呈非完全闭塞状态，此假设实际上夸大了管桩与土塞之间的相互作用. 与桩侧土体相比，土塞的质量较小，当管桩沉桩时土塞呈非完全闭塞状态，在动力作用下，土塞与管桩的接触面之间更容易产生相对滑移，且与单相介质土相比，由于水的存在，也更易使土塞与管桩之间产生小变形相对滑移. 因此，在研究饱和土中管桩动力特性时，考虑土塞与管桩之间的相对滑移显得十分必要. 本文基于Biot动力固结方程，考虑土体三维波动效应，采用与频率无关的Kelvin模型模拟土塞与管桩之间的相对滑移，研究了饱和土中非完全黏结管桩的纵向振动特性.

1   计算模型及基本假设

饱和土中非完全黏结管桩的纵向振动特性研究模型简图如图1 所示. 管桩桩长为H，外、内半径分别为r1、r2，管桩顶部作用有任意激振荷载p（t）;采用线性弹簧和线性阻尼器并联组成的Kelvin模型来模拟土塞与管桩之间的相对滑移，动刚度系数和动阻尼系数分别用kf和cf表示.

桩土振动系统满足如下基本假设：

1）桩侧土和土塞均为均质、各向同性的两相饱和介质，管桩底部为刚性支撑.

2）桩土系统纵向耦合振动为小变形，管桩外壁与桩侧土完全接触;采用Kelvin模型来模拟土塞与管桩之间存在的小变形相对滑移.

3）管桩为一维、弹性、圆环形均质杆件.

2   桩土系统控制方程的建立

2.1   土体振动方程及求解

根据Biot提出的饱和土动力固结方程，轴对称条件下土体的纵向振动方程可表示为：

4   Kelvin模型参数分析

根据Randolph等[25]提出的桩侧土动态Winkler模型经验公式：kf = 2.75G/2πr，cf = G/Vs，结合土塞的基本参数可得：kf = 1.46 × 107 N·m-3，cf = 1.40 × 105  N·m-3·s. 基于附加质量模型，Wu等[14]通过模型桩试验，反演出管桩纵向振动时附加质量模型中的Voigt模型参数的取值：kf = 7.85 × 105 N·m-3，cf = 1.53 × 105 N·m-3·s. 土塞受到管樁内壁的约束，其边界条件与桩侧土边界条件不同，因此连接土塞与管桩的Kelvin模型参数值不能仅根据Randolph等[25]提出Winkler模型经验公式选取. 已有研究表明，桩土相互作用阻尼系数在饱和土中的取值小于单相介质中的取值[26]，因此本文中Kelvin模型参数也不能仅参照Wu等[14]研究取值. 综上分析，Kelvin模型动刚度和动阻尼系数的上限值可初步设置为：kf = 1.46×107 N·m-3，cf = 1.53 × 105 N·m-3·s.

首先，分析动刚度系数kf对饱和土中管桩纵向振动特性的影响. 动阻尼系数cf = 0，动刚度系数kf分别设置为1 × 102、1 × 104、1 × 106、1 × 107、1.46 × 107 N·m-3. 由图5可知，当kf ≤ 1.46 × 107 N·m-3时，随着动刚度系数的增大，管桩顶部动刚度、动阻尼、速度频域及时域曲线均基本一致. 以上现象表明，动刚度系数在该区间内变化时，kf对管桩纵向振动特性的影响可以忽略. 因此，后续分析中，动刚度系数参照Wu等[14]研究取值：kf = 7.85×105 N·m-3.

接下来，分析Kelvin模型中动阻尼系数cf对饱和土中管桩纵向振动特性的影响. 动阻尼系数cf分别设置为1 × 102、1 × 103、1 × 104、1 × 105、1.53 × 105 N·m-3·s. 由图6可知，当cf ≤ 1 × 103 N·m-3·s时，随着动阻尼系数的增大，管桩顶部动刚度、动阻尼、速度频域及时域曲线均基本不变. 以上现象可能是由于动阻尼系数较小时，土塞与管桩之间的黏结程度较弱，土塞和管桩之间产生较大的相对位移，土塞性质对管桩纵向振动特性的影响较小. 同时通过大量试算，验证了动阻尼系数较小时，土塞性质对管桩纵向振动特性的影响可以忽略. 鉴于本文研究基于小变形假设展开，因此，下文中对于cf≤1 × 103 N·m-3·s的工况不再进行深入研究.

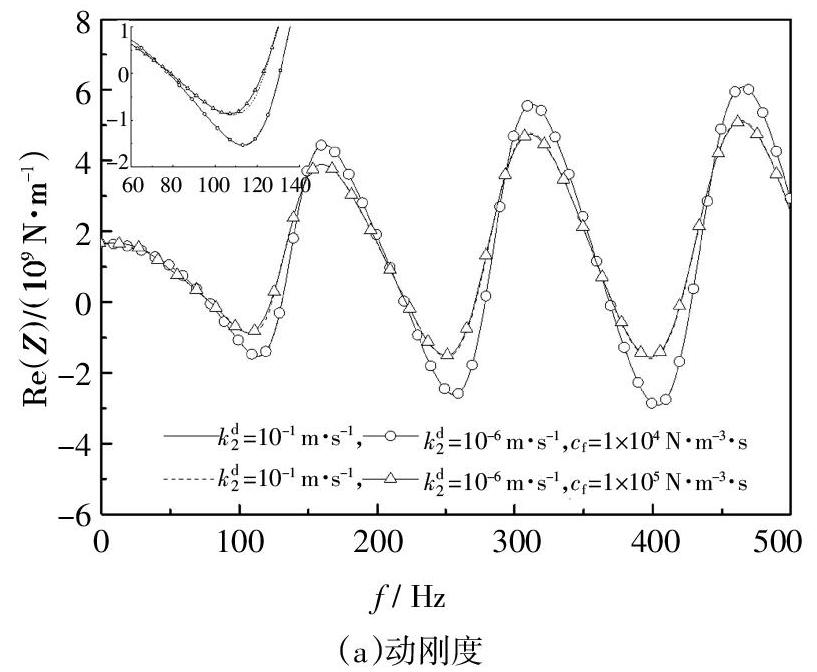
同时，由图6可知，当Kelvin模型中动阻尼系数cf在1 × 103 ～ 1.53 × 105 N·m-3·s变化时，随着动阻尼系数的增大，管桩顶部动刚度、动阻尼、速度频域曲线的振荡幅值均逐渐减小;速度时域曲线中桩底反射信号幅值逐渐减小. 以上现象可能是由于动阻尼系数cf在1 × 103 ～ 1.53 × 105 N·m-3·s变化时，动阻尼系数越大，即土塞与管桩之间的黏结程度较强，管桩与土塞之间的相对滑移较小，因此，土塞对管桩振动能量的耗散能力越强. 以上现象表明，动阻尼系数cf是影响管桩纵向振动特性的重要因素. 结合前文中初步确定的Kelvin模型参数的上限值，cf的取值区间可进一步缩小为：cf = 1×103～1.53 × 105 N·m-3·s.

综合上述分析可知，Kelvin模型中动阻尼系数对管桩纵向振动特性有明显影响，动刚度系数的影响较小，因此，在后续分析中单独用Kelvin模型中的动阻尼系数描述土塞与管桩之间的黏结程度.

5   参数分析

5.1   桩长影响分析

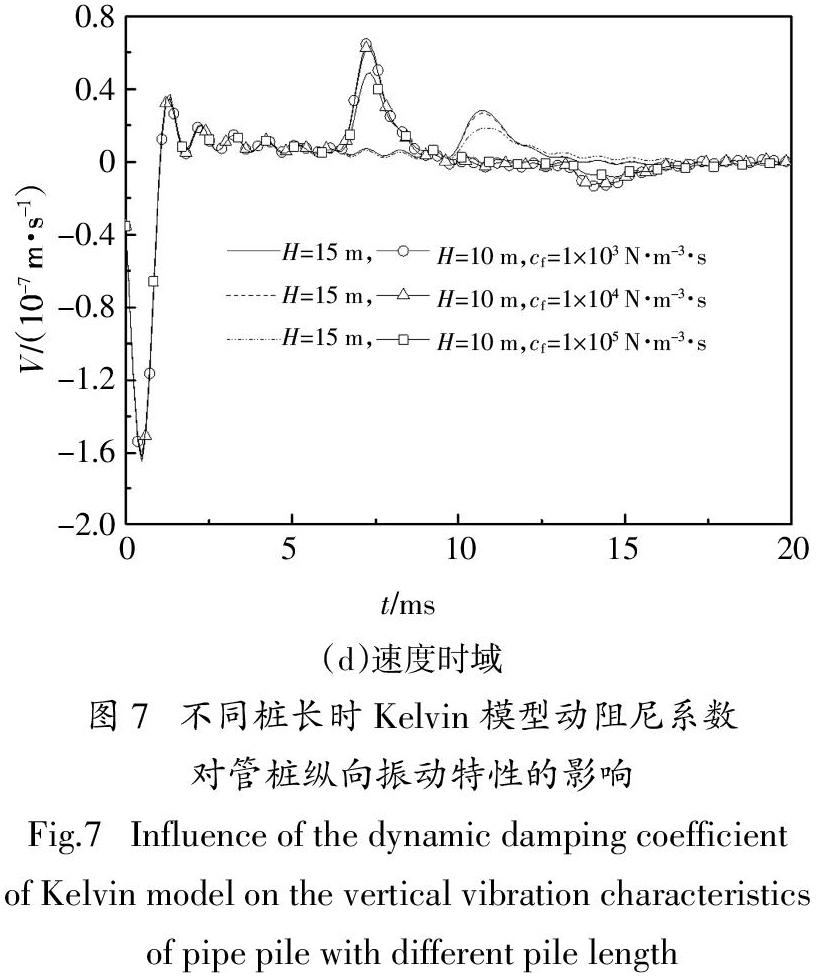
图7反映了不同桩长时Kelvin模型中动阻尼系数对饱和土中管桩纵向振动特性的影响. 桩长H分别设置为10 m和15 m. 由图7可知，随着动阻尼系数的增大，管桩顶部动刚度、动阻尼、速度频域及时域曲线的幅值逐渐减小，且随着桩长的增大，该减小幅度逐渐减小. 以上现象表明，桩长较短时，Kelvin模型中动阻尼系数对管桩纵向振动特性的影响较明显. 后续分析中，为便于研究Kelvin模型中动阻尼系数对饱和土中管桩纵向振动特性的影响，管桩桩长设置为H = 10 m.

5.2   土塞性质影响分析

针对土塞与管桩之间黏结程度不同时，土塞性质对饱和土中管桩纵向振动特性的影响进行了研究，分别分析了饱和土塞的渗透系数、孔隙率、剪切模量及黏性阻尼系数对管桩纵向振动特性的影响.

5.2.1   土塞渗透系数

图8反映了Kelvin模型中动阻尼系数不同时，土塞渗透系数对饱和土中管桩纵向振动特性的影响. 由图8可知，当cf = 1 × 104 N·m-3·s时，随着土塞渗透系数的减小，管桩顶部动刚度、动阻尼、速度频域及时域曲线均基本不变;当cf = 1 × 105 N·m-3·s时，随着土塞渗透系数的减小，管桩顶部动刚度、动阻尼及速度频域曲线的振动幅值略微减小，速度时域曲线的桩端反射信号幅值也略微减小. 这是由于土塞渗透系数较小时，渗透力较大，土塞中固相与液相之间的相互作用耗散的能量较大，土塞对管桩振动能量的耗散能力增强;然本文研究基于端承桩，土塞与外界基本隔离，限制了土塞中固相与液相之间的相互作用，致使土塞渗透系数对饱和土中管桩纵向振动特性的影响较小.

5.2.2   土塞孔隙率

图9反映了Kelvin模型中动阻尼系数不同时，土塞孔隙率对饱和土中管桩纵向振动特性的影响. 由图9可知，当cf = 1 × 104 N·m-3·s时，随着土塞孔隙率的减小，管桩顶部动刚度、动阻尼、速度频域及时域曲线均基本保持不变;当cf = 1 × 105 N·m-3·s时，随着土塞孔隙率的减小，管桩顶部动刚度、动阻尼、速度频域曲线的振动幅值明显增大，速度时域曲线的桩端反射信号幅值也明显增大. 这是由于土塞的孔隙率越小，液相所占比例越小，土塞越密实，土塞中固相与液相之间的相互作用耗散的能量减小，饱和土塞对管桩振动能量的耗散能力减弱.

5.2.3   土塞剪切模量

图10描述了Kelvin模型中动阻尼系数不同时，土塞剪切模量对饱和土中管桩纵向振动特性的影响. 由图10可知，当cf = 1 × 104 N·m-3·s时，随着土塞剪切模量的增大，管桩顶部动刚度、动阻尼、速度频域及时域曲线均基本保持不变;当cf = 1 × 105 N·m-3·s时，仅在低频范围内，随着土塞剪切模量的增大，管桩顶部动刚度、动阻尼及速度频域曲线的振动幅值均略微减小，而速度时域曲线的桩端反射信号幅值基本保持不变. 此现象可做如下解释：此时土塞与管桩之间存在小变形相对滑移，桩土系统振动时，土塞内部变形较小，土塞对管桩振动能量的耗散主要通过土塞的阻尼作用耗散，因此，土塞剪切模量对饱和土中管桩纵向振动特性的影响较小.

5.2.4   土塞黏性阻尼系数

图11反映了Kelvin模型中动阻尼系数不同时，土塞黏性阻尼系数对饱和土中端承管桩纵向振动特性的影响. 由图11可知，当cf =1×104 N·m-3·s时，随着土塞黏性阻尼系数的减小，管桩顶部动刚度、动阻尼、速度频域及速度时域曲线均基本保持不变;当cf =1×105 N·m-3·s时，随着土塞黏性阻尼系數的减小，管桩顶部动刚度、动阻尼及速度频域曲线的振动幅值均明显增大，速度时域曲线的桩端反射信号幅值基本保持不变，这是由于土塞黏性阻尼增大致使土塞对管桩振动能量的耗散能力增强，此现象进一步说明了土塞的阻尼作用对桩身的能量耗散作用较强.

综合上述土塞性质对饱和土中管桩纵向振动特性的影响分析，可知，当Kelvin模型中动阻尼系数cf =1×104 N·m-3·s时，土塞性质对管桩纵向振动特性几乎无影响，此时可认为土塞与管桩黏结程度极弱，土塞与管桩之间产生较大变形的相对滑动. 因此，在本文中，当考虑土塞与管桩小变形相对滑移时，Kelvin模型中动阻尼系数的取值区间可以进一步缩小为：cf = 1×105～1.53×105 N·m-3·s.

6   结   论

本文基于Biot动力固结方程和Kelvin模型，分析了饱和土中非完全黏结管桩的纵向振动特性，得出了以下几点结论：

1）与完全黏结解对比，本文解与工程实际更接近，阐明了Kelvin模型的合理性;本文解的退化解与已有解可很好拟合，验证了本文解的合理性.

2）Kelvin模型中动阻尼系数是影响饱和土中管桩纵向振动特性的主要因素，动刚度系数的影响较小可忽略;动阻尼系数越大，土塞对管桩振动能量的耗散作用越强;Kelvin 模型参数取值可初步确定为：kf = 7.85 × 105 N·m-3，cf = 1 × 105～1.53×105 N·m-3·s.

3）管桩桩长越短，Kelvin模型中动阻尼系数对饱和土中管桩纵向振动特性的影响越明显.

4）土塞与管桩之间为非完全黏结状态时，Kelvin模型中动阻尼系数越大，土塞性质对饱和土中管桩纵向振动特性的影响越明显，其中土塞孔隙率和黏性阻尼系数对饱和土中管桩纵向振动特性有明显影响;土塞剪切模量和渗透系数对土中管桩纵向振动特性影响很小，可以忽略不计.

参考文献

[1]    王海东，尚守平，周志锦，等. 瑞利波作用下桩土相互作用横向动力响应计算研究[J]. 湖南大学学报（自然科学版），2009，36（11）：1—5.

WANG H D，SHANG S P，ZHOU Z J，et al. Computational research on the horizontal dynamic response of single-pile considering pile-soil interaction during passage of rayleigh waves[J]. Journal of Hunan University （Natural Sciences），2009，36（11）：1—5. （In Chinese）

[2]    邹新军，陈少玉，尹帮顺，等. 基桩动力稳定性模型试验研究[J]. 湖南大学学报（自然科学版），2012，39（12）：19—24.

ZOU X J，CHEN S Y，YIN B S，et al. Model test for dynamic stability of piles[J]. Journal of Hunan University （Natural Sciences），2012，39（12）：19—24. （In Chinese）

[3]    刘汉龙，郝小员，费康，等. 振动沉模大直径现浇薄壁管桩技术及其应用（Ⅱ）：工程应用与试验[J]. 岩土力学，2003，24（3）：372—375.

LIU H L，HAO X Y，FEI K，et al. Field pour concrete thin wall cased pile technology and its application（Ⅱ）：application and in-situ test[J]. Rock and Soil Mechanics，2003，24（3）：372—375. （In Chinese）

[4]    刘汉龙，费康，马晓辉，等. 振动沉模大直径现浇薄壁管桩技术及其应用（I）：开发研制与设计[J]. 岩土力学，2003，24（2）：164—168.

LIU H L，FEI K，MA X H，et al. Cast-in-situ concrete thin-wall pipe pile with vibrated and steel tube mould technology and its application （I）：development and design[J]. Rock and Soil Mechanics，2003，24（2）：164—168. （In Chinese）

[5]    劉汉龙，丁选明. 现浇薄壁管桩在低应变瞬态集中荷载作用下的动力响应解析解[J]. 岩土工程学报，2007，29（11）：1611—1617.

LIU H L，DING X M. Analytical solution of dynamic response of cast-in-situ concrete thin-wall pipe piles under transient concentrated load with low strain[J]. Chinese Journal of Geotechnical Engineering，2007，29（11）：1611—1617. （In Chinese）

[6]    刘汉龙，张建伟，彭劼. PCC桩水平承载特性足尺模型试验研究[J]. 岩土工程学报，2009，31（2）：161—165.

LIU H L，ZHANG J W，PENG J. Full-scale model tests on behavior of cast-in-place concrete pipe piles with large diameter under lateral loads[J]. Chinese Journal of Geotechnical Engineering，2009，31（2）：161—165. （In Chinese）

[7]    費康，刘汉龙，周云东，等. 现浇混凝土薄壁管桩单桩性状简化分析[J]. 河海大学学报（自然科学版），2004，32（1）：59—62.

FEI K，LIU H L，ZHOU Y D，et al. Simplified analysis of performance of in-situ concrete thin-wall pipe piles[J]. Journal of Hohai University（Natural Sciences），2004，32（1）：59—62. （In Chinese）

[8]    费康，刘汉龙，张霆. PCC桩低应变检测中的三维效应[J]. 岩土力学，2007，28（6）：1095—1102.

FEI K，LIU H L，ZHANG T. Three-dimensional effects in low strain integrity test of PCC pile[J]. Rock and Soil Mechanics，2007，28（6）：1095—1102. （In Chinese）

[9]    DING X M，ZHENG C J，LIU H L. A theoretical analysis of vertical dynamic response of large-diameter pipe piles in layered soil[J]. Journal of Central South University，2014，21（8）：3327—3337.

[10]  丁选明，刘汉龙. 大直径管桩在瞬态集中荷载作用下的振动响应时域解析解[J]. 岩土工程学报，2013，35（6）：1010—1017.

DING X M，LIU H L. Time-domain analytical solution of the vibration response of a large-diameter pipe pile subjected to transient concentrated load[J]. Chinese Journal of Geotechnical Engineering，2013，35（6）：1010—1017. （In Chinese）

[11]  ZHENG C J，LIU H L，DING X M，et al. Resistance of inner soil to the vertical vibration of pipe piles[J]. Soil Dynamics and Earthquake Engineering，2017，94：83—87.

[12]  郑长杰，丁选明，栾鲁宝. 黏弹性地基中管桩水平动力特性分析[J]. 岩土力学，2017，38（1）：26—32.

ZHENG C J，DING X M，LUAN L B. Analysis of lateral dynamic response of pipe pile in viscoelastic soil layer[J]. Rock and Soil Mechanics，2017，38（1）：26—32. （In Chinese）

[13]  吴文兵，蒋国盛，王奎华，等. 土塞效应对管桩纵向动力特性的影响研究[J]. 岩土工程学报，2014，36（6）：1129—1141.

WU W B，JIANG G S，WANG K H，et al. Influence of soil plug effect on vertical dynamic response of pipe piles[J]. Chinese Journal of Geotechnical Engineering，2014，36（6）：1129—1141. （In Chinese）

[14]  WU W B，EL NAGGAR M H，ABDLRAHEM M，et al. A new interaction model for the vertical dynamic response of pipe piles considering soil plug effect[J]. Canadian Geotechnical Journal，2017，54（7）：987—1001.

[15]  LIU H，JIANG G S，EL-NAGGAR M H，et al. Influence of soil plug effect on the torsional dynamic response of a pipe pile[J]. Journal of Sound and Vibration，2017，410：231—248.

[16]  LIU H，WU W B，JIANG G S，et al. Influence of soil plug effect on the vertical dynamic response of large diameter pipe piles[J]. Ocean Engineering，2018，157：13—25.

[17]  LIU H，WU W B，JIANG G S，et al. Benefits from using two receivers for the interpretation of low-strain integrity tests on pipe piles[J]. Canadian Geotechnical Journal，2019，56（10）：1433—1447.

[18]  刘林超，闫启方. 饱和土中管桩的纵向振动特性[J]. 水利学报，2011，42（3）：366—372.

LIU L C，YAN Q F. Vertical vibration characteristics of pipe pile in saturated soil[J]. Journal of Hydraulic Engineering，2011，42（3）：366—372. （In Chinese）

[19]  郑长杰，刘汉龙，丁选明，等. 饱和黏性土地基中现浇大直径管桩水平振动响应解析解[J]. 岩土工程学报，2014，36（8）：1447—1454.

ZHENG C J，LIU H L，DING X M，et al. Analytical solution of horizontal vibration of cast-in-place large-diameter pipe piles in saturated soils[J]. Chinese Journal of Geotechnical Engineering，2014，36（8）：1447—1454. （In Chinese）

[20]  靳建明，张智卿，吴章土，等. 饱和土中管桩的扭转振动特性研究[J]. 振动与冲击，2015，34（11）：52—57.

JIN J M，ZHANG Z Q，WU Z T，et al. Torsional vibration of a pipe pile embedded in a porous-saturated soil[J]. Journal of Vibration and Shock，2015，34（11）：52—57. （In Chinese）

[21]  ZHENG C J，HUA J M，DING X M. Torsional vibration of a pipe pile in transversely isotropic saturated soil[J]. Earthquake Engineering and Engineering Vibration，2016，15（3）：509—517.

[22]  李强，王奎华，谢康和. 饱和土中端承桩纵向振动特性研究[J]. 力学学报，2004，36（4）：435—442.

LI Q，WANG K H，XIE K H. Vertical vibration of an end bearing pile embedded in saturated soil[J]. Chinese Journal of Theoretical and Applied Mechanics，2004，36（4）：435—442. （In Chinese）

[23]  LIU H L，ZHENG C J，DING X M，et al. Vertical dynamic response of a pipe pile in saturated soil layer[J]. Computers and Geotechnics，2014，61：57—66.

[24]  杨峻，吴世明，蔡袁强. 饱和土中弹性波的传播特性[J]. 振动工程学报，1996，9（2）：128—137.

YANG J，WU S M，CAI Y Q. Characteristics of propagation of elastic waves in saturated soils[J]. Journal of Vibration Engineering，1996，9（2）：128—137. （In Chinese）

[25]  RANDOLPH M F，MAY M，LEONG E C，et al. Soil plug response in open-ended pipe piles[J]. Journal of Geotechnical Engineering，1992，118（5）：743—759.

[26]  王建華，智胜英. 低应变条件下桩土相互作用的阻尼系数[J]. 岩石力学与工程学报，2007，26（9）：1800—1808.

WANG J H，ZHI S Y. Damping coefficients of pile-soil interaction with low strain[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26（9）：1800—1808. （In Chinese）