基于点对局部拓扑和加权二分图的地面目标关联
2021-02-21吉琳娜杨风暴
夏 涛,吉琳娜,刘 哲,杨风暴
(中北大学信息与通信工程学院,山西 太原 030051)
0 引言
随着各种探测技术的迅速发展,侦察设备所获取的关于地面目标的信息量急剧增加,信息来源也更加丰富。如何挖掘信息背后隐藏的关系,把相应的观测信息与同一目标进行匹配,是当前侦察领域非常关心的一个问题。地面目标关联可以利用异类传感器的观测序列中获取的地面目标的量测信息,将不同传感器获取的同一目标的信息进行匹配,实际上解决的是一个异类传感器目标配对的问题[1]。
国内外学者对关联算法进行了大量的研究,已发展为应用于多领域的重要技术。文献[2]在使用目标位置信息进行关联匹配时,要引入目标的属性特征对基于位置信息的粗关联结果进行修正,但这类算法一般复杂度高,且通常难以建立相对完备的目标特征数据库。而基于位置信息的目标关联方法是目前比较成熟的关联方法,其大致分为两类:一是基于目标运动状态信息的方法;二是基于点模式匹配的方法。经典的目标关联方法有最近邻算法(NN)[3]、概率数据关联算法(PDA)[4]、联合概率数据关联算法(JPDA)[5]、多假设跟踪方法(MHT)[6]等。这些算法一般都是利用目标的运动状态信息,通过传感器不同时刻获取的目标状态信息进行关联;但由于地面背景复杂、易受杂波干扰,地面目标具有强机动性,要求观测信息时间分辨率高等因素,往往难以建立有效的运动模型估计和预测目标的真实轨迹,极大地影响了关联正确率。迭代最近点(ICP)[7]算法是应用最广泛的点模式匹配算法之一,因为它实现简单,计算复杂度低;然而,ICP算法需要满足一定的要求,即两个点集的初始位置应当保持较小的距离,在实际中并非总是如此。文献[8]使用了形状上下文(SC),该算法比ICP算法具有更强的鲁棒性,但其也有明显的局限性,即一个形状中的邻近点对可能与另一个形状中相距较远的两个点匹配。
综上所述,大多基于位置信息的目标关联算法都存在局限性,制约了关联正确率的提高。基于全局拓扑特征的关联方法鲁棒性好,但当点集中点的位置包含较多噪声时关联正确率下降。为此,本文提出基于PPLT-WBGM的地面目标关联方法。
1 形状描述算子与加权二分图
1.1 形状描述算子
1.1.1 点对全局拓扑


(1)

(2)

图1(a)和图1(b)分别为全局拓扑特征的构造方法和全局拓扑特征描述算子。该方法具体如下:计算点集S中任意两点之间的欧氏距离,在所有的欧式距离中选出中值作为半径,得到点si的邻域,并计算该邻域的质心msi。以si为原点,画出五个同心圆,向量simsi作为极径,按照离原点的对数距离logρ依次量化为{1,2,3,4,5}五个整数值,角度按照逆时针方向依次均匀量化为{0,1,2,3,…,11}十二个整数值,整个邻域空间按对数极坐标划分为60个部分。

图1 全局拓扑特征描述算子Fig.1 Global topological characteristic descriptor
全局拓扑特征方法对于平移、旋转等刚性变换甚至微小的非刚性变换具有较强的鲁棒性[10];但是,当点集中点的位置包含较多噪声时,此方法的鲁棒性恶化比较明显。第一,由于点si的邻域在全局拓扑特征上在直角坐标系下是非均匀量化的,距离原点si越近的邻近点对噪声越敏感,尤其是角度量化时,靠近原点si的邻近点更容易偏离到其他区域甚至是相反的区域;第二,因为邻域的质心被选定为参考点,当点集中出现较多异常值时,参考点的位置与真实位置相比误差较大。
1.1.2 点对局部拓扑


图2 点对局部拓扑特征描述算子Fig.2 Point pair local topological characteristic descriptor
1.2 加权二分图
二分图又称为二部图,是图论中的一种特殊模型。设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),其中,两点之间的连线表示G的边,并且图中的每条边(i,j)所关联的两个顶点分别属于这两个不同的顶点集A和B,则称图G为一个二分图。设ai,bj(i,j=1,2,…,n)分别是顶点集A、B中的点,给连接两顶点的边上赋予相应的权值wij,其数值大小在0到1之间,且每个点只能选择一次。由图G中一些不相邻的边组成的集合M称为G的一个匹配。图G的含边数最多的匹配称为G的最大匹配。设l是赋权二部图G的一个可行顶点标号,若相等子图Gl有完美匹配M′,则M′是G的最大权完美匹配。
2 基于PPLT-WBGM的地面目标关联方法
为了提升算法的抗噪性能和鲁棒性,本文提出基于PPLT-WBGM的地面目标关联方法,首先构建点对局部拓扑特征,使用特定的点代替全局拓扑特征中的质心,并采用欧式距离代替对数距离进行均匀量化,降低了对噪声的敏感性和算法复杂度;其次计算不同点集中点对之间的相似度,得到相似度矩阵;最后建立加权二分图,将该点模式匹配问题转化为在加权二分图中寻找最大权完备匹配的问题,并使用Kuhn-Munkres算法进行最佳匹配求解,实现地面目标关联。具体流程如图3所示。

图3 基于PPLT-WBGM的地面目标关联方法流程图Fig.3 Flow chart of ground target association method based on PPLT-WBGM
2.1 点对局部拓扑特征构建

Smim,jn=(1-λ)SoDim,jn+λSoAim,jn
(3)
(4)
(5)
(6)
对得到的拓扑特征的相似度矩阵,为了使邻域A和B中的点相互匹配,需要给出一定的规则寻找最佳匹配[12],也即实现目标关联正确率最高。
2.2 实现最佳匹配
目标关联的本质就是在目标检测的基础上寻找最优的关联目标对[13]。若不同的观测信息都来源于同一个目标,那么这些观测信息之间的相似度必然较大。因此,结合二分图定义,基于点模式匹配的目标关联过程就可以映射为加权二分图匹配过程[14],并通过某些算法实现最佳匹配。而完成最佳匹配,只需在相似度矩阵SM中寻找一组不在同一行或同一列的元素,使得该组元素和最大,即全局相似度最大。相似度矩阵SM可以用二分图G来表示,传感器a和b检测到的目标集A和B作为二分图不同的顶点集,相似度矩阵中的元素Smim,jn可以用顶点之间被赋予权重的边来表示,如图4所示。寻找每个am与某个bn的匹配,使得权重和最大,则完成了最佳匹配,如图4中实线所示。

图4 相似度矩阵的加权二分图Fig.4 Weighted bipartite graph of similarity matrix
常见的匹配算法有贪心算法、匈牙利算法等。贪心算法思想简单明了,但求解时不从整体最优上加以考虑,所得到的仅是在某种意义上的局部最优选择,因此不适合二分图最佳匹配。而Kuhn-Munkres算法不仅十分适合求解加权二分图匹配问题,与枚举法相比,其计算复杂度也大大下降。Kuhn-Munkres算法基本思想为首先给出加权二部图G的任意一个可行顶点标号,然后决定相等子图G,在Gl中执行匈牙利算法。根据最大权完美匹配定义可知,若在Gl中找到完美匹配,它就是G的最大权完美匹配。
3 实验与分析
假定地面某车辆群中有9个车辆目标,其真实位置坐标分别为[0,100]km内随机生成的数据,目标分布如图5中正方形所示。由于传感器的定位误差受到噪声干扰等因素,传感器a和传感器b得到的位置信息均有一定的误差,把两者的总误差分别记为Eg和Ee,并设定Eg和Ee分别服从零均值高斯分布N(0,σg)和N(0,σe)。在目标点集的真实位置上添加均值为零和方差分别为Eg和Ee的噪声,得到传感器a和b的目标点集,如图5中“*”和“o”所示。
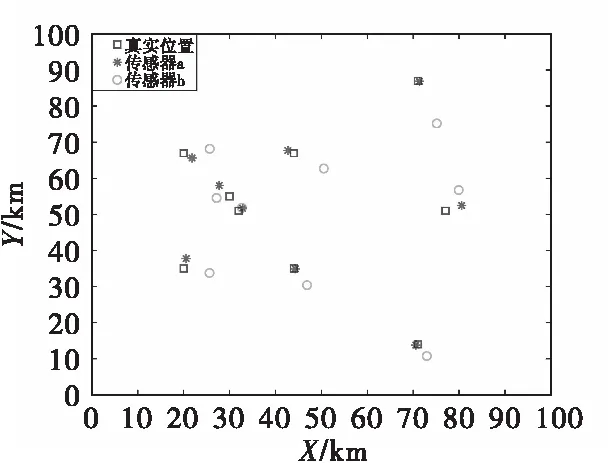
图5 目标位置示意图Fig.5 Diagram of target positions
传感器a总误差中σg有两种可能取值:{0.2,1} km,而传感器b总误差中σe有三种可能取值:{4,7,10} km。为了验证本文方法的有效性,针对无目标漏检和有目标漏检两种情况下的场景分别进行四组仿真实验,并与最近邻方法(NN)和重心坐标匹配算法(BCM)进行了对比,每组实验进行蒙特卡罗仿真1 000次,实验结果如表1—表4所示。

表1 Eg=0.2 km且无目标漏检时的正确匹配率比较Tab.1 Comparison of matching accuracy with Eg=0.2 km and no missed target
表1和表2分别展示了传感器a误差中σg分别取0.2 km和1 km,且不存在目标漏检时不同算法的正确匹配率比较。可以明显地观察到,本文方法和BCM算法的正确匹配率远高于NN方法。图6为三种算法的关联正确率比较曲线,实线、虚线分别表示Eg取值为0.2 km和1 km。随着传感器的误差不断增大,三种方法的正确匹配率都有不同程度的下降,但本文方法性能下降幅度相对较小,如图6(a)所示,其性能仍然优于NN方法和BCM算法。NN方法只是将落在关联门内且与目标的预测位置最邻近的观测点作为相关联的观测,其抗干扰能力弱,所以传感器误差增加时易发生关联错误。而对于BCM算法来说,传感器的误差增加,目标群的重心位置与实际位置偏差较大,导致其正确匹配率大幅下降。

表2 Eg=1 km且无目标漏检时的正确匹配率比较Tab.2 Comparison of matching accuracy with Eg=1 km and no missed target
为了模拟真实环境中的目标漏检情况,在传感器b的目标集中随机删除一个目标,实验结果如表3、表4所示。结合表1—表4和图6可以发现,与不存在目标漏检时相比,目标漏检情况下NN方法的正确匹配率下降约5%~8%,BCM算法的正确匹配率下降约15%,而本文方法仍可以保持较高的正确匹配率。综合以上实验可以得出结论:面对传感器误差增大、存在目标漏检时,本文方法的正确匹配率较高。
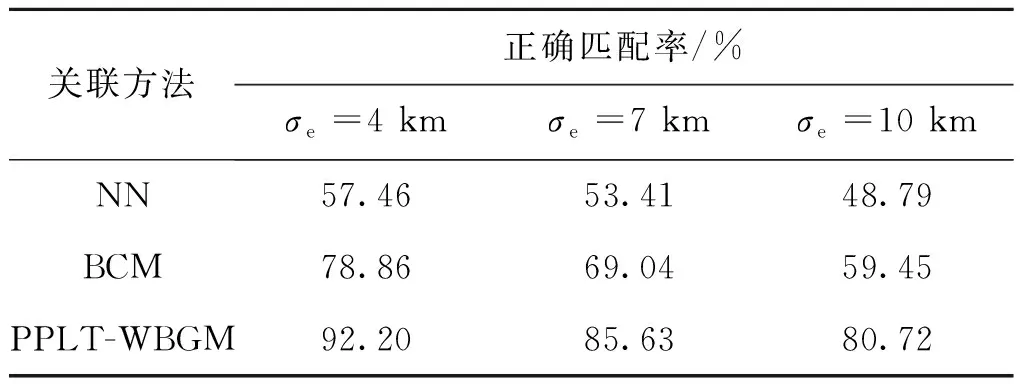
表3 Eg=0.2 km且漏检一个目标时的正确匹配率比较Tab.3 Comparison of matching accuracy with Eg=0.2 km and missed one target

表4 Eg=1 km且漏检一个目标时的正确匹配率比较Tab.4 Comparison of matching accuracy with Eg=1 km and missed one target

图6 关联正确率比较Fig.6 Correlation accuracy comparison
4 结论
本文提出一种基于点对局部拓扑和加权二分图匹配的地面目标关联方法。该方法采用点对局部拓扑特征刻画目标群中各个成员目标之间的相对位置关系,提高了形状描述算子的抗噪能力。根据全局相似度最大的要求,基于点模式匹配的目标关联问题可以转化为加权二分图匹配问题。最后构建了加权二分图,并通过改进的Kuhn-Munkres算法实现最佳匹配。仿真实验表明,在位置信息存在偏差和目标漏检的情况下,该算法与传统方法相比具有较高的关联正确率和较强的鲁棒性。
