基于多传感器信息融合技术的SCI-AUFK滤波器

万珊珊，孙 青，翁明善，于学呈，郑桂妹

(1.空军工程大学防空反导学院，陕西 西安 710051;2.解放军93159部队， 辽宁 大连 116033)

0 引言

多传感器网络系统可广泛应用于目标跟踪、环境监测以及雷达探测、卫星导航等系统，受到了越来越多学者的关注。在多传感器网络系统中，由于微积分计算的复杂，一般不能直接求得精确的最优解，因此，相关研究学者提出了多种近似的滤波方法。文献[1—2]提出了扩展Kalman滤波(EKF)算法，对于多传感器非线性系统的滤波，EKF算法有明显的效果；但缺点是其采用近似化的方法进行处理，在过程中省略了泰勒展开式的高阶部分的运算，引入了多余的系统误差，同时其雅可比矩阵的计算复杂，计算负担较大。文献[3]提出了无迹Kalman滤波(UKF)算法，避免了雅克比问题，可用于实时估计系统；但是UT变换基础是以高斯概率分布为条件的，该算法不适用于非高斯系统。文献[4]应用UKF算法的新息序列设计了一种自适应无迹Kalman滤波(AUKF)算法，以估算测量噪声的统计特性，实现了量测噪声统计特性的在线估计。

对于多传感器CI融合估计，文献[5]通过对多个局部传感器的无偏估计值联立进行融合处理，提出了批处理协方差交叉(BCI)融合器，但增加了计算负担。为了减少复杂度和计算量，通过顺序处理，文献[6]提出了一种基于序列处理方法的快速融合估值器，即SCI融合器。本文针对以上问题，利用AUKF估算测量噪声的统计特性[7-8]，对于带不确定噪声方差的雷达网系统，在自适应无迹Kalman滤波(AUKF)方法的基础上，提出SCI融合自适应无迹Kalman滤波器(SCI-AUKF)，可有效解决未知噪声的多传感网络系统的状态估计问题。

1 多传感器网络系统状态估计问题

设多传感网络系统模型的状态方程与观测方程为：

x(k+1)=f(x(k),k)+w(k)

(1)

y(i)(k)=h(i)(k)(x(k),k)+v(i)(k),i=1,…，L

(2)

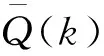
(3)

针对多传感网络系统，已知其噪声保守上界，对于不确定噪声方差的状态估计问题提出SCI-AUKF融合算法。

2 SCI融合自适应无迹Kalman滤波器

2.1 自适应无迹Kalman滤波器

在UT变换的基础上，结合最小偏度单形采样策略[9]和自适应调整量测噪声式[10]相关理论，对UKF进行优化与改进。AUKF算法流程如下:

步骤1 初始化。

(4)

步骤2 进行改进后的UT变换，求Sigma点。

步骤3 进行时间更新。由步骤2利用非线性状态方程最终计算出状态估计值以及误差协方差阵。

γ(k|k-1)=f(χ(k),u(k-1))

(5)

(6)

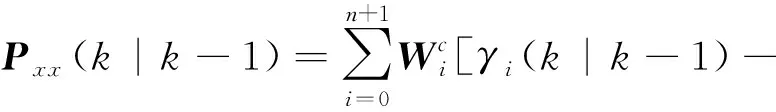
(7)

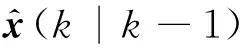
步骤4 对量测值进行更新。

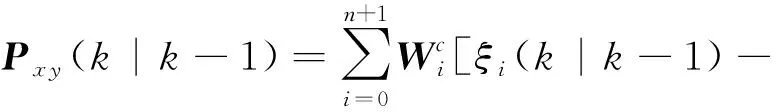
(8)

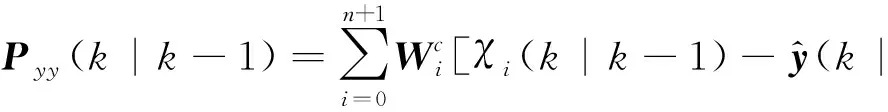
(9)

(10)

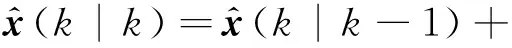
(11)

Pxx(k|k)=Pxx(k|k-1)-
K(k)Pyy(k|k-1)K(k)T

(12)

式(8)—式(12)中，Pxy表示x与y的协方差阵，Pyy表示y与y的协方差阵，K表示卡尔曼滤波增益。

2.2 改进的自适应无迹Kalman滤波器

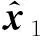
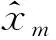
(13)

(14)

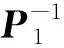
(15)

则Ω就是PCI的协方差椭圆，即：

(16)

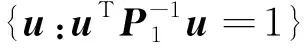
(17)

则有：

(18)

(19)

(20)

(21)

(22)

将式(20)带入式(21)和式(22)即可得到CI融合算法。

(23)

(24)

基于自适应无迹Kalman滤波器式(11)和式(12)应用CI融合算法式(21)和式(22)，即可以得证式(23)与式(24)。

本文提出的SCI-AUKF滤波算法主要是针对多传感器网络系统，在本文应用于雷达网跟踪系统。现将局部雷达1与局部雷达2通过CI-AUKF得到结果再与雷达3进行融合，依次类推，直到第L个雷达参与融合，故其融合精度应高于任意一个局部滤波器的估计精度。在文献[11]中提及到SCI融合器的估计精度关于融合的次序不是很灵敏，但是却便于实际操作。

SCI-AUKF估计原理由(L-1)步实现，如下：

⋮

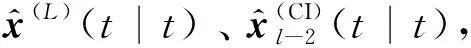
(25)

(26)

重复利用两传感器CI-AUKF式(23)和式(24)，则SCI-AUKF可用L-1个两传感器CI-AKUF递推实现，即可证明对于不确定噪声方差的非线性系统(1)和(2)在满足式(3)的情况下，即可得到的序贯协方差交叉融合自适应无迹Kalman滤波器为：

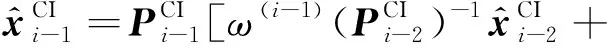
(27)

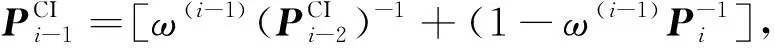
(28)

引理1 局部状态估计与融合状态估计的精度关系[12]：

P(CI)≤P(i),i=1,…,L

(29)

trP(m)≤trP(SCI)≤trP(i),i=1,…,L

(30)

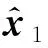
成立。则SCI-AUKF 算法的精度高于局部稳态滤波器算法估计值的精度，P(m)表示用矩阵加权的状态融合估计误差方差。

3 仿真分析

为了验证 SCI-AUKF融合算法的有效性和优越性，在3部雷达组网系统中进行仿真研究。其状态方程为：

x(t+1)=Φx(t)+Γw(t)

(31)

yi(t)=Hix(t)+vi(t),i=1,2,3

(32)

式(31)中，

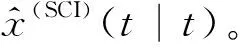
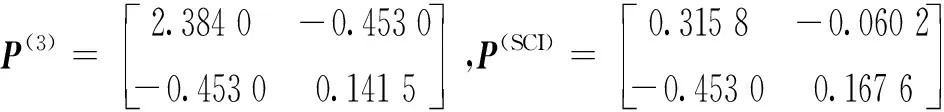
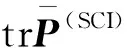
表1 各Kalman滤波器的精度Tab.1 The accuracy of each kalman filter

表2 SCI-AUKF滤波器与BCI-AUKF滤波器的精度比较Tab.2 Comparison of accuracy between SCI-AUKF and BCI-AUKF

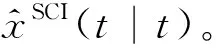
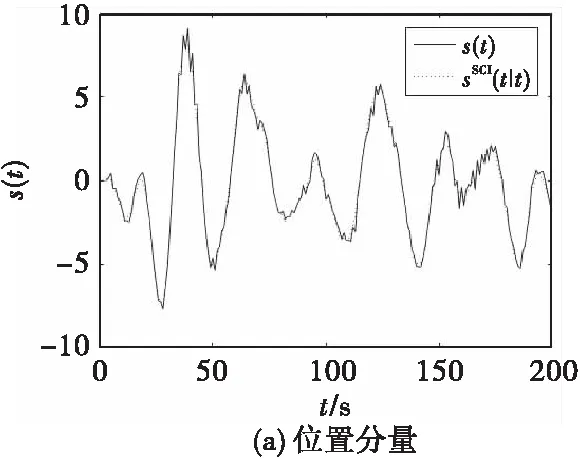
图1 位置和速度分量的跟踪估计Fig.1 Tracking estimation of position and velocity components

根据滤波误差平方和[12]

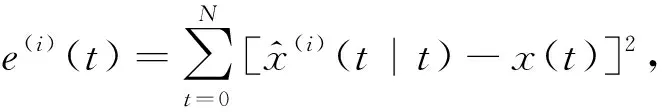
(32)

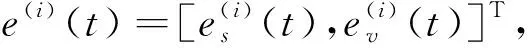
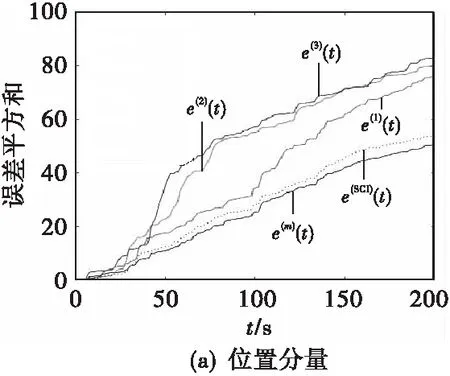
图2 滤波误差平方和Fig.2 Filter error covariance

通过仿真，协方差椭圆曲线如图3所示，其中，P(i),i=1,2,3分别为第i个局部稳态传感器的估计误差方差，P(m)为按矩阵加权融合滤波器的估计无差方差。可看出协方差椭圆P(SCI)和协方差椭圆P(m)是最里面的部分，这表明矩形加权融合滤波器的估计精度是最高的，SCI-AUKF融合滤波器比局部滤波器具有更好的保守性能，即估计精度更高。

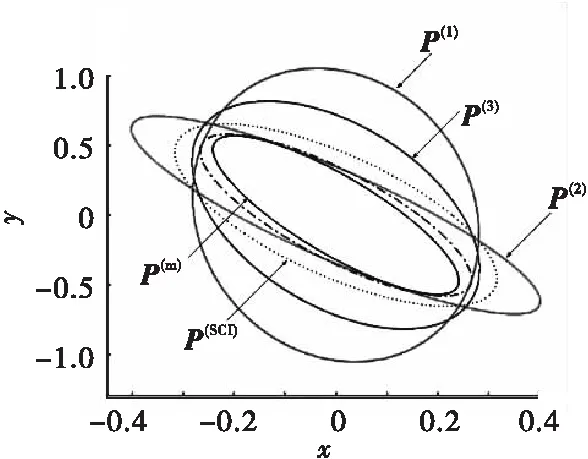
图3 误差方差P(i),i=1,2,3,m,SCI和的协方差椭圆曲线Fig.3 The covariance ellipse curves of error variances

4 结论

本文提出基于多传感器网络系统的SCI-AUKF滤波器，该方法在序列处理的基础上，提出序贯协方差交叉融合自适应无迹Kalman滤波器，当传感器数量较大时，通过递归处理可以明显降低计算量和复杂度。仿真验证结果表明SCI-AUKF融合滤波器优于各局部滤波器，相比BCI融合滤波器的精度有明显提升。同时也说明SCI-AUKF滤波器针对多传感网络系统，对不确定噪声方差下的状态估计问题具有良好的性能。