基于C-W节约算法的快递配送路径优化研究
2021-02-19时宇



摘 要:随着经济社会网络管理信息化的发展,快递的数量逐年递增,人们对快递配送的时间要求越来越高,提高快递配送服务的效率也愈发显得重要,因此做好快递配送路径的优化以提高配送效率具有十分重要的意义。本文针对快递配送路径优化这一问题进行探讨,为解决该问题而建立TSP模型,并以C-W节约算法对其进行求解来解决由于没做好路径优化而导致快递延误送达的问题,提高消费者的满意度。
关键词:路径优化;TSP模型;C-W节约算法
中图分类号:TP312 文献标识码:A文章编号:2096-4706(2021)13-0121-04
Research on Express Delivery Path Optimization Based on C-W Saving Algorithm
SHI Yu
(Liaoning University of International Business and Economics, Dalian, 116052, China)
Abstract: With the development of economic social network management informatization, the number of express is increasing year by year. People have higher and higher requirements for the time of express distribution, and it is more and more important to improve the efficiency of express distribution service. Therefore, it is of great significance to optimize the express distribution path to improve the distribution efficiency.This paper discusses the problem of express delivery path optimization, and establishes TSP model to solove the problem, and solves it with C-W saving algorithm to solve the problem of express delay delivery caused by failure to do well in path optimization, so as to improve consumers’ satisfaction.
Keywords: path optimization; TSP model; C-W saving algorithm
0 引 言
随着我国社会经济和互联网电子商务的蓬勃发展,快递行业已经逐渐走进了千家万户。根据统计数据资料显示2019年我国的快递服务量已经突破600亿件,累计完工635.2亿件,我国的快递公司日均办理货物能力已经超过1.7亿件,日最大处理能力5.4亿件。2020年以来我国的国内快递业务数量更是已经再次走向了一个具有历史性的增长新台阶,国家邮政局再次明确指出自2020年9月10日起,从去年我国的国内快递配送业务量已经首次达到500亿件的大规模以来,每月都有望能够再次快速登上百亿级的历史台阶,实现"四连跳"增长直至再次超过去年突破800亿件的规模大关,创造了当年以来我国国内快递业务行业数量发展快速历史的最高数量记录。近年来,快递行业蓬勃发展,快递数量也在急速增长,想要在快递量持续增加的前提下,使得快递送到客户手中的时间缩短,快递的配送这一环节就显得尤为重要。而快递是与消费者直接接触的物流活动,其成本占据了整个企业(物流公司)成本的很大一部分。快递运输路线的合理性对于整个快递配送过程中的速度、成本、效益都有着很大的重要影响,特别是针对某一地区或者某一客户的快递运输路线更加复杂。因此,运用科学合理的方法优化配送路线是快递配送中非常重要的一个环节。那么为了我们可以及时快速地把所有货物运送到广大客户的手中,提高了公司对于客户的服务和满意程度,同时还能够提高我们公司的社会经济效益,在配送的过程中,快递配送路径优化就成了整个配送网络优化的关键环节。它不但可以有效地减少商品的配送工作时间与里程,提高了配送的效率,还能够大幅度地提高汽车的利用率,降低了配送的成本。因此,如何优化配送路径进而节约配送里程已经成了一个急需解决的问题。
目前,随着快递量的增加,尤其双十一、618等活动后,许多人都开始关注快递配送的路径优化问题。例如蔺士文,杨金云,吴昊龙,张月,龚志成等人建立了一套VRP模型,利用节约里程法,优化和设计物流配送的路径。都雪静,孙菲菲,王云浩建立了一个成本最低、交付货物时间最短、碳排放最少的多目标汽车行驶路径相关性问题的模型,并用遗传算法进行求解。叶润舟利用改进的混合粒子群算法解决"最后一公里"的配送优化展问题。谢伟以京东达达物流公司为例对其进行了分析,用 matlab 软件对其进行了编程,结合 VRP 模型,解决了同城配送的快递问题。本文从配送的路径问题入手,对其构建TSP模型,并利用C-W 节约算法进行求解。
1 快递配送路径优化的主要概念
1.1 快递配送的概述和主要步骤
配送是指按照客户对商品订单的需求分类,在配送中心进行配送,并及时将相应的货物送到客户手中的活动。它是一种生产或者消费之间相互联系的中介,涉及物流活动主要是指根据客户订单需求配送货物,在自己的物流服务中心向客户分发货物并及时把这些货物运输给收货人。配送环节是整个物流环节中重要组成环节,主要分为以下步骤:(1)公司收货:即应客户要求或公司卖方联系业务接收货物。一般来说,大型物流公司是拥有自己长期合作关系和大量货物的客户,其中一些通常會找到客户的货物并将其运送到他们的家中。(2)车辆的装载:主要由公司运营管理部门负责执行,将根据顾客的时效需求对其做出相应的安排。装载原则上就是尽量有效利用和充分合理的车辆空间。(3)运输:将货物运送到枢纽,与驾驶员保持良好的沟通。(4)到达枢纽处:到达时卸下货物。卸货时,可以根据货物的目的地不同放在不同的地方。(5)分类:可以根据目的地不同对货物进行分类,如将旅顺口区放在一起、将甘井子区放在一起以便于运输,货物少时也可以直接装上。(6)过车:装载运输货物的机动车辆抵达后直接把运输货物交付到送货车上,并在装车前将货物归档。即在进行装车时对所有需要的装车货物的相关信息都进行了电子记录,其中所有货物的相关信息主要包括有装车的时间、配送员、配送人员的电话、发货地、目的地、客户姓名、客户电话等基本信息。记录完成后,需要在电脑中将信息汇编到计算机中,打印纸质面单,以便于进行货物的分配。(7)派送货物:派送员将所需派送的货物送到客户手中,且对派送的货物进行处理。在派送过程中可能出现货物仍需中转,货物分拣错误等情况,派送员需要对这些具体问题进行具体分析。如果在派送中有由于特殊原因不能按时交货的情况出现,派送员要及时地进行沟通。(8)客户签收:为客户配送之前客服或进行配送的人员要及时与客户取得联系,以沟通交货时间和货物到达时的交货地点等基本情况。为了避免与客户不必要的纠纷,需要看清客户在签收单上的备注并加以注意,在货物送达后,需客户验收货物确定货物没有问题并在签收单上签字后视为配送成功。
1.2 配送路径优化的意义
配送路径优化是配送优化中的一个重要环节。在配送的过程中,配送的路径是否合理对配送的速度,成本和收益有重大影响。设计合理,有效的配送途径,不仅可以大大缩短物流配送的时间,降低运营成本和改善运营效果,而且还可以带来更好的客户服务,更高的客户满意度和良好的公司形象。配送路径的合理性对交付速度,成本和收益产生重大影响,尤其是对于快递这样的多个用户而言,配送的路径更为复杂,对配送过程的路径做出优化就更有意义。配送的合理化是否正确是整个物流过程中配送路径是否能够得到合理化的一个重要组成部分,而且这也是配送过程能够得到正确性的关键。所以配送途径优化在整个企业、社会中都非常有重大的作用。
1.2.1 缩短企业配送时间
对于公司来说,优化配送途径和路线就能够缩短配送的时间及公里数,进而改善配送的效率。配送管理效率的改善不仅能够增加车辆在行驶过程中的使用量,降低了企业在运输过程中所需要的时间費用,还能及时地将商品送达顾客,提高了顾客的满意度;不仅能够如此,对配送途径问题进行分析和优化还能够使整个公司在物流配送中的工作过程变得更加合理化,提升自己公司的作业效率,这样一来更加有利于增强我国公司在物流行业中的市场竞争能力和效果。
1.2.2 降低社会非必要成本
对于整个现代化社会来说,优化货物配送的路线不仅能够节省运输人员和车辆,降低了空车的概率,降低了社会的物流费用和成本,同时,它还能够缓解交通紧张,减少运输过程中的污染。例如噪音和废气。
2 TSP模型的建立
2.1 TSP模型概念
TSP问题模型,也可称为旅行者问题,首先被认为是1759年欧拉所研究的一个骑士巡回问题,1948年美国RAND公司于此推出。 TSP问题被认为是最基本的道路问题,该问题是在寻求由一个旅行商从固定原点出发,遍历过所有需要到达的定点后再回到固定原点的最小路径成本。
2.2 建立TSP模型的核心思想
TSP问题的在物流学中所说的描述就是指对应于一个物流配送企业,欲将n个客户的所有订货沿着最短时间路线完整地运送到。就是指从以我们为主要服务的物流配送中心为出发点,将所有的货物运送到n个客户手中的(n-1)!条路线中选取距离最短的那一条。即已知起始点和其他点之间的距离,寻找一条路径使起始点和其他点之间的路径总和最小。并且两两点之间都有直达的路线,这条路线不需要经过中间其他点或偶尔有两个点之间的路线需要经过其他中间点。
2.3 模型建立的步骤
首先,找到起始的点A,得到起始点A与其他点之间B、C、D、E、F、G的距离,并将点与点之间的距离整理成点距离表格。接着,用圆圈来表示需要到达的每一个点,并对每一个点进行标号,用线段来表示点与点之间的距离并且根据画出模型图。最终要求找到一条路线遍历所有的点使得点与点的距离和最小。
3 C-W节约算法的概述和主要步骤
3.1 C-W节约算法的概述
C-W节约算法是克拉克和赖特于1964年提出的求解汽车路径问题的一种启发式构造方法。其基本理念就是首先把各个已经拥有的定点和所在原点0(也就是配送中心)连接起来,构成一条包含所有定点且最终能够返回到所在原点0的运输路线。总费用是指以两倍于原点连接到各个固定定点之间距离的费用,然后通过计算使点i和j分别连接在同一条线路上的费用“节约值”:S(i,j)=c0i+ci0+c0j+cj0-(c0i+cij+cj0)= ci+c0j-cij
S(i,j)越大,说明把i和j,连接在一起时总路程减少越多。
该公式中S(i,j)表示节约的路径距离,c0i表示起点0到i点的距离,c0j表示起点0到j点的距离,cij表示i点到j点的距离。
3.2 C-W节约算法的主要步骤
(1)将所有点排序,起始处所属的点为0点对应快递公司A,其他点任意排序,选取点0为基点,将基点与其他各点连接。(2)构建可连接点对S(i,j),按公式S(i,j)=c1i+c1j-cij计算各点对的节约值。(3)将所有点对S(i,j)按其值大小由大到小排列。(4)从节约值最大的点对开始依次向下构建路线,满足点i和点j不在一条路线上和点i和点j均为基点相邻这两个条件即可将点对纳入路线,否则舍去。(5)通过以上各迭代步骤,考察完所有点对,达到路径配送优化的目的。
4 论证分析
假设A为一家快递公司,其快递员每天都会对其公司的顾客进行上门取件送件。本文对该快递公司进行论证分析,选取该公司配送范围附近的6个客户作为研究对象。目前该公司采取的是门到门一对一的配送方式,即直接由该快递公司向客户点进行配送。这里所有客户之间的路线都是连通的,总是可达的,对于不连通的情况不是本文考虑范畴。对此,我们采用C-W节约算法来进行求解并与不采用C-W节约算法进行求解来进行对比。
4.1 建立模型
第一步:已知将6个客户点分别设为B、C、D、E、F、G,假设快递公司和6个客户之间的距离已知,如表1所示。
第二步:根据表1画出TSP问题的模型图,如图1所示。
4.2 算法求解
4.2.1 未选用C-W节约算法求解上述问题模型
如果不采用C-W节约算法进行求解,在本案例中我们要送达6个客户,从快递公司A出发,最后回到快递公司A。显然,从快递公司A出来后,我们随即可以选择6个客户之一进行快递的送取,那么很显然这里就有6种选择,分别为B、C、D、E、F、G。则此时可能的路线为:A→B,A→C,A→D,A→E,A→F,A→G.在进行第一次客户的选择后我们又可以从剩余的5个客户中进行选择,此时又有5种选择,也就是说此时就有5×6=30条路线,以此类推,下一次就有4种选择,将会产生5×6×4=120条路线。经过计算,本案例中的可选路线数为6!=720条,也就是说首先需要找出的这720条路线的过程就是非常复杂的,然而为了筛选出最短的那条路线,还需要计算出每一条路线的路径距离进行比较。这无疑是困难的,这仅仅只是送达到6个客户手中,如果是更多的客户则其路线便会更加复杂,就算利用计算机来计算,所耗费的时间也是很长的。
4.2.2 选用C-W节约算法来分析和求解上述的问题模型
选用C-W节约算法来分析和求解上述问题模型的具体步骤为:
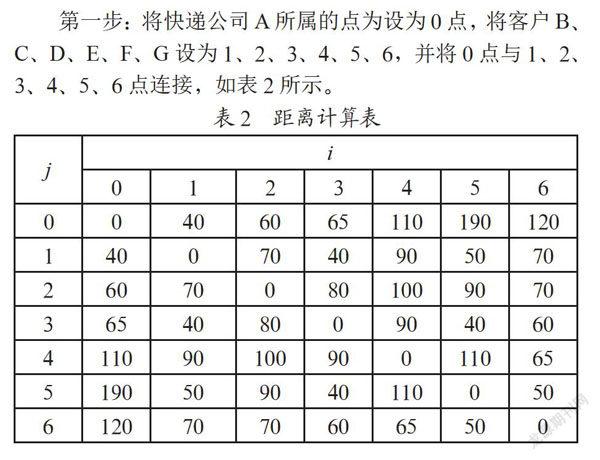
第一步:将快递公司A所属的点为设为0点,将客户B、C、D、E、F、G设为1、2、3、4、5、6,并将0点与1、2、3、4、5、6点连接,如表2所示。
第二步:构建可连接点对S(i,j),按公式S(i,j)=c1i+c1j-cij计算各点对的节约值并以节约值从大到小排序,如表3所示。
第三步:按照表2所示的节约值排序表,从节约值最大的点对开始依次向下构建路线。首先把节约值最大的构成回路,根据表2,节约值最大的是连接为5、6点对应的客户为F、G即连接0-5-6-0构成第一个回路,在剩下的节约值中最大的为连接3、5点构成回路,此时路线为0-3-5-6-0,按照上述方法下一步连接的应为4-5,但是5点所对应的客户已经与3点和6点所对应的客户构成回路且节约值都要大于s(4,5)点对,因此舍弃4-5回路。下一个1-5回路也是同样的道理,所以被舍弃。到4、6回路后可以和6回路进行连接中间没有别的客户,因此可以连接,此时的路线为0-3-5-6-4-0。以此类推,经过迭代舍弃了s(2,5)、s(3,6)、s(2,6)、s(1,6)、s(3,4)所構成的回路,与点对s(2,4)、s(1,3)构成回路形成最终路线为:0-1-3-5-6-4-2-0即从配送中心4出发先向客户B配送,再向客户D配送,在前向客户F进行配送,再从客户F到客户G,到客户E,再到客户C最后回到配送中心A。该线路的路程总和为:S=40+40+40+50+65+100+60=395
未优化前,该快递公司采用的是一对一的优化方式,耗时耗力总配送里程为S=2×(40+60+65+110+190+120)= 1 170,优化后与优化前相比节约了775,提高了配送效率,也节约了配送成本。
5 结 论
本文对快递配送的问题进行分析,通过模型的构建和算法的应用对配送的路径进行了优化,缩短了配送路线的距离,节约了配送成本,对于快递公司降低成本具有一定意义。但本文的研究还有一些不足,对于论证的条件过于理想化,在实际配送中要考虑的因素会十分复杂,对于这一方面还待与加强研究。
参考文献:
[1] 杨粟涵,于蕾.基于遗传算法的快递配送路径优化问题研究 [J].现代信息科技,2020,4(9):99-100+103.
[2] 邓学平,孙芹,田帅辉.基于不同车型的城市快递配送车辆路径优化研究 [J].价值工程,2020,39(12):275-280.
[3] 李瑞吉.城市末端快递配送现状及配送模式研究 [J].南方农机,2019,50(22):215-216.
[4] 蔺士文,杨金云,吴昊龙,等.基于节约里程法的物流配送低碳路径优化 [J].物流工程与管理,2019,41(4):80-82.
[5] 都雪静,孙菲菲,王云浩.小件快递配送路径优化研究 [J].物流技术,2018,37(4):29-35+40.
[6] 叶润舟.基于改进混合粒子群算法的快递最后一公里配送优化 [D].合肥:合肥工业大学,2019.
[7] 陈先受.众包模式下快递企业末端配送路径优化研究 [D].杭州:浙江工商大学,2018.
[8] 谢伟.基于同城配送的快递配送路径优化及应用研究 [D].沈阳:东北大学,2018.
作者简介:时宇(2000—),女,汉族,辽宁大连人,本科在读,研究方向:物流管理。
