往复压缩机管路系统气固耦合振动特性研究

赵 杰，姚 冉，王雯昕，周 晶，王博阳

（北京石油化工学院 机械工程学院，北京 102617）

0 引言

在石化生产中往复压缩机及其管路系统应用广泛，但往复压缩机呈间歇性与周期性吸排气流工作特性不可避免会发生振动，管路系统振动问题成为企业安全生产的一个重大威胁。管线剧烈振动会导致管道破裂、管道介质泄漏而引起爆炸、火灾等危险事故，不仅影响到企业的生产制造及经济效益甚至会触及到工作人员的生命安全，而美国每年因管线振动而造成的经济损失高达上百亿美元［1-13］。

以往的管路振动原因研究中会忽略管路系统本身和输送流体之间的耦合作用，LIANG等［14］从模态分析、共振管道长度计算、速度频谱分析、压力脉动测量等方面对某增压站调试过程中往复压缩机进口管道出现异常振动原因进行分析，结果表明进口管道上的大压力脉动和共振是引起振动的关键因素，但在该研究过程中没有考虑流固耦合作用对往复式压缩机进口管道出现异常振动的影响。严幼玲［15］在利用数值模拟法研究大型往复压缩机工作特性及管道气流脉动时，也没有考虑流固耦合作用的影响。而PEROV等［16］研究表明：结构单元和流体单元之间的耦合方法对特征频率的精度有重要影响，因此仅仅得到管路自身的固有频率虽可以解决大部分工程问题但研究结果还不够精确。朱竑祯等［17］采用理论计算和数值仿真互为验证的方法研究功能梯度输流管道振动问题时，考虑了流体与管壁的单向耦合作用。LEE等［18］研究表明：同时考虑机械力和流体力作用的管道振动预测结果与试验数据吻合较好，但并没给出预测趋势。张春晋等［19］采用数值计算研究管道车振动运移水力特性时，结果表明：考虑流固耦合下模拟值与试验值基本吻合，且相对误差不超过4.8%。综上，在预测管道振动时应考虑流体和固体的相互作用对管道振动的影响更接近工程实际。

流固耦合方法有单向流固耦合和双向流固耦合两种方法，但单向流固耦合将结构与流体视为单独个体仿真计算结果不如双向流固耦合准确［20-22］。赵杰等［23］基于气固耦合理论对管道充气前后（内压为300 MPa）振动进行数值模拟分析，分析结果表明：气固耦合作用对管段固有频率有影响，且变化在1.5%以内。王莹［24］在基于气固耦合研究介质压力（0.008，0.08，0.8，8，80 MPa）对往复压缩机管道固有频率的影响时表明：当工作压力为0.8 MPa以下前三阶固有频率变化率不超过2%；当工作压力为8 MPa前三阶固有频率变化率最高达12.6%；当工作压力为80 MPa，充气管第二阶固有频率比空管固频增加了62.6%。郭长虹等［25］利用有限元软件ADINA研究不同气体压力（0.3，0.5，0.7，1 MPa）对页岩气井下开采管路气固耦合振动特性的影响，研究结果表明：随着管路内气体压力的增加，管路固有频率降低。曹源［26］基于气固耦合管路动力学模型和振动数学模型，利用有限元软件ADINA研究不同压力（0.1，0.2，0.3 MPa）对气固耦合管路固有频率的影响。研究结果表明：工作压力在0.1～0.3 MPa气固耦合管路固有频率影响较小，但未研究更高工作压力气固耦合管路固有频率影响。马青等［27］以采空区埋地管线系统为研究对象，利用Hamilton原理研究天然气压力在1.5～6 MPa对输气管道固有频率的影响，结果表明：管道固有频率随流体压力的增加而降低。此外，雷太斌等［28-29］也研究了输气管道气固耦合振动特性。吴天新等［30］指出在气体钻井钻柱内注入高压气体的过程中，钻柱一直处于复杂的纵向与横向振动状态。孟庆华等［31-37］还研究了在不同气体流速下对结构气固耦合振动的动力特性影响。大部分学者们研究表明：气体在低压下结构的流固耦合特性问题是可以忽略的，但当气体处于中高压工作状态下结构的流固耦合问题是否可以忽略是未知的。因此，本文以往复压缩机管路系统为研究对象，基于往复压缩机管路系统双向流固耦合理论基础对往复压缩机管路系统进行模态分析、谐响应分析预测管路系统振动响应，并与试验数据进行对比验证仿真研究方法的有效性和研究方法的可行性。为了探究不同工况下气固耦合对管道结构固有频率的影响，进行不同工况下的耦合作用对管线振动影响预测。

1 往复压缩机管路系统流固耦合分析理论

往复压缩机管路系统的双向流固耦合的数值模拟计算模型包括计算结构动力学模型（CSD）和计算流体力学模型（CFD），本文研究的往复压缩机管路系统内的流体为空气。

1.1 结构与流体模型理论

管路系统计算结构动力学的理论的守恒方程由牛顿第二定律推导得出：

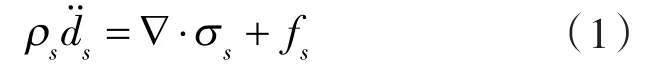
式中 ρs——管道材料的密度，ρs=7 820 kg/m；

σs——柯西应力张量；

fs——管道结构的体积力矢量。

管路内输送流体为空气，工作温度为25 ℃，通过查阅相关资料获得［38］，此时空气的黏度μ=18.488×10-6Pa·s，密度ρ =1.185 kg/m3，试验室内空气音速a=340 m/s，通过查看试验系统智能控制台获得管道内流体的质量流率q=0.003 kg/s，管道内径为d=0.045 m。

管道截面积A：

管道内流体流速v：

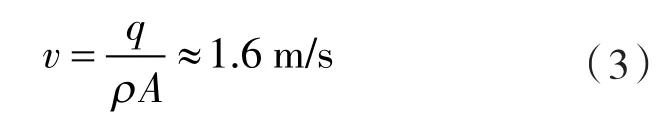
马赫数Ma：

说明往复压缩机管路内流体在该工况下为不可压缩流体。

雷诺数Re：

说明该工况下往复压缩机管路内流体不仅为不可压缩流体，也是充分发展的湍流模型。

因此，本文在对往复压缩机管路系统做流固耦合计算时，流体采用标准的k-ε模型。

管路内流体气动模型建立遵循质量和动量守恒定律，控制方程如式（6）、（7）所示。

质量守恒方程：

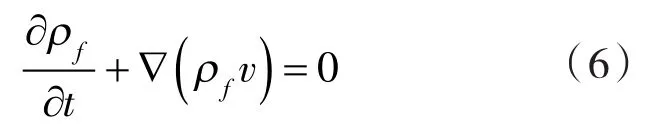
动量守恒方程：

式中 ρ ——空气的密度，ρ=C（常数）；

t ——时间；

v ——空气速度矢量；

τf——空气的剪切应力张量；

ff——管道内空气的体积力矢量。

1.2 流固耦合理论

流固耦合相较于结构动力学、计算流体力学同样遵循最基本的守恒原则，即在往复压缩机管路系统流固耦合交界面上，满足应力和位移的守恒。

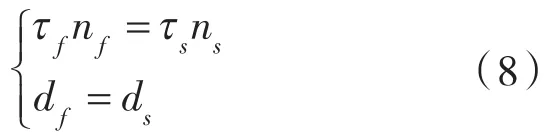
式中 nf——管道内空气的单位方向向量；

ns——管道结构的单位方向向量；

df——空气的位移；

ds——管道结构的位移。

2 振动原因分析

2.1 基于双向流固耦合的往复压缩机管路系统振动原因分析

2.1.1 模型建立

图1所示为试验系统的平面流程。本文以管线L5为仿真对象，研究在考虑流固耦合情况下往复压缩机管路系统振动超标问题，首先建立管道模型和管内流体模型，管道内径d=45 mm，外径D=60 mm，管道材料为结构钢，总长L=2 075 mm，有两个弯管，两个弯管之间的中心距h=165 mm，法兰采用D50型号，仿真模型如图2所示。然后建立L5管路的网格传递分析模型，采用多区域网格划分法进行管路结构的网格划分，共划分网格3 612个，管路内流体域采用inflation法对流固耦合面进行分层细化处理，将流固耦合交界面分为3层，其余均采用默认的自动划分网格，共划分网格93 119个，固体域和流体域网格结果如图3所示。

图1 平面流程Fig.1 Plane flow chart

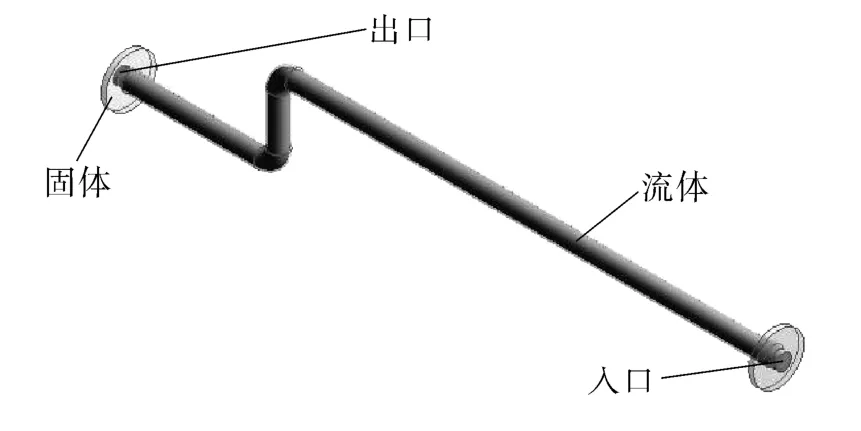
图2 仿真计算模型Fig.2 Simulation calculation model

图3 网格划分结果Fig.3 Results of grid division

2.1.2 流固耦合分析

基于瞬时动力学和流体力学的耦合计算，综合考虑柯朗数、计算时间和计算精度选取瞬态计算的步长为0.05 s；由第一节的流体计算，流体采用标准的k-ε模型；模拟结构壁面采用无滑移绝热边界条件，管路入口与出口边界条件如式（9）所示，Pinlet是管道入口处的压力，Poutlet是管道出口压力。

经过求解计算得到如图4所示流体的流速矢量，由图4可以看出管路在输送流体时流速会在管道弯管处发生突变，将流场分析结果导入静力学分析，耦合面的压力分布如图5所示。对管道的入口和出口进行两端固定的约束，求解获得管道结构变形应力。将求解获得的变形应力作为预应力导入模态分析中，分析流固耦合对管道结构固有频率的影响。

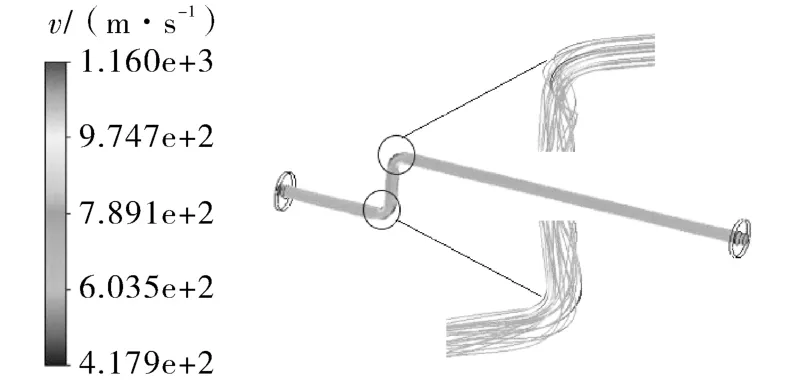
图4 流固耦合分析结果Fig.4 Graph of fluid-solid coupling analysis results

图5 耦合面的压力分布Fig.5 Pressure distribution of the coupling surface

2.1.3 模态分析

为精确分析双向流固耦合对往复压缩机管路系统振动影响，仿真分析了流固耦合状态下和非流固耦合状态下往复压缩机管道振动响应。考虑流固耦合状态下，将双向流固耦合分析获得流固耦合面上的应力值作为管道的预紧力，边界条件采用出入口处两端固定的约束条件分析往复压缩机管路振动原因；不考虑流固耦合状态下，只施加边界条件对管路系统振动超标进行仿真分析。

管线耦合和非耦合作用下的前10阶固有频率对比见表1，通过对比有、无耦合对固有频率的影响得出：0.6 MPa的工况下流固耦合作用对管道固有频率的影响总体上可以忽略，只对第一阶固有频率会有大约12.9%的相差百分比。且随着固有频率阶数的增加，考虑耦合作用和不考虑耦合作用下管道固有频率的变化及其振型趋势基本相同，最大变形位置大致相同，但耦合作用下管道的各阶振型最大变形量也更高，图6所示的第三阶振型对比所示即可体现。

图6 耦合与非耦合作用下第3阶振型对比Fig.6 Comparison of third-order modes under coupled and uncoupled action

表1 管线耦合和非耦合作用下的前10阶固有频率对比Tab.1 comparison of the first ten natural frequencies of the coupled and uncoupled pipelines

2.1.4 谐响应分析

试验台研究往复压缩机的转数N=340 r/min，双缸作用m=2，往复式压缩机激发主频率f=Nm/60=11.3 Hz，因此，在谐响应分析中管道的激发频率 fn=11.3n（n=1，2，3，…）。

在对管道进行谐响应分析时，研究管道在50倍往复式压缩机工作频率下的振动特性，仿真求解计算获得耦合和非耦合作用下的频率响应位移曲线如图7所示。由图7可以看出，耦合和非耦合作用下管道振动频率响应在101.7 Hz（9倍频）和361.6 Hz（32倍频）时出现变形位移峰值，但在研究管线振动是否是由共振引起只考虑前10倍频作用。因此，在361.6 Hz（32倍频）时出现管道振动频率响应变形位移峰值可以剔除，图8所示为管道在101.7 Hz（9倍频）时出现管道振动频率响应的变形位移，结合图7和8可以看出，耦合和非耦合作用下发生共振的倍频是相同的，最大变形量的位置相同，但耦合作用下频率响应振动位移大于非耦合作用下的振动位移，耦合作用下最大变形位移约为0.385 mm，非耦合作用下约为0.166 mm。

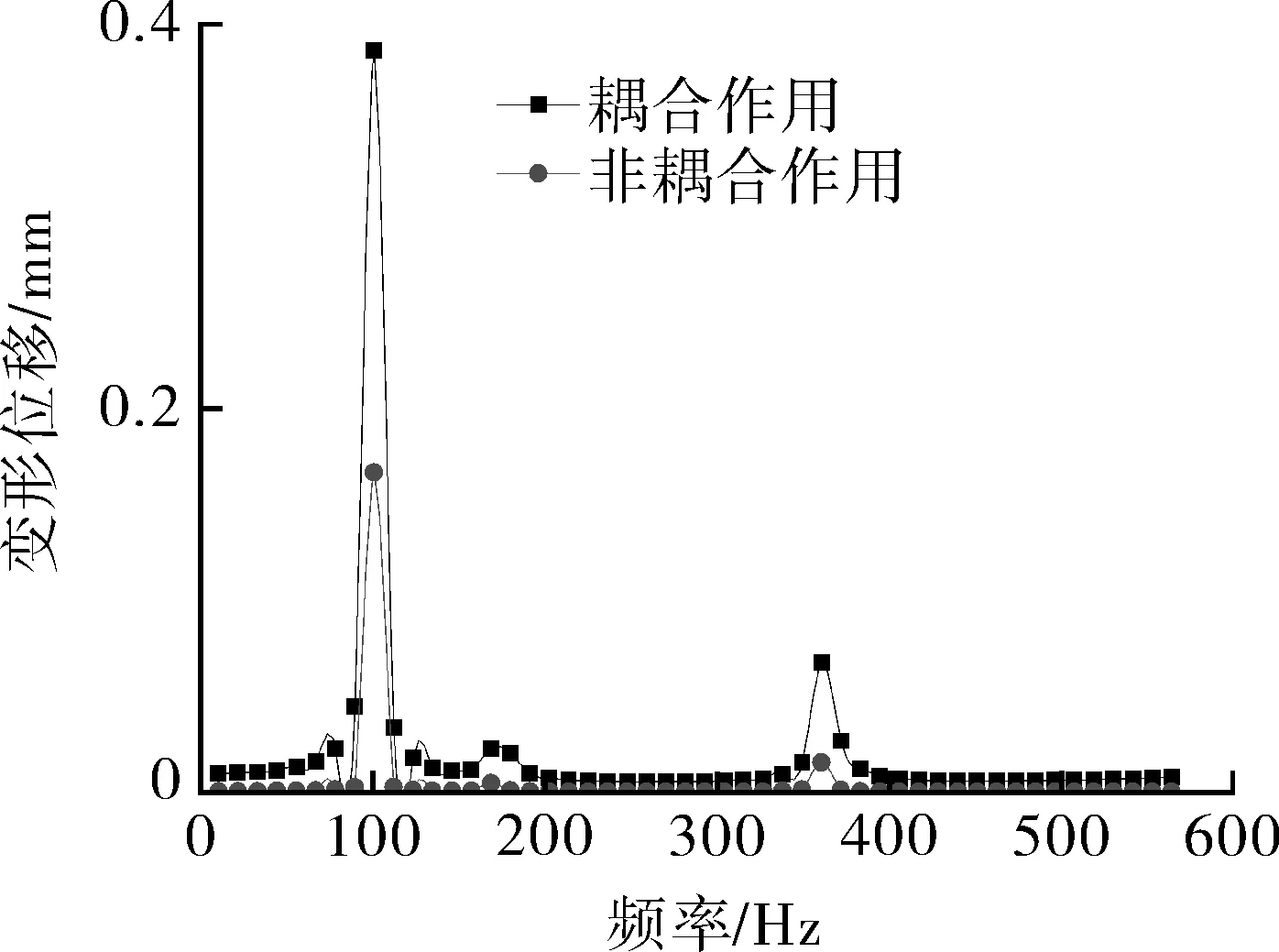
图7 耦合与非耦合作用下管路的频率响应振动位移对比Fig.7 Comparison of inherent frequencies of the first ten orders under the coupled and uncoupled action of the pipelines

图8 耦合与非耦合作用下9倍频作用下管道的变形位移云图对比Fig.8 Comparison of deformation displacement nephograms of pipeline under 9 octave frequency under coupled and uncoupled action

2.2 试验验证

由图1可知，以管线L5上分布的振动测点1，2，3为例，采用上海某公司的ZD-700无线振动传感器获得往复压缩机管线系统在正常工作下测点1，2，3的振动响应数据，见表2。根据美国普渡压缩机协会管道振动要求，管线振动评价标准中振动位移介乎设计与修改之间的界限为≤240 mm，修改界限为≤470 mm。

表2 试验测量数据Tab.2 Experimental measurement data μm

由表2可知，测点1和2的振动响应位移已经超过了美国普渡压缩机协会管道振动要求中介乎设计与修改之间的界限。结合仿真分析中往复压缩机管路系统考虑耦合作用和非耦合作用下振动响应预测，在考虑耦合作用下的9倍频处出现的振动位移响应出现的峰值与试验测量数据更贴近（耦合作用误差率为9.8%，非耦合作用的误差率为52.5%）。因此，试验台往复式压缩机振动超标的原因为共振，同时验证了本文仿真研究往复压缩机管线振动技术的可靠性和合理性，同时验证了在考虑耦合作用下研究往复式压缩机管线振动超标原因更精确。

3 基于双向流固耦合对不同工况下管路固有频率影响的预测

为进一步探究在考虑耦合作用的情况下不同工况是否会改变管道结构的固有频率，在原有仿真路线上通过改变管线的工作压力来预测管线固有频率的变化。预测往复式压缩机管路系统工作压力的研究值为：0.6，6，60，100，150，180，195，200，230，260，280，300 MPa，不同工况对管道前10阶固有频率影响如图9所示。由图9可以看出，工作压力在0.6～195 MPa之间，管道前10阶固有频率处于相对平稳阶段即：随着管道工作压力的增加，管道固有频率基本不会发生变化；工作压力在195～300 MPa之间，随着工作压力的增加，管道前10阶固有频率处于上升阶段即：管道的固有频率总体上随着工作压力的增加而增加。这是由于随着压缩机工作压力升高空气的密度也会随之增加，当工作压力为200 MPa时，空气的密度高达2 828.36 kg/m3（相当于纯铝的密度）。因此，当管线系统的工作压力处于高压或者超高压状态时就需要考虑流固耦合作用对管线结构固有频率的影响。

图9 不同工况下管道前10阶固有频率变化对比Fig.9 Comparison of inherent frequency variation of the first 10 orders of pipeline under different working conditions

4 结论

（1）以瞬时动力学和流体力学理论支撑本文仿真研究（气固耦合分析、模态分析、谐响应分析）往复式压缩机管路振动超标是合理的。

（2）考虑流固耦合作用的往复压缩机管线振动响应预测结果更接近于试验台测量数值，耦合作用下的误差值仅为9.8%，非耦合作用的误差率为52.5%；结合美国普渡压缩机协会管道振动标准确定了试验台管线振动超标的主要原因是在2阶9倍频处发生共振。

（3）通过试验与仿真互为验证的方法确定了本文仿真路线的有效性与可行性；在原有仿真路线的基础上预测了0.6～300 MPa工况下管道固有频率的变化，预测结果表明：随着管道工作压力的增加，管道固有频率变化分为平稳区（0.6～195 MPa）和上升区（195～300 MPa）这两个区，因此当管线工况处于高压和超高压时流固耦合作用是不可以忽略的，而在平稳区虽可以忽略耦合作用对管线固有频率的影响，但研究管线的振动位移响应时会存在误差。