多级降压调节阀阀芯流阻特性及参数分析

2021-02-16邓建飞寇琳媛金鹏飞朱学军马玉山

流体机械 2021年12期

王冠，邓建飞，寇琳媛，金鹏飞，朱学军，马玉山

（1.宁夏大学机械工程学院，银川 750000；2.宁夏大学宁夏智能装备 CAE 重点实验室，银川 750021；3.吴忠仪表有限责任公司，宁夏吴忠 751100）

0 引言

随着节能减排工程的发展，高压减压阀在工程领域得到了广泛的应用［1-3］。其中多级减压调节阀以流量控制稳定，耐高压等优点广泛地应用在各种工业系统中［4-5］。多级降压节流元件是多级降压调节阀关键控压结构，其流道窄而压力大，对其进行结构改进以适应工程领域严苛的工作条件、延长使用寿命对工程领域有重要意义。

目前，降压性能一直是调节阀研究的热点，围绕实际工程问题，众多学者对调节阀降压结构开展了深入的研究工作。侯聪伟等［6］对高压减压阀进行了参数化分析，分析了相对角度、孔板厚度、孔板数量和板孔直径对多级降压调节阀的控制性能的影响，结果表明相对角设为时，蒸汽流经多孔带冠阀芯，可以获得最大的减压压力，紊流度最低。高佳男等［7］针对气体低压中小口径管道流量调节，设计了一种新的轴流式流量调节阀，同时采用计算流体力学（CFD）方法对所设计的调节阀内部流动和流量调节特性进行了仿真分析，得到流量特性曲线，结果表明，所设计的调节阀流量调节特性与设计曲线相符。黄凯等［8］基于标准K-ε湍流模型对四组不同阀芯结构（平底、小弧、大弧、波浪形）调节阀流阻性能进行研究，发现大弧形与波浪形阀芯结构调节阀的截阻性能较平底阀芯调节阀的流阻系数值减小9.71%，同时阀芯处于全开度时，平底阀芯截阻性能具有一定的优势。姚世卫等［9］利用FLUENT流体计算仿真软件对不同开度时阀口的流量特性进行了数值模拟，并通过试验对阀口的流量特性进行了验证。

众多学者通过计算流体力学的方法对阀门的内部流场进行了数值模拟分析研究。宋学官等［10］建立了直接操作安全泄压阀（SRV）精确的CFD模型，模拟了系统从阀门开启到关闭的全过程，得到了可压缩流体通过SRV的详细图像，包括阀座区域的小尺度流动特征。钱金元等［11］研究了新型高压减压阀（HPRV）及其连接管道内多级多孔板的马赫数，分析了可逆等熵过程的马赫数，提出了HPRV多级多孔板的设计方法，并进行了数值模拟。NIKO HERAKOVIČ 等［12］基于数值模拟和实验分析，提出改变阀室和阀芯的几何形状，可以显著降低流体力的轴向分量，从而降低必要的驱动力。YOUNG JOON AN等［13］利用CFD方法对LNG船用系统抗汽蚀控制阀进行了三维不可压缩湍流流动的数值分析，研究和分析了具有复杂流场的调节阀的流动特性，通过CFD分析显示出改进的流型，减少了汽蚀。

通过对以上文献进行分析可以知道降压结构对阀门控制性能起决定性作用，然而具体针对多级减压阀降压结构部分进行结构优化和分析的文献较少。本文通过数值模拟，分析串式多级降压调节阀阀芯的流量特性，以及研究不同降压阀芯参数（转弯倒角和流道倾角）对内部流场的影响。为改善节流元件的节流效果提供理论依据，对其他串式多级降压调节阀设计也有一定的借鉴意义。

1 数值计算方法

1.1 控制方程与湍流模型

流体控制方程与湍流模型对内部流场数值模拟分析有重要影响。在分析多级降压阀内部流动时，首先要求解质量守恒方程和动量守恒方程，此外，在进行流阻特性分析时应考虑流量系数以及流阻系数方程。

连续性方程：

动量方程：

流量系数：

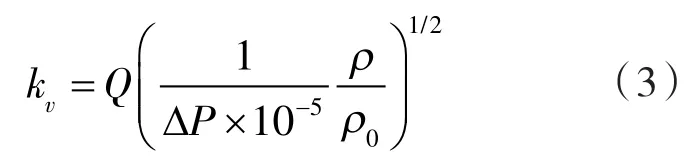
流阻系数：

式中 v ——运动黏度；

Q —— 流量，m3/h，Q=Avin；

A——管道横截面积，m2；

vin——管道进口流速，m/s；

ρ ——对应的介质密度，kg/m3；

ρ0—— 15 ℃时水的密度，kg/m3，其中ρ0=999 kg/m3；

ΔP —— 阀前后压差，Pa；

va——阀门平均流速，m/s。

通过多级降压调节阀阀内介质的流动状态为湍流流动，因为雷诺数数值大于106。RNG K-ε湍流模型与标准k-ε模型相似，考虑了涡流对湍流的影响，提高了涡流计算精度，同时RNG K-ε湍流模型被证明能更准确地描述高压降压阀内部的复杂流动［10-24］，因此本次数值模拟采用RNG K-ε湍流模型，其对应的湍动能K和湍流耗散率ε方程如下：

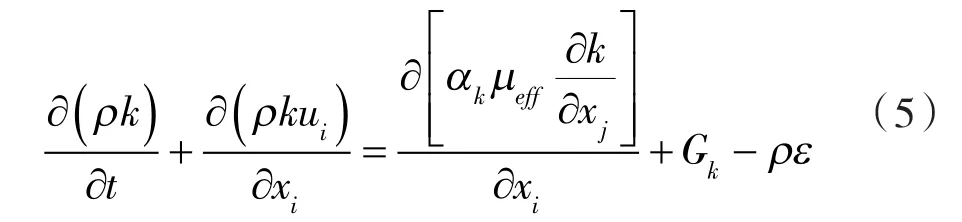
其中Rε为：

有效湍流黏度 μeあ为：

式中 Gk—— 由平均速度梯度引起的湍动能生成项；

其中经验常数αk= αε=1.393，Cε=1.68；经验常数修正值 C1ε=1.42；Cμ=0.084 5；η =SK/ε，η0=4.38，β=0.012。

1.2 几何结构与计算模型

图1（a）示出串式多级降压调节阀的结构，主要部件包括阀体、阀芯、阀芯套、阀杆等。其中流体流向为左进右出，流体介质从阀芯底部的凹口流入阀门降压结构，从阀芯套上顶端4个圆孔流出，完成对流体的降压，主要降压区域为阀芯与阀芯套组成的降压结构，如图1（b）所示，降压结构由3个凹口以及出口组成，每个凹口由四级降压结构组成，包括转弯和流道倾角部分，如图1（c）所示。

图1 串式多级降压阀结构及流道示意Fig.1 Schematic diagram of structure and flow channel of the tandem multistage step-down valve

由于本次数值模拟只对阀芯降压结构部分进行参数化分析，故只对阀芯流道部分建模，即阀芯与阀芯套组成的降压结构部分，其结构如图1（b）所示。图1（c）示出多级降压调节阀的每一级凹口流道，对图1（c）所示的降压结构建立不同参数的降压结构流道模型，参数包括转弯倒角L和流道倾角θ。

表1为多级降压调节阀阀芯结构参数，建立不同参数的流道模型，分析参数对流体流动的影响，并建立不同开度的流道模型，以分析其流阻特性。参数分析中流道倒角为 2，4，6，8，10 mm，倾角为36°，48°，60°，72°。在进行倾角分析时，倒角均设置为0 mm，进行倒角分析时，倾角均设置为48°。

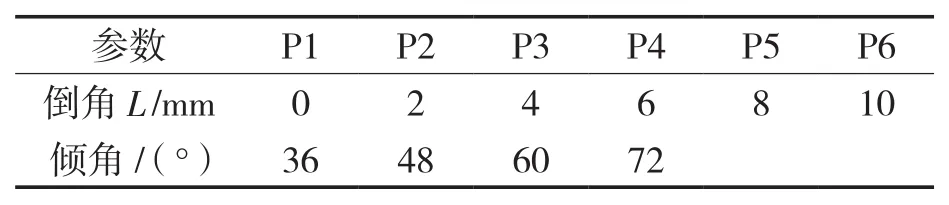
表1 流道的参数分析Tab.1 Analysis of flow channel parameters

1.3 边界条件和网格无关性

阀门中的流体介质是渣油加氢装置中的热高分油。边界条件采用压力进口和压力出口。进口压力为18.7 MPa，出口压力为2.9 MPa，流体介质密度为 680.9 kg/m3，动力黏度为 1.4×10-4kg/ms。由于结构的对称性，用实际流场的一半进行计算，对称中心平面作为对称面，其他表面均设置为光滑无滑移壁面。

网格划分时，网格质量和网格大小均是影响计算精度的重要条件。采用ANSYS mesh划分网格，因为降压结构部分的复杂性，所以采用自动网格划分的方式进行网格划分。在数值模拟之前，需要对网格进行独立性检验。通过改变单元尺寸的大小，调整计算区域的网格数目，得到合适的网格划分。选择原结构进行网格独立性检验，如图2所示，在网格尺寸为1.5 mm和1 mm时，出口的质量流量相对误差为0.05%，故认为可以进行数值模拟。由于考虑到降压结构部分的复杂性，所以本次数值模拟采用网格大小为1 mm进行计算。

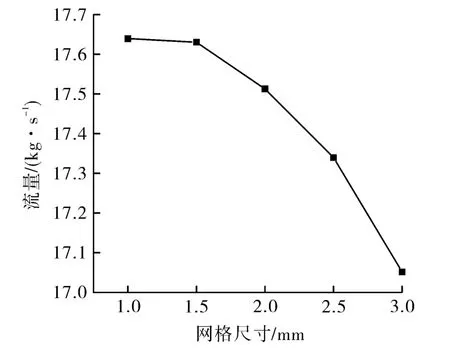
图2 网格无关性验证Fig.2 Grid independence verification

2 结果与分析

2.1 流量特性

对不同开度下阀芯的流道结构，分析其流动特性。基于不同开度的稳态仿真结果，分别做出流量系数和流阻系数的特性曲线，如图3，4所示。从图3，4中可以看出，随着开度的变化，流量系数和流阻系数有着相反的变化趋势，流量系数随着开度的增大而增大，流阻系数随着开度的增大而减小，这一变化也可以从理论公式推导得出，将流量系数和流阻系数公式联立得：

图3 流量系数特性曲线Fig.3 Characteristic curve of flow coefficient

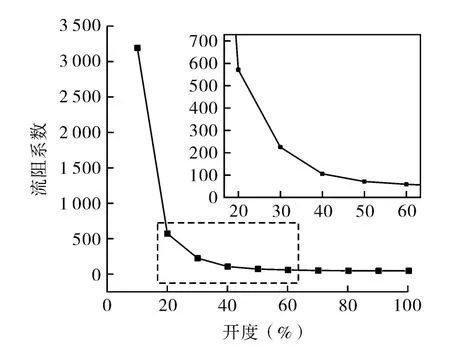
图4 流阻系数特性曲线Fig.4 Characteristic curve of flow resistance coefficient

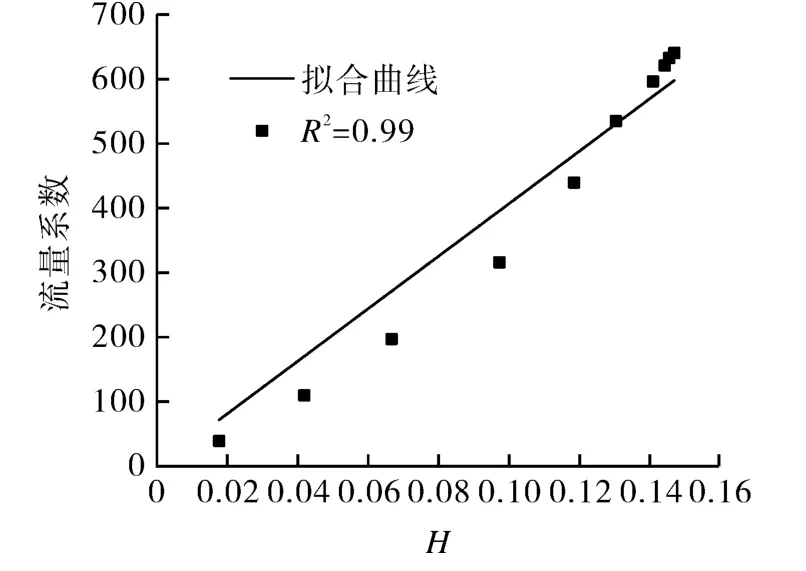
图5 流量系数与流阻系数关系曲线Fig.5 Relation curve of flow coefficient and flow resistance coefficient

从图3，4还可以看出，多级降压调节阀在中小开度下有较好的线性流量特性，随着开度的增大，在开度达到80%之后，开度继续增大，其流动阻力变化不大，因此对应的流量系数变化较小。对于流阻系数，开度在40%之前，因其阀芯和阀芯套的结构特点，随着开度的增大，流阻系数迅速减小，在40%开度以上时，流阻系数变化不明显。

从单级流道示意图中可以看出流道的降压部分主要由转弯和拐角组成，为了在高压差等恶劣工况下获得更好的减压过程，研究不同结构参数对其内部流动特性的影响。主要研究节流元件的结构参数，有流道倾角和流道倒角两部分。

2.2 流道倾角对流体流动的影响

流道倾角会改变流体在流道中的流动状态。因此，针对流道倾角对流体在多级降压结构中内部流动的影响开展研究。

图6示出不同流道倾角对称平面内的压力分布。当流体进入节流结构时，其流动截面迅速收缩。此时流体速度增加，压力降低。根据能量守恒定律，流体在节流结构中流动时，由于弯道近壁面会形成涡流，从而造成能量的消耗，压力无法回到原来的值。从图中可以看出，当流道倾角小于48°时，近壁面的涡流区明显增大；当流道倾角大于48°时，随着流道倾角的增大，近壁面的涡流区明显减小。

图6 不同流道倾角对称面压力分布Fig.6 Pressure distribution on symmetrical surfaces with different flow channel inclination angles

图7示出不同角度X方向上的压力分布。从压力分布图中可以看出，节流结构对流体的整体压降达到逐级降压的效果。流道倾角从36°变化到72°时，节流结构内的流动阻力不同，压降也发生变化。其中，当x=0.08 m时，流道倾角越大，第一凹口的压降越大，且此后每级凹口都表现出相同的变化趋势，即流道倾角越大，每一级凹口分配的压降越大，在流道倾角为72°时，每一凹口的压降达到最大，在凹口处完成主要降压，从而使得在出口处压降减小，进而能减小在出口处产生空化的概率。同时，由图可知，随着流道倾角的增加，在每一凹口处，压力恢复逐渐增大，当流道倾角为48°时每一凹口的压力恢复没有另外3个角度时剧烈，且压降比较平稳。

图7 不同角度X方向压力分布示意Fig.7 Schematic diagram of pressure distribution in X direction at different angles

在不同流道倾角的情况下，多级降压阀节流结构内部速度、湍流动能和湍流耗散率的最大差值见表2。从表中可以看出，倾角在48°时，速度、湍流动能和湍流耗散率的最大差值均为最小值，由以上可以确定的是，倾角在48°时为最佳的流道倾角值。

表2 不同流道倾角的速度和湍流参数最大差值Tab.2 Maximum difference values of velocity and turbulence parameters with different channel inclination angles

2.3 流道倒角对流体流动的影响

倒角的目的是将直线过渡变为平滑过渡。与直线过渡相比，平滑过渡可以使拐角处的流体流动更加均匀，湍流强度更小，因此倒角可以帮助改变多级降压调节阀内部的流体流动状态。倒角参数分析为从0 mm增加到10 mm，以2 mm为间隔，分别分析其对多级降压调节阀内流体流动的影响。

图8示出不同倒角长度对称面单级凹口速度分布。由图可知，随着倒角的增大，流道近壁面的涡旋区域在逐渐减小，但是却在流道倒角处形成了高速射流，其最大速度分别为100.11，124.31，124.01，129.04，121.56，127.17 m/s。随着倒角的增大，流道倒角处射流区域在逐渐增大，这是因为随着倒角的增大，流体进入倒角部分的缓冲区域减少，在倒角部分造成的压力损失减小，因此导致射流区域逐渐增大。

图8 不同倒角长度对称面单级凹口速度分布Fig.8 Velocity distribution of single notch on symmetrical planes of different chamfered lengths

图9示出了不同倒角出口处的平均速度，从图中可以看出，随着倒角的逐渐增大，出口处的平均速度在逐渐减小，且近似呈线性关系，经线性拟合得到：

图9 不同倒角出口处的平均速度曲线Fig.9 Average velocity curves at different chamfer exits

式中 v ——出口的平均速度，m/s；

L ——倒角的长度，mm。

从拟合公式可知：随着倒角的增大，出口处的平均速度在呈线性关系的减小。

图10示出了不同倒角长度下多级降压调节阀阀芯内部湍流动能和湍流耗散率的最大差值。

图10 湍流参数最大差值曲线Fig.10 Maximum difference curve of turbulence parameters

从图中可以看出，在流道倒角为6 mm时阀芯内部湍流动能和湍流耗散率的最大差值均为最小值，分别为 28.86，831 511.1 m2/s2，其中倒角设置为6 mm时，相对于倒角为0 mm时，平均湍动能降低73%，极大程度的降低了流体介质的湍流度。倒角在8 mm和10 mm时湍流动能和湍流耗散率突然增大是因为倒角增大，导致流体在倒角处速度的急剧增加，形成高速射流，使得流体湍流程度变得非常剧烈。图11示出不同倒角时湍动能平均值与均方差对比，其中均方差用来衡量一组数据的离散程度的统计量。由图11可知，在横坐标方向上，不同倒角的湍动能平均值差异不是很大，在纵坐标方向上，可以看出，均方差与平均值的差异，即数据的偏离程度，也代表了湍动能的偏离程度，其差值越大表明湍流强度越强，也即流体流动状态更不稳定。从图10，11曲线变化可知，倒角对流体内部流动有很大影响，这是因为倒角可以帮助改变多级降压结构内部的流体流动状态，适当的倒角可以使得流体流动时更加平缓。

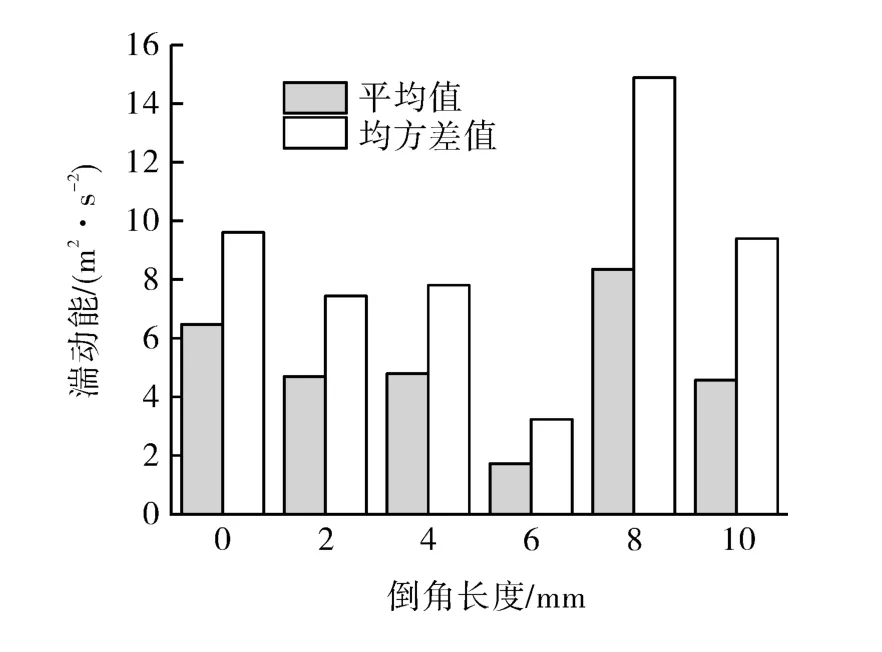
图11 不同倒角湍动能平均值与均方差对比Fig.11 Comparison of mean and variance of turbulent kinetic energy with different chamfer angles

图12示出不同凹口及出口压比曲线。从图中可以看出，随着流道倒角的增加，凹口处压降在逐渐增大，出口处压降在逐渐减小，且流道内的压降在同一凹口时，倒角越大，压降越大，说明倒角对流道压降分布有显著的影响。在第一凹口时，倒角从下到上的降压顺序为 0，2，4，6，8，10 mm分布，分别为21%，25%，25%，26%，26%，28%，以上可知，在第一级凹口时，压降均没有超过30%，同理可知，在第2和3级凹口时，均有倒角越大，压降越大，且压降均分布在30%附近，所以在出口处，倒角越大，压降越小，其从下到上的排列顺序为 10，8，6，2，4和 0 mm，压比分别为 10%，13%，15%，18%，19%和20%，出口处压降2 mm比4 mm大是因为在第3级凹口时4 mm的压降小于2 mm压降。当在出口处压降很大时，会在出口处形成高速射流和发生汽蚀现象，从而冲击壁面，造成节流结构的破坏，而适当增加倒角则可以降低出口处分配的压降，从而减小发生汽蚀的概率。由以上可以得出结论存在一个最佳倒角值为6 mm，可以将内部湍流动能和湍流耗散率降到最低，同时更合理的分配压降，减小出口处发生汽蚀的概率。