环形间隙密封泄漏率计算方法研究
2021-02-16曹志康王旭华
胡 琼 ,肖 洋 ,卢 迪 ,曹志康 ,王旭华 ,王 衍
(1.江苏海洋大学 机械工程学院,江苏连云港 222005;2.南京航空航天大学 直升机传动技术重点实验室,南京 210016)
0 引言
旋转机械泄漏是整个机械行业的诟病,严重影响我国实体经济的发展。而环形间隙类密封因其结构简单、成本低、无摩擦磨损、无功率损失以及无转速和温度的限制,被广泛应用于各种设备的润滑与密封系统中[1-2],如设置在两个存在压差的区域之间。但使用该结构存在两个问题,一是间隙密封一般比接触式密封泄漏量大,造成油路压力损失较大,油量计算时若不考虑润滑油泄漏损失,则很可能导致后续旋转部件因润滑不良而损坏;二是如泵、压缩机、汽轮机及高速齿轮箱等设备的轴间密封[3-10],油路中的润滑油会从环形间隙泄漏到壳体内,泄漏量过多会增大设备泄漏风险。因此,确定环形间隙密封泄漏率的精确计算方法,有助于润滑油路总进油量准确计算,对油路的优化设计起重要作用,更重要的是为环形间隙类密封的设计计算提供一定的理论基础。
HUANG[11]通过建立二维和准一维的环形间隙密封流体模型,求解流体控制方程获得泄漏率。GOWDA等[12]利用有限元法求解含表面粗糙度因子的二维平均Reynolds方程,获得环形间隙密封的泄漏率。GAUTAM等[13]基于湍流润滑理论,考虑流体惯性效应,获得环形密封不可压缩湍流时的泄漏量计算方法。SAN等[14-15]通过设计复杂的试验对环形间隙密封的泄漏进行测量。然而这些方法或复杂或成本较高,不适于工程应用。针对此情况,本文将系统地总结现有环形间隙密封泄漏率理论计算方法,并与数值计算方法进行相互验证,同时对影响泄漏的重要因子进行分析,以为工程旋转机械的环形间隙密封提供准确而简单的计算方法。
1 几何模型及泄漏率理论计算基础
1.1 几何模型
环形间隙密封的密封原理可简单描述为:润滑油从高压侧流向低压侧,流动过程中因流体具有粘性,与壁面之间产生摩擦阻力,阻碍流体的流动,从而形成一道密封屏障。图1示出本文所研究的环形间隙密封的物理模型。其中,dm表示环形间隙平均直径;p1,p2表示间隙入口和出口处的压力;l表示间隙长度;h表示间隙宽度。

图1 零件间形成的环形间隙Fig.1 Annular clearance seal formed by parts
1.2 泄漏率理论计算基础
当不可压缩流体流过环形间隙时,构成间隙的两密封环相对静止和相对旋转时的理论计算方法有很多,但通常都基于如下计算式[16-18]:

式中 η ——动力黏度,Pa·s。
当间隙为普通环形间隙(图1)时,D=dm,综合膜厚H=h3/2。有资料显示,无论是否有转速,只要流动处于层流状态,转速对泄漏的影响均忽略不计,可基于式(1)进行计算[19-20]。因此,下文将重点阐述静止状态下的泄漏率计算问题。
2 数值方法和试验验证
2.1 数值方法
采用FLUENT软件开展数值计算,而网格质量对仿真分析至关重要,为保证仿真结果的准确性,首先对不同网格质量下的泄漏率进行对比,以获得使计算结果准确且节点数最少的网格划分方式,由于密封间隙为环形圆柱,故采用六面体结构化网格。本文计算模型为:间隙平均直径dm=199.5 mm,间隙宽度h=0.25 mm,间隙长度l=140 mm,1/1 800的周期模型。边界条件和设置见表1。间隙流体流动状态由雷诺数判断,计算方法[21]如下:
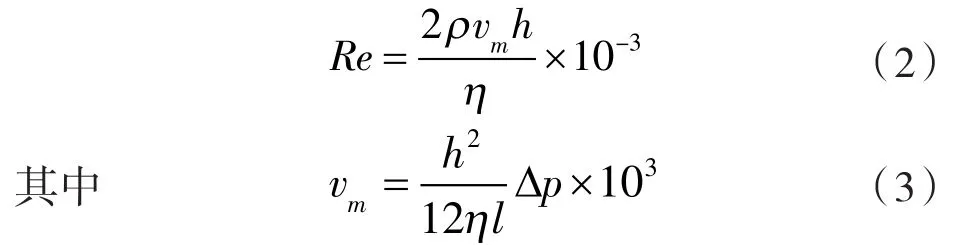
式中 ρ ——介质密度,kg/m3,ρ =905.65 kg/m3;
vm——间隙轴向平均流速[16],m/s;
η ——动力黏度,Pa·s,η =0.481 1 Pa·s。
当压差 Δp =0.3 MPa时,Re=0.022<<2 000,为层流。

表1 边界条件与数值方法Tab.1 Boundary conditions and numerical method
取无转速、压差Δp=0.1 MPa为计算工况进行网格无关性检验,结果如图2所示。图中标记点的横坐标值分别对应的液膜层数为1,2,3,4,5和6。结果显示:当节点数为151 254,液膜层数不小于4层,纵横比(Aspect ratio,即网格单元体最长边与最短边长度之比)在1~1.5时,每增加一层网格,泄漏率减小量不超过4%,因此取此时的网格参数进行后续的数值计算。

图2 网格无关性检验Fig.2 Grid independence test
2.2 数值方法的试验验证
本研究设计了一套环形间隙密封泄漏试验系统(如图3所示),可对静止条件下的泄漏率数值计算方法进行准确性验证。

图3 环形间隙密封测试系统Fig.3 Annular clearance seal testing system
图3示出的测试系统中的环形间隙密封试验装置为立式,密封间隙由密封腔、Ra0.63的内圆面和Ra12.5的外圆面组成,管路采用DN10的全新无缝钢管,间隙密封近进出口处分别设置精度为0.5%的NEXON PNS4000压力传感器和TNS3000温度传感器,调节油温T1=32±0.5 ℃,油压P1(0.15~0.4 MPa)。图中,T2和P2为常温常压,采用0.2%精度的均溪LE2科氏力质量流量计测量间隙密封泄漏量Q,将其与数值计算结果进行对比,结果如图4所示。由图可知,数值计算结果与试验结果吻合较好,二者差值随介质压力的增加而增大,但试验值略小于计算值,可能是因为管路中存在多处变截面,虽然改变量微小,但当介质压力增加,管路中的油液流动速度增大,与变截面的撞击越来越大,动能损耗增大;与此同时,油液中产生了更多的微小气泡,增大了流动阻力,而在数值计算时,并未考虑率空化现象;此外,表面粗糙度也许起到了一些作用,但间隙宽度与表面粗糙度比值大于3,因此影响微弱[22-23]。尽管如此,由对比结果可知,在所研究压力范围内,数值计算最大误差不超过8%,因此认为数值方法有效,可用其对环形间隙密封进行进一步计算分析。

图4 数值方法的试验验证Fig.4 Experiment validation of numerical method
3 重要的泄漏影响因子分析
3.1 表面粗糙度的影响
环形间隙泄漏阻力越大,泄漏率越小,因此分析表面粗糙度对泄漏率的影响,也可转化为分析表面粗糙度对间隙阻力的影响。间隙摩擦系数[2]计算方法如下:

当流动处于层流区(Re<2 000)时,可采用式(4)计算摩擦系数,当处于过渡区(2 000

图5 环形间隙摩擦系数λ与雷诺数Re及相对表面粗糙度ε/h的关系Fig.5 Relation of friction coefficientλof annular clearance with Reynolds number Re and relative roughness ε/h
3.2 轴向锥度的影响
存在轴向锥度时的间隙如图6所示,其中p1>p2,锥度定义为φ=(h1-h2)/l。静止时的泄漏率也采用式(1)计算,其中

图6 锥形间隙示意Fig.6 Schematic diagram of taper clearance
采用上述雷诺数判定法,间隙取平均间隙(h1+h2)/2,确定此情况下的间隙流动也为层流。对比不同锥度下的环形间隙泄漏率的理论与数值计算结果,以验证参数D和H表达式的正确性,且同时对h1>h2(收敛型间隙)和h1 表2 锥形间隙密封泄漏率模拟与理论计算结果对比Tab.2 Comparison between simulated and theoretical calculation results of leakage rate of tapered clearance seal 从表2可以看出,在平均间隙不变的情况下,泄漏率随着锥度的增大而减小。在静止时,收敛型和发散型间隙的密封效果几乎无差别,但理论结果明显小于仿真结果,将理论结果乘以系数2后(结果也列于表2),二者几乎完全吻合,故对H乘以系数2进行修正,修正后 文献[17]给出偏心时泄漏率Qe与无偏心时泄漏率Q0(由式(1)计算)的关系式为: 式中 e —— 偏心量(构成偏心环形间隙的两零件中心之间的距离),mm; h0——无偏心时的间隙宽度,mm。 此时对应的式(1)中,Q=Q0,H=h03。依据雷诺数计算结果,采用层流模型进行数值模拟验证,其对比结果如图7所示。 图7 偏心量对泄漏率的影响Fig.7 Influence of eccentricity on leakage rate 从图7中可以看出,环形间隙密封的泄漏率随偏心量的增大而增大,理论计算结果与模拟结果吻合,偏心量不大于0.2 mm时,误差不超过3%,但也呈现出随偏心量的增大,误差增大的趋势,该结论与 GRAVISS[27]所得结果一致。 为更全面地总结环形间隙密封的泄漏率计算方法,现对对周向线速度的影响也作大致说明。当存在周向相对转动时,间隙中流体在周向为剪切流,在轴向为压差流,用流量因子来判定流态,计算方法[28-29]如下: 式中 Rec,Rea—— 单独考虑周向剪切流动和轴向压差流动时的雷诺数。 规定ξ<9/16时表示流体处于层流状态,ξ>1时为湍流状态。本文中周向平均线速度近似取: 式中 v0——转子转动的线速度。 轴向平均线速度va采用式(3)计算,即va=vm,且 Δp=0.15 MPa,η=0.041 Pa·s,h=0.25 mm,l=140 mm。计算后可知,Rea非常小,可忽略不计,若要使流动处于湍流状态,则vc需达到600 m/s以上,所以在所分析的相对运动速度范围内,流动基本都处于层流状态,计算时采用层流模型。 WEISSENBERGER[19]和 YAMADA[20]认 为当环形间隙内流动为层流时,即便存在内外壁面相对运动,依然可采用式(1)计算泄漏率,但本文数值研究结果(见图8)却与之不同。图中计算结果显示:泄漏率随周向线速度的增大而显著减小,即便在速度较小时,该现象也较为显著,不过泄漏率的降低幅度随周向线速度的增大而逐渐减小,这一现象可能与流体的近壁面剪切特性密切相关,鉴于此,后续将作进一步深入研究。 图8 周向线速度对泄漏率的影响Fig.8 Influence of circumferential linear velocity on leakage rate (1)采用层流模型对环形间隙进行数值计算,结果与试验数据基本吻合。数值计算时,液膜厚度方向网格层数不小于4层,网格单元纵横比(Aspect Ratio)控制在1~1.5,可获得准确的泄漏率计算结果。 (2)表面粗糙度对处于层流状态下的泄漏率几乎无影响,而在紊流状态下,表面粗糙度越大,泄漏率越小,且泄漏率随着雷诺数的增加而增大,当雷诺数达到某一值后,泄漏率不再变化。 (3)文献[16]的理论公式乘以修正系数2后,可准确计算锥形间隙的泄漏率。采用文献[15]的理论方法,可准确计算存在偏心量时的环形间隙泄漏率。 (4)环形间隙密封泄漏率受旋转速度的影响显著,速度越大,泄漏越少,小转速时也体现出显著的泄漏率下降趋势,这与现有文献[19-20]的研究结论不一致。
3.3 偏心的影响
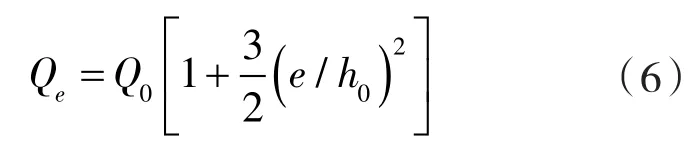

3.4 周向线速度的影响


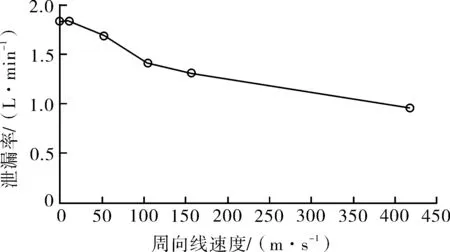
4 结论
