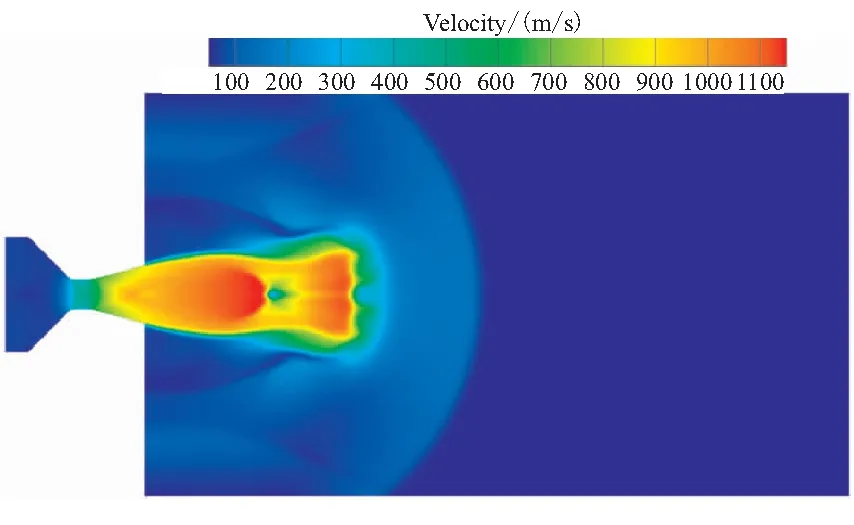
火箭弹自力弹射低压室流场特性数值分析*
2021-02-16宋向华佘湖清
宋 健,宋向华,蔡 蒨,佘湖清
(中国船舶第710研究所,宜昌 443000)
0 引言
舰载多管火箭弹发射装置执行作战任务时,火箭发动机工作产生的尾焰可能对甲板上的人员和设备造成危害。借鉴同心筒发射方式的火箭弹自力弹射技术方案,可在兼容现役舰载火箭弹的基础上,消除尾焰对发射装置后部空间的负面影响。
火箭弹自力弹射过程中弹体前进的动力包括发动机自推力Ft和弹射力F1。弹射力由发动机工作时产生的燃气在弹后空间建立压强产生,火箭发动机自身即为燃气发生装置,因此称为自力弹射。燃气注入弹体后部空间后,导致发射筒内压强升高,不过相对于发动机工作压强仍较低。因此,称弹体后部的筒内空间为低压室。相对于火箭弹自力发射,自力弹射的发射动力及尾流场结构等产生了显著变化。因此,开展自力弹射低压室燃气流场特性的数值研究具有重要的应用价值。
赵谢等[1]研究了导流锥锥型对燃气弹射内弹道的影响,发现锥型母线为曲线时改变了燃气反射点的位置,避免了燃气沿直线锥型直接冲向筒底导致的二次压力冲击,且曲面锥能够提高导弹的出筒速度,缩短出筒时间。张程等[2]提出了一种外方内圆的异型同心筒发射装置,通过对其发射过程的非定常数值模拟,证明异型同心筒可实现燃气的顺利排导,结合试验为该异型结构同心筒发射装置的研制提供了理论支撑。于勇等[3]针对同心筒发射时弹底部受到的附加弹射力及其影响因素展开研究,表明筒底所受冲击力与附加弹射力正相关,减小内外筒缝隙可提高弹底所受的附加弹射力;增加导流锥后将对燃气流动的震荡及冲击力产生影响。张英琦等[4-5]建立了同心筒发射内弹道数值计算模型,并开展了实弹发射试验,研究结果表明,内筒收缩段和适配器的增加使得内外筒间隙温度及其峰值显著增加,分析总结了同心筒内筒及外筒温度场的分布规律,研究了同心筒发射装置的热响应特性。程洪杰等[6]研究了初始容积对燃气弹射内弹道性能的影响,发现随初容室高度增加,对于弹底初始冲击压力峰值,容积因素占据主导,对于二次压力峰值,总压因素占据主导;导弹加速度峰值和出筒速度先减小后增加,出筒时间先变长后变短。郑榆淇等[7]为满足带折叠舵翼导弹的同心筒发射需求,设计了一种外圆内方的类同心筒发射装置,针对发射过程中的燃气流动特性进行了计算分析,发现燃气排导间隙减小会增强发射筒内的压强。张程等[8]研究了内筒收敛段的收敛角度以及筒口扩张段的扩张角度对同心筒发射流场的影响,研究结果表明,内筒收敛段的存在使得燃气排导更为通畅,筒内的热环境有所改善;筒口扩张段对改善导弹热环境也有明显影响。程洪杰等[9]研究了导流锥参数对弹射筒内压力冲击平滑效果的影响,结果表明,导流锥的结构直接决定燃气飞溅现象的产生和流场结构的紊乱程度,导流锥结构经过优化后可以较大程度地缓解压力冲击现象。胡晓磊等[10]针对同心筒热发射燃气射流二次燃烧冲击效应问题展开研究,发现随着导弹尾部离发射筒口越来越远,反溅激波逐渐减弱,筒口增加导流板能够降低导弹出筒时弹体表面的温度。
本文以某型火箭弹自力弹射装置的低压室燃气流场特性为研究对象,运用数值计算方法对火箭弹自力弹射的出筒过程进行了非定常数值模拟,以明确自力弹射过程中低压室燃气流场的特性,为自力弹射技术的后续研究及应用提供支撑。
1 数值模型
火箭弹自力弹射系统主要由发射筒、火箭弹等组成,如图1所示。

图1 自力弹射装置示意图
1.1 基本方程
进行自力弹射低压室燃气流场的非定常数值模拟时,采用燃气和空气双组分混合流动模型,两种组分均满足理想气体状态方程。因为火箭弹自力弹射装置具有轴对称的结构特点,所以采用非定常二维轴对称Navier-Stokes方程组对自力弹射低压室燃气流场进行数值模拟,控制方程如下:
(1)
式中U为守恒变量;F、G为对流项通量;Fvis、Gvis为扩散项通量;H为轴对称源项,表达式如下:
U=(ρρuρvE)T
F=(ρupu2+pρuv(E+p)u)T
G=(ρvρuvρv2+p(E+p)v)T
Fvis=(0τxxτxyuτxx+vτxy+qx)T
Gvis=(0τxyτyyuτxy+vτyy+qy)T
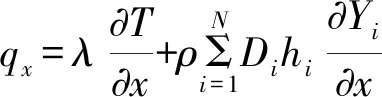
采用雷诺时均方法建立数值计算模型以求解上述控制方程。为封闭雷诺时均方程的雷诺应力项和输运项,由此引入湍动能k和湍流耗散率ε。由于自力弹射流场轴向部分为高速射流,临近筒底部气流速度近似滞止为零,故湍流模型采用既适合低雷诺数又适合高雷诺数的RNGk-ε湍流模型[11],该模型可有效用于射流和混合流的自由流动。
湍流动能方程为
Gk+Gb-ρε-YM
(2)
湍流动能耗散率方程为
(3)
式中αk、αε分别为湍动能和湍能耗散率的逆有效普朗特数;Gk为由于平均速度梯度引起的湍动能产生项;Gb为由于浮力引起的湍动能产生项;YM为可压缩湍流的脉动扩张给全部耗散率带来的影响。经验常数Cμ=0.084 5,C1ε=1.42,C2ε=1.68,μeff=μ+μt。
1.2 组分输运方程
在进行自力弹射低压室燃气流场仿真计算时,将燃气和空气均视为单一均匀气体,混合气体的属性由理想气体混合定律定义:
(5)
式中R为通用气体常数;Mw,j为第i种组分摩尔质量;cp,i为第i种组分比定压热容。
多组分输运方程为
(6)
式中Ri为第i种组分由化学反应带来的净生成率;Si为第i种组分由离散相及用户自定义的源项带来的净生成率。
组分扩散通量为
gJi=-ρDi,mYi
(7)
式中Di,m为混合介质中组分i的扩散系数。
1.3 弹体运动规律
火箭弹在自力弹射过程中,弹体所受合力为
F=F1+Ft-Ff-Fg-Fp 0
(8)
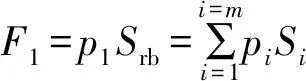
在弹体出筒过程中,通过UDF获取实时的流场参数,计算得到弹体受力,以此确定弹体在任一时刻的加速度及速度,并更新计算网格,仿真过程中,忽略弹体的径向运动。t时刻,火箭弹沿轴线的速度为Vt,弹体位移为lt,弹体重量为md,Δt为计算时间步长,则
弹体速度为
(9)
弹体位移为
lt=lt-Δt+Vt×Δt
(10)
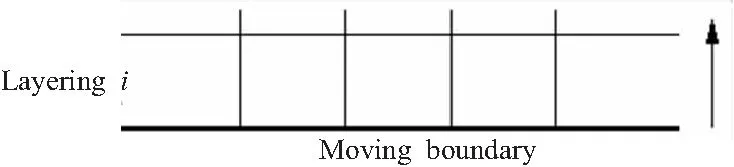
根据计算得到的弹体运动速度,使用分层动网格法对低压室燃气流场的计算网格进行更新,实现弹体出筒过程的非定常数值模拟。分层动网格的重构方式如下:初始时刻网格如图2所示,第j层网格与移动边界相邻,其高度h将根据移动边界的运动发生变化。
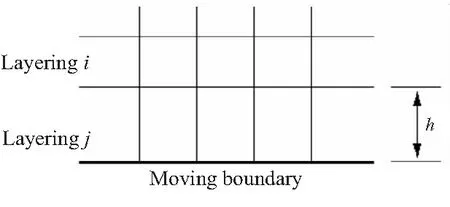
图2 初始网格模型
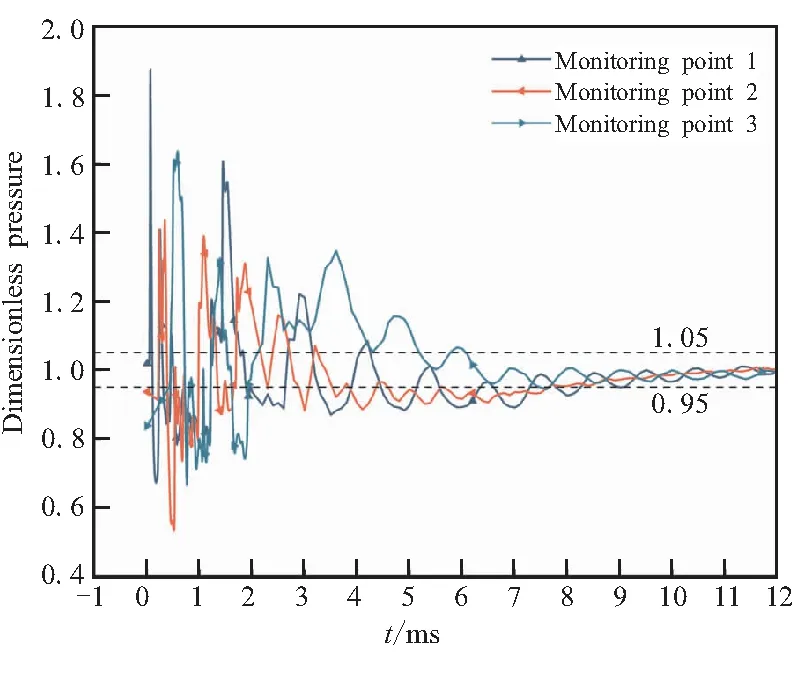
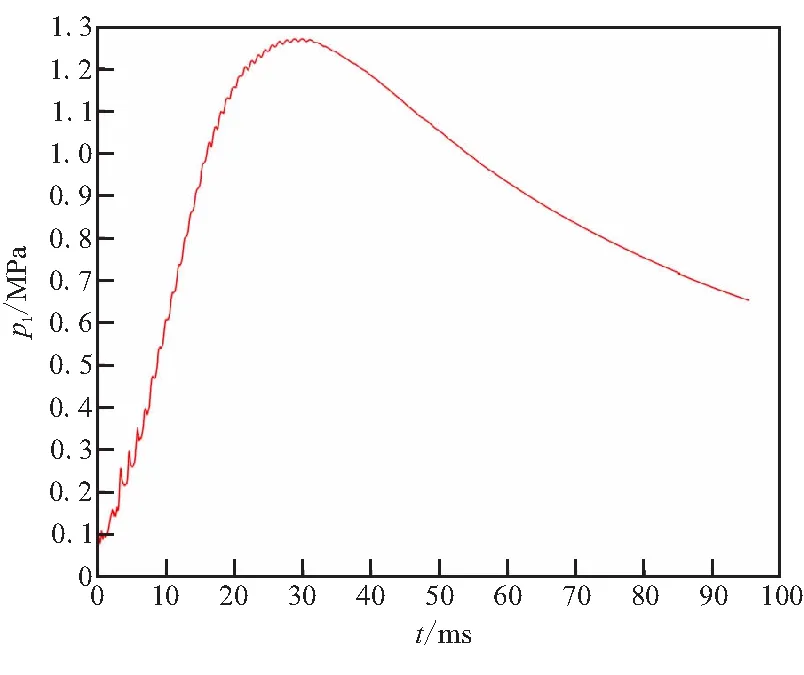
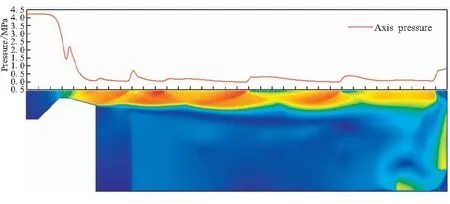
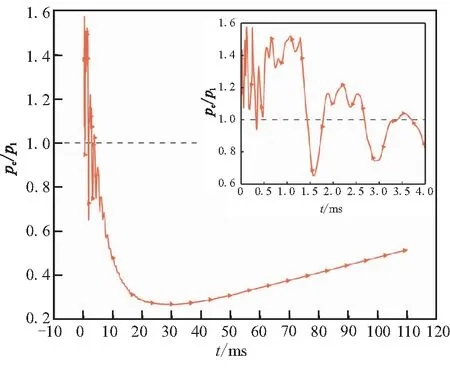
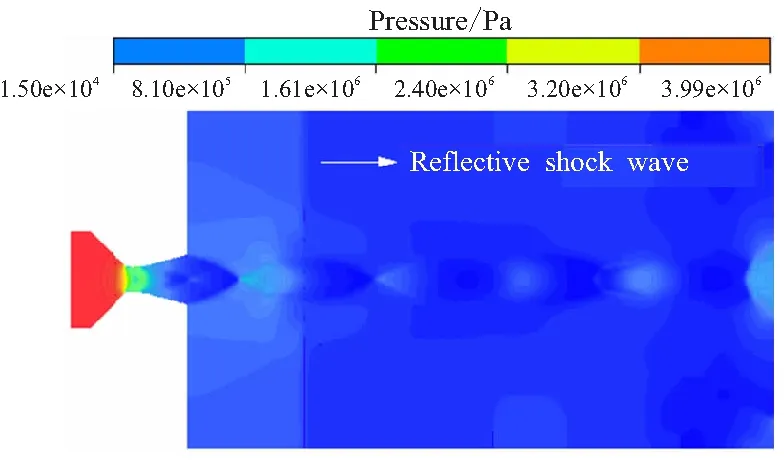
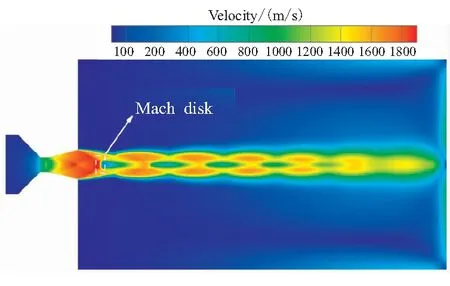
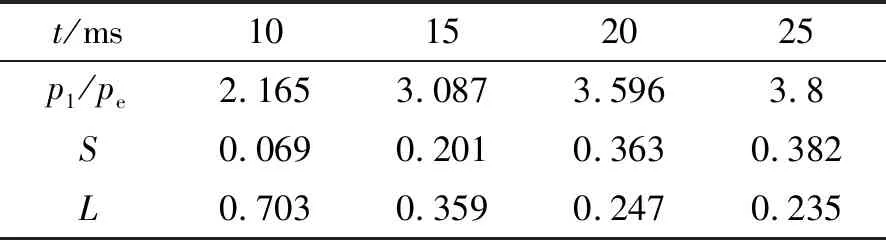
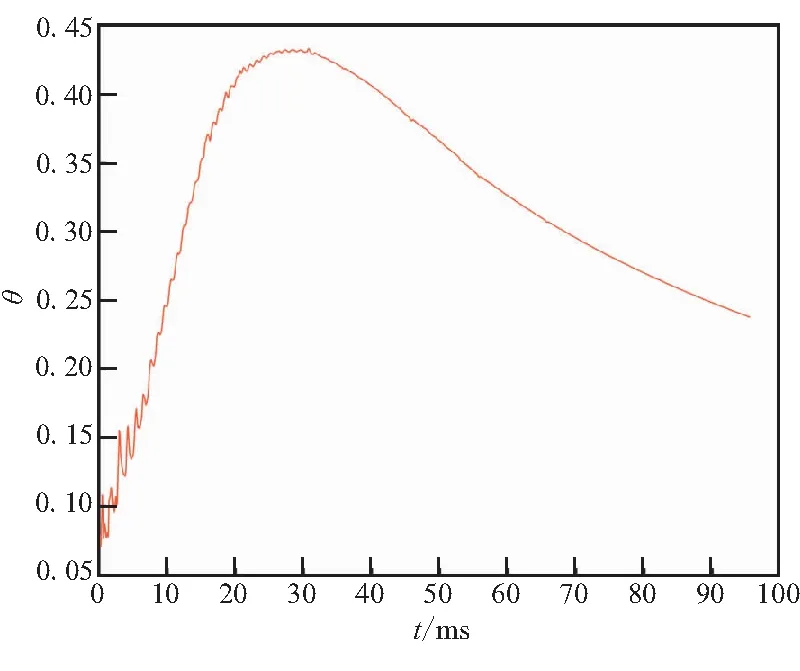
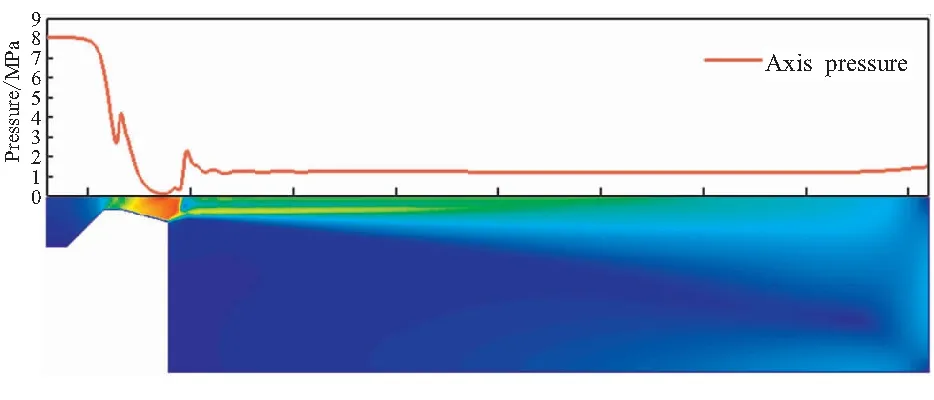
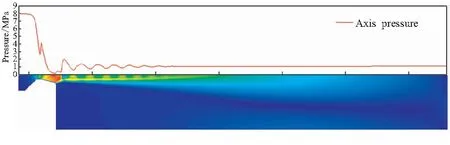
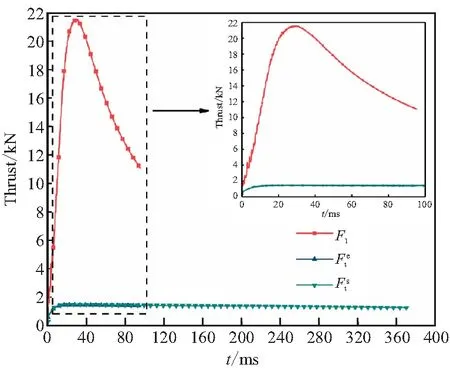
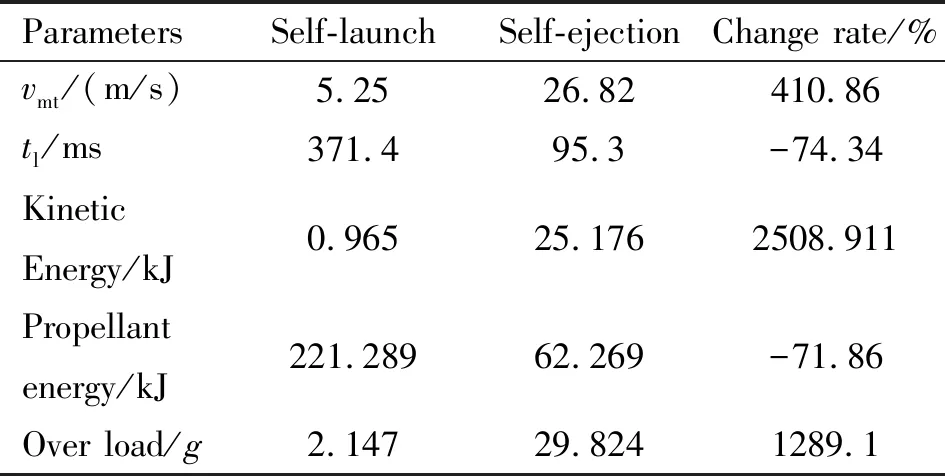
如果移动边界的运动导致第j层网格发生拉伸变化,当其高度h满足hmin>(1+αs)hideal时,j层网格分裂形成新的j层网格和k层网格如图3所示。其中,hmin为第j层网格高度的最小值,hideal为理想网格高度,αs为网格分裂因子。如果移动边界的运动使得第j层网格发生压缩,当其高度h满足hmin 图3 分裂后网格 图4 融合后网格 针对自力弹射装置的结构特点,采用轴对称计算模型对发射过程中低压室内的燃气流场进行数值模拟。流场计算网格全部采用结构化网格,并在喷管喉部处进行加密,自力弹射低压室燃气流场的初始计算网格及边界条件如图5所示。 图5 初始计算网格与边界条件 自力弹射低压室燃气流场数值模拟过程中,设定只有燃气和空气两种组分,燃气组分的部分参数如表1所示。 表1 燃气组分部分参数 求解器采用压力基求解器,采用有限体积法对控制方程进行离散,压力-速度耦合采用PISO算法。在数值模拟过程中,喷管入口AI为压力入口条件,HI为轴线条件,发射筒壁面及喷管壁面等部位采用无滑移壁面边界条件。发动机喷管以外计算区域的初始参数取静止大气参数:p=101 325 Pa,T=300 K;喷管压力入口的总压随时间变化如图6所示,总温为1878 K,气体组分为燃气组分。 燃气射流流场的数值计算精度对网格数目有较强的依赖性,因此需要开展自力弹射低压室燃气流场数值模拟的网格无关性验证。本文共建立了3种尺寸的网格模型:模型A为1.5万计算网格;模型B为2.5万计算网格;模型C为3.0万计算网格,三种网格模型在5 ms时刻轴线的压力数据如图7所示。可见,模型B和模型C的轴线压力数据的一致性较好,模型A与二者有一定差异。 图6 喷管入口总压曲线 图7 不同网格模型5 ms时的轴线压力 在图5中的观测点P0,将模型A和模型C在1 ms和5 ms时刻的温度值和压力值与模型B进行对比,结果如表2所示。 表2 不同网格模型的计算数据对比 由表2可知,模型A与模型B在P0点温度和压力的最大误差6.16%;模型C与模型B在P0点温度和压力的最大误差为1.45%。综合考虑计算过程中流场网格数量的增加及数值计算效率和计算精度等因素,选用模型B进行火箭弹自力弹射低压室燃气流场的仿真分析。 火箭弹自力弹射低压室内的燃气流场类似于超声速冲击射流流场,其核心部分均为射流冲击固定壁面。因此,采用本文的数值模型对文献[13]的超声速冲击射流案例进行仿真。图8为验证案例的计算网格及边界条件,表示通过射流中心轴线的一半计算区域。喷管总压与环境压强比值p0/pa=2.5,h/d=2(h为喷管出口距平板距离,d=25.4 mm为喷管出口的直径),仿真与试验的数据对比如图9和图10所示。由图9可见,采用本文数值模型仿真得到的流场结构与试验纹影图吻合良好;由图10可知,数值仿真得到冲击平面上的压强系数[Cp=(p-pa)/(p0-pa)]与试验数据的一致性较好,表明本文建立的数值模型可用于自力弹射低压室燃气流场的数值模拟。 图8 计算网格及边界条件 (a)Experiment schlieren (b)Density contour 图10 仿真和试验的冲击平面压强系数 火箭弹发动机开始工作后,发动机内压强较大,低压室内压强仍为大气压,燃气射流为非定常欠膨胀射流,射流由喷口向外发展的同时,燃气与空气之间形成的一道高压界面也被射流向下游推进。发动机作为扰动源不断向低压室内传播压缩波,由于后形成的压缩波传播速度更快,因此高压界面被不断压缩而形成起始冲击波,射流的方向性决定了起始冲击波的方向性,如图11所示[14]。起始冲击波离开喷管后不再受到喷管壁面的限制作用,迅速膨胀成为球形冲击波。由于射流从喷管出口截面喷出后对低压室内空气的卷吸效应,在喷管出口附近区域形成低压涡。 图11 0.15 ms时刻的速度云图 在起始冲击波与低压室侧壁发生碰撞之前,冲击波不受空间约束而自由膨胀,直至与低压室侧壁发生碰撞,该阶段火箭弹自力弹射与自力发射的燃气射流流场特性相同。 起始冲击波与低压室侧壁发生碰撞后,形成弓形反射激波。由于低压室壁面与起始冲击波运动方向近似垂直,碰撞后形成的弓形反射激波与起始冲击波相互碰撞叠加,在低压室侧壁面形成局部的高压区,如图12所示。 图12 0.265 ms低压室侧壁压力和速度云图 起始冲击波在低压室内继续向筒底转播,其前沿呈弧形分布,低压室底部中心区域最先受到冲击波的撞击,撞击发生后压强迅速上升。由数值模拟数据可知,在0.657 ms时,冲击波首次到达低压室底部,此时底部中线的压强分布如图13所示。 图13 0.657 ms时刻的筒底压力分布 低压室内起始冲击波撞击到筒底部后,将发生反射,根据激波前后的参数关系式Rankine-Hugoniot方程[15],得反射激波前后的压强关系式: (11) 式中ps1为入射激波运动方向前方的压强值;ps2为入射激波后方的压强值;ps3为反射激波运动方向前方的压强值;k为气体比热比。 起始冲击波以声速向低压室底部传播,燃气流经喷管扩张段加速后,才可达到超声速流动。因此,燃气的传播速度在流场起始阶段滞后于起始冲击波。当起始冲击波与低压室底部发生碰撞时,燃气仍未到达底部,如图14所示。此时,低压室底部仍为空气。因此,式(11)中的比热比k取值为1.4。 图14 0.657 ms时刻的密度云图(上)和组分云图(下) 由0.657 ms的压强云图,得到ps1=101 600 Pa,ps2=112 669 Pa,将二者代入反射激波前后压强关系式中计算,得到ps3=124 756 Pa。通过燃气流场仿真得到ps3=124 349 Pa,流场仿真结果与式(11)的计算结果基本保持一致。 起始冲击波在筒底发生碰撞后形成的反射激波向弹体底部传播,且由式(11)可知,其强度有所增加。由于反射激波的传播方向和燃气射流的运动方向相反,因此射流核心区域对反射激波有较强的阻滞作用,在低压室底部中心区域附近形成一个高压区,如图15所示。由于此时的燃气射流核心已形成超声速流动,因此反射激波不会影响射流核心区域的燃气流动状态,而是“绕过”射流核心向弹底部传播。 图15 0.975 ms时刻的轴线压强和速度云图 表3 监测点坐标 图16 各监测点的 燃气射流结构形成后,喷管不再向外传播压缩波,冲击波逐渐衰减,同时随着燃气注入低压室,低压室内平均压强不断升高,激波两侧的压差减小,其强度随之降低,低压室内的流场分布逐渐趋于均匀。当压强震荡幅度小于5%时,可认为由起始冲击波及反射激波引起的震荡消失,流场分布趋于均匀。 火箭弹自力弹射出筒过程中,燃气一直被限制在弹体后部的低压室内,流场初始阶段随着发动机工作生成的燃气不断注入低压室,低压室压强p1不断升高;随后弹体运动速度快速增加,燃气的注入不能弥补低压室体积增加带来的压强损失,p1开始下降,p1随时间的变化如图17所示,低压室压强的变化直接影响低压室内的流场结构。 图17 低压室压强随时间变化曲线 发动机开始工作初期低压室内压强仍为大气压强,通过喷管流出的燃气压强大于低压室内压强,燃气流处于欠膨胀状态。0.3 ms时刻喷管出口压强pe和背压p1的比值pe/p1=1.196,为中度欠膨胀状态,此时低压室内的速度云图如图18所示。 图18 0.3 ms的速度云图 起始波节内射流核心遇到由喷管唇部传来的膨胀波经历了膨胀过程,之后遇到穿过轴线从喷管唇部相反方向传来的膨胀波后进一步膨胀。经过交叉膨胀波后,燃气射流压强值低于背压,因此背压会使得射流边界向内收缩。膨胀波在射流边界反射后产生的压缩波将避免燃气发生过膨胀,以满足射流边界上的等压条件。经过压缩波后,燃气射流压强再次超过背压达到欠膨胀状态,继续向低压室底部传播[16]。 由于0.657 ms时刻起始冲击波已经撞击到低压室底部并产生反射,底部中心区域的压强升高。当射流遇到低压室底部中心的高压区后,射流结构受到影响发生径向偏移,如图19所示。 图19 1.5 ms的轴线压强及速度云图 火箭弹自力弹射过程中发动机工作的背压较高,是其与自力发射的最大差别之一。从图20中可见,在低压室燃气流场的初始阶段,燃气流会在欠膨胀状态和过膨胀状态之间反复转换。经分析,这种转换是由于初始冲击波及反射激波在低压室内引起的流场震荡所导致,后续随流场震荡的消失,燃气流稳定在过膨胀状态,直至弹体出筒。在0.35 ms时刻附近燃气流由欠膨胀状态转变为过膨胀状态,此时的流场结构见图21。起始冲击波与低压室侧壁碰撞形成的弓形反射激波运动至喷管出口附近,导致喷管出口的燃气流压强小于背压,形成过膨胀燃气流。 图20 喷口压强与背压的比值曲线 图21 0.35 ms时刻的压力云图 随发动机内的压强升高,喷管出口燃气的压强也相应升高,燃气流重新转变为欠膨胀状态,但在1.59 ms时刻附近燃气流再次转变为过膨胀状态,此时流场结构如图22所示。由起始冲击波在筒底部反射形成的反射冲击波到达弹体底部并继续发生反射,导致喷管出口燃气流压强小于背压,形成过膨胀燃气流。 图22 1.59 ms时刻的压力云图 3.5 ms时刻附近的欠膨胀状态同样是由于自力弹射低压室燃气流场起始阶段的震荡所导致。随低压室流场震荡的消失,3.7 ms后,喷管出口燃气流开始稳定在过膨胀状态。从图17可见,随弹体向前运动,低压室体积快速增加,背压会逐渐停止增长并下降,pe/p1的值有所上升,但仍小于1,在弹体出筒前,喷管出口燃气流始终处于过膨胀状态。 过膨胀状态的燃气射流进入低压室后,通过一系列斜激波向轴线偏转,同时压强升高。由于射流核心的燃气流在经过喷管出口截面后继续膨胀,与背压的压差增大,斜激波不能提供所需的压缩能力。因此,在射流轴线会形成马赫盘结构,如图23所示。 喷管出口的过膨胀射流经过激波后被过度压缩,压力高于背压。为与背压达到平衡,射流通过一系列膨胀波向外偏转同时压力减小,该部分膨胀波是第一个波节内斜激波从射流边界反射而来。之后,射流再次遇到由轴线反射而来的膨胀波而发生过膨胀,压力再次低于背压。膨胀波碰到射流边界后向轴线反射产生压缩波,这些压缩波使得射流向轴线偏转,且压力升高,如果压缩波的强度足够高,将再次产生斜激波并形成马赫盘。这个过程不断重复,从而形成多个马赫盘。由于气体存在粘性,在射流边界处空气和射流之间产生了湍流剪切层。湍流剪切层会产生粘性阻力将激波的能量转化成热量耗散掉,且射流每次经过激波后总压都会有损失,最终射流和环境之间的压差消失,不能继续产生激波,后续燃气和空气的混合区不断向轴线扩散,最终导致射流核心完全消失[16]。 图23 10 ms时刻的速度云图 随着背压的进一步升高,燃气射流的流场结构也会相应发生变化,马赫盘面积SMa不断增加,同时马赫盘向射流上游移动,距喷管出口的距离LMa不断减小。以喷管出口面积Se和喷管出口直径De对马赫盘面积SMa和马赫盘距喷口距离LMa进行无量纲化处理:S=SMa/Se,L=LMa/De。不同时刻的S和L数据见表4。 表4 不同时刻的S和L 数据 由表4数据可知,随背压与喷管出口压力比值的增大,马赫盘面积逐渐增大,距离喷口的距离不断缩小。根据气体动力学的相关知识,当背压超过喷管的第二临界反压值时,马赫盘将会进入喷管,导致喷管出口截面不能获得超声速流,第二临界反压值可通过下式求得: (12) 式中pc为喷管入口总压;p1为低压室内压强;k为燃气的绝热指数;Mae为喷管出口的马赫数。 θ最大值为0.433,即背压始终未超过喷管的第二临界压强,因此马赫盘不会进入到喷管内,喷管内部的流动不受低压室压强变化的影响。 由图24可知,喷管背压最大的时刻为28.3 ms,此时S达到最大值0.442;L达到最小值0.201,此时的流场结构及轴线压强如图25所示。正激波仍在喷管下游,没有进入喷管。反压的升高使得正激波强度增大,燃气流经过激波后总压损失较大,不能继续形成激波结构。在低压室底部,由于燃气流速近似滞止为零,形成了局部的高压区。 图24 θ随时间变化曲线 图25 28.3 ms时刻的轴线压强及速度云图 在28.3 ms之后,由于背压p1开始减小,同时θ值也开始减小,但结合图20可知,在弹体出筒前,喷口压强pe始终小于背压p1,燃气射流始终处于过膨胀状态。50/100 ms时刻的轴线压强及速度云图如图26所示,可看到50/100 ms时刻的流场结构为典型的过膨胀燃气射流结构,燃气流出喷管后形成一系列激波,燃气向筒底部传播的过程中,轴线压强不断降低,激波强度逐渐减弱,最终消失。 (a)Axis pressure and velocity contour at 50 ms (b)Axis pressure and velocity contour at 100 ms(local) 通过数值仿真得到的自力发射推力时间曲线和自力弹射推力时间曲线如图27所示,对曲线积分得到在弹体出筒前各推力的总冲量,如表5所示。由图27和表5可知,弹射力F1是火箭弹自力弹射过程中的主要动力。 图27 推力对比图 表5 不同推力的总冲量 在相同弹体参数及发射筒长度的条件下,火箭弹自力发射和自力弹射的速度时间曲线vm-t如图28所示。从图28中可看出,自力弹射的出筒速度要远大于采用相同发动机的自力发射,出筒时间也更短。因此,在相同离筒初速的条件下,自力弹射所需的推进剂量更少,能量利用率更高。 由于发动机工作产生的尾焰一直被限制在自力弹射装置的低压室内,通过膨胀做功进一步将燃气内能转换为弹体动能,为弹体提供额外的前进动力。相比于自力发射,自力弹射极大的提高了装药的能量利用率,可用更少的装药获得相同的出筒速度。但同时发射装置也将承受较大的后坐力,弹体离筒过程中的过载也较大。结合某特定型号火箭弹发动机参数及弹体参数,在相同发射条件下,自力弹射和自力发射的内弹道参数对照如表6所示。表6中,变化率(Change rate)为自力弹射相对于自力发射的变化率;vmt为弹体出筒瞬间速度;t1为弹体在筒内运动时间;g为当地重力加速度,取9.8 m/s2;弹体自重70 kg。 图28 自力弹射和自力发射的弹体速度时间曲线 表6 自力发射和自弹发射内弹道参数对比 (1)自力弹射过程的初始阶段会产生起始冲击波,撞击到低压室底部后发生反射,反射激波的数值模拟数据与公式计算数据保持一致;起始冲击波与反射激波导致低压室燃气流场初始阶段的震荡,随低压室内的平均压强不断升高,激波强度减弱,流场震荡结束。 (2)自力弹射过程中随着弹体向前运动,喷口燃气流会在欠膨胀状态与过膨胀状态之间反复转换;随后流场震荡消失,燃气流始终处于过膨胀状态,直至弹体出筒。 (3)通过数值模拟得到某特定型号火箭弹在相同发射条件下自力弹射和自力发射的内弹道数据,相比于火箭弹自力发射,自力弹射的出筒速度提高410.86%,出筒时间缩短74.34%。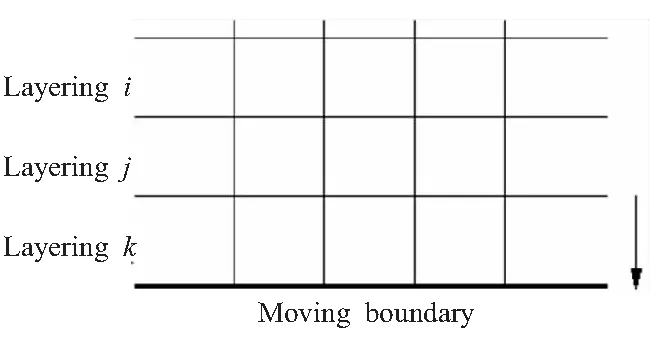
2 计算模型与条件
2.1 计算区域
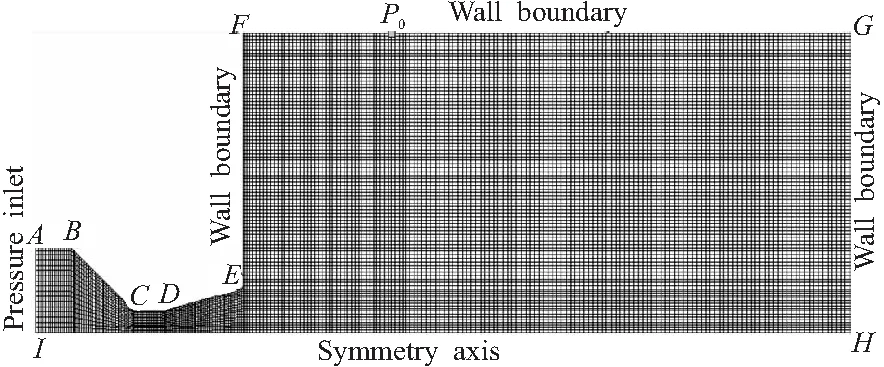
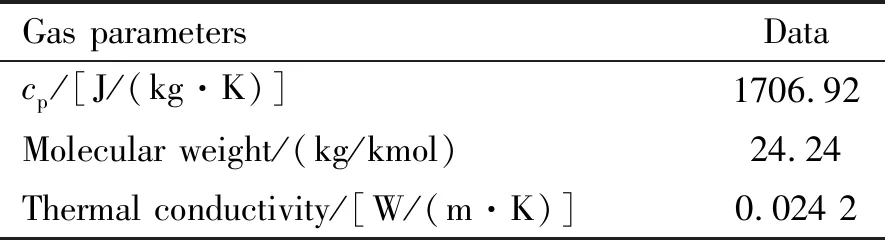
2.2 条件设置
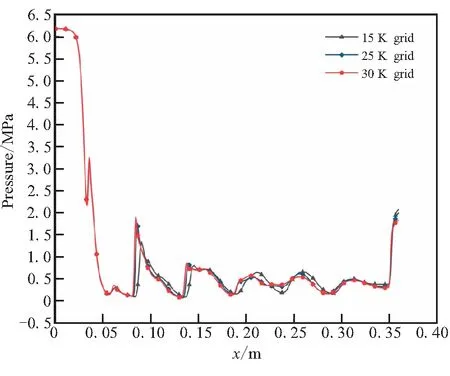
2.3 网格无关性验证


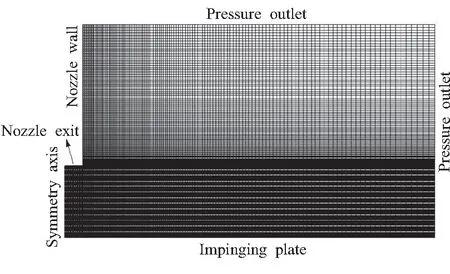
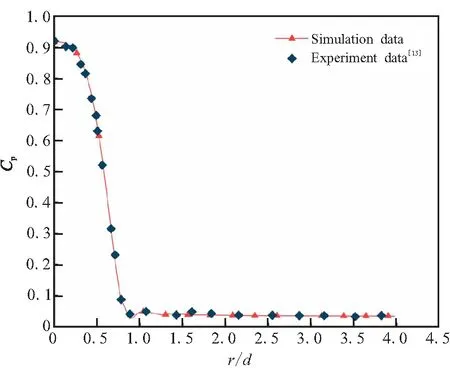
2.4 数值模型验证

3 数据分析及讨论
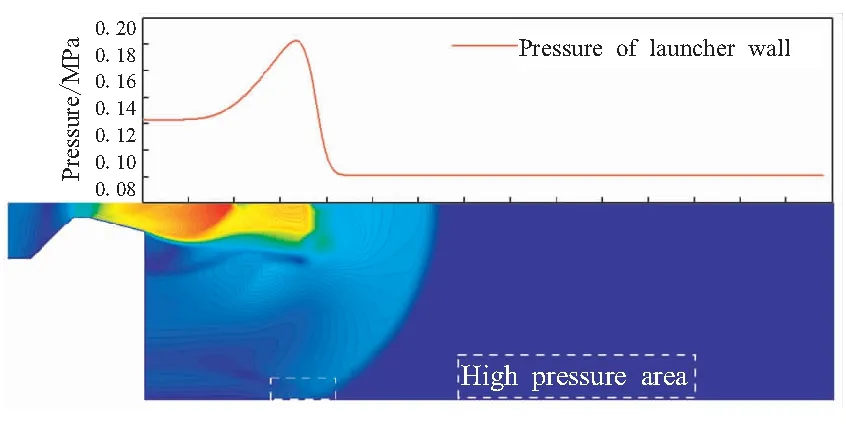
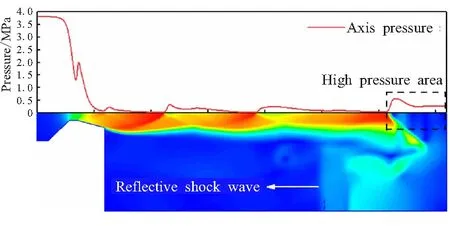
3.1 自力弹射低压室流场的初始冲击波



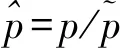

3.2 弹体运动对低压室流场结构的影响

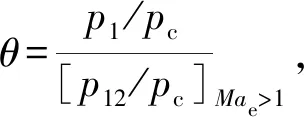
3.3 自力弹射内弹道特性
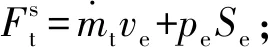



4 结论
