具协作狩猎和恐惧效应的扩散捕食者-食饵系统分析
2021-02-15刘宇鑫张继民
刘宇鑫, 张继民
(黑龙江大学 数学科学学院, 哈尔滨 150080)
0 引 言
捕食关系是自然系统中最基本的关系之一, 在种群进化、保护生物多样性方面发挥着重要作用[1-2]。很多捕食者都是群居生活, 在捕食过程中,为了捕获猎物, 它们之间需要相互协作狩猎, 这样极大地提高了捕食者的生存率。捕食者不仅可以直接捕杀食饵, 也可以对食饵产生间接影响, 形成一种捕食者恐惧效应, 导致食饵栖息地的变更、觅食习惯的改变和生殖率下降等。
在文献[3]中, 学者Alves等首先建立了一个具协作狩猎的捕食者-食饵系统, 通过数值模拟研究了系统平衡点的存在性及稳定性、分支的存在性。Pal等讨论了一个离散的具协作狩猎的捕食者-食饵系统的动力学性质, 数值模拟显示协作狩猎可以引起混沌行为[4]。Banerjee等考虑了一个三种群捕食系统, 捕食者协作狩猎两个互惠的食饵[5]。Song等考虑了具协作狩猎的扩散捕食者-食饵系统, 并证明系统具有图灵结构[6]。在文献[7]中, Wang等首先提出了一个两维具食饵恐惧效应的捕食者-食饵系统, 指出恐惧效应能够稳定捕食者-食饵系统。在此之后, 许多具有不同背景的具食饵恐惧效应的捕食者-食饵系统被研究和分析[8-10]。
基于上面的分析和讨论, 本文主要研究一类具协作狩猎和恐惧效应的扩散捕食者-食饵系统
(1)
式中:u表示食饵种群密度;v表示捕食者种群密度;Ω是n中一个有界区域且具有光滑的边界;r0是食饵出生率;d是食饵死亡率;a是食饵种内竞争系数;p是捕食者捕食率;α是协作狩猎参数;m是捕食者死亡率;e是恐惧效应参数;c是营养转化率;d1,d2分别表示食饵种群和捕食者种群的扩散系数。本文中假设所有的模型系数都是正的。
本文主要目的是分析系统(1)的动力学性质。第1节是系统的基础动力学性质, 包括解的全局存在性和耗散性。第2节探讨系统常值稳态解的存在性和局部稳定性, 并给出Hopf分支的存在性。第3节利用数值模拟验证所得结果。
1 解的全局存在性和耗散性
研究系统(1)解的长时间性质, 包括全局存在性和耗散性。

定理2若(u(x,t),v(x,t))是(1)的任意一个非负解, 则
(2)

证明设(u(x,t),v(x,t))是系统(1)的任意一个非负解, 则
由抛物方程的比较定理可知,式(2)的第一个不等式成立。
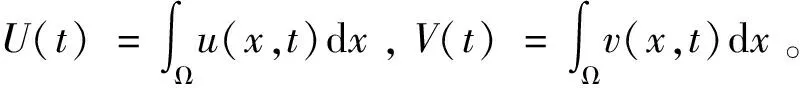
因而有

2 常值稳态解和Hopf分支
系统(1)的常值稳态解的存在性和稳定性及Hopf分支存在性。系统(1)的常值稳态解有

(3)
为了获得常值稳态解的稳定性, 令
μi∈Λ:={μi:0=μ0<μ1<…<μi<…,i∈0}
(4)
是具齐次Neumann边界条件算子-Δ在Ω上的特征值, 其中0:=∪{0}。定义


(5)
式中(φ,φ)∈X, 并且

四季柚嫩梢长到20 cm要摘心,一般采用疏剪丛生瘦弱新枝梢或交叉的1-2年生枝梢,不宜重修剪;对树冠郁蔽、内膛通风透光差的单株,则适量“开天窗”疏大枝(多年生的),改善树冠内膛通风透光性能。重剪衰老树和树势弱树,促发新梢或更新树冠。采用短剪,刺激生长势较弱的枝梢抽生强壮的新梢。
λ2-Tiλ+Di=0,i∈0
式中
定理3E0总是存在的, 且若d>r0, 则E0是局部渐近稳定的。
证明由式(4)和式(5)可知,系统(1)在E0处对应的线性化系统k阶特征方程为
λ2-(-(d1+d2)μk+r0-d-m)λ+(d1d2μk+(d1m-(r0-d))μk-(r0-d)m)=0
若d>r0, 则对任意的k∈0, 特征值实部均为负的, 因而E0是局部渐近稳定的。
定理4(i)若d
证明由E1表达式知(i)成立。根据式(4)和式(5)可知,系统(1)在E1处线性化系统对应的特征方程为
(λ+d2μk+(r0-d))(λ+d1μk+m-cp(r0-d)/a)=0
若m>cp(r0-d)/a, 则对任意的k∈0, 特征值实部均为负的, 因而(ii)成立。
定理5(i)若m (ii)若 (6) 则E2是局部渐近稳定的。 ceα3v4+(cα2+2cepα2)v3+(2cpα+cep2α)v2+A1v+A0=0 (7) 式中 A1=cp2+cdepα+aemα+cα(d-r0),A0=am+cp(d-r0) 根据笛卡尔符号规则, 若A0<0, 则式(7)存在唯一的正根, 于是E2存在且唯一。 由式(4)和式(5)知,系统(1)在E2处线性化系统对应的特征方程为 λ2-Tkλ+Dk=0,k∈0 (8) 式中 (9) 因而, 若式(6)成立, 则E2是局部渐近稳定的。 证明由式(9)可得 因而定理结论成立。 利用Matlab进行数值模拟, 验证前面所得的相关理论结果。 (1)图1显示捕食者和食饵都灭绝。这里r0=0.4,m=0.02,a=0.01,e=1,α=0.01,p=0.1,d=0.401。因为r0=0.4<0.401=d,所以定理3的条件成立,E0是渐近稳定的。 图1 常值稳态解E0 (2)图2说明捕食者灭绝, 食饵存在且达到最大环境容纳量, 其中r0=0.4,m=0.1,a=0.08,e=1,α=0.01,p=0.4,d=0.35, 注意到m=0.08>0.07=cp(r0-d)/a, 定理4的条件成立, 因而E1是渐近稳定的。 图2 常值稳态解E1 图3 正常值稳态解E2 (4)图4说明捕食者和食饵共存于一个空间齐次周期解, 其中r0=0.4,m=0.3,a=0.01,e=1,α=0.1,p=0.4,d=0.1, 这意味着发生了Hopf分支, 定理6是正确的。

3 数值模拟




