三相Vienna整流器改进载波脉宽调制策略*

陈 岚 肖蕙蕙 郭 强 向文凯

三相Vienna整流器改进载波脉宽调制策略*

陈 岚1, 2肖蕙蕙1, 2郭 强1, 2向文凯1, 2

(1. 重庆理工大学电气与电子工程学院 重庆 400054；2. 重庆市能源互联网工程技术研究中心 重庆 400054)

考虑到滤波电感、开关器件寄生参数和控制延迟等影响因素，整流器可能工作于非单位功率因数状态。此时，整流器若采用传统基于载波的脉宽调制(Carrier-based pulse width modulation, CB-PWM)策略，则会产生电压电流极性不一致的区域，进而导致开关管误动作、降低整流器性能。为此，基于传统CB-PWM策略提出一种改进载波脉宽调制策略(Modified carrier-based pulse width modulation, MCB-PWM)来改善整流器过零点畸变现象。首先，基于三相Vienna整流器工作原理，建立两相旋转(-)坐标系下的数学模型；其次，详细分析传统CB-PWM策略引起网侧电流过零点处波形畸变的原因，设计补偿措施，给出所提MCB-PWM策略的具体原理；此外，结合传统双闭环控制，形成系统整体控制框图；最后，利用Matlab/Simulink仿真，将传统CB-PWM策略与所提MCB-PWM策略进行对比，结果表明，所提MCB-PWM策略能显著改善输入电流过零点畸变现象，理论分析的正确性和有效性得到了验证。

Vienna整流器；过零点畸变；CB-PWM；Simulink仿真

1 引言

电能质量要求日益升高，其中作为重要指标之一的谐波含量标准也相应提升。目前，抑制谐波主要是通过采用高功率因数的整流器来实现。三电平PWM整流器作为整流器发展的核心方向，相比传统两电平PWM整流器，交流侧电压电平数增多，网侧电流谐波含量低[1-3]。三相Vienna整流器因其具有较低的输入电流畸变率、开关器件电压应力小、可靠性高、效率高等优点而倍受重视[4-6]。

Vienna整流器的谐波性能与其调制策略息息相关[7]。为此，一些学者对其进行了相应研究[8-11]，文献[8-9]重点分析了Vienna整流器的空间矢量脉宽调制(Space vector pulse width modulation, SVPWM)技术，提出三电平向两电平等效转换的方法，虽直观、易于数字实现，但其与基于载波的脉宽调制(Carrier-based pulse width modulation, CB-PWM)相比，过程繁琐、计算复杂；文献[10]提出利用补偿电压分量注入法来实现对中点电位平衡的控制；文献[11]通过叠加零序分量实现正弦脉宽调制(Sinusoidal pulse width moolulation, SPWM)和空间矢量SVPWM调制的等效，降低了一定的计算复 杂度。

上述有关Vienna整流器调制策略的研究主要分为正弦脉宽调制(SPWM)、基于载波的脉宽调制(CB-PWM)和空间矢量脉宽调制(SVPWM)三类，这些调制策略在实现时理论上均须满足Vienna整流器稳定运行的重要前提条件，即整流器各相交流侧电压极性必须与对应相输入电流极性一致[12-13]。然而，现有文献大多忽略交流侧电感上的压降，近似认为整流器输入电压与交流侧电压相同后，再衡量重要前提条件。但在实际电路中，有时滤波器的压降较大不能忽略且硬件电路的实际控制信号存在延迟，这些影响因素都将导致电流在过零点处违背电压电流极性一致的前提，使输入电流产生畸变，引起谐波含量增高，整流器性能降低。

目前，国内外已有相关文献对变换器的过零点畸变问题进行研究[14-20]。文献[14]基于SPWM提出一种占空比前馈干预的方法，解决了三相四线制Vienna整流器输入电流在过零点处的畸变问题；文献[15]基于SVPWM策略，提出通过优化输入电流过零点附近扇区内冗余矢量的分配来避免Vienna整流器输入电流的过零点畸变；文献[16]针对带LCL滤波器的Vienna整流器，提出注入三个偏置电压的三层不连续PWM方法，消除不同功率因数和低通滤波器引起的电流过零失真；文献[17]提出一种在电网电压过零点前，交换单相逆变器低频支路控制信号的电流过零点畸变消除方案；文献[18]针对单相H桥逆变器，提出一种混合BCM策略，通过在电压过零区域重新排列驱动信号，将电感电流的三角波形修整为四边形，减轻了过零失真；文献[19]提出一种新的混合峰值电流控制策略，有效抑制了微型光伏并网逆变器输出电流的过零点畸变；文 献[20]针对非隔离型H6桥单相光伏逆变器，提出一种具有无功补偿功能的分段调制策略来改善电流过零点畸变；文献[21]提出一种占空比前馈补偿的数字控制，改善了有源功率因数校正系统电流的过零点畸变。上述研究多集中于逆变器的电流过零处失真，少量Vienna整流器的文献也仅专注于SPWM与SVPWM方面，有关CB-PWM的研究极少且不系统。

为此，本文针对三相Vienna整流器，提出一种基于载波实现的改进脉宽调制策略(Modified carrier-based pulse width modulation, MCB-PWM)来改善过零点畸变。首先，通过Vienna整流器工作原理的分析，建立-坐标系下的数学模型；其次，详细分析电流过零点畸变的原因，并提出MCB-PWM策略加以改善；再者，基于-轴数学模型采用传统双闭环PI控制，形成一整套控制策略；最后，通过传统CB-PWM与MCB-PWM的仿真比较，验证了所提调制策略的正确性和有效性。

2 Vienna整流器工作原理及数学模型

三相三电平Vienna整流器拓扑结构如图1所示。其中a、b、c分别为A、B、C相电网电压；a、b、c为对应相输入电流；为滤波电感和线路的等效电阻；为滤波电感；j1、j2(=a, b, c)为三相电路上下IGBT开关管，上下管状态互补；1、2分别为直流侧上下滤波电容，1=2=；load为阻性负载。

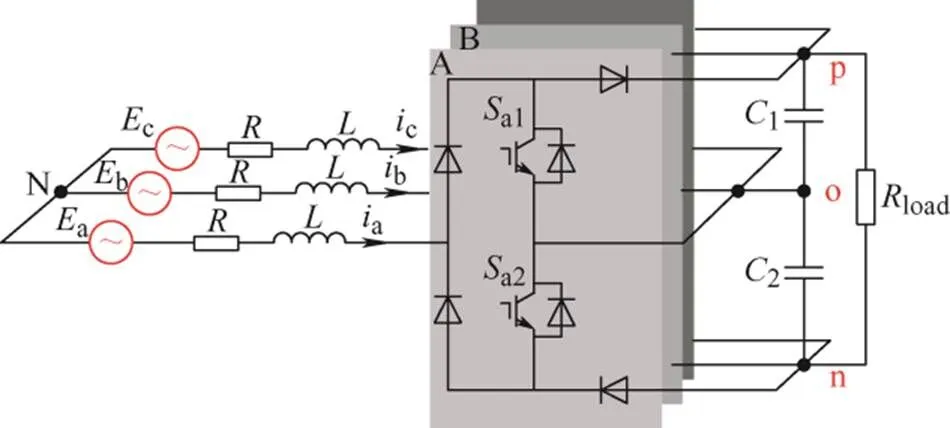
图1 三相Vienna整流器拓扑结构

由图1可见，A、B、C三相具有相同的电路结构，故以A相为例分析整流器的单相工作模态。此时设置分析前提：①三相输入电压平衡且无畸变；②整流器以单位功率因数状态工作；③电感电流处于连续导电模式(Continuous conduction mode, CCM)的电路模态；④开关频率远大于基波频率；⑤直流侧上下电容均压；⑥不计开关管的高频谐波分量。根据输入电压极性，A相电路状态可分为两类：a>0和a<0，电流走向相反。下面仅分析a>0的情况，如图2所示。根据开关管j1、j2开关状态，又可将其细分为两种模态，如图2a、2b所示，其状态分别如下：①a>0，j1导通、j2关断，桥臂电压Ao=O(0电平)；②a>0，j1关断、j2导通，桥臂电压Ao=P(dc/2电平)。

图2 Vienna单相工作原理分析图(Ea>0)

在三相输入电压平衡系统中，有

经上述电路原理分析，易得其旋转坐标系下数学模型为

式中，d、q为a、b、c的轴坐标分量；d、q为a、b、c的轴坐标分量；d、q为开关函数a、b、c的轴坐标分量。

由式(2)可见，坐标系下的系统非线性、强耦合，故本文整体设计里的双闭环即基于式(2)，从尽量消除耦合影响角度出发的。

3 调制策略分析

3.1 传统CB-PWM策略

忽略网侧电压在滤波电感上的压降，可得Vienna整流器基于载波脉宽调制方法中的三相参考电压aref、bref、cref可表示为

式中，m为三相参考电压的幅值，为三相电网电压的频率。

传统SPWM方法直接将三相正弦参考电压信号与三角载波进行比较生成PWM波，但调制基波电压的幅值最高也仅达直流电压的83.6%，故本文为提高直流电压的利用率且不影响输出电流的谐波特性，采用常用的3次谐波注入法加以改善，理论上能将电压利用率提高到99%左右。

三相Vienna系统的三次谐波offset表达式为

其中ref, max，ref, min表达式如下

三次谐波注入后的调制波aref, offset、bref, offset、cref, offset如式(6)所示

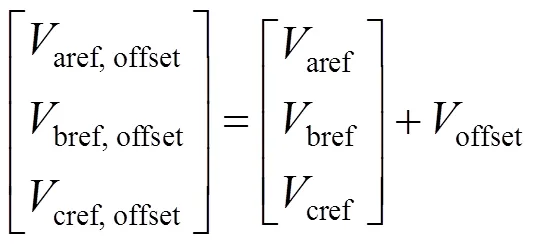
调制波与三角载波比较的波形如图3所示，此时调制波呈现马鞍波。

3.2 MCB-PWM调制策略

要保证Vienna整流器的正常运行，输入电压与电流极性相同是必要前提。然而，由于整流器电感、电阻和二极管性能等原因，整流器本身不可能完全工作在单位功率因数情况下。在非单位功率因数、大功率运行情况下，整流器若采用传统的CB- PWM，会产生违背正常运行前提的区域。如图4中的区域A所示，该区域主要由两部分组成：①此时输入电流易受干扰，输入侧电感上的压降不能忽略，故电网电压E和整流器交流侧输入电压Vref存在相位差z；②随功率因数的超前或滞后，网侧电流零点相应前后移动，产生功率因数偏移角pf。这时，将会引起大量的谐波干扰。因此，需要先量化z与pf，即量化区域A，再设计相应的补偿措施。

图4 电压电流相位关系图

步骤1：有关阻抗偏移角z的求解。交流侧局部电路等效结构如图5所示。这里只考虑滤波器的阻抗。

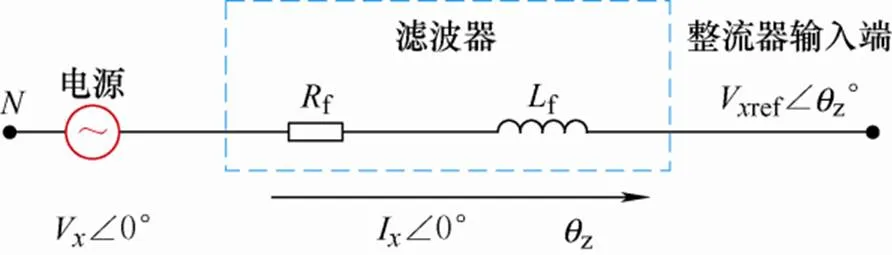
图5 交流侧局部电路等效图

分析图5的电路原理，有

式中，f、f分别为滤波器的等效电阻和电感。

将式(7)整理成如下形式

进而，可得阻抗偏移角z的计算式

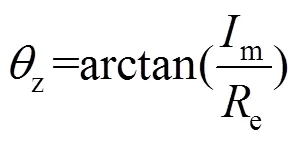
其中实部e和虚部m表达式为

步骤2：有关功率因数偏移角pf的求解。由相关原理知其计算公式如下

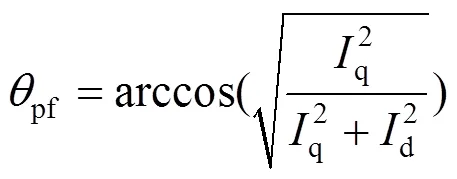
步骤3：有关补偿策略的提出。本文暂且忽略阻抗角z的影响，仅考虑电网电压与三相输入电流的相位差，即设置在滞后功率因数情况下，此时区域A=pf。为降低过零点处输入电流总谐波畸变率(Total harmonic distortion, THD)，本文在电流过零点附近出现的区域(电压电流极性相反的区域)内，将三相参考调制电压aref, offset、bref, offset、cref, offset置零，因此需要在一个工频周期出现的多个“区域A”对应增加恰当的补偿调制电压。补偿策略的数学表达式如式(12)所示

三相电流出现的六个过零点补偿区域如图6所示。经分析，六个补偿区域对应的补偿分量Vcomp如表1所示。

表1 补偿角度范围及补偿电压Vcomp

4 Vienna整流器整体控制框图

三相Vienna整流器采用MCB-PWM的基础上，结合传统PI双闭环形成系统整体控制框图如图7所示。电压外环的主要作用是控制整流器直流侧电压稳定，电流内环的主要作用是按外环输出的指令进行电流控制。

图7 整体控制框图

为实现单位功率因数运行，设置轴电流参考值q*=0。将电压外环比例、积分系数分别设置为KP=0.5、KI=5；电流内环比例、积分系数分别设置为KP=0.3、KI=8。

5 仿真分析及验证

为验证本文所提策略的正确性，根据系统整体控制框图，在Matlab/Simulink仿真系统中搭建仿真模型，对比调制策略改进前后输入电流畸变情况。仿真参数如表2所示。

表2 仿真参数

在旋转坐标系下的Vienna整流器数学模型及常规双闭环PI控制下，进行负载突变试验。设置系统直流侧输出电压给定值dc*=200 V，在=0.5 s时，负载由50 Ω突变为25 Ω，得到整流器负载突变仿真波形如图8所示。负载突增时，系统输出电压dc大约需要4个工频周期的调节时间过渡并稳定到给定值200 V；负载突增时，A相输入电流a经过短暂的调节时间能过渡到新稳态，且电流正弦度良好，轴输入电流d能过渡到新的期望值并保持稳定，轴输入电流q在负载突变后仍能保持在零值附近；在不同负载稳定运行过程中，电网电压a与输入电流a几乎保持同相位，实现了高功率因数运行。综上表明，本文所提三相Vienna整流器系统稳态、动态特性良好。

图8 负载突增时直流侧电压及A相输入电流动态波形

在整流器控制稳定的前提下，分别采用传统CB-PWM策略及本文所采用的增加补偿分量后的MCB-PWM策略所对应的三相调制电压波形，如图9所示。由图9可见，增加补偿分量后，调制波在相应过零点区间保持零值，验证了本文按照表1所添加补偿电压值的正确性。如图9b中虚线框区域即是B相调制波某一置零区域，这些区域可使整流器因开关器件等因素导致非单位功率因数运行时产生的过零点畸变问题得以解决，消除电压电流极性不一致的区域，最终保证整流器的正常运行。

图9 补偿前后调制波波形

为直观反映本文所提MCB-PWM算法的正确性及改善电流过零点畸变的有效性，设置两组参数进行验证，即dc=200 V、load=50 Ω；dc=250 V、load=50 Ω。分别在两组参数下将MCB-PWM策略与传统CB-PWM策略进行比较，仿真结果如图10、11所示。

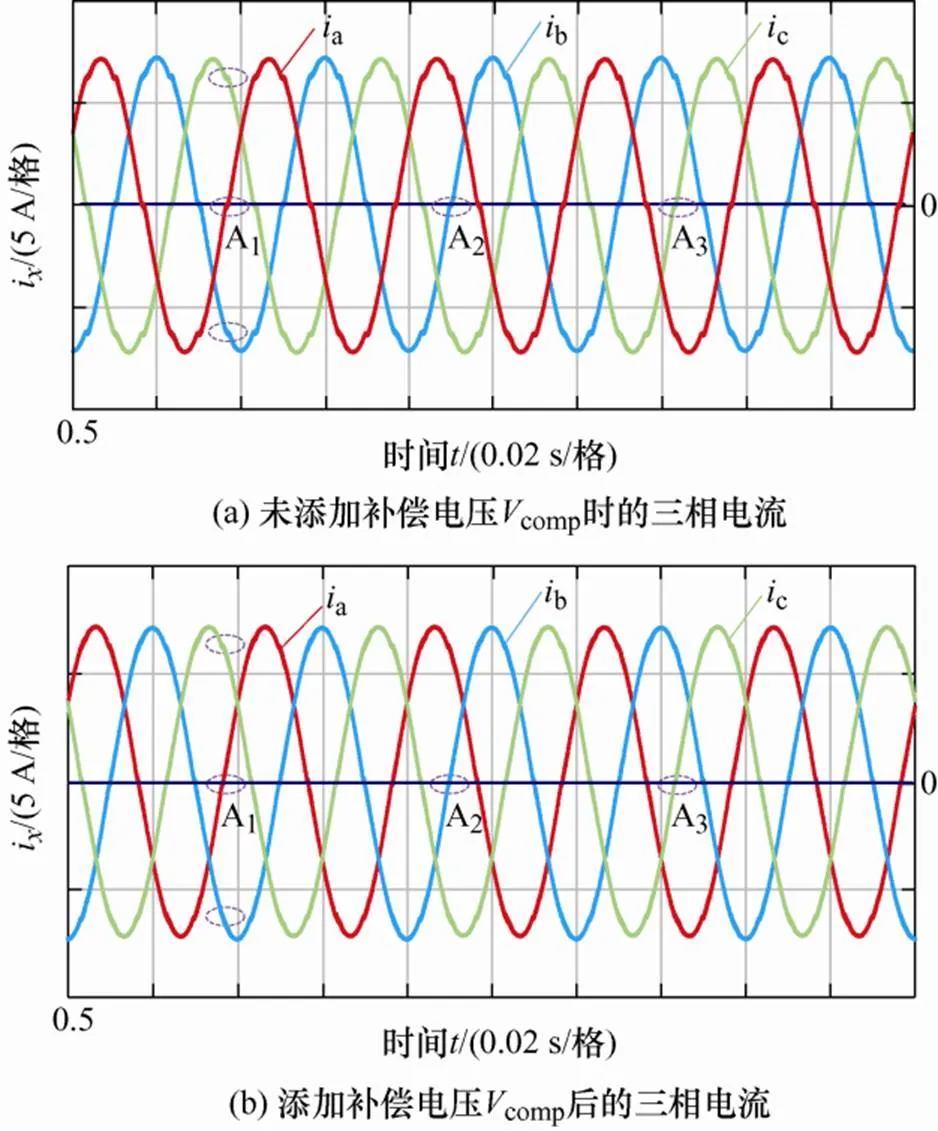
图10 Udc=200 V，补偿前后三相电流波形

图10、11中区域A1、A2、A3分别代表A、B、C三相电流a、b、c的某一过零点区域。由图10a、11a可见，传统CB-PWM策略所得的三相输入电流在过零点处均出现畸变现象，这是由于单位功率因数下，未添加补偿电压comp时，电源与整流器网侧电压存在相位差，从而产生了电压电流极性不一致的区域。由图10b、11b可见，按照表1添加补偿电压comp后，三相电流在过零点处的畸变程度得到减轻，电流波形的平滑性得到了显著提升，验证了本文所提调制策略的正确性。

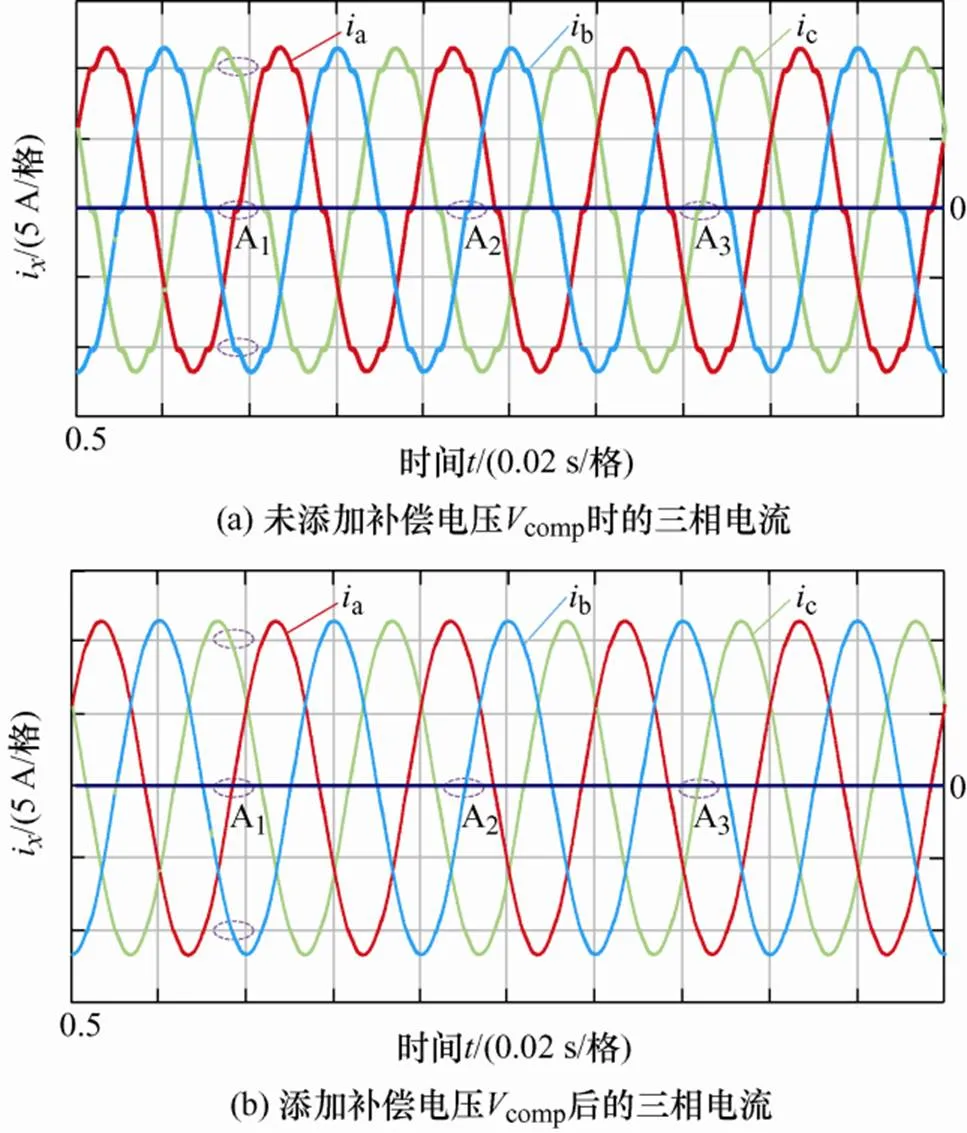
图11 Udc=250 V，有无补偿电压时三相电流波形

6 结论

本文通过对Vienna整流器工作原理的分析，建立了坐标系下的数学模型。针对整流器处于非单位功率因数运行状态下，运用传统基于载波的脉宽调制策略(CB-PWM)时三相电流过零点处畸变率高的问题，提出添加补偿电压分量加以改善，并经理论分析、推导、计算出了补偿角度区间及相应的补偿电压值。仿真结果表明，本文所提MCB-PWM策略具有以下优势。

(1) 能有效改善三相输入电流过零点处波形的平滑性，进而降低电流总谐波畸变率。

(2) 算法简单且易于衍生至其他Vienna型整流器拓扑结构。

[1] 范必双，谭冠政，樊绍胜，等. 一种具有双非零电压矢量输出的三电平PWM整流器直接功率控制方法[J]. 中国电机工程学报，2015，35(22)：5832-5841.

FAN Bishuang，TAN Guanzheng，FAN Shaosheng，et al. A direct power control method for three-level PWM rectifier with output of double non-zero voltage vectors[J]. Proceedings of the CSEE，2015，35(22)：5832-5841.

[2] 曹晓冬，谭国俊，王从刚，等. 三电平PWM整流器多模型预测控制方法[J]. 电工技术学报，2014，29(8)：142-150.

CAO Xiaodong，TAN Guojun，WANG Conggang，et al. Research on multi-model predictive control strategy of three-level PWM rectifier[J]. Transactions of China Electrotechnical Society，2014，29(8)：142-150.

[3] 谭国俊，曹晓冬，王从刚，等. 基于满意优化的三电平PWM整流器瞬时开关频率抑制方法[J]. 中国电机工程学报，2014，34(24)：4057-4067.

TAN Guojun，CAO Xiaodong，WANG Conggang，et al. Instantaneous switching frequency suppression method for three-level PWM rectifier based on satisfactory optimization[J]. Proceedings of the CSEE，2014，34(24)：4057-4067.

[4] ZHU W，CHEN C，DUAN S，et al. A carrier-based discontinuous PWM method with varying clamped area for Vienna rectifier[J]. IEEE Transactions on Industrial Electronics，2019，66(9)：7177-7188.

[5] 郝振洋，徐子梁，陈宇，等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报，2020，35(24)：5152-5163.

HAO Zhenyang，XU Ziliang，CHEN Yu，et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electrotechnical Society，2020，35(24)：5152-5163.

[6] PARK J H，LEE J S，LEE K B. Sinusoidal harmonic voltage injection PWM method for Vienna rectifier with an LCL filter[J]. IEEE Transactions on Power Electronics，2021，36(3)：2875-2888.

[7] 邹宇航，张犁，赵瑞，等. 三相Vienna整流器的不连续空间矢量脉宽调制及电压谐波分析方法[J]. 中国电机工程学报，2020，40(24)：8123-8130，8249.

ZOU Yuhang，ZHANG Li，ZHAO Rui，et al. Discontinuous pulse width modulation and voltage harmonic analysis method for three-phase Vienna-type rectifiers[J]. Proceedings of the CSEE，2020，40(24)：8123-8130，8249.

[8] BURGOS R，LAI Rixin，BOROYERICH D，et al. Space vector modulator for Vienna-type rectifiers based on the equivalence between two-and-three-level converters：A carrier-based implementation[J]. IEEE Transaction on Power Electronics，2008，23(4)：1888-1899．

[9] 姜海鹏，刘永强. 带中点电位平衡控制的VIENNA 整流器简化 SVPWM双闭环控制[J]. 电机与控制学报，2014，18(2)：35-41.

JIANG Haipeng，LIU Yongqiang. VIENNA rectifier with neutral potential balance control simplifies SVPWM double closed-loop control[J]. Journal of Electrical Machinery and Control，2014，18(2)：35-41.

[10] HANG L，LI B. Equivalence of SVM and carrier based PWM in three-phase/wire/level Vienna rectifier and capability of unbalanced-load control[J]. IEEE Transactions on Industrial Electronics，2014，61(1)：20-29.

[11] BURGOS R，LAI R，ROSADO S，at al. A full frequency range average model for Vienna-type rectifiers[J]. IEEE Transactions on Power Electronics，2009，24(11)：2509-2522.

[12] LEE J S，LEE K B. A novel carrier-based PWM method for Vienna rectifier with a variable power factor[J]. IEEE Transactions on Industrial Electronics，2016，63(1)：3-12.

[13] LEE J S，LEE K B. Carrier-based discontinuous PWM method for Vienna rectifiers[J]. IEEE Transactions on Power Electronics，2017，30(6)，2896-2900.

[14] 杨頔，姚钢，周荔丹. 功率变化环境下的四线制Vienna整流器优化联合控制方法[J]. 电工技术学报，2021，36(2)：305-319.

YANG Di，YAO Gang，ZHOU Lidan. An improved control method of 4-wire Vienna rectifier considering power fluctuation[J]. Transactions of China Electrotechnical Society，2021，36(2)：305-319.

[15] 王涛，陈昌松，段善旭，等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报，2019，34(18)：3854-3864.

WANG Tao，CHEN Changsong，DUAN Shanxu，et al. An improved space-vector modulation for Vienna rectifier to eliminating current distortion around zero-crossing point[J]. Transactions of China Electrotechnical Society，2019，34(18)：3854-3864.

[16] ZHANG B，ZHANG C，XING X，et al. Novel three-layer discontinuous PWM method for mitigating resonant current and zero-crossing distortion in Vienna rectifier with an LCL filter[J]. IEEE Transactions on Power Electronics，2021，36(12)：14478-14490.

[17] WU F，LI X，DUAN J. Improved elimination scheme of current zero-crossing distortion in unipolar hysteresis current controlled grid-connected inverter[J]. IEEE Transactions on Industrial Informatics，2015，11(5)：1111-1118.

[18] YIN H，LANG T，LI X，et al. A hybrid boundary conduction modulation for a single-phase H-bridge inverter to alleviate zero-crossing distortion and enable reactive power capability[[J]. IEEE Transactions on Power Electronics，2020，35(8)：8311-8323.

[19] 王楠，易映萍，张超. 微逆变器过零点电流畸变抑制的混合控制策略[J]. 电力系统保护与控制，2014，42(20)：59-63.

WANG Nan，YI Yingping，ZHANG Chao. Hybrid control strategy for suppressing zero-crossing current distortion of micro-inverter[J]. Power System Protection and Control，2014，42(20)：59-63.

[20] 刘斌，粟梅，林小峰，等. 非隔离型H6桥单相光伏逆变器无功补偿调制及并网电流波形改善控制[J]. 中国电机工程学报，2016，36(4)：1050-1060.

LIU Bin，LI Mei，LIN Xiaofeng，et al. Reactive power compensation modulation and waveform-improving control strategy for non-isolated H6-type single-phase photovoltaic grid-connected inverter[J]. Proceedings of the CSEE，2016，36(4)：1050-1060.

[21] 杨明，刘杰，梁轩瑞，等. 一种有源功率因数校正电流畸变抑制控制技术[J]. 电力系统自动化，2014，38(3)：30-35.

YANG Ming，LIU Jie，LIANG Xuanrui，et al. A control strategy of boost PFC to minimize current zero-crossing distortion[J]. Automation of Electric Power System，2014，38(3)：30-35.

Modified Carrier-based Pulse Width Modulation Strategy for Three-phase Vienna Rectifier

CHEN Lan1, 2XIAO Huihui1, 2GUO Qiang1, 2XIANG Wenkai1, 2

(1. School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054;2. Chongqing Energy Internet Engineering Technology Research Center, Chongqing 400054)

Considering the influence factors such as filter inductance, parasitic parameters of switching devices and control delay, so the rectifier may work in the state of non-unity power factor. At this time, if the rectifier adopts the traditional carrier-based pulse width modulation (CB-PWM) strategy, an area with inconsistent voltage and current polarity will be generated, which may cause the switching tubes to malfunction and the performance of the rectifier to decrease. For this reason, a modified carrier-based pulse width modulation strategy (MCB-PWM) is proposed based on the traditional CB-PWM strategy to improve the zero-crossing distortion of the rectifier. First, based on the working principle of the three-phase Vienna rectifier, a mathematical model is established in a two-phase rotating (-) coordinate system; secondly, the causes of waveform distortion at the grid-side current zero-crossing point caused by the traditional CB-PWM strategy is analyzed in detail, the compensation measure is designed, and the specific principle of the MCB-PWM strategy is given; in addition, the overall control block diagram of the system is formed by combining the traditional double closed-loop control; finally, the traditional CB-PWM strategy is compared with the MCB-PWM strategy by the simulation in Matlab/Simulink. The results show that the input current zero-crossing distortion phenomenon can be significantly improved by using the MCB-PWM strategy, and the correctness and effectiveness of the theoretical analysis are verified.

Vienna rectifier；zero-crossing distortion；CB-PWM；Simulink simulation

10.11985/2021.04.018

TM461

* 重庆市教委科学技术研究(KJQN202001128)和重庆理工大学研究生创新重点(clgycx20201004)资助项目。

20210908收到初稿，20211112收到修改稿

陈岚，女，1998年生，硕士研究生。主要研究方向为大功率整流器及控制技术等。E-mail：1335083504@qq.com

肖蕙蕙，女，1964年生，博士，教授。主要研究方向为电力电子传动、新能源发电与控制等。E-mail：xhh@cqut.edu.cn

郭强(通信作者)，男，1984年生，博士，讲师。主要研究方向为大功率整流器、改进逆变器、汽车电子等。E-mail：guoqiang@cqut.edu.cn

向文凯，男，1996年生，硕士研究生。主要研究方向为大功率整流器及控制技术等。E-mail：1334967843@qq.com