青藏高原东北缘地震波衰减特征及地震震源参数研究

臧 阳 俞言祥 孟令媛 韩颜颜

1）中国地震局地球物理研究所，北京 100081

2）中国地震台网中心，北京 100045

0 引言

青藏高原东北缘（31.9°～36.4°N，98.8°～105.6°E）位于南北地震带中北段附近，历史地震活跃，曾发生1933年四川迭溪7.5级、1947年青海达日7.7级、1976年四川松潘－平武2次7.2级、1990年青海共和7.0级、2013年甘肃岷县－漳县6.6级以及2017年四川九寨沟7.0级地震。区域发育多条活动断裂，以NWW 走向断裂为主，如自北向南展布的西秦岭北缘断裂、临潭－宕昌断裂、东昆仑断裂等，以及近SN向的日月山断裂、岷江断裂等。其中东昆仑断裂东侧玛沁—玛曲段存在地震空区（Wenetal．，2007），强震危险性尤为突出，2017年九寨沟7.0级地震的发生不仅没有缓解该地区强震危险，还导致东昆仑断裂带东端累计库仑应力的增加（徐晶等，2017），增强了青藏高原东北缘的强震紧迫性。

地震活动与区域应力场变化及地下介质状态密切相关。利用宽频带数字地震台网，可从中小地震的三分量地震信号中提取震源参数、地震波衰减特征以及场地响应等相关信息。可获取的震源参数包括地震矩、应力降、震源破裂尺度等，能够定量描述区域应力环境并反映研究区地震震源的普遍特征。地震波衰减又分为几何扩散衰减以及常使用品质因子Q值描述的介质非弹性衰减，反映了研究区地下介质的物理性质和状态。场地响应同样是控制地震破坏的重要因素之一，尤其对于非基岩场地可产生明显的场地放大效应。

本文基于青藏高原东北缘2010—2019年中小地震宽频带三分量记录，采用联合反演方法（Atkinsonetal．，1992；黄玉龙等，2003；刘杰等，2003）获取了该地区的地震波衰减特征和地震震源参数，分别给出了研究区几何衰减模型、区域Q值和118个台站的场地响应结果，分析了区域444次地震应力降、视应力随矩震级的分布特征。该结果可为青藏高原东北缘地区地震动模型的建立、地震灾害评估等提供研究基础。

1 数据选取与处理

研究使用的地震波形数据来自中国地震局地球物理研究所“国家数字测震台网数据备份中心”(1)http：∥www．seisdmc．ac．cn／。（郑秀芬等，2009），包括2010—2019年研究区及邻区127个台站记录到的452次地震事件，共计33 090条记录，所选地震的震级范围为ML3.0～5.9。以震中距300km为最大阈值，按每个地震至少被5个台站记录到、每个台站至少记录到5次地震为筛选条件，最终挑选了由118个台站记录到的具有高信噪比的444次地震事件，共计33 006条记录参与后续的反演计算（图1）。筛选后的地震和台站较均匀地分布于研究区及其附近，地震射线路径覆盖区与研究区范围基本一致，最终的反演结果能够反映青藏高原东北缘介质、震源的普遍特征。

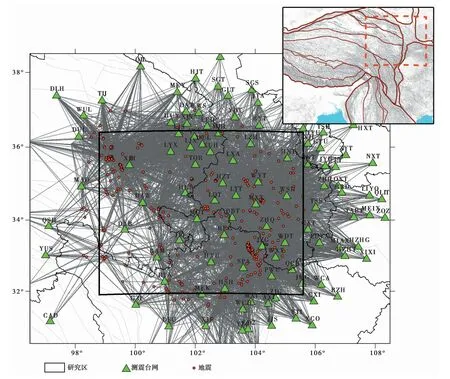
图1 参与反演计算的地震、台站和射线路径分布图Fig．1 Earthquakes，seismic stations and ray paths distribution involved in the inversion calculation．

近震记录中的S波能量较强，截取包含90%S波能量的E、N二水平分量地震信号分别进行去均值、去线性趋势以及0.5～25Hz二阶带通滤波，去除仪器响应后，经过地震波水平分量旋转获取径向R和切向T分量地震波，将T分量的S波作为输入数据。在频率域进行反演计算，需将原始地震仪速度记录转换为频率域加速度谱振幅并进行平滑处理。计算方法采用平移窗谱法（Chael，1987），使用长度为256个采样点、有50%部分重叠的平移窗对S波信号进行分段，对于100Hz采样频率的数据，每段为2.56s，共分为n段，对每小段原始速度信号进行两端尖灭处理后再做傅里叶变换，通过差值得到采样频率为10－0.3、10－0.25、10－0.2、…、101.25、101.3共33个频率采样点的速度谱振幅，按式（1）计算S波的加速度谱振幅：

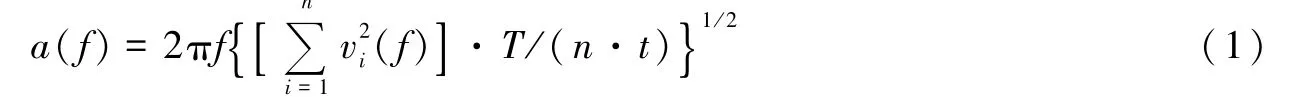
式中，vi（f）为第i个平移窗内信号傅里叶速度谱振幅，T为S波信号总持时，t为平移窗持时，这里为2.56s。对式（1）两端除以2πf和（2πf）2，可分别获取平滑后的S波速度谱和位移谱。以随机选取的2011年2月24日5时11分发生在青海兴海县的ML4.1地震为例，图2a—e为随机选取的地震周边不同震中距的5个台站记录到的S波T分量记录和去噪声后的观测位移谱，其中红色实线为利用平移窗谱法计算得到的位移谱。与实际观测位移谱相比，经平滑后的计算结果能够反映真实位移谱随频率的变化形态。

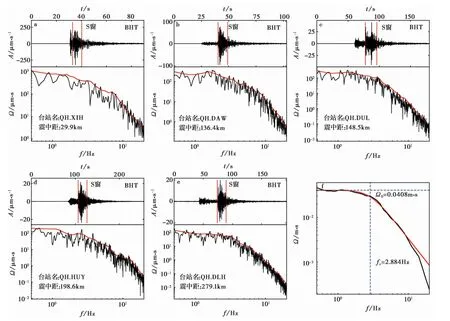
图2 不同台站记录到的2011年2月24日青海兴海M L 4.1地震T分量S波记录、去噪声后的观测位移谱及联合反演得到的地震震源位移谱Fig．2 The T component S wave records，observed noise removed displacement spectra of the M L 4．1 Xinghai earthquake on February 24，2011 recorded by different stations and the source displacement spectra obtained by joint inversion．a青海兴海台（QH．XIH）S波T分量记录及观测位移谱；b青海大武台（QH．DAW）S波T分量记录及观测位移谱；c青海都兰台（QH．DUL）S波T分量记录及观测位移谱；d青海湟源台（QH．HUY）S波T分量记录及观测位移谱；e青海德令哈台 （QH．DLH）S波T分量记录及观测位移谱；f联合反演得到的青海兴海M L 4.1地震的震源位移谱

2 计算方法

2.1 地震波衰减及场地响应计算

去除仪器响应后，地震波观测信号在频率域下可用式（2）表示（Hartzell，1992）：

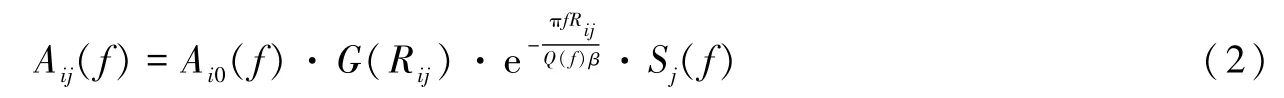
式中，Aij（f）为第j个台站记录到的第i个地震的S波加速度谱振幅，Ai0（f）为第i个地震震源加速度谱，Rij为震源距，G（Rij）为几何扩散函数，Q（f）为品质因子，β为S波速度，本文取β＝3.5km／s，Sj（f）为第j个台站的场地响应。进一步由式（2）可得到：

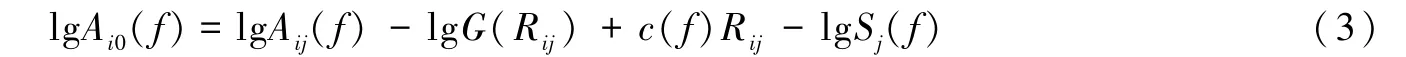
其中，

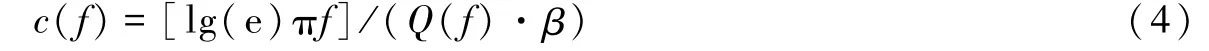
式中，c（f）称为非弹性衰减系数，确定c（f）后即可计算Q（f）值。分别考虑地震波在全空间和半空间中传播，几何衰减模型分别为G（Rij）＝R－b1ij和由式（5）确定的二段几何衰减函数：

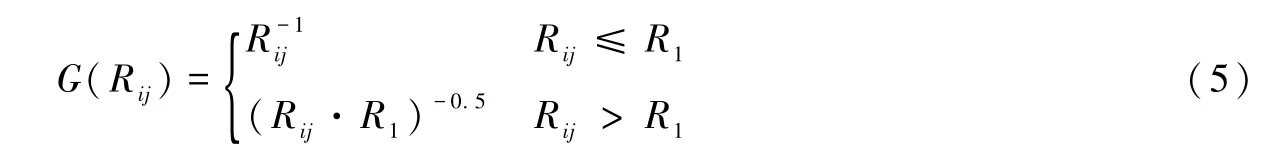
其中，R1的取值与区域地壳厚度相关，一般取地壳厚度的1.5倍。地震波实际衰减特征则更为复杂，如当直达波与莫霍面及地壳内间断面的过临界反射波叠加时，在一定震中距范围内，地震波振幅并不会随着距离的增加而减小，这个震中距范围大约在1.5～2.5倍地壳厚度之间，此时几何衰减大致满足三段式分段函数形式，如Atkinson等（1992）采用三段式分段函数描述了加拿大东南部地震波几何衰减特征：

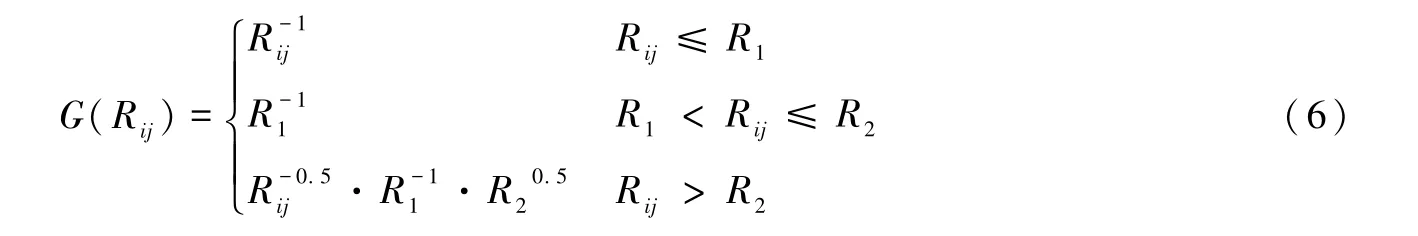
由CRUST1.0模型得到研究区的平均地壳厚度为56km，可由此确定初始G（Rij）。初始场地假设为基岩（lgSj（f）＝0），开始迭代计算。对于任一地震而言，不同台站记录到的地震震源谱应相同，定义δij为第j个台站记录到的第i个地震的震源谱与所有台站记录到的第i个地震震源谱均值的残差，即

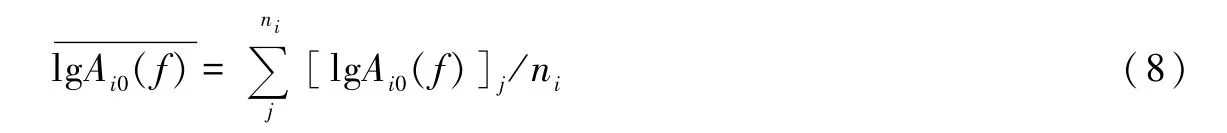
其中，ni为记录第i个地震的台站个数。进一步定义总残差δ为

由式（3）可知，在已知几何衰减函数G（Rij）和场地响应Sj（f）的情况下，通过调整非弹性衰减系数c（f）使得总残差δ最小，可确定c（f）。进一步调整几何衰减项参数R1，使总残差δ进一步减小。利用式（10）对第j个台站的场地响应项进行修正：

其中，mj为第j个台站记录到的地震个数，将Δ［lgSj（f）］代入迭代起始位置反复计算，直到总残差δ不再减小，可最终确定G（Rij）、Sj（f）和c（f），进一步根据式（4）确定品质因子Q（f）。

2.2 震源参数计算

计算得到G（Rij）、Sj（f）和c（f），由式（8）计算第i个地震的平均理论震源加速度谱Ai0（f），震源理论位移谱Ω0（f）可表示为

图2 f中，黑色实线为计算得到的2011年2月24日青海兴海县ML4.1地震震源理论位移谱，该理论震源谱由符合条件的21个台站的观测位移谱联合反演得到。与图2a—e列举的各台站记录相比，理论位移谱更加平滑，且由于去除了传播路径的影响，理论位移谱相当于震中距为1km时台站的理论观测值，其谱能量高于各台站的实际记录结果。对于圆盘模型，理论震源位移谱可表示为（Brune，1970；Boatwright，1978）

式中，Ω0为零频极限，fc为拐角频率。对计算得到的理论位移谱Ωi0（f）按式（12）采用最小二乘法进行非线性拟合可确定第i个地震的Ω0和fc。图2 f中的红色实线为按式（12）拟合得到的曲线，与理论位移谱在形态上具有较高的相似度，计算得到的该地震的fc和Ω0分别为2.884Hz和0.040 8m·s。地震矩M0、震源半径R和应力降Δσ则可分别表示为

其中，ρ为地壳介质密度，取2.7g／cm3，Rθφ为辐射因子，对于S波可取0.63（Akietal．，2002）。

对速度谱的平方进行积分可得到地震能量ES，进一步计算视应力：

其中，μ为剪切模量，取值为3.0×104MPa。地震矩与矩震级MW之间满足经验关系（Hankset al．，1979）：

综上，可计算得到包括零频极限Ω0，拐角频率fc、地震矩M0、矩震级MW、震源破裂半径R、地震能量ES、应力降Δσ和视应力σapp的多项震源参数。

3 计算结果

3.1 地震波衰减特征

为方便分析区域的几何衰减特征，定义“归一化”振幅谱为（Atkinsonetal．，1992）

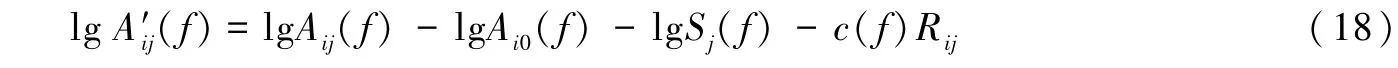
即从观测地震信号谱中扣除理论震源谱、场地响应以及非弹性衰减项，所得结果反映了地震波各频率成分的几何衰减特征。分别采用线性模型、二段式分段函数模型以及三段式分段函数模型考察拟合结果与实际归一化振幅谱的匹配程度。当频率取2.0Hz时，3种模型的拟合结果如图3所示，其中线性模型经迭代反演确定满足G（Rij）＝的参数b1为1.0；满足式（5）的二段式分段函数模型的参数R1＝91km；满足式（6）的三段式分段函数模型的参数R1＝115km，R2＝155km。

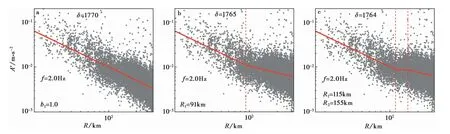
图3 几何衰减模型理论值及归一化振幅谱实测值Fig．3 Theoretical values of geometric attenuation model and measured values of normalized amp litude spectrum．a采用线性的几何衰减模型；b采用二段式分段函数的几何衰减模型；c采用三段式分段函数的几何衰减模型

基于3种不同模型反演得到的结果中，总残差δ显示在2.0Hz频率处三段式分段函数模型与二段式分段函数模型要略优于线性模型。其中，三段式分段函数模型的误差最小，且从归一化振幅谱实测点分布形态来看，在震中距115～155km范围内，相较于整体的衰减而言，归一化振幅谱在该震中距范围出现明显“平台阶段”，即更符合三段式分段函数的几何衰减模型假设。计算表明，在f≤2.0Hz低频区间三段式分段函数模型的误差一般最小，二段式分段函数模型其次，线性模型误差最大；在f＞9.0Hz的高频区间，结果则正好相反，线性模型的误差最小，二段式分段函数模型其次，三段式分段函数模型的误差最大；在2.0～9.0Hz范围内3种模型误差差异很小，这可能说明了相较于高频成分的地震波而言，低频地震波在莫霍面及地壳内间断面产生的过临界反射波能量更高。

在地震波非弹性衰减方面，描述其衰减特征的物理量Q值一般是关于频率f的函数，通常在双对数坐标系下Q值随f呈线性增长。分别采用3类几何衰减模型计算得到的Q值及拟合结果如图4所示，其中采用线性模型计算得到的Q值的低频成分计算结果不稳定，整个频率域范围在双对数坐标系下不满足线性分布。采用二段式、三段式分段函数模型能够得到较稳定的Q值，且在对数坐标系下与频率呈现出较好的线性分布特征，其中三段式分段函数模型更近似线性拟合结果，仅在f＜1Hz和f＞16Hz频率范围较拟合直线结果偏高，将该结果作为研究区内非弹性衰减模型，满足Q（f）＝401.8×f0．2963。

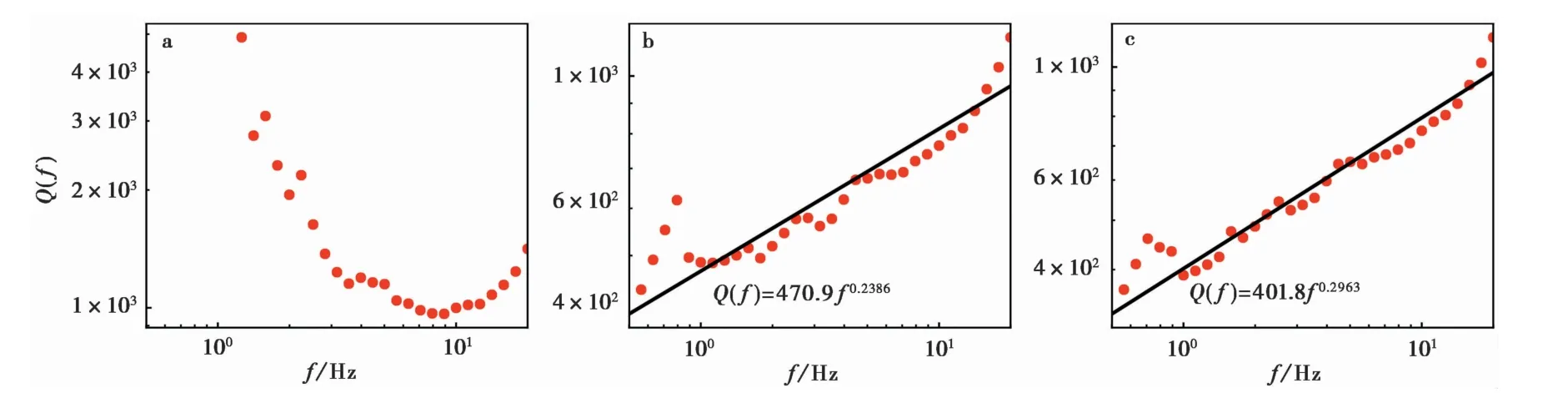
图4 Q值及对数坐标下的线性拟合计算结果Fig．4 Q value and the result of linear fitting in logarithmic coordinates．a采用线性的几何衰减模型；b采用二段式分段函数的几何衰减模型；c采用三段式分段函数的几何衰减模型

分别选取蒲举等（2019）针对甘东南地区、吴微微等（2016）针对四川盆地和川西高原地区、马建新等（2015）针对青海东南部地区、郭晓等（2008）针对甘肃地区以及陈继锋等（2010）针对甘东南地区的区域平均Q值反演结果进行对比（图5）。本研究的Q值计算结果与甘东南地区的2个结果极为相似，四川盆地和甘肃地区的Q值整体高于本文的计算结果，而青海东南部以及川西高原地区的Q值则整体偏低，仅在高频部分与本文结果相近。Q值的大小能够反映区域介质的破碎程度，地震波在构造相对稳定地区的传播过程中因散射造成的能量损耗较小，相应地具有较高的Q值。相反，在地下介质较为破碎的区域，地震波在传播过程中更易发生散射而损失能量，使得Q值较低。图5中，四川盆地和甘肃地区的Q值整体较高，反映这些区域的地壳整体上较为完整，而青海东南部和川西高原地区的Q值整体偏低，可能是区域介质破碎以及深部软流圈的物质流动造成的。由图1所示，研究区范围包含青海东南部、甘东南以及四川北部部分地区，Q值的反演结果反映了整个区域的平均值。甘东南位于研究区中心，地震射线覆盖最为密集，因此区域平均Q值反演结果在较大程度上受到甘东南地区介质破碎程度的影响。

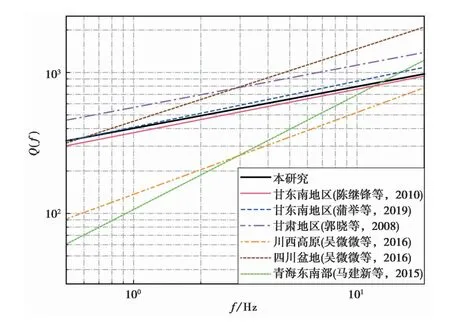
图5 各区域Q值随频率f变化的曲线对比图Fig．5 The comparison of the variation curve of Q with frequency f in different regions．

在反演计算过程中得到了研究区附近118个台站的场地响应S（f）。其中，88个台站的场地响应值在整个频率取值范围内均接近1，与基岩场地响应特征吻合，图6a列举了其中18个台站的场地响应反演结果。而青海台网化隆台（HUL）、李家峡台（LJX）、民和台（miH）、囊谦台（NAQ）、诺木洪台（NMH），陕西台网勉县台（miAX）、西乡台（XIXI）、太白台（TABT）、眉县台（MEIX）、略阳台（LUYA）、周至台（ZOZT），四川台网旺苍台（WCA）、峨眉山台（EMS）、荣县台（HMS）、井研台（JYA）、巴中台（BZH）、西充台（XCO）、平武台（PWU），甘肃台网会宁台（HNT），宁夏台网香山台（XSH）共20个台站反演得到的场地响应存在一定的放大效应（图6b），且多数台站（如民和台、勉县台、太白台、眉县台、略阳台、平武台、诺木洪台等）的放大效应主要表现在高频段，尤其在f＞5.0Hz的高频区间往往存在较为明显的高值。另外，青海台网大通台（DAT）、玛多台（MAD）、祁连台（QIL）、达日台（DAR）、曲麻莱台（QML）、清水河台（QSH），四川台网马尔康台（MEK）、理塘台（LTA）、雅江台（YJI），甘肃台网柳园台（LXA）共10个台站场地响应计算结果整体略＜1（图6c），可能是速度结构和Q值空间非均匀性的影响造成的计算误差。图7显示了具有不同场地响应特征的台站空间分布，其中具有一定场地放大效应的台站主要分布在研究区东南侧的四川盆地和其北侧陕西境内的小型盆地附近。场地响应整体略＜1的台站主要分布在海拔较高的川西高原和青海东南部地区。研究区内部的台站场地响应整体上符合基岩场地特征。

图6 反演得到的研究区不同台站的场地响应函数S（f）Fig．6 Site response function of different stations in the study area obtained by inversion．a具有典型基岩场地特征的场地响应；b具有一定放大效应的场地响应；c计算结果整体略＜1的场地响应

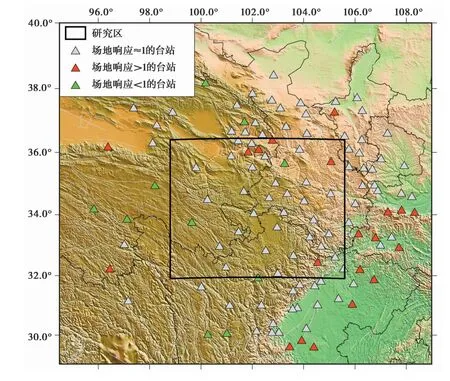
图7 具有不同场地响应特征的台站分布图Fig．7 Station distribution map with different site response characteristics．

3.2 震源参数反演

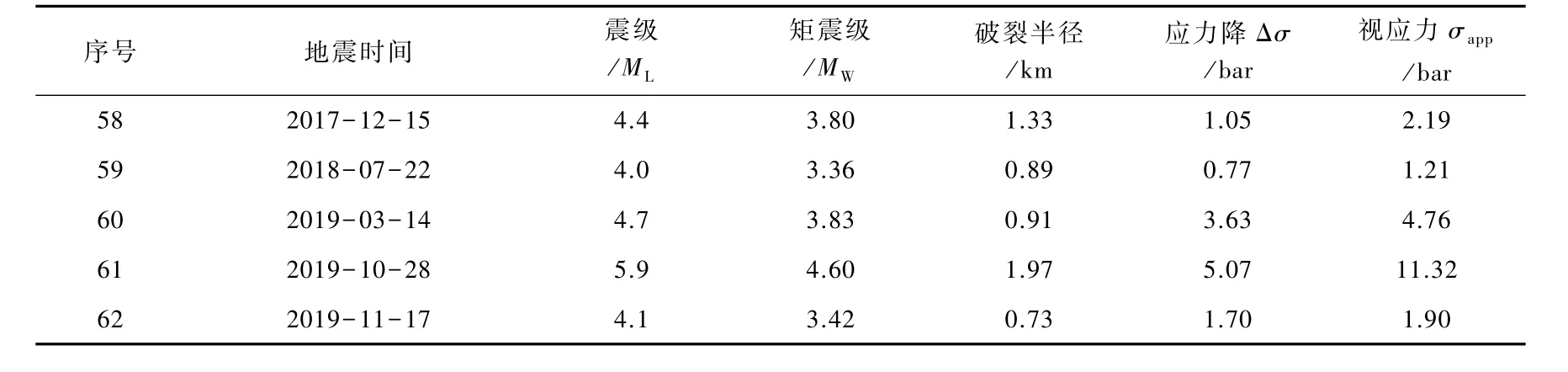
根据前文介绍的震源参数计算方法，得到了研究区内444次地震包括零频极限Ω0、拐角频率fc、地震矩M0、矩震级MW、震源破裂半径R、地震能量ES、应力降Δσ和视应力σapp等震源参数，其中ML≥4.0地震的部分震源参数计算结果列于表1。

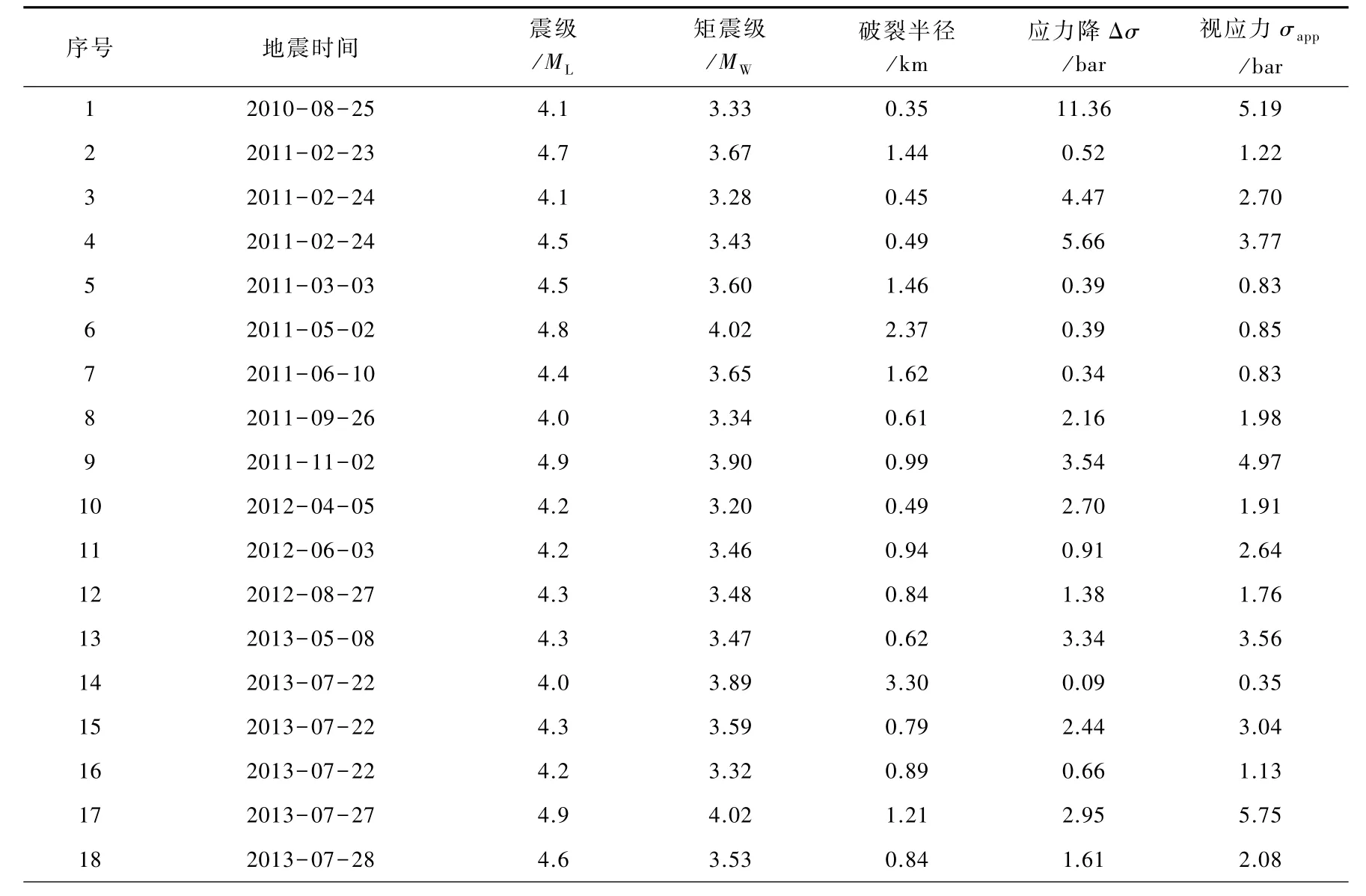
表1 M L≥4.0地震的震源参数反演结果Table 1 Seismic source parameters of M L≥4.0 events

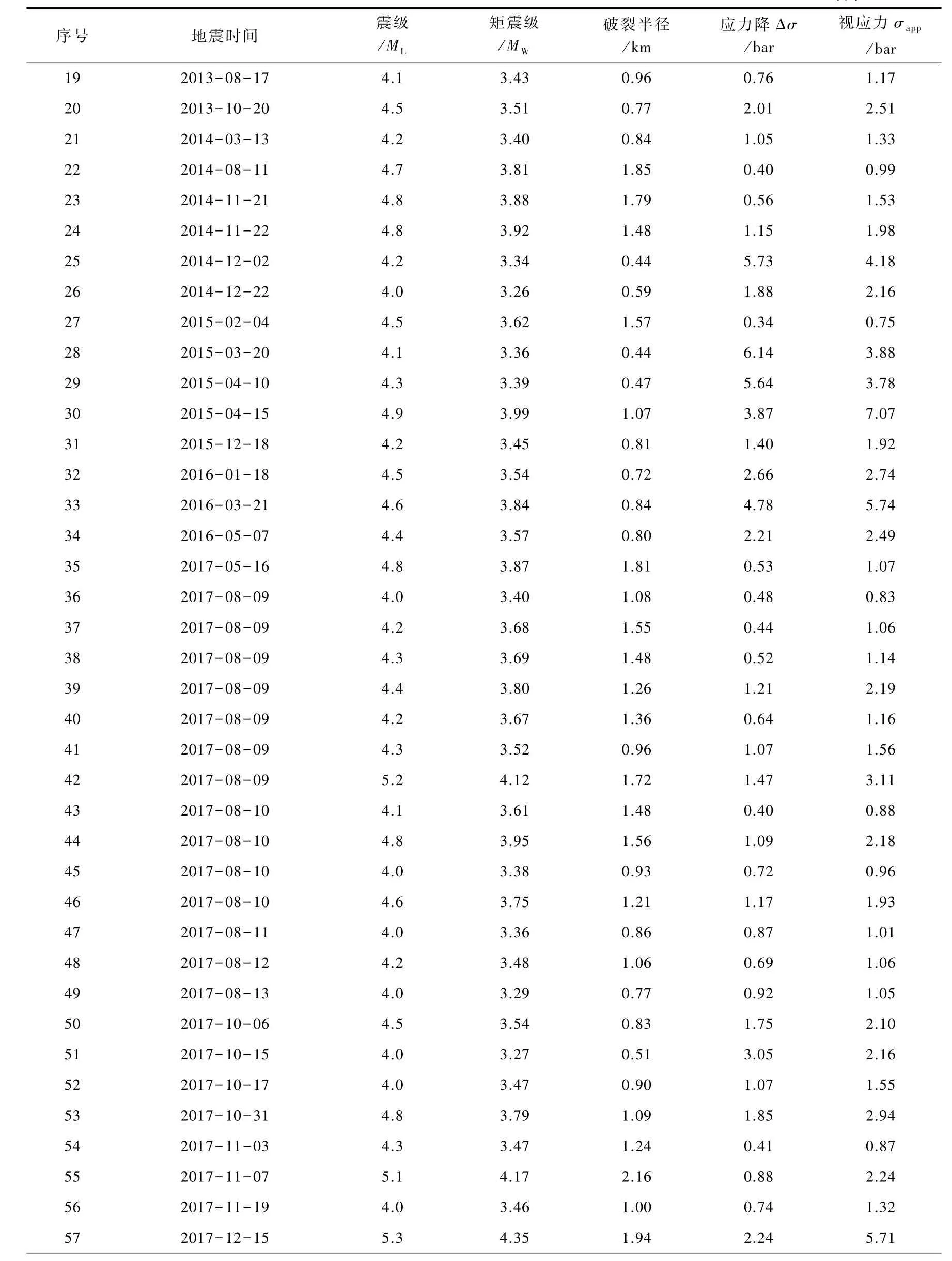
续表1

续表1

Δσ表征地震发生瞬间错动时位错面上的应力变化，中小地震的Δσ随时间的变化可能反映了区域应力状态的改变（华卫，2007）。σapp则表示单位面积上地震波辐射的能量，可作为区域绝对应力水平的间接估计。Δσ和σapp均可在一定程度上反映研究区背景应力水平，其随时间的变化与区域强震的发生可能存在一定联系（易桂喜等，2011，2013）。

地震的强度对Δσ和σapp可能存在一定影响，现有研究对Δσ和σapp与地震强度之间的关系尚存在较多争议。部分研究认为其与地震大小无关，如Abercrombie（1995）、Allmann等（2007）、Hardebeck等（2009）的研究表明ML1.0～3.0震级范围内地震的震级对Δσ和σapp基本没有影响；另有研究认为Δσ和σapp与地震矩之间存在一定关系（Mayedaetal．，1996；Moriet al．，2003；Tusaetal．，2008）；还有一些研究认为Δσ和σapp与地震震级的关系较为复杂，不同类型的地震具有不同特征（朱传镇等，1977；华卫等，2009；赵翠萍等，2011；周少辉等，

2017）。

本文尝试建立青藏高原东北缘地震Δσ和σapp与MW之间的统计关系。图8显示，Δσ随MW的变化整体较离散，随着MW的增加，Δσ未出现明显上升趋势。Δσ最大的地震为2010年8月25日青海兴海ML4.1地震，矩震级MW3.3，Δσ的反演结果为11.36bar。震级最大的地震，即2019年10月28日甘肃夏河ML5.9（MS5.7）地震，矩震级MW4.6，Δσ反演结果仅为5.07bar。使用最小二乘法分别对数据进行线性拟合和指数拟合，线性拟合的总残差为753.6，接近指数拟合的残差749.6，而基于数据平均值1.09bar的整体数据方差为771.0，三者差异较小，表明Δσ与MW的相关性不明显。

与Δσ相比，σapp与MW间存在较为明显的正相关（图8b），随着MW的增加，σapp整体呈现出明显上升趋势。MW最大的地震，即甘肃夏河MW4.6地震反演所得的σapp同样最大，为11.32bar。利用最小二乘法对数据进行线性拟合和指数拟合，残差分别为295.3和223.3，表明σapp随MW的增长更符合指数变化特征，指数拟合结果满足：

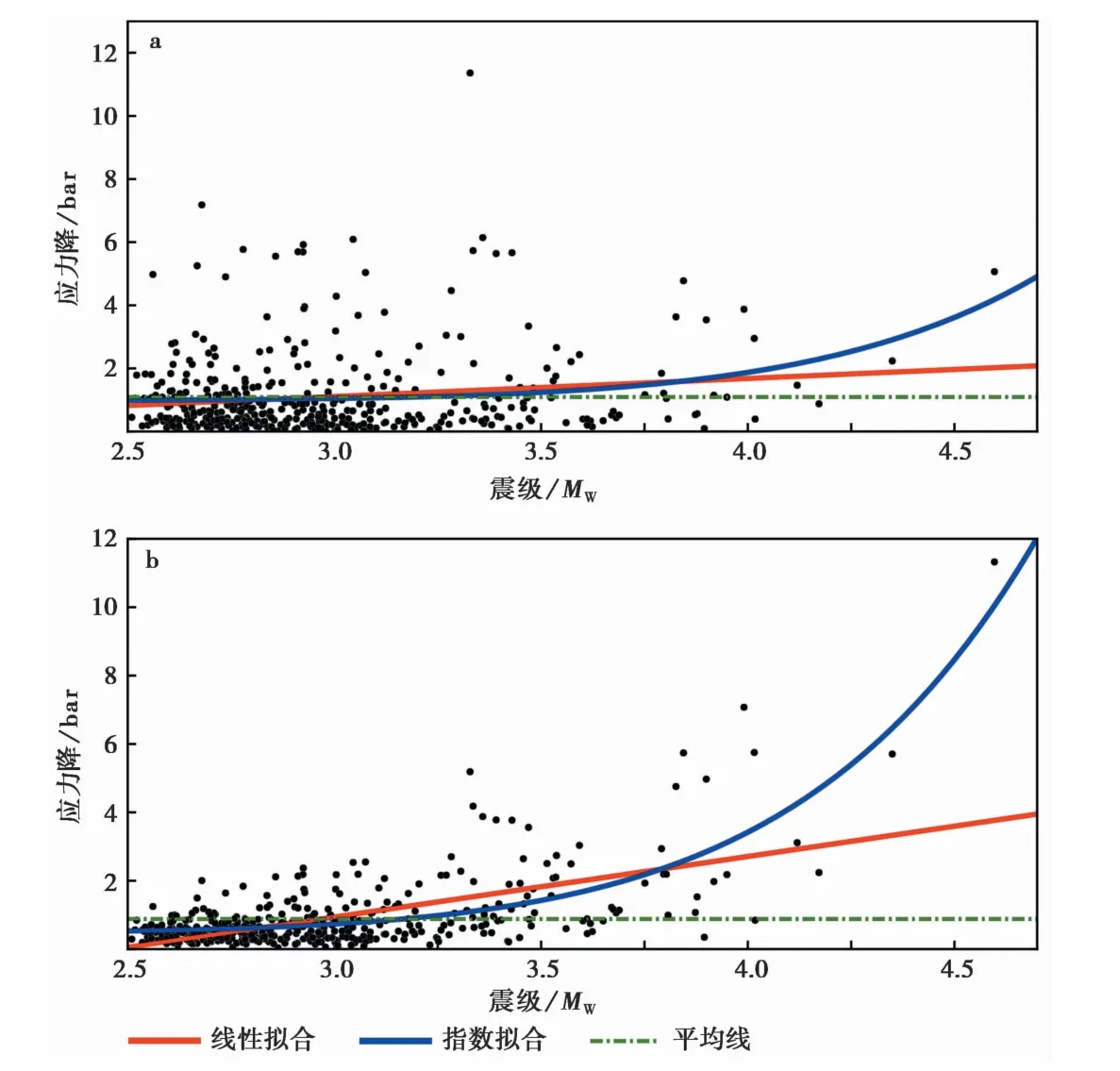
图8 M W 2.5～4.7地震的震源参数与地震矩震级相关性Fig．8 Correlation between seismic source parameters and momentmagnitudes in the range of M W 2.5～4.7．a应力降计算结果；b视应力计算结果

地方震级（ML）与MW间通常满足线性统计关系（Hanksetal．，1984；Thioetal．，1995；Bindietal．，2001；Rossetal．，2016）。从ML和MW的定义出发，结合震源物理相关方程，可推导ML满足（Deichmann，2006）：

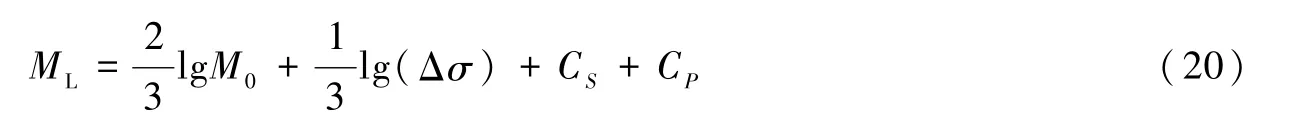
式中，CS为除Δσ外震源相关项，满足：

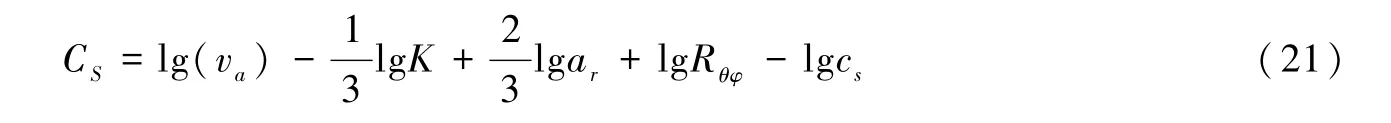
式中，va为断层视滑动速率；K为比例因子；ar为断层长宽比；cs为矩加速形态因子，反映了断层破裂的过程。式（20）中，CP为传播路径相关项，满足：

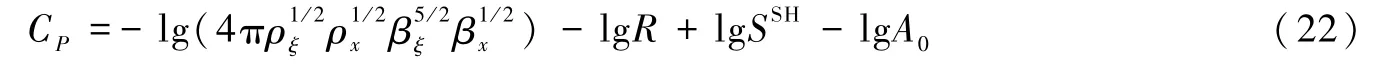
式中，ρξ、ρx分别为震源和台站处的介质密度，βξ、βx分别为震源和台站处的S波波速，R为震源距，SSH为自由表面放大系数，A0为ML定义中参考地震的地震波记录振幅，是关于震源距R的函数，满足：

式中，第1项表示地震波几何衰减，第2项表示非弹性衰减，第3项常数c2的作用为将地震波的振幅值转换为震级大小。通过对比式（20）和式（17）可知，在震源参数和传播路径相同的情况下，ML与MW仅相差1个常数，理论上二者比例应为1 1。然而由于震源参数、地震波非弹性衰减等因素的影响，实际观测到的结果往往显著偏离该理论值。对比研究区内ML震级范围在3.0～5.9的444次地震与MW的统计关系可知，ML和MW整体上满足线性相关关系（图9a），统计结果为

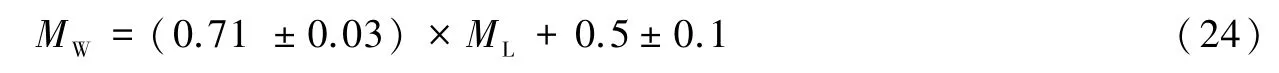
相关研究表明（Deichmann，2006，2017），式（20）中的传播路径项CP对ML的影响最为显著，是导致实际观测结果，即式（24）中ML前系数为0.71，而非理论值1的主要原因。式（21）所定义的CS中，cs、K、ar对ML在量级上的影响最小，而研究区内台站分布较为均匀，va和Rθφ造成的影响也可相互抵消，因此除Δσ外，其他震源参数对ML的影响可忽略不计。如图9a所示，将震级偏离拟合直线1倍、1.96倍（95%置信区间）标准差的地震用不同颜色标注，在Δσ随MW的变化曲线中（图9b），相同MW下ML偏高地震的Δσ同样偏高，整体高于对数平均值，ML偏低的地震的Δσ同样偏低，整体在对数平均线以下，该结果与由式（20）描述的Δσ与ML的函数关系相符，即在区域传播路径影响相对一致且CS可忽略不计的情况下，Δσ与ML呈正相关。σapp随MW的变化具有类似的统计规律（图9c），即σapp与ML同样呈正相关。尽管Δσ和σapp随MW的变化具有显著差异性，即随MW增大σapp呈趋势上升而Δσ变化不明显，但Δσ和σapp间仍存在较为显著的统计相关性，在对数坐标系下呈现出明显的线性相关性（图9d），该结果与Savage等（1971）以及Beeler等（2003）的研究具有一定的相似性。另外，如图9d所示，ML偏低的地震σapp／Δσ偏高，更接近应力上调模式，即地震破裂较为充分，地震波辐射能相对较小；ML偏高则σapp／Δσ偏低，断层破裂过程中损耗的能量相对较小，地震波辐射能相对较高。

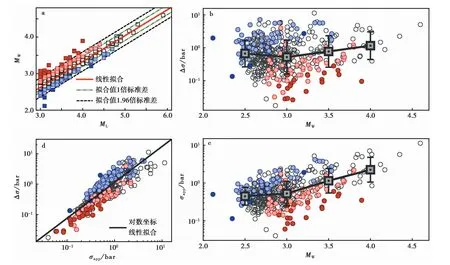
图9 地方震级（M L）、矩震级（M W）、应力降（Δσ）、视应力（σapp）的相关关系Fig．9 Correlation between localmagnitude（M L），momentmagnitude（M W），stress drop（Δσ）and apparent stress（σapp）．a地方震级与矩震级的相关性；b矩震级与应力降的相关性；c矩震级与视应力的相关性；d视应力与应力降的相关性。图a中黑色空心正方形为拟合值1倍标准差内的地震，浅红色正方形为拟合值加1～1.96倍均方差内的地震，深红色正方形为超过拟合值加1.96倍均方差的地震，浅蓝色正方形为拟合值减1～1.96倍均方差内的地震，深蓝色正方形为低于拟合值减1.96倍均方差的地震，图b、c、d中圆的颜色含义与图a一致；图b、c灰色方框为间隔0.5矩震级范围数据在对数坐标下的 平均值，误差棒为对数坐标下平均值的1倍均方差范围

4 结论和讨论

本文基于青藏高原东北缘2010—2019年中小地震的三分量S波数据，采用联合反演方法，获得了研究区地震波衰减特征、区内444次地震应力降Δσ、视应力σapp等震源参数以及118个台站的场地响应。研究表明，青藏高原东北缘的几何衰减符合三段式分段函数形式，在震中距115～155km范围内，地震波随震中距的增加衰减不明显，可能由于在该震中距范围内，直达波与莫霍面及地壳内间断面过临界反射波叠加导致。在该几何衰减模型的基础上，区域整体非弹性衰减模型满足Q（f）＝401.8×f0.2963，该结果与甘东南地区现有的Q值研究结果较为一致。在研究区内的118个台站中，94个台站场地响应值在整个频率取值范围内接近1，符合基岩场地响应特征，有20个台站的场地响应存在一定的放大效应，且多数台站的放大效应表现在高频区域，另有10个台站场地的响应计算结果整体略＜1，可能是受到了速度结构和Q值空间各项异性的影响。在反演的震源参数中，Δσ与MW的相关性不明显，σapp与MW间存在较为明显的正相关性，且σapp随MW的增长更符合指数变化特征。通过地方震级、矩震级、应力降和视应力的相关性研究，发现MW与ML整体呈线性相关，相同MW条件下ML偏高的地震的Δσ和σapp同样偏高，ML偏低的地震的Δσ和σapp同样偏低。Δσ和σapp间存在较为显著的统计相关性，在对数坐标系下呈明显线性相关关系。相同MW条件下ML偏低的地震σapp／Δσ偏高，更接近应力上调模式，即地震破裂较为充分，地震波辐射能相对较小；ML偏高的地震σapp／Δσ偏低，断层破裂过程中损耗的能量相对较小，地震波辐射能相对较高。